Graphing polynomials To graph a polynomial we need



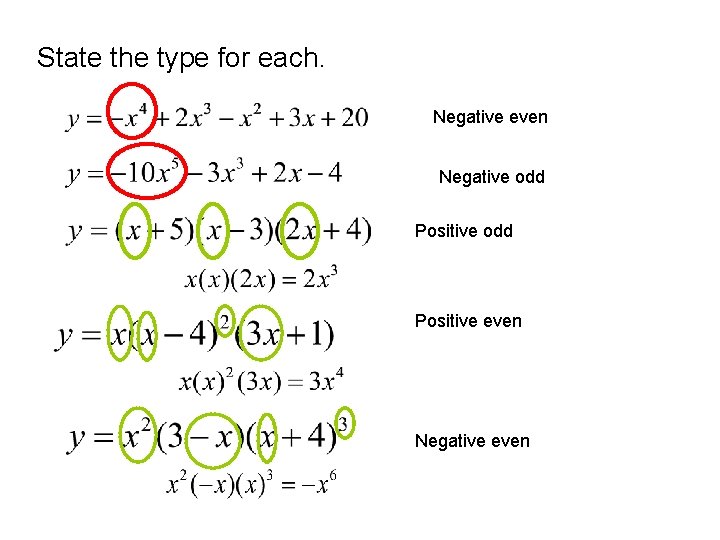








- Slides: 19

Graphing polynomials To graph a polynomial we need to know three things 1) Type of polynomial 2) Roots 3) y-intercept

Types of Polynomials Positive odd Negative odd Positive even Negative even Starts down ends up Starts up ends down Up on both ends Down on both ends

We can find the type from the sign and power of the leading term. The sign tells us if it is positive or negative and the power (degree) tells us if it is even or odd. Examples: The degree is even The coefficient is positive Type: positive even
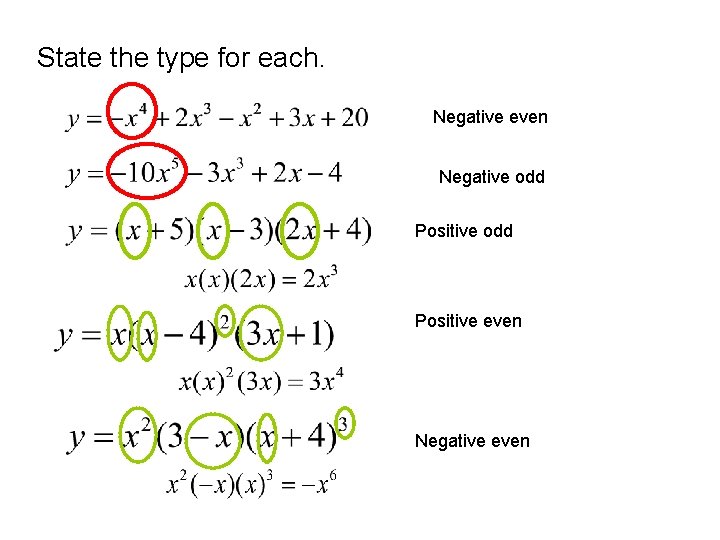
State the type for each. Negative even Negative odd Positive even Negative even

Roots The degree of the polynomial, tells us how many roots we will have. Example: How many roots will the following functions have? 4 roots 5 roots 4 roots 6 roots

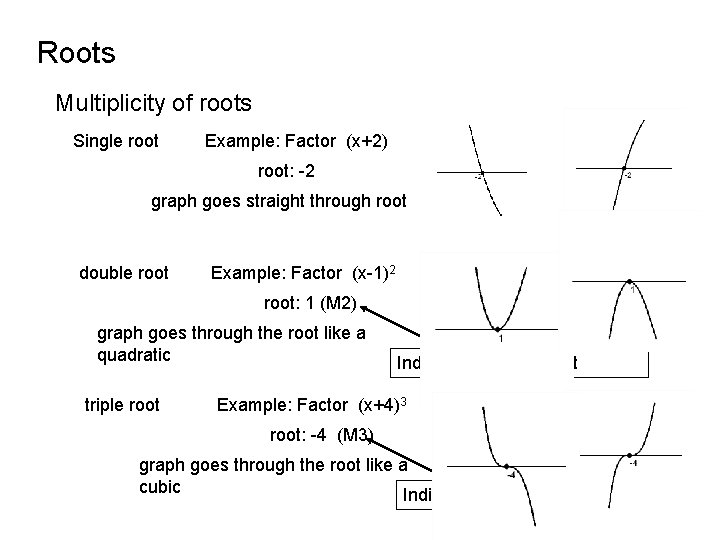
Roots Multiplicity of roots Single root Example: Factor (x+2) root: -2 graph goes straight through root double root Example: Factor (x-1)2 root: 1 (M 2) graph goes through the root like a quadratic triple root Indicates a double root Example: Factor (x+4)3 root: -4 (M 3) graph goes through the root like a cubic Indicates a triple root

Roots Real roots are x-intercepts. To find the roots, we let y = 0 and solve for x. Example: Find the roots for the following. Roots: -5, 3, -2 Roots: 0, 4 (M 2), Roots: 0 (M 2), 3, -4 (M 3)

Y-intercept To find the y-intercept let x = 0 Always write the y-intercept as a point. Example: Find the y-intercept for each y-intercept: (0, -60) y-intercept: (0, 20) y-intercept: (0, 0)

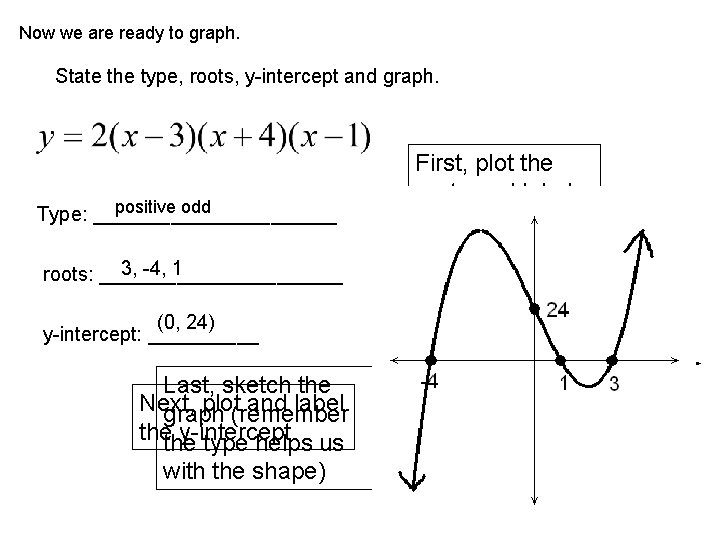
Now we are ready to graph. State the type, roots, y-intercept and graph. positive odd Type: ___________ 3, -4, 1 roots: ___________ (0, 24) y-intercept: _____ Last, sketch the Next, plot(remember and label graph thethe y-intercept type helps us with the shape) First, plot the roots and label

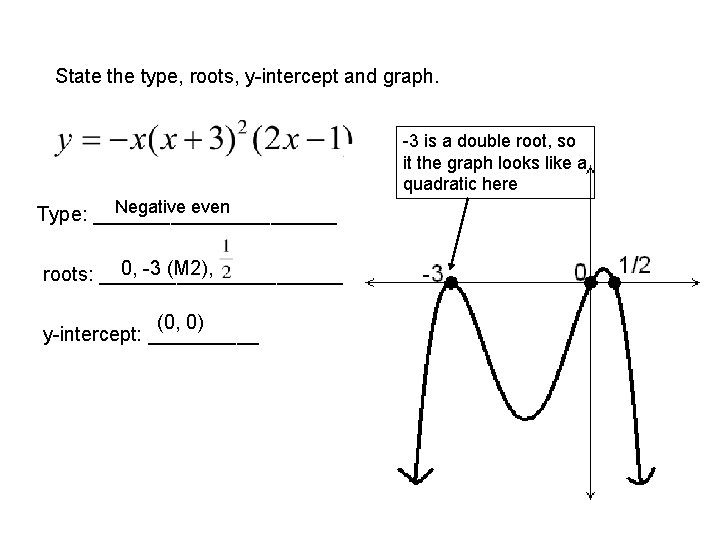
State the type, roots, y-intercept and graph. -3 is a double root, so it the graph looks like a quadratic here Negative even Type: ___________ 0, -3 (M 2), roots: ___________ (0, 0) y-intercept: _____

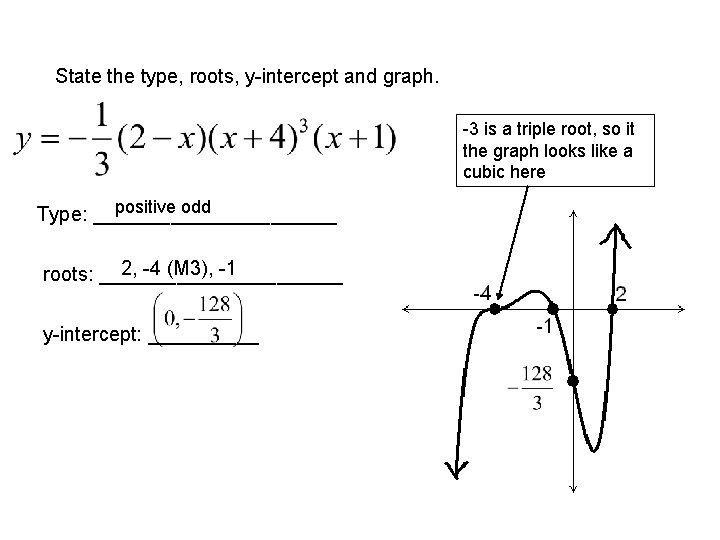
State the type, roots, y-intercept and graph. -3 is a triple root, so it the graph looks like a cubic here positive odd Type: ___________ 2, -4 (M 3), -1 roots: ___________ y-intercept: _____

State the type, roots, y-intercept and graph. Type: ___________ roots: ___________ y-intercept: _____

State the type, roots, y-intercept and graph. Type: ___________ roots: ___________ y-intercept: _____

State the type, roots, y-intercept and graph. Type: ___________ roots: ___________ y-intercept: _____

Graphing Polynomials Day 2

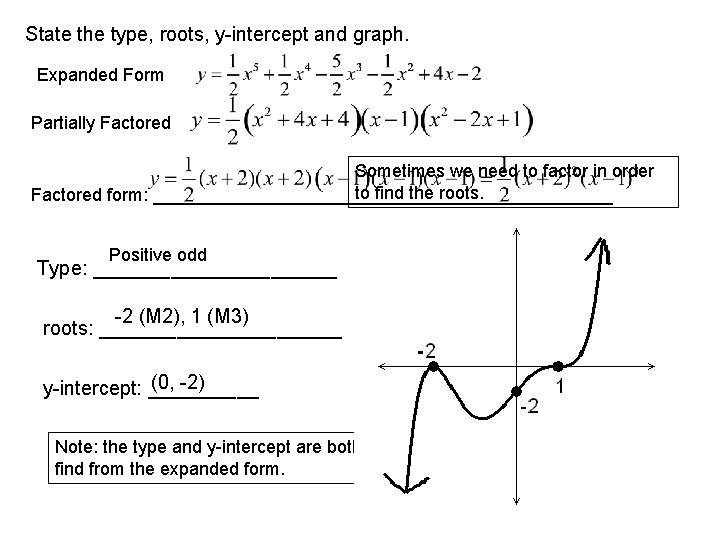
State the type, roots, y-intercept and graph. Expanded Form Partially Factored Sometimes we need to factor in order to find the roots. Factored form: _______________________ Positive odd Type: ___________ -2 (M 2), 1 (M 3) roots: ___________ (0, -2) y-intercept: _____ Note: the type and y-intercept are both easy to find from the expanded form.

State the type, roots, y-intercept and graph. Remember to factor first Type: ___________ roots: ___________ y-intercept: _____

State the type, roots, y-intercept and graph. Type: ___________ roots: ___________ y-intercept: _____

Remember real roots are x-intercepts, but imaginary roots are not. Imaginary roots always come in pairs. Sketch a graph for each description. AAnegative positive negativeeven odd functionwithno 53 roots. real roots