Graphing Polynomials By Deanna Carbone Jacqueline Di Salvatore

Graphing Polynomials By: Deanna Carbone, Jacqueline Di. Salvatore, and Alyssa Fanelli

Definitions • Real Zeros – the value of x when y=0; the y-intercepts • Rational Roots Theorem – p/q is a rational zero of f, a polynomial of degree 1 or higher or the coefficient is an integer • Multiplicity – when there are multiple of the same real zeros [ex: (x+2)2] • Sign Analysis – testing the intervals for values between the real zeros • Maximum – highest y-value and turning point of the graph • Minimum – lowest y-value and turning point of the graph • Y-intercept – point on the graph when y=0 • Intervals of increasing and decreasing – where y increases or decreases on the graph; determined by the change in y, but written using x-values • Degree of a polynomial – highest exponent in the equation

Step 1 Find the real zeros o Factor the equation completely (use Rational Roots Theorem if needed) o Look for multiplicities a. Even multiplicity – graph touches the x-axis b. Odd multiplicity – graph goes through the x-axis

Step 2 Test intervals o Choose values between the real zeros found from Step 1 o Plug these values into each factor of the original polynomial and determine whether the answer is positive or negative o Once all values are tested, multiply the signs of each answer to determine the end behavior o The end behavior should relate to the degree of the polynomial a. Even degree – same end behavior b. Odd degree – opposite end behavior

Step 3 Determine the number of turning points o Subtract 1 from the degree of the polynomial to determine the number of maximums and minimums

Step 4 Graph the polynomial o Find the y-intercept by plugging 0 into the original equation o Graph o Analyze the graph a. X-intercepts b. Maximums and minimums (from calculator) c. Intervals of increasing and decreasing
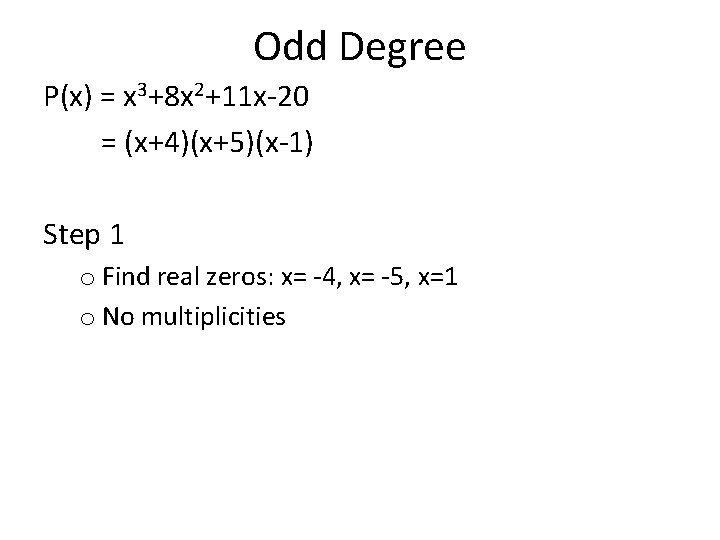
Odd Degree P(x) = x 3+8 x 2+11 x-20 = (x+4)(x+5)(x-1) Step 1 o Find real zeros: x= -4, x= -5, x=1 o No multiplicities

Odd Degree (cont’d) Step 2 o Test intervals -6 -4. 5 x+4 x+5 x-1 - + + 0 2 + + - + +

Odd Degree (cont’d) Step 3 o Find the turning points (Degree – 1) o (3 -1) = 2 turning points Step 4 o Graph (on next slide) o Y-intercept = -20 o X-intercepts = -4, -5, 1 o Max: (-4. 5, 1. 4) o Min: (-. 81, -24. 2) o Intervals of increasing: (-∞, -4. 5] [-. 81, ∞) o Interval of decreasing: [-4. 5, -. 81]
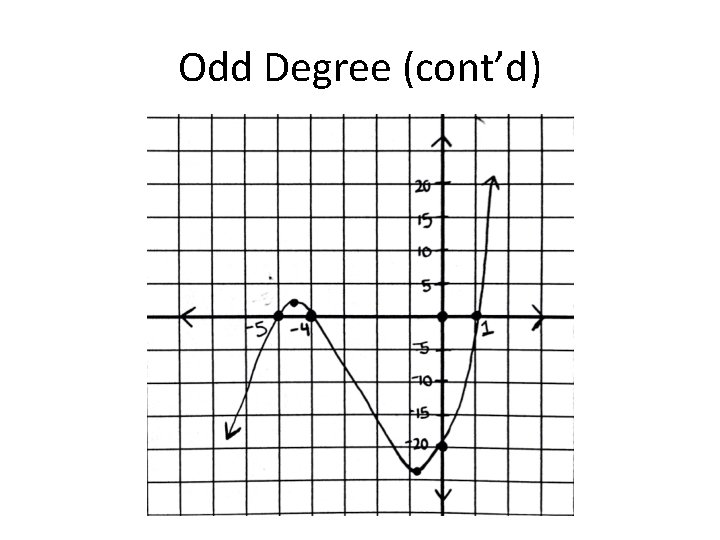
Odd Degree (cont’d)
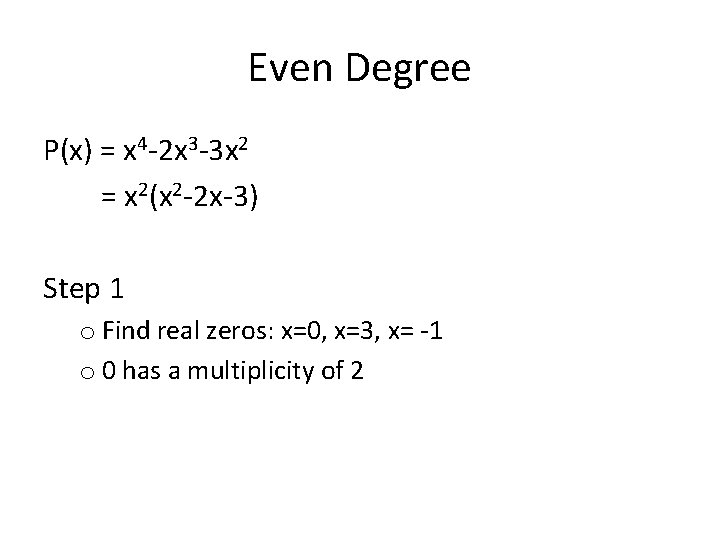
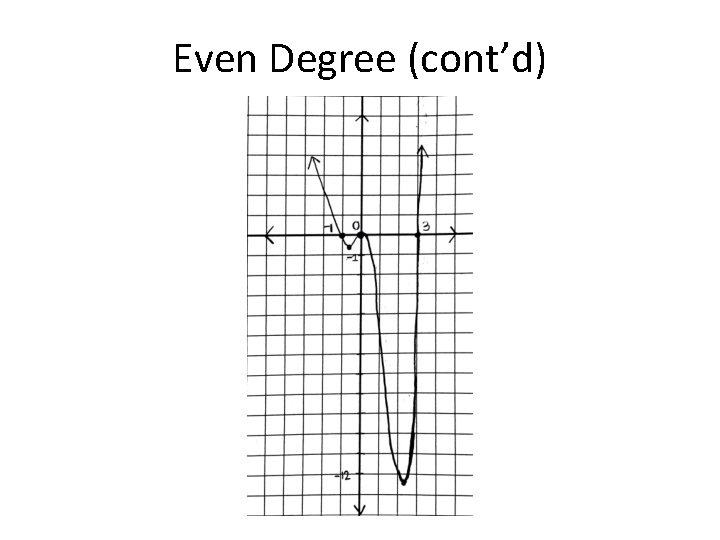
Even Degree P(x) = x 4 -2 x 3 -3 x 2 = x 2(x 2 -2 x-3) Step 1 o Find real zeros: x=0, x=3, x= -1 o 0 has a multiplicity of 2
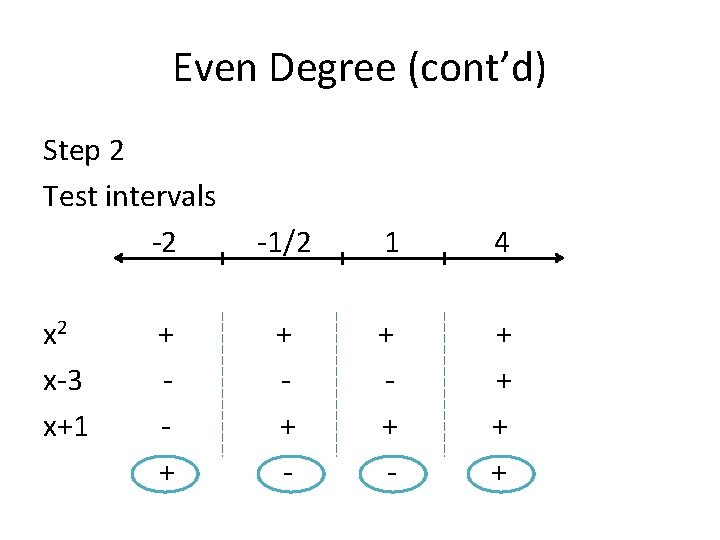
Even Degree (cont’d) Step 2 Test intervals -2 x 2 x-3 x+1 + + -1/2 1 4 + + - + +

Even Degree (cont’d) Step 3 o Find the turning points (Degree-1) o (4 -1) = 3 turning points Step 4 Graph (on next slide) Y-intercept = 0 X-intercepts = 0, 3, -1 Max: (0, 0) Mins: (-. 68, -. 544) (2. 18, -12. 4) o Intervals of increasing: [-. 686, 0] [2. 18, ∞) o Intervals of decreasing: (-∞, -. 686] [0, 2. 18] o o o
Even Degree (cont’d)

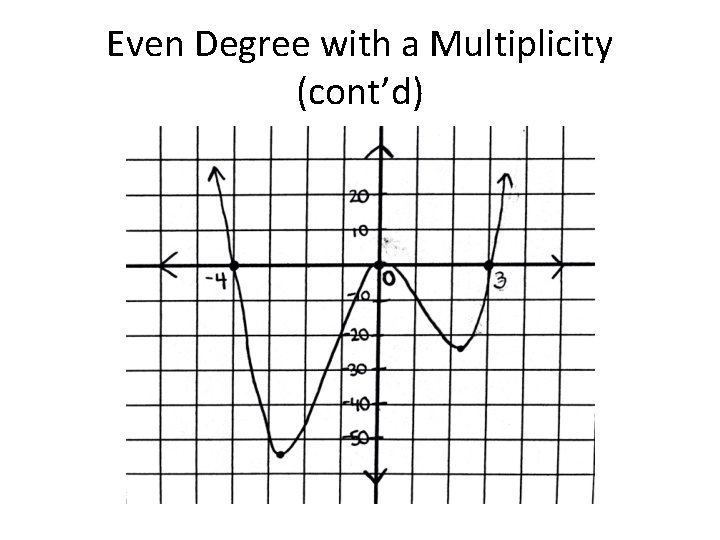
Even Degree with a Multiplicity P(x) = x 4+x 3 -12 x 2 = x 2(x+4)(x-3) Step 1 o Find real zeros: x=0, x= -4, x=3 o 0 has a multiplicity of 2

Even Degree with a Multiplicity (cont’d) Step 2 o Test intervals -5 -1 x 2 x+4 x-3 + + - 1 5 + + - + +

Even Degree with a Multiplicity (cont’d) Step 3 o Find the turning points (Degree-1) o (4 -1) = 3 turning points Step 4 o Graph (on next slide) o Y-intercept = 0 o X-intercepts = -4, 3, 0 o Max: (0, 0) o Mins: (2. 10, -24. 21) (-2. 85, -54. 64) o. Intervals of increasing: [-2. 85, 0], [2. 10, ∞) o. Intervals of decreasing: (-∞, -2. 85], [0, 2. 10]
Even Degree with a Multiplicity (cont’d)
- Slides: 18