Graphing Polynomial Functions Lesson 3 4 Day 2

Learning Targets • Determine key features of a polynomial graph • Use the Leading

Polynomials • What do you remember about polynomials? • What would be key features

Polynomials Graphs of polynomial functions are continuous. That is, they have no breaks, holes

Given the polynomials below, answer the following. . A. What is the degree? B.

Then determine the number of turning points of the graph of the function.

Descartes Rule of Signs says that when the real zeros of a polynomial function

End Behavior: odd degree positive leading coefficient = left falls, right rises Max turning

Perform Rational Root Test again, using the bottom row (quotient) as top row for

Slides: 23

Download presentation

Graphing Polynomial Functions Lesson 3. 4 Day 2 Notes

Learning Targets • Determine key features of a polynomial graph • Use the Leading Coefficient/Degree Test to determine the end behavior of graphs of polynomial functions. • Find and use zeros of polynomial functions as sketching aids

Polynomials • What do you remember about polynomials? • What would be key features of polynomial graphs?

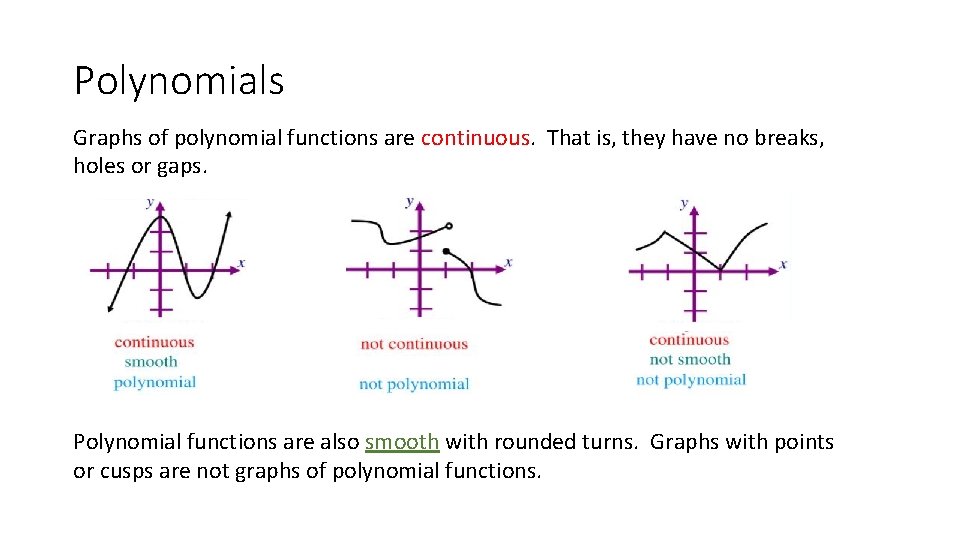
Polynomials Graphs of polynomial functions are continuous. That is, they have no breaks, holes or gaps. Polynomial functions are also smooth with rounded turns. Graphs with points or cusps are not graphs of polynomial functions.

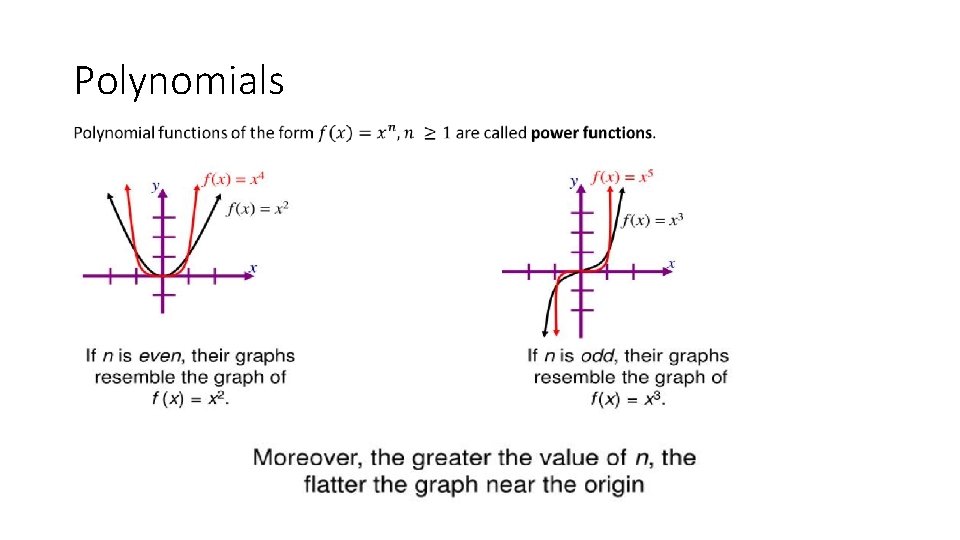
Polynomials

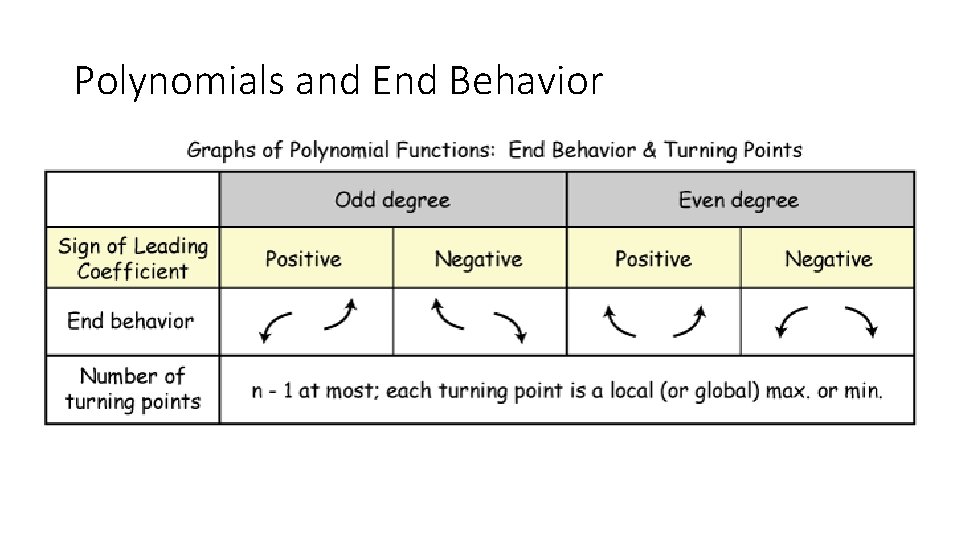
Polynomials and End Behavior

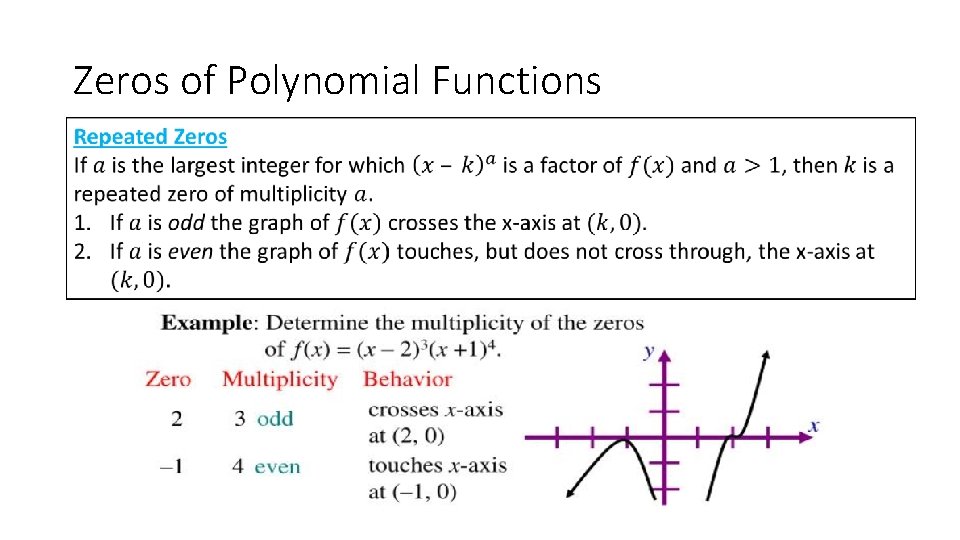
Zeros of Polynomial Functions

Given the polynomials below, answer the following. . A. What is the degree? B. What is its leading coefficient? C. How many “turns” (relative maximums or minimums) could it have (maximum)? D. How many real zeros could it have (maximum)? E. How would you describe the left and right end behavior of the graph of the equation? F. What is its y-intercept?

Zeros of Polynomial Functions

Then determine the number of turning points of the graph of the function.

Zeros of Polynomial Functions

Turning point

Descartes Rule of Signs says that when the real zeros of a polynomial function are put in order, they divide the real number line into intervals in which the function has no sign changes. These resulting intervals are test intervals in which a representative xvalue in the interval is chosen to determine if the value of the polynomial function is positive (the graph lies above the x-axis) or negative (the graph lies below the x-axis).

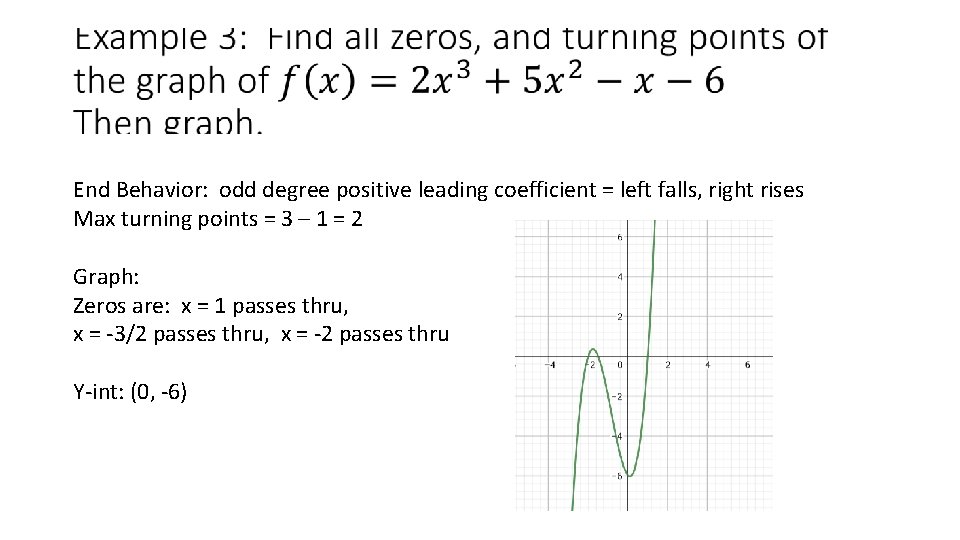
End Behavior: odd degree positive leading coefficient = left falls, right rises Max turning points = 3 – 1 = 2 Graph: Zeros are: x = 1 passes thru, x = -3/2 passes thru, x = -2 passes thru Y-int: (0, -6)

Perform Rational Root Test again, using the bottom row (quotient) as top row for next Synthetic Division

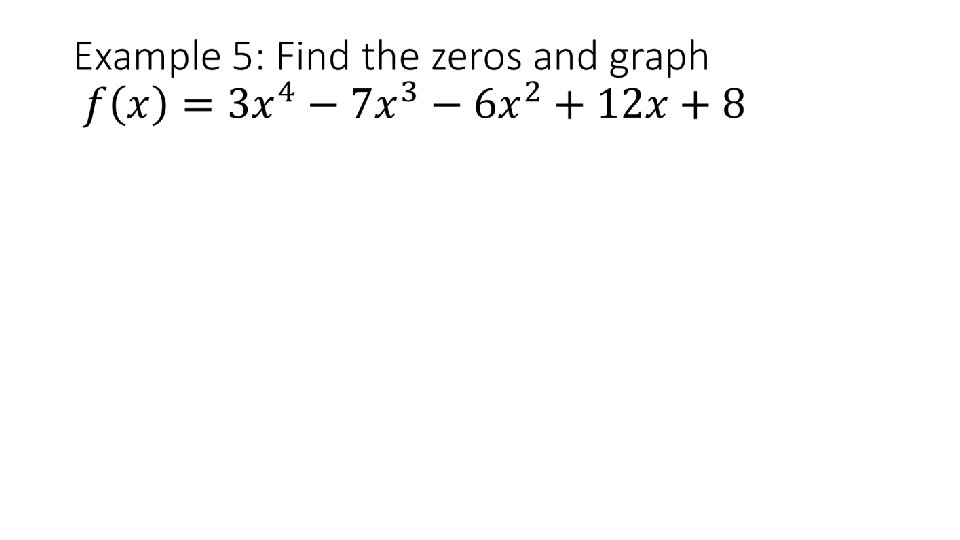
Homework 3. 4 #7, 8, and 36 -46 evens