GRAPHING POINTS FINDING SLOPE Ms Stack Please put

GRAPHING POINTS & FINDING SLOPE Ms. Stack

Please put your signed tests on my desks, thanks! FRIDAY’S DO NOW 1. Solve: 8 x – 10 = 4 x + 26 2. -4 + 3(10 – 5)2 3. How many seconds are in 3 days? 4. How would you re-write x * x * x? 5. What quadrant does the point (-4, 5) lie in?

WHAT IS SLOPE? The slope of a straight line shows how steep the line is. The slope remains constant, meaning it never changes. The slope at one end of a line is the same as at the other end of the line. Slope can be calculated by: m= rise or run Instead of using the word slope, another way to say slope is simply by using the letter m (from y=mx + b) or saying the “rate of change. ”

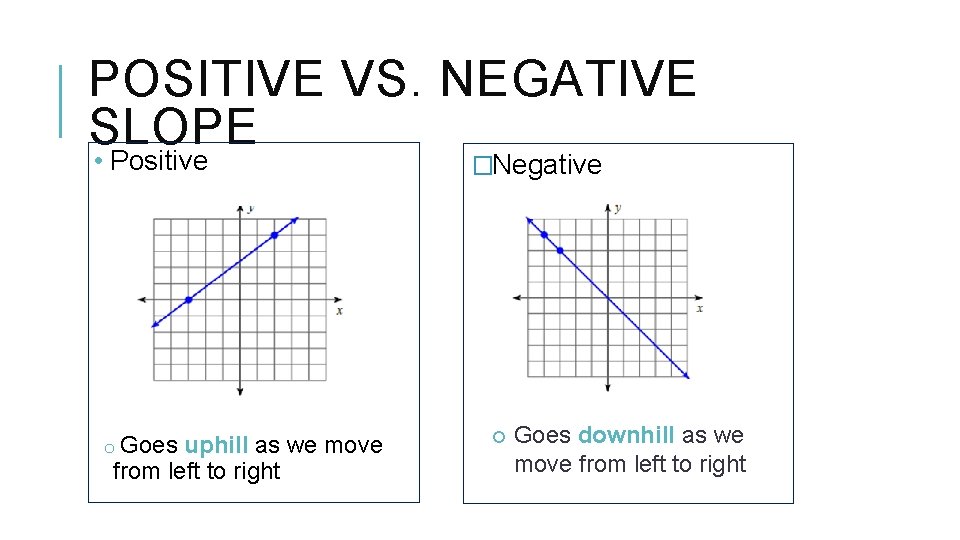
POSITIVE VS. NEGATIVE SLOPE • Positive o Goes uphill as we move from left to right �Negative Goes downhill as we move from left to right

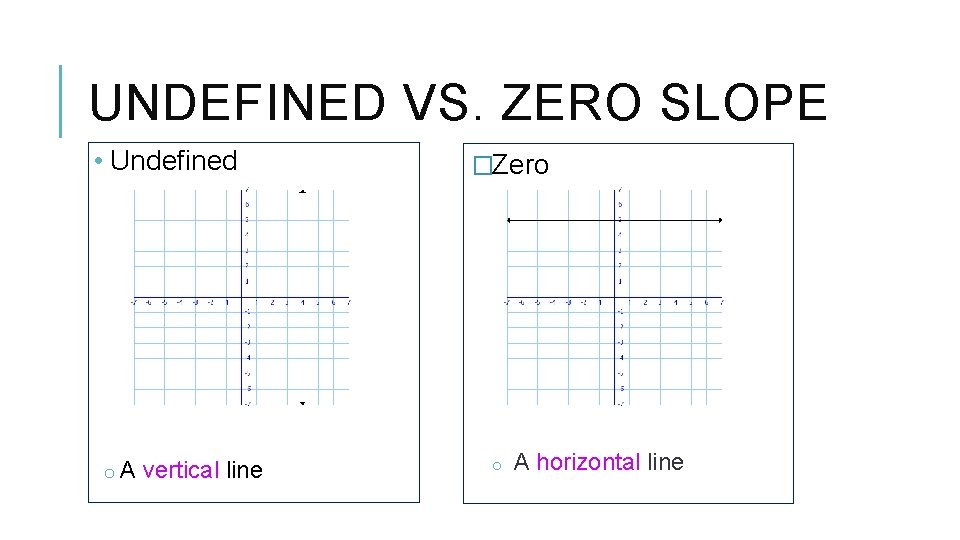
UNDEFINED VS. ZERO SLOPE • Undefined o A vertical line �Zero o A horizontal line

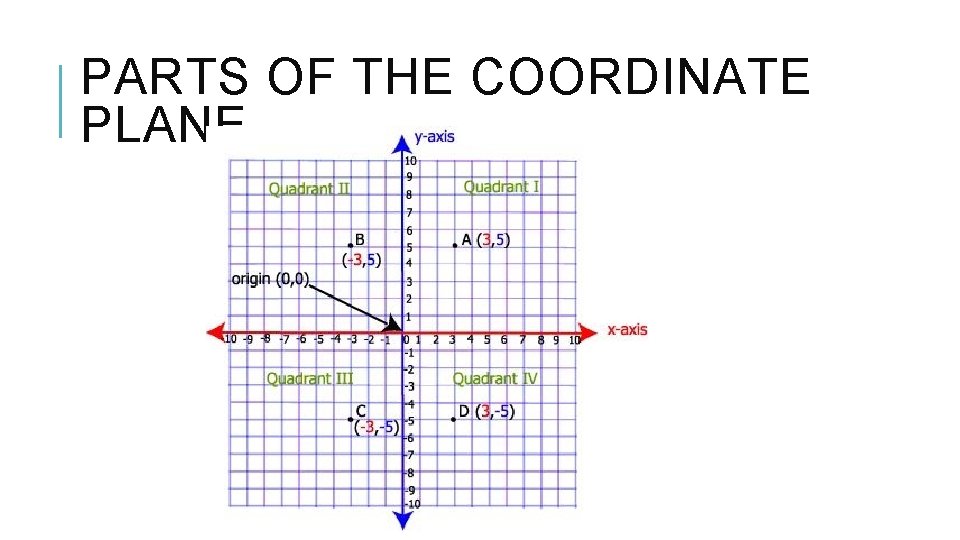
PARTS OF THE COORDINATE PLANE

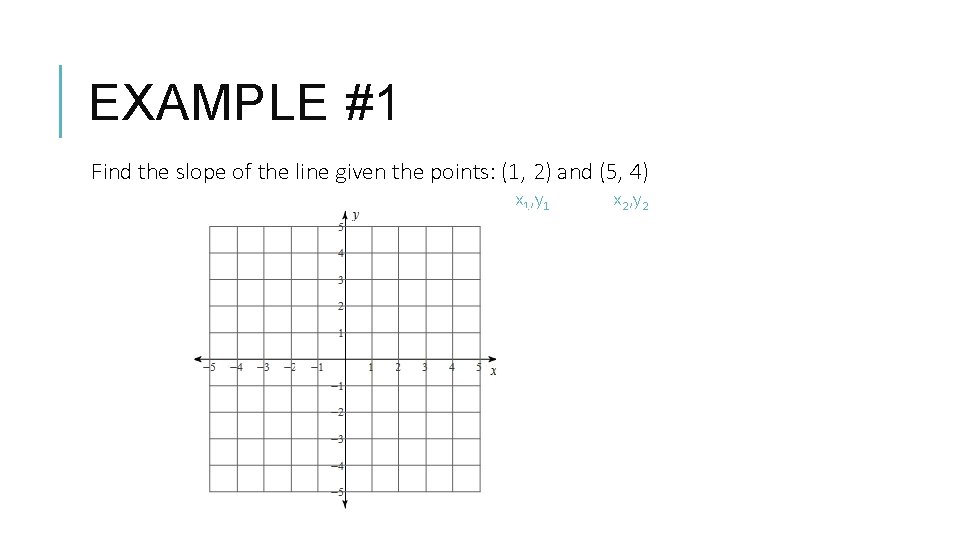
EXAMPLE #1 Find the slope of the line given the points: (1, 2) and (5, 4) x 1, y 1 x 2, y 2

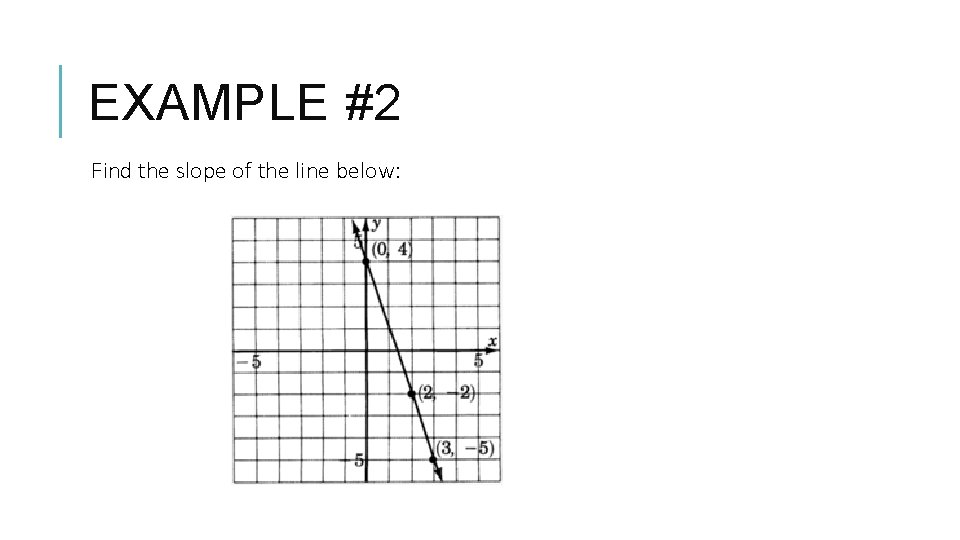
EXAMPLE #2 Find the slope of the line below:

EXAMPLE #3 Find the slope of the line given this table:

EXAMPLE #4 Find the slope of the given line: y= -6 x + 12

EXAMPLE #5 A climber is on a hike. After 2 hours he is at an altitude of 400 feet. After 6 hours, he is at an altitude of 700 feet. What is the average rate of change? *Hint: Write ordered pairs (time, units)

EXAMPLE #6 In 1998, Jimmy weighed 300 lbs. In 2010, the he weighed 180 lbs. What was the rate of change in weight? *Hint: Write ordered pairs (time, weight)

LET’S PRACTICE • Directions: Plot the set of ordered pairs on graph paper, connect the points to form a line and then find the slope of the line 1. (2, 3) (4, 5) 2. (3, 2) (3, 6) 3. (1, -3) (-2, 4) 4. (6, -2) (3, -2)

EXTRA CREDIT § Your extra credit is due on Monday 9/21 § You must show all of your work to receive credit § If you have questions, you have time to ask me before Monday *Call me/ text me/ email me § The extra credit is worth 20 points & the maximum score you can earn on your test from the EC is an 80%

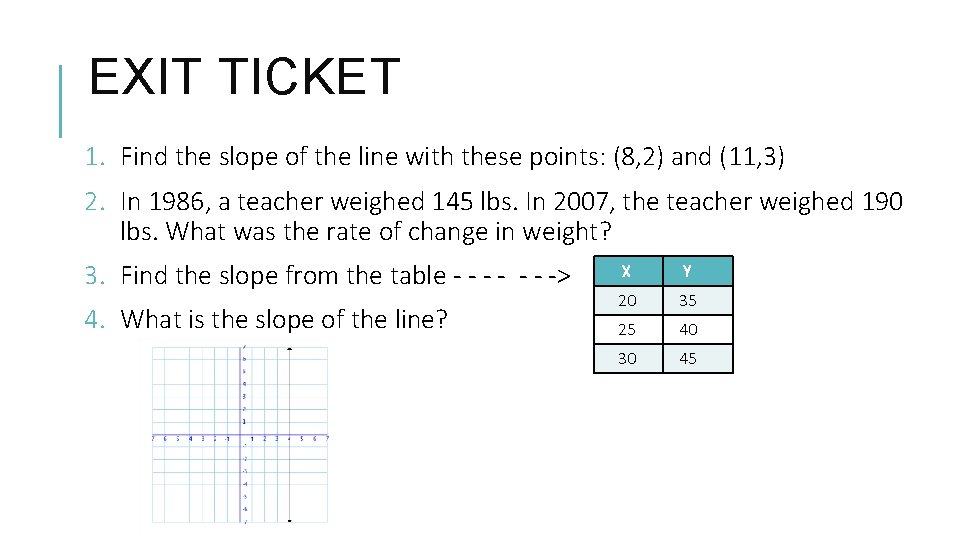
EXIT TICKET 1. Find the slope of the line with these points: (8, 2) and (11, 3) 2. In 1986, a teacher weighed 145 lbs. In 2007, the teacher weighed 190 lbs. What was the rate of change in weight? 3. Find the slope from the table - - - -> 4. What is the slope of the line? X Y 20 35 25 40 30 45