Graphing Parabolas Using the Vertex Axis of Symmetry

Graphing Parabolas Using the Vertex Axis of Symmetry & y-Intercept By: Jeffrey Bivin Lake Zurich High School jeff. bivin@lz 95. org Last Updated: October 15, 2007

Graphing Parabolas • With your graphing calculator, graph each of the following quadratic equations and identify the vertex and axis of symmetry. y = x 2 + 4 x - 7 y = 2 x 2 + 10 x + 4 y = -3 x 2 + 5 x + 9 Jeff Bivin -- LZHS

Graph the following parabola y = x 2 + 4 x - 7 vertex: axis of symmetry: y-intercept: Jeff Bivin -- LZHS

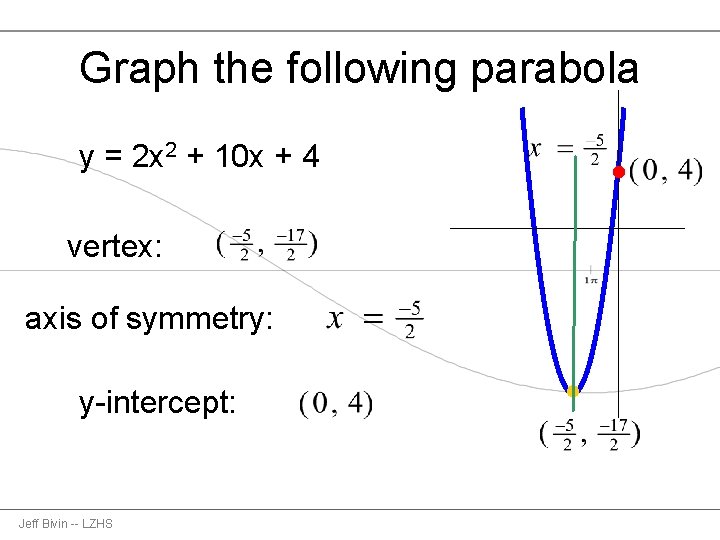
Graph the following parabola y = 2 x 2 + 10 x + 4 vertex: axis of symmetry: y-intercept: Jeff Bivin -- LZHS

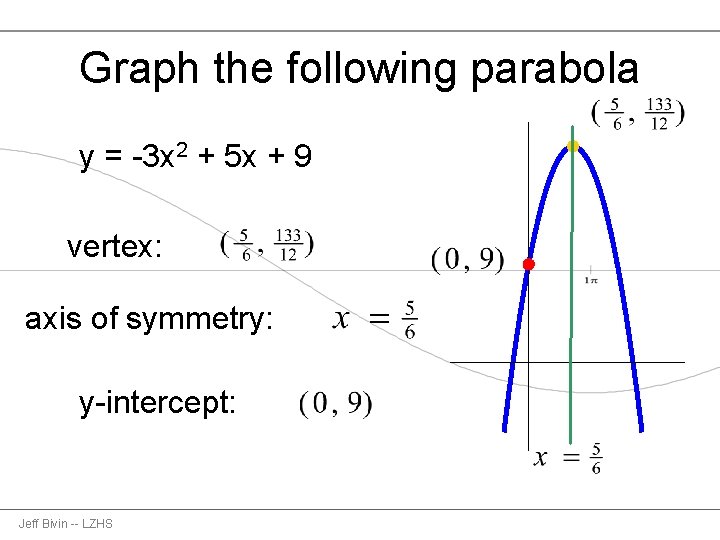
Graph the following parabola y = -3 x 2 + 5 x + 9 vertex: axis of symmetry: y-intercept: Jeff Bivin -- LZHS

Graphing Parabolas • Now look at the coefficients of the equation and the value of the axis of symmetry – especially a and b • y = ax 2 + bx + c y = x 2 + 4 x - 7 y = 2 x 2 + 10 x + 4 y = -3 x 2 + 5 x + 9 Jeff Bivin -- LZHS

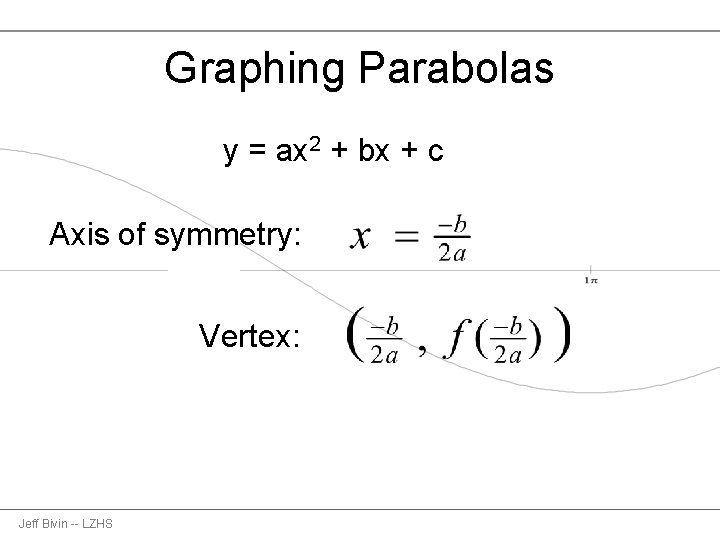
Graphing Parabolas y = ax 2 + bx + c Axis of symmetry: Vertex: Jeff Bivin -- LZHS

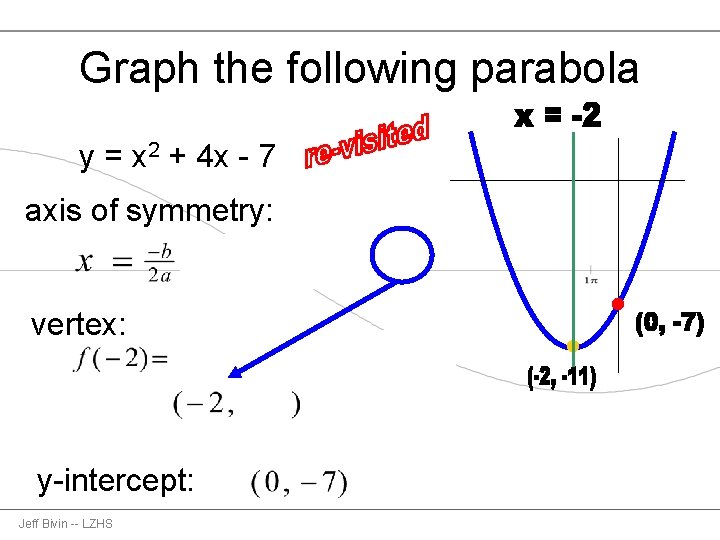
Graph the following parabola y = x 2 + 4 x - 7 axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

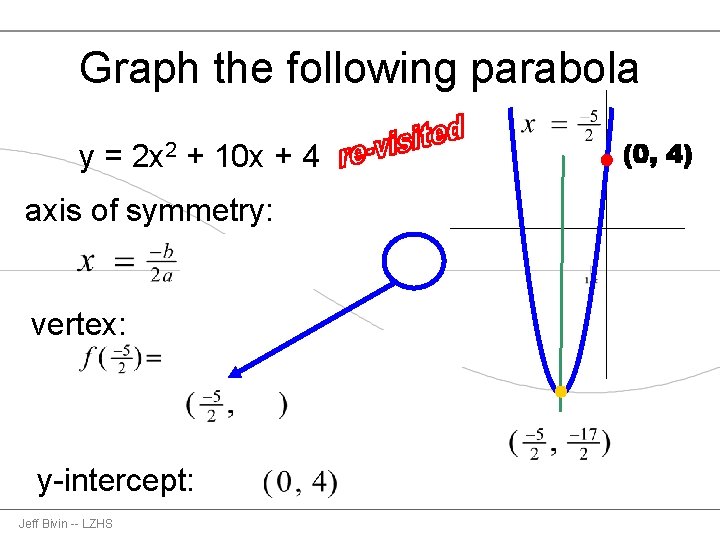
Graph the following parabola y = 2 x 2 + 10 x + 4 axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

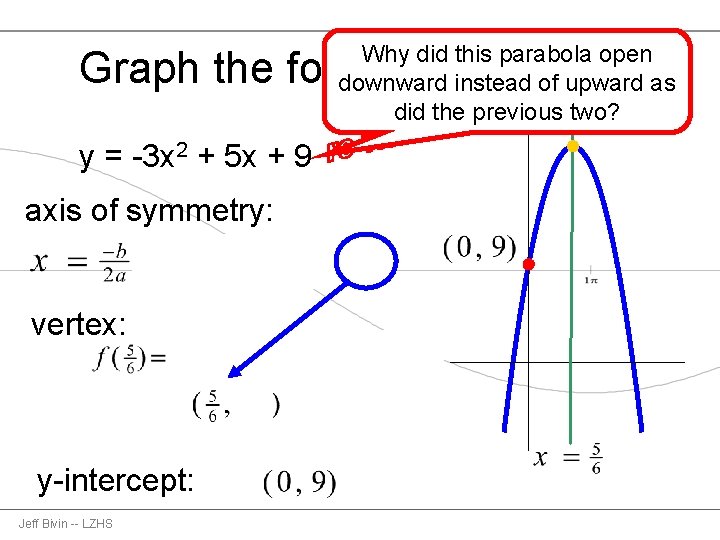
Why did this parabola open downward instead of upward as did the previous two? Graph the following parabola y = -3 x 2 + 5 x + 9 axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

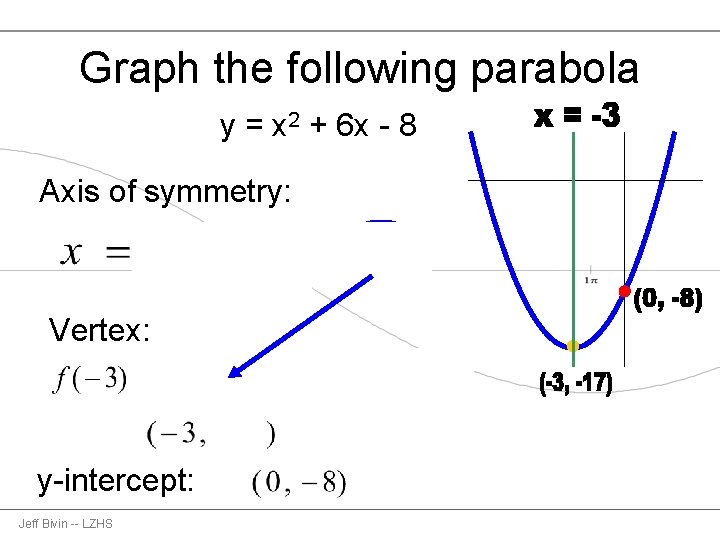
Graph the following parabola y = x 2 + 6 x - 8 Axis of symmetry: Vertex: y-intercept: Jeff Bivin -- LZHS

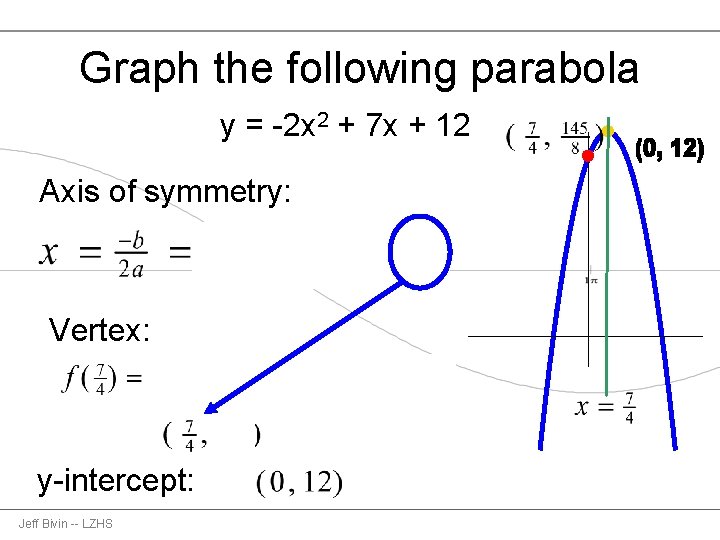
Graph the following parabola y = -2 x 2 + 7 x + 12 Axis of symmetry: Vertex: y-intercept: Jeff Bivin -- LZHS

Graphing Parabolas In Vertex Form Jeff Bivin -- LZHS

Graphing Parabolas • With your graphing calculator, graph each of the following quadratic equations and identify the vertex and axis of symmetry. vertex axis of sym. y = x 2 y = (x - 5)2 - 4 y = -3(x + 2)2 + 5 y = ⅜(x - 3)2 + 1 Jeff Bivin -- LZHS

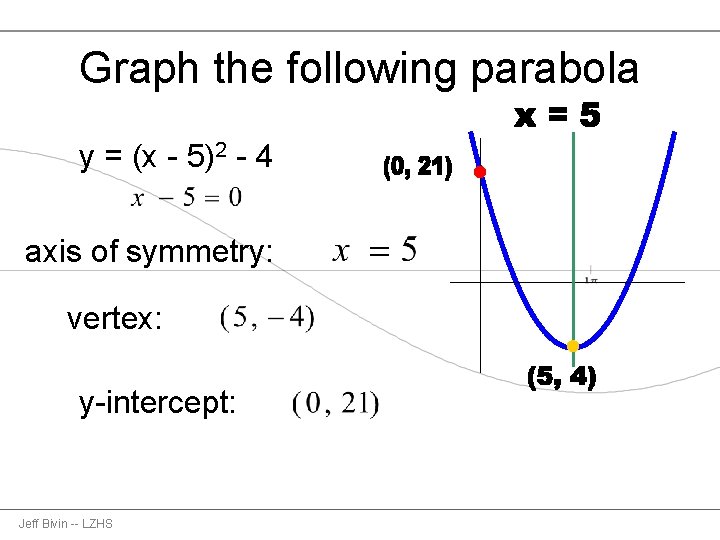
Graph the following parabola y = (x - 5)2 - 4 axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

Graph the following parabola y = -3(x + 2)2 + 5 axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

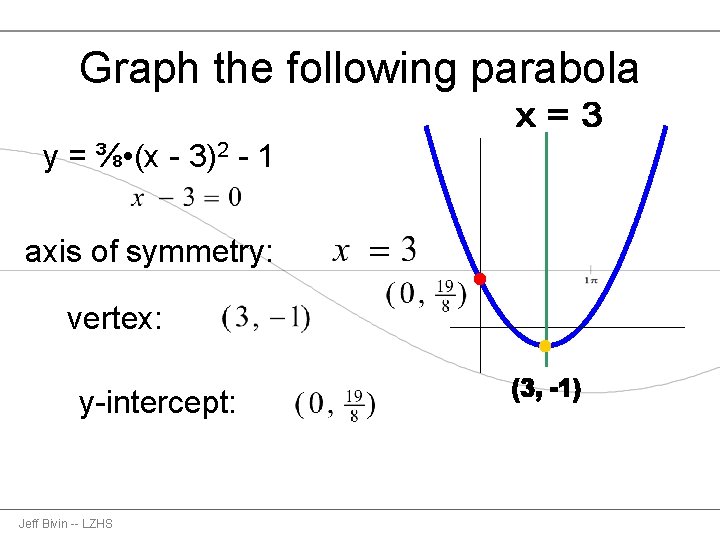
Graph the following parabola y = ⅜ • (x - 3)2 - 1 axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

Graphing Parabolas In Intercept Form Jeff Bivin -- LZHS

Graph the following parabola y = (x – 4)(x + 2) x-intercepts: axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

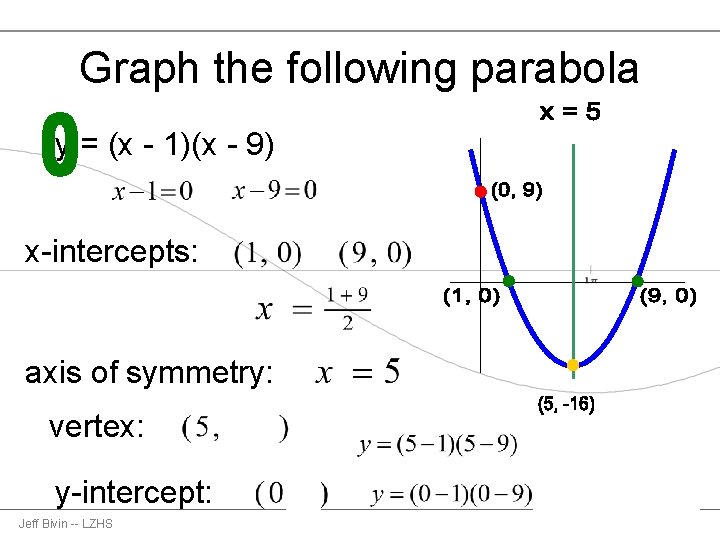
Graph the following parabola y = (x - 1)(x - 9) x-intercepts: axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

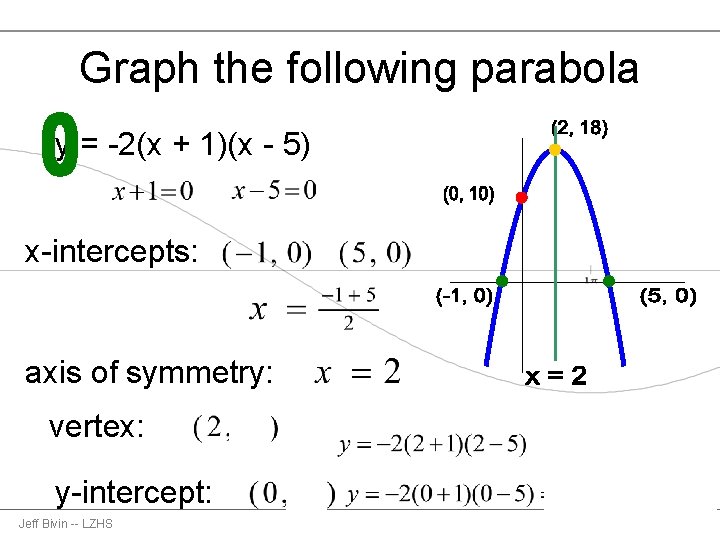
Graph the following parabola y = -2(x + 1)(x - 5) x-intercepts: axis of symmetry: vertex: y-intercept: Jeff Bivin -- LZHS

Convert to standard form y = -2(x + 1)(x - 5) y = -2(x 2 – 5 x + 1 x – 5) y = -2(x 2 – 4 x – 5) y = -2 x 2 + 8 x + 10 Jeff Bivin -- LZHS

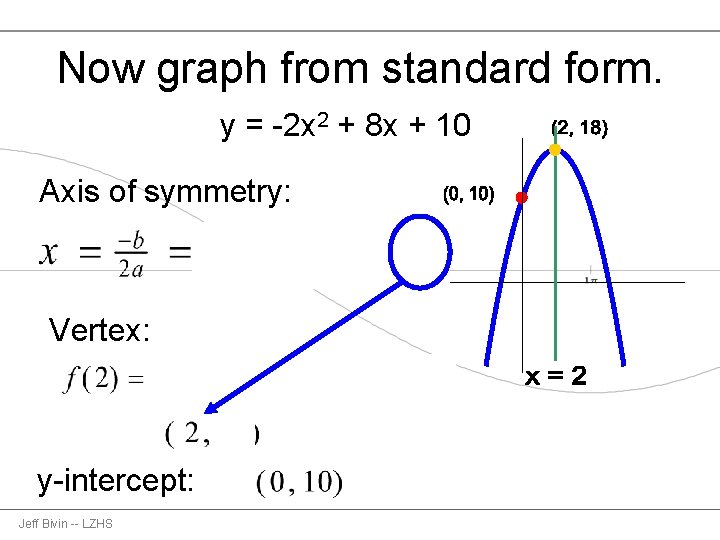
Now graph from standard form. y = -2 x 2 + 8 x + 10 Axis of symmetry: Vertex: y-intercept: Jeff Bivin -- LZHS

A taxi service operates between two airports transporting 200 passengers a day. The charge is $15. 00. The owner estimates that 10 passengers will be lost for each $2 increase in the fare. What charge would be most profitable for the service? What is the maximum income? VERTEX Define the variable x = number of $2 price increases f(x) = income Vertex is: Income = Price ● Quantity f(x) = ( 15 + 2 x ) ( 200 – 10 x ) 15 + 2 x = 0 200 – 10 x = 0 2 x = -15 200 = 10 x So, price = (15 + 2 x) = (15 + 2(6. 25)) = 15 + 12. 5 = $27. 50 Maximum 137. 50 27. 50 income: Jeff Bivin -- LZHS

A taxi service operates between two airports transporting 200 passengers a day. The charge is $15. 00. The owner estimates that 10 passengers will be lost for each $2 increase in the fare. What charge would be most profitable for the service? What is the maximum income? VERTEX Define the variable x = number of $2 price increases f(x) = income Income = Price ● Quantity f(x) = ( 15 + 2 x ) ( 200 – 10 x ) f(x) = 3000 – 150 x + 400 x – 20 x 2 f(x) = – 20 x 2 + 250 x + 3000 f(6. 25) = – 20(6. 25)2 + 250(6. 25) + 3000 Vertex is: f(6. 25) = 3781. 25 So, price = (15 + 2 x) = (15 + 2(6. 25)) = 15 + 12. 5 = $27. 50 Maximum income = f(x) = $3781. 25 Jeff Bivin -- LZHS