GRAPHING LOGARITHMIC FUNCTIONS Natural Logs Objectives Describe how

GRAPHING LOGARITHMIC FUNCTIONS & Natural Logs

Objectives • Describe how exponential functions and logarithmic functions are inverses of each other. • Describe the graphical relationship between a function and its inverse. • Describe how the graphs of logarithmic functions are translated horizontally and vertically. • Use logarithms to solve an equation containing a variable exponent.

� � � The inverse function of an exponential function is the logarithmic function. For all positive real numbers x and b, b>0 and b 1, y=logbx if and only if x=by. The domain of the logarithmic function is • The range of the function is • Since the log function is the inverse of the exponential function, their graphs are symmetric with respect to the line y=x.
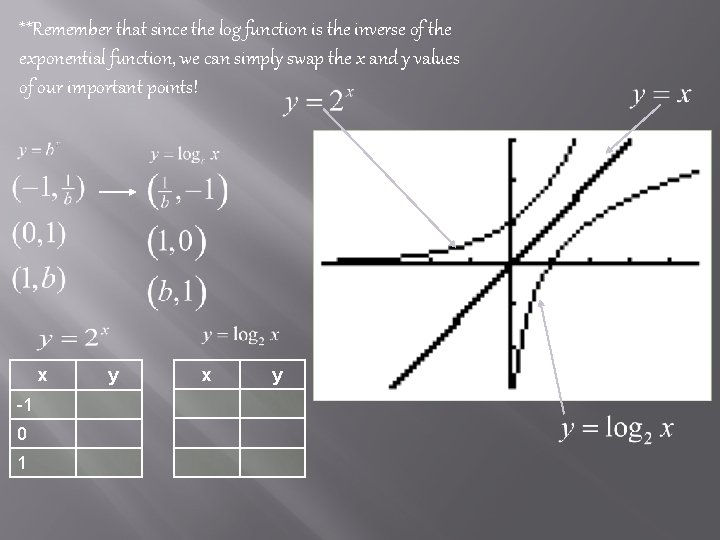
**Remember that since the log function is the inverse of the exponential function, we can simply swap the x and y values of our important points! x -1 0 1 y x y

• Logarithmic Functions where b>1 are ______, • • • one-to-one functions. Logarithmic Functions where 0<b<1 are _____, one-to-one functions. The parent form of the graph has an x-intercept at (1, 0) and passes through _____and _______ There is a vertical asymptote at _______. The value of b determines the flatness of the curve. The function is neither even nor odd. There is ______ symmetry. There is _____ local extrema.
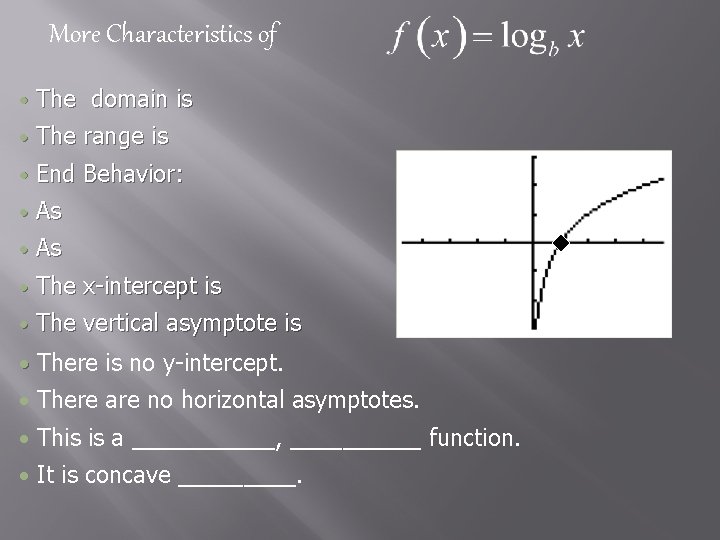
More Characteristics of • The domain is • The range is • End Behavior: • As • The x-intercept is • The vertical asymptote is • There is no y-intercept. • There are no horizontal asymptotes. • This is a ______, _____ function. • It is concave _____.
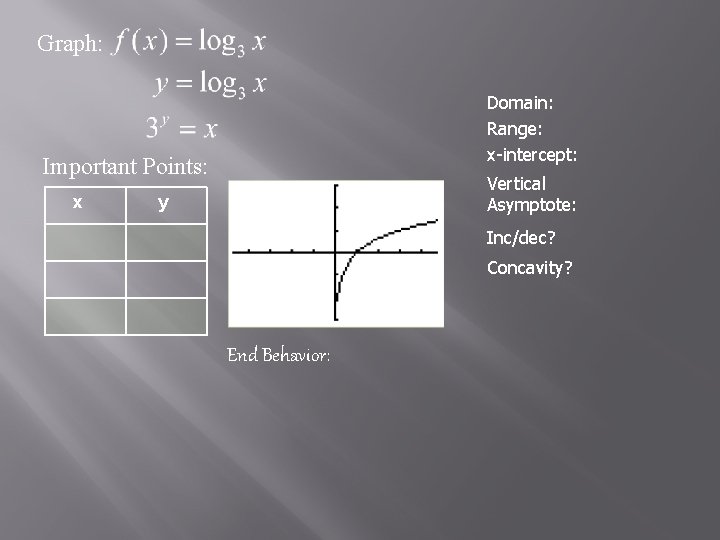
Graph: Domain: Range: x-intercept: Important Points: x Vertical Asymptote: y Inc/dec? Concavity? End Behavior:
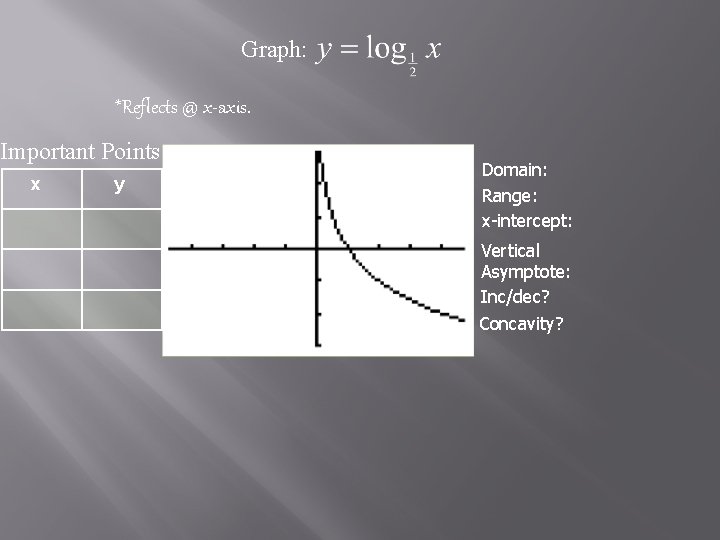
Graph: *Reflects @ x-axis. Important Points: x y Domain: Range: x-intercept: Vertical Asymptote: Inc/dec? Concavity?
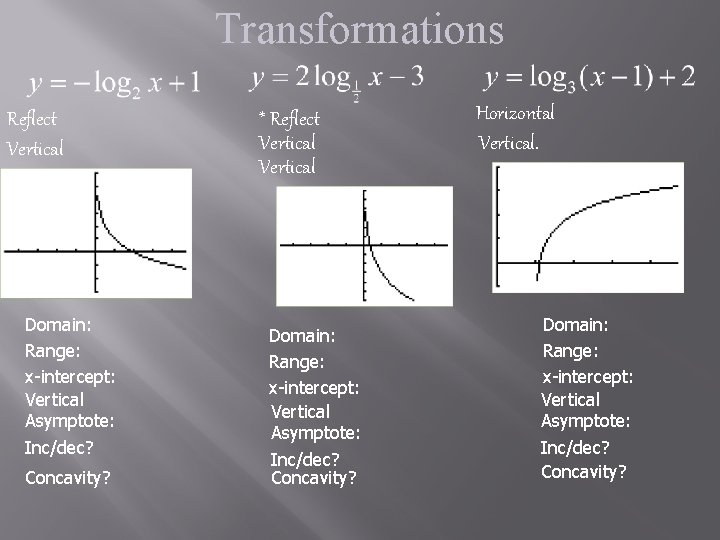
Transformations Reflect Vertical Domain: Range: x-intercept: Vertical Asymptote: Inc/dec? Concavity? * Reflect Vertical Domain: Range: x-intercept: Vertical Asymptote: Inc/dec? Concavity? Horizontal Vertical. Domain: Range: x-intercept: Vertical Asymptote: Inc/dec? Concavity?

The asymptote of a logarithmic function of this form is the line To find an x-intercept in this form, let y=o in the equation To find a y-intercept in this form, let x=o in the equation is the vertical asymptote. Since this is not possible, there is No y-intercept. is the x-intercept
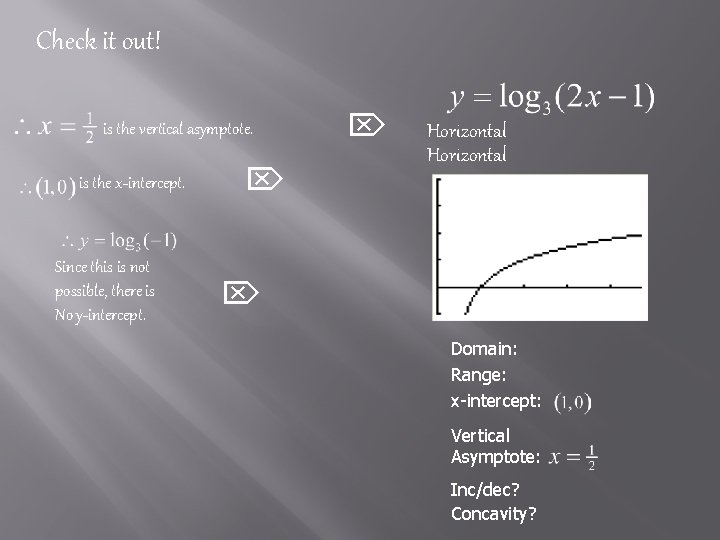
Check it out! is the vertical asymptote. is the x-intercept. Since this is not possible, there is No y-intercept. Horizontal Domain: Range: x-intercept: Vertical Asymptote: Inc/dec? Concavity?
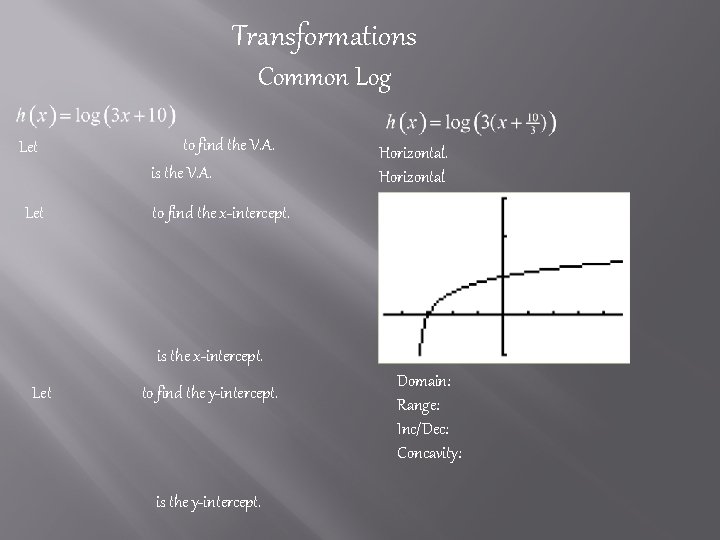
Transformations Common Log Let to find the V. A. is the V. A. Let to find the x-intercept. Horizontal is the x-intercept. Let to find the y-intercept. is the y-intercept. Domain: Range: Inc/Dec: Concavity:
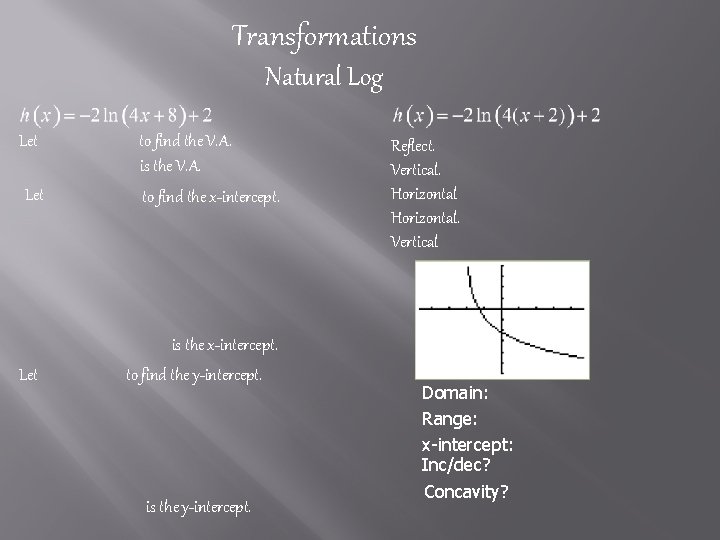
Transformations Natural Log Let to find the V. A. is the V. A. Let to find the x-intercept. Let is the x-intercept. to find the y-intercept. is the y-intercept. Reflect. Vertical. Horizontal. Vertical Domain: Range: x-intercept: Inc/dec? Concavity?

Change of Base Formula Use this formula for entering logs with bases other than 10 or e in your graphing calculator. So, if you wanted to graph , you would enter in your calculator. Either the natural or common log may be used in the change of base formula. So, you could also enter in Your calculator.
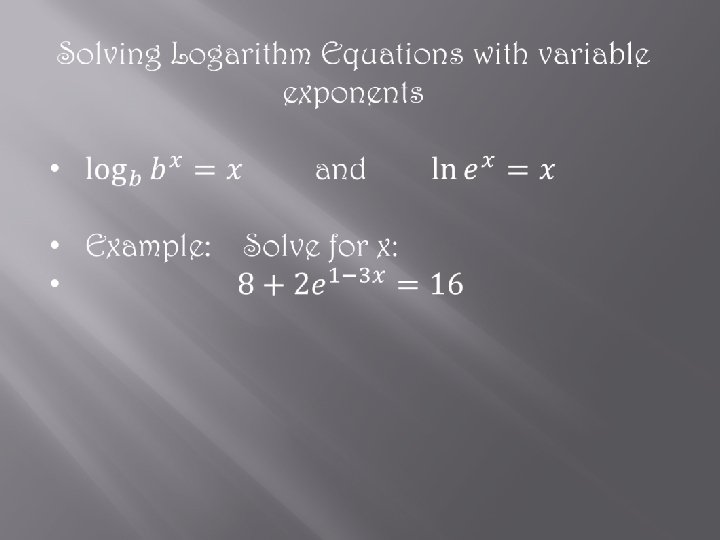
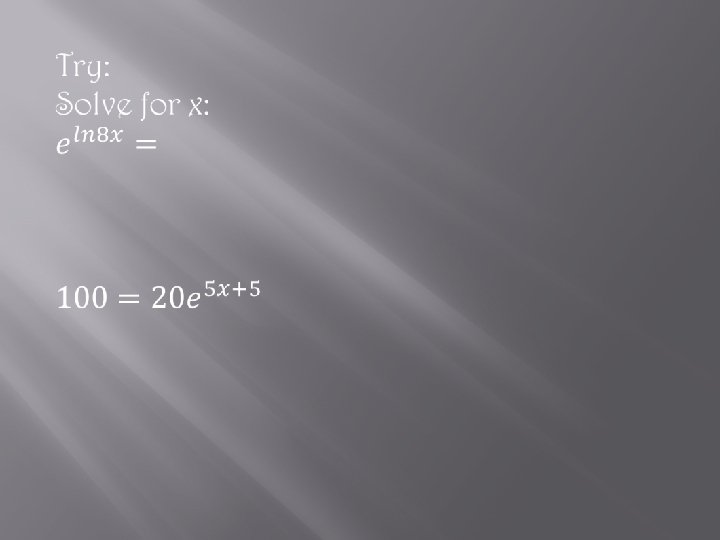


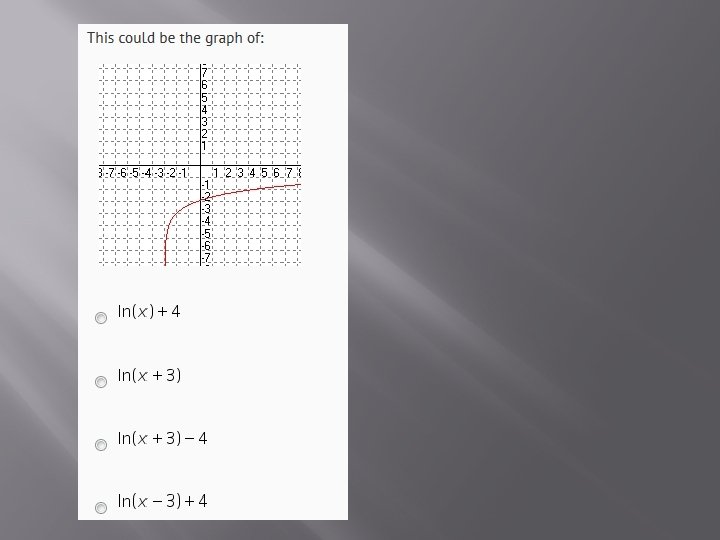




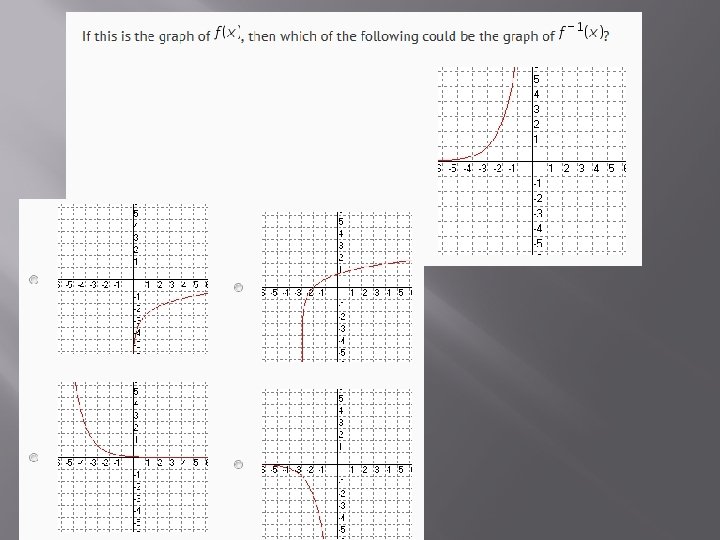


- Slides: 26