Graphing Linear Equations Linear Equation An equation for




























- Slides: 31

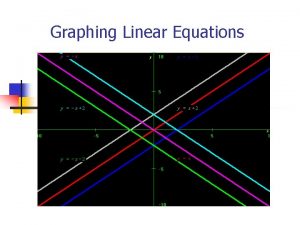
Graphing Linear Equations

Linear Equation An equation for which the graph is a line

Solution Any ordered pair of numbers that makes a linear equation true. (9, 0) IS ONE SOLUTION FOR Y = X - 9

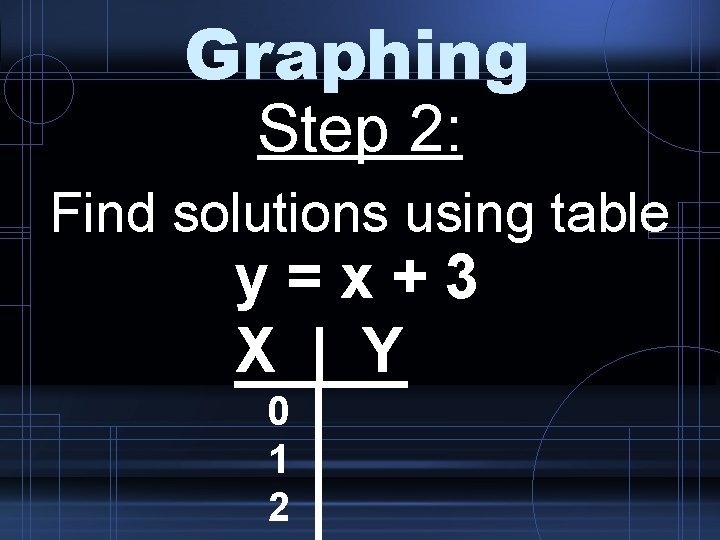
Linear Equation Example: y=x+3

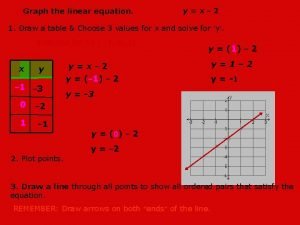
Graphing Step 1: ~ Three Point Method ~ Choose 3 values for x

Graphing Step 2: Find solutions using table y=x+3 X | Y 0 1 2

Graphing Step 3: Graph the points from the table (0, 3) (1, 4) (2, 5)

Graphing Step 4: Draw a line to connect them

Try These • Graph using a table (3 point method) 1) y = x + 3 2) y = x - 4

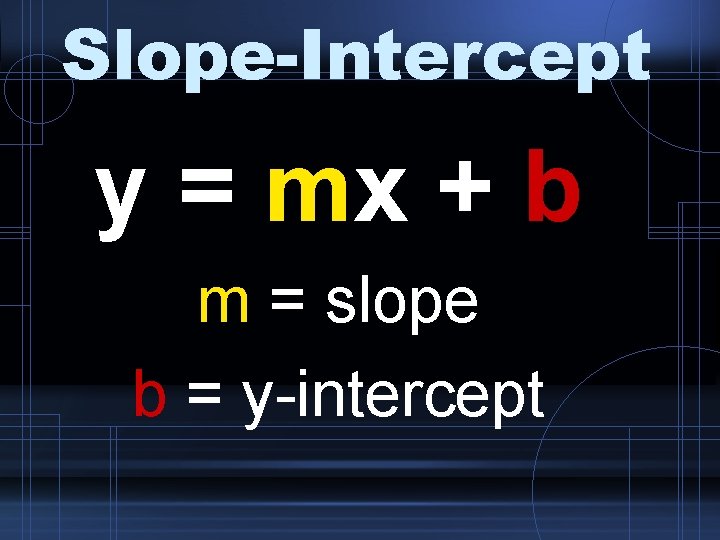
Slope-Intercept y = mx + b m = slope b = y-intercept

Slope-Intercept • The m in the slope-intercept form is ALWAYS attached to the X variable. • The slope is NEVER including the X variable • For example, if given y = 3 x + 4 the slope is 3 NOT 3 x.

Y-intercept Where the line crosses the y -axis

Y-intercept The y-intercept has an x-coordinate of ZERO

Y-intercept To find the yintercept, plug in ZERO for x and solve

Y-Intercept Summary • The y-intercept is the b in the slope intercept form. • This b (y-intercept) is your starting point on the graph. – To easily remember this, think of b as you Beginning point. • For example, in y = 3 x + 4 the Beginning point is at (0, 4) {Remember: to find the yintercept, plug on zero for the x. }

X-intercept Where the line crosses the x -axis

X-intercept The x-intercept has a y coordinate of ZERO

X-intercept To find the xintercept, plug in ZERO for y and solve

Slope Describes the steepness of a line

Slope Equal to: Rise Run

Rise The change vertically, the change in y

Run The change horizontally or the change in x

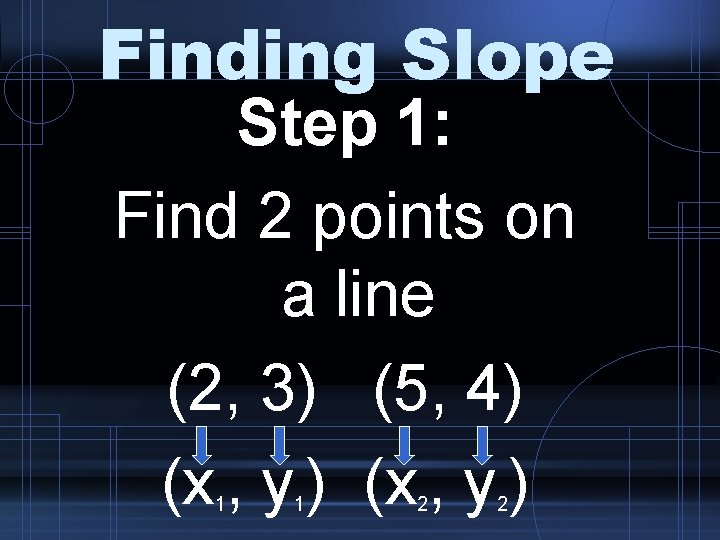
Finding Slope Step 1: Find 2 points on a line (2, 3) (5, 4) (x , y ) 1 1 2 2

Finding Slope Step 2: Find the RISE between these 2 points Y-Y = 2 1 4 -3=1

Finding Slope Step 3: Find the RUN between these 2 points X-X = 2 1 5 -2=3

Finding Slope Step 4: Write the RISE over RUN as a ratio Y-Y 2 1 X-X 2 1 = 1 3

Step 1: Mark a point on the y-intercept

Step 2: Define slope as a fraction. . .

Step 3: Numerator is the vertical change (RISE)

Step 4: Denominator is the horizontal change (RUN)

Step 5: Graph at least 3 points and connect the dots
 4-5 graphing linear equations
4-5 graphing linear equations Graphing linear equations definition
Graphing linear equations definition Lesson 5 graphing linear equations and inequalities
Lesson 5 graphing linear equations and inequalities Standard form of a linear equation definition
Standard form of a linear equation definition Graphing linear equations vocabulary
Graphing linear equations vocabulary 1/x graph
1/x graph Persamaan diferensial simultan
Persamaan diferensial simultan Difference between linear and nonlinear analysis
Difference between linear and nonlinear analysis Persamaan linier 1 variabel
Persamaan linier 1 variabel Graphing systems of nonlinear equations
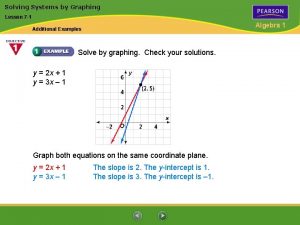
Graphing systems of nonlinear equations Lesson 7 solve systems of equations by graphing
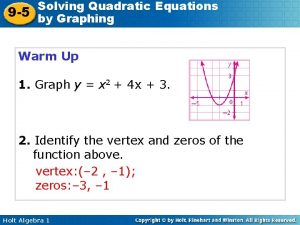
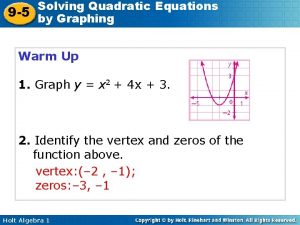
Lesson 7 solve systems of equations by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing Objectives of quadratic equation
Objectives of quadratic equation Lesson 7 - graphing radical equations and inequalities
Lesson 7 - graphing radical equations and inequalities 9-3 practice solving quadratic equations by graphing
9-3 practice solving quadratic equations by graphing 9-2 solving quadratic equations by graphing
9-2 solving quadratic equations by graphing How to find roots of equation
How to find roots of equation Y=ax2+bx+c equation
Y=ax2+bx+c equation Linear equations
Linear equations 6-1 graphing systems of equations answers
6-1 graphing systems of equations answers 4-1 graphing equations in slope intercept form
4-1 graphing equations in slope intercept form 8-1 identifying quadratic functions
8-1 identifying quadratic functions How to write an equation in slope intercept form
How to write an equation in slope intercept form 2-7 solving equations by graphing
2-7 solving equations by graphing Lesson 2-1 graphing two-variable equations
Lesson 2-1 graphing two-variable equations Graphing absolute value equations
Graphing absolute value equations 5-2 solving quadratic equations by graphing
5-2 solving quadratic equations by graphing 1-5 solving equations and inequalities by graphing
1-5 solving equations and inequalities by graphing Lesson 1-5 solving equations and inequalities by graphing
Lesson 1-5 solving equations and inequalities by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing How to rewrite absolute value as piecewise function
How to rewrite absolute value as piecewise function