Graphing Linear Equations In Standard Form Ax By
Graphing Linear Equations In Standard Form Ax + By = C

Linear equations have two variables and when we plot all the (x, y) pairs that make the equation true we get a line. We will use The Standard Form of the equation to graph the line.

The formula for Standard Form is: We can find 3 things just by looking at the formula: Ax + By = C To find where the line crosses each axis, let the other value be zero. • If y is zero, we have Ax = C is the x-intercept. • If x is zero, we have By = C is the y-intercept. A • −— is the slope. B Using the x-intercept and/or y-intercept as a starting point, you can use the slope to graph more points on the line of the equation.

These equations are all in Standard Form: 2 x – y = -1 x + y = -4 3 x – 2 y = 4 Notice that these equations are all in the form Ax + By = C.
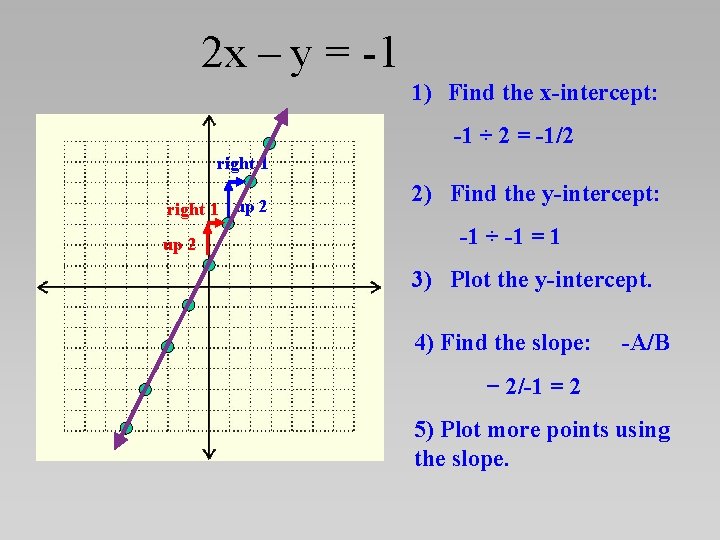
2 x – y = -1 1) Find the x-intercept: -1 ÷ 2 = -1/2 right 1 up 2 2) Find the y-intercept: -1 ÷ -1 = 1 3) Plot the y-intercept. 4) Find the slope: -A/B − 2/-1 = 2 5) Plot more points using the slope.
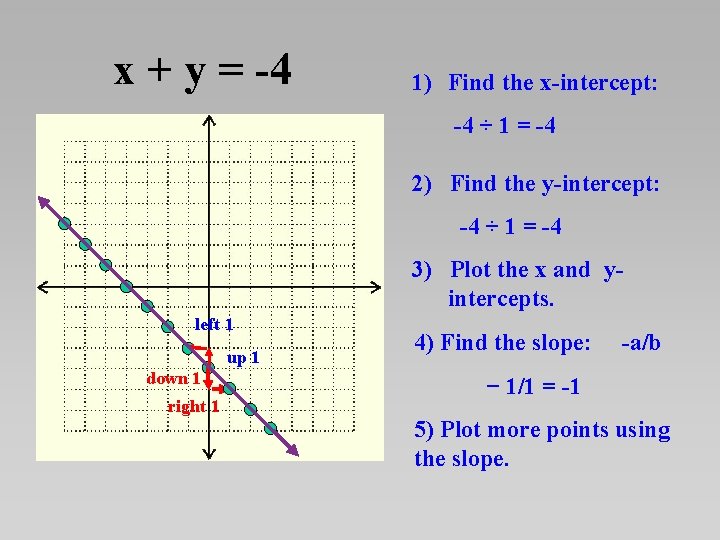
x + y = -4 1) Find the x-intercept: -4 ÷ 1 = -4 2) Find the y-intercept: -4 ÷ 1 = -4 3) Plot the x and yintercepts. left 1 up 1 down 1 right 1 4) Find the slope: -a/b − 1/1 = -1 5) Plot more points using the slope.
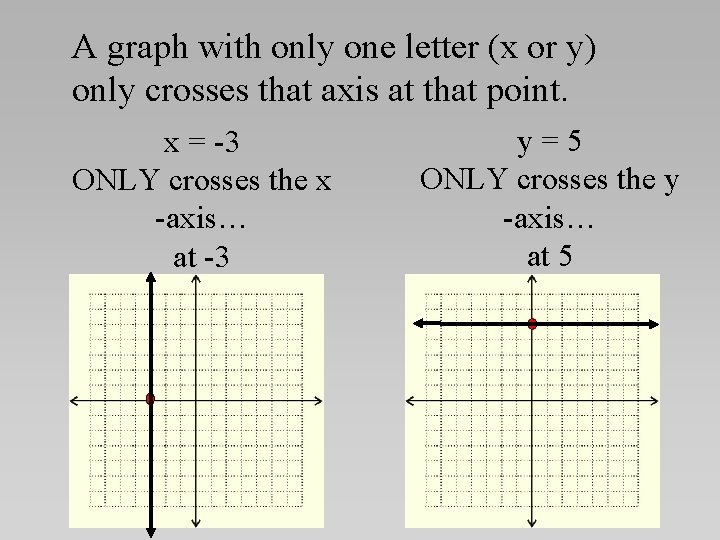
A graph with only one letter (x or y) only crosses that axis at that point. x = -3 ONLY crosses the x -axis… at -3 y=5 ONLY crosses the y -axis… at 5

SUMMARY The formula for Standard Form is: Ax + By = C • If y=0, C ÷ A gives the x-intercept • If x=0, C ÷ B gives the y-intercept A • − — is the B slope Using the x-intercept and/or y-intercept as a starting point, you can use the slope to graph the line of the equation.
- Slides: 8