GRAPHING LINEAR EQUATIONS Beth Deacon Teacher Iowa State

GRAPHING LINEAR EQUATIONS Beth Deacon Teacher Iowa State Penitentiary Contact information: beth. deacon@iowa. gov 319 -372 -5432 ext. 41704

ALL THE FUN THINGS WE ARE LEARNING TODAY • What is a line? • Is the line going up or down? • How do you find the slope of a line? • What is the y-intercept of a line? • What is the x-intercept of a line? • What is slope-intercept form? • What does the graph of a quadratic equation look like? • By understanding the variables of an equation, you will now be able to eliminate answers on a test before actually graphing the equations.
TREND LINES
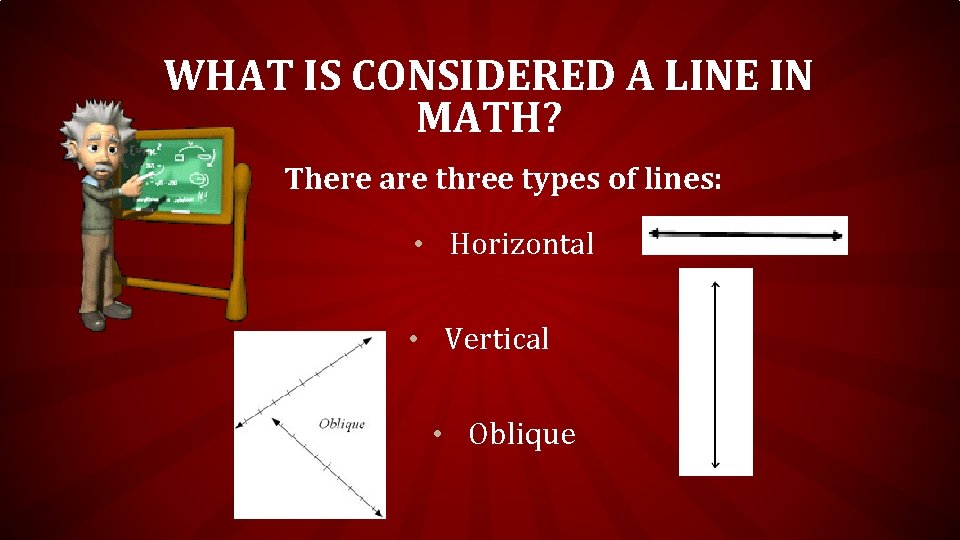
WHAT IS CONSIDERED A LINE IN MATH? There are three types of lines: • Horizontal • Vertical • Oblique
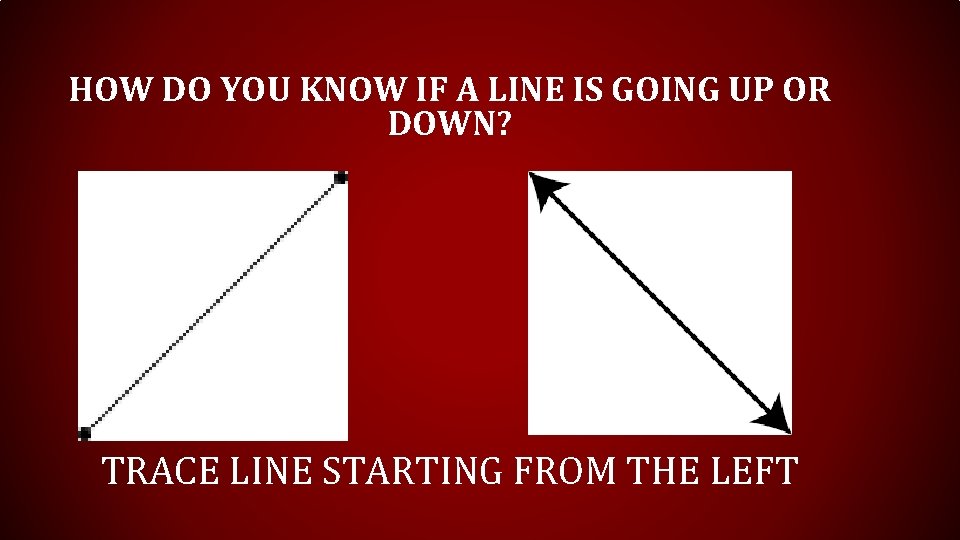
HOW DO YOU KNOW IF A LINE IS GOING UP OR DOWN? TRACE LINE STARTING FROM THE LEFT
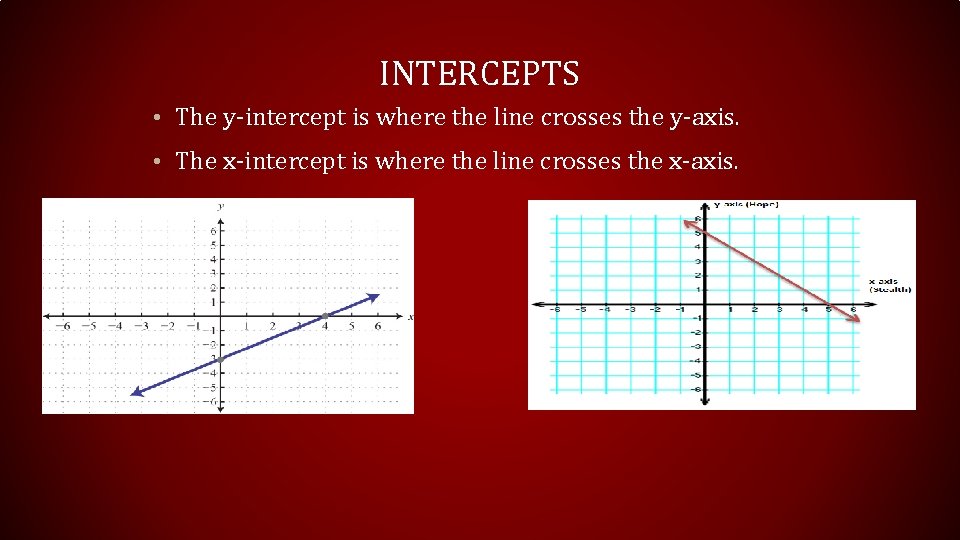
INTERCEPTS • The y-intercept is where the line crosses the y-axis. • The x-intercept is where the line crosses the x-axis.

TIME TO HIT THE SLOPES
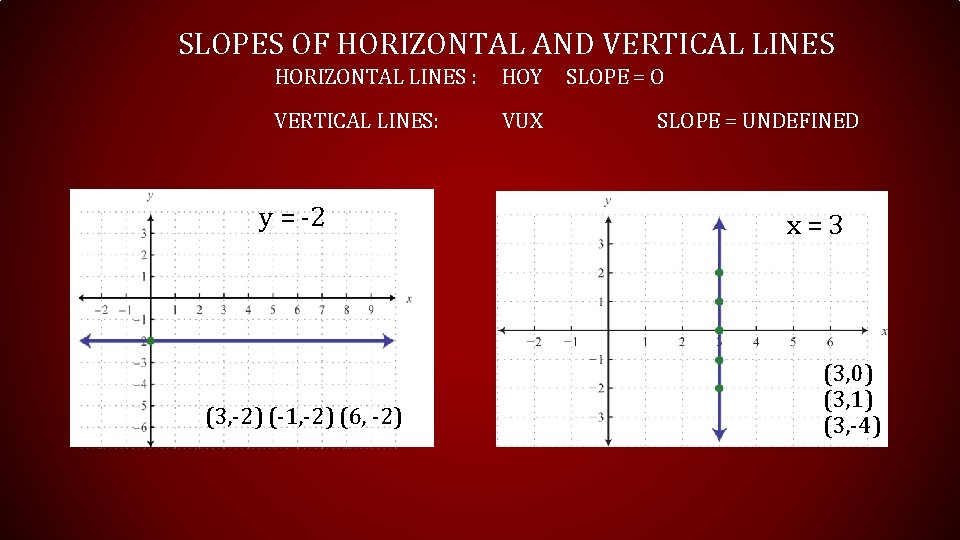
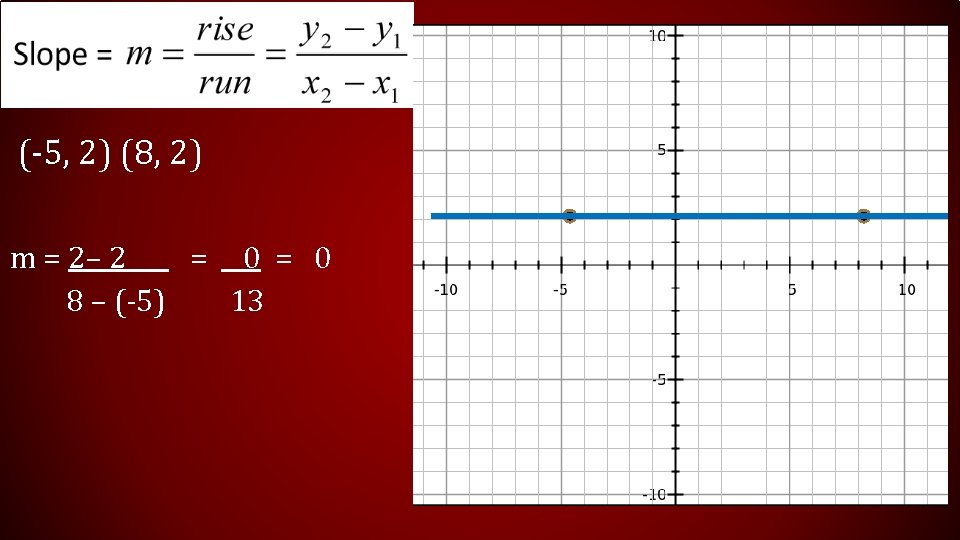
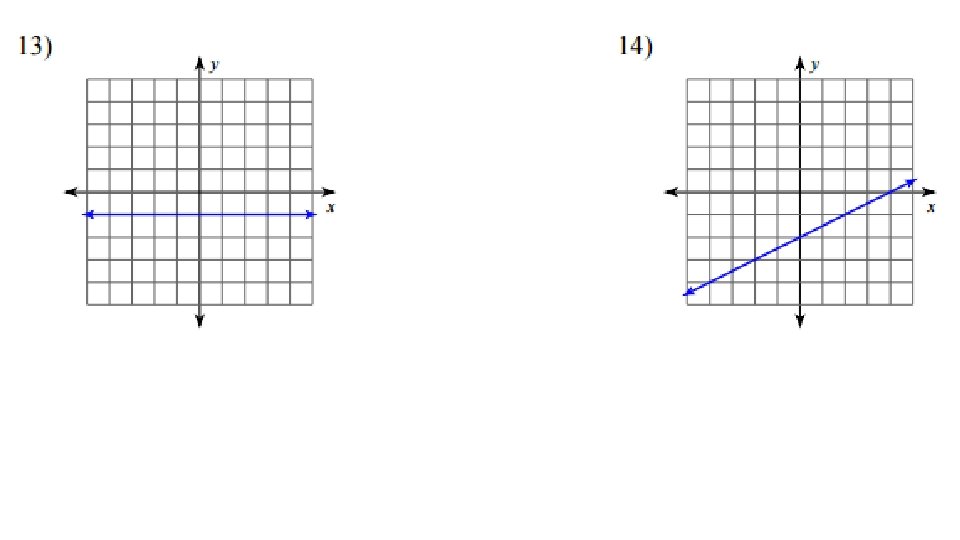
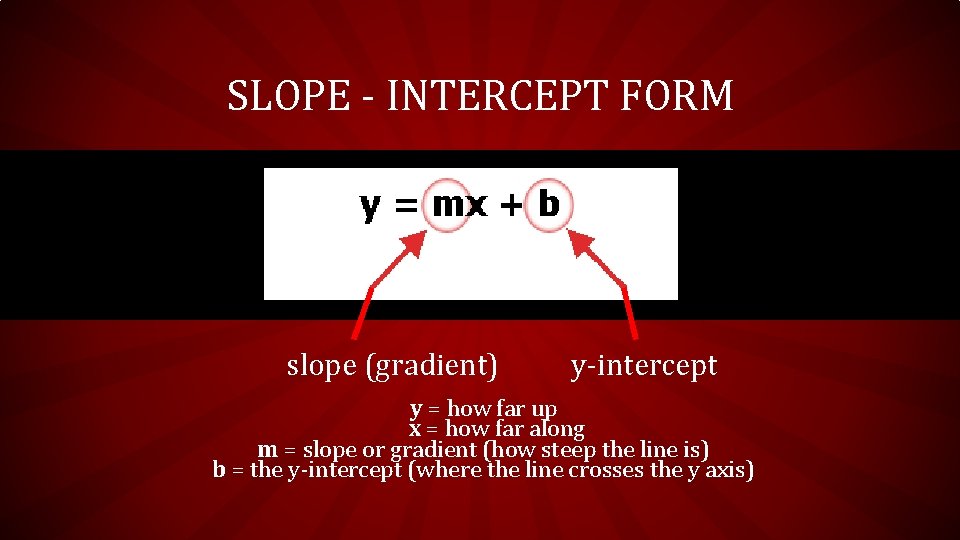
SLOPES OF HORIZONTAL AND VERTICAL LINES HORIZONTAL LINES : HOY SLOPE = O VERTICAL LINES: VUX y = -2 (3, -2) (-1, -2) (6, -2) SLOPE = UNDEFINED x = 3 (3, 0) (3, 1) (3, -4)
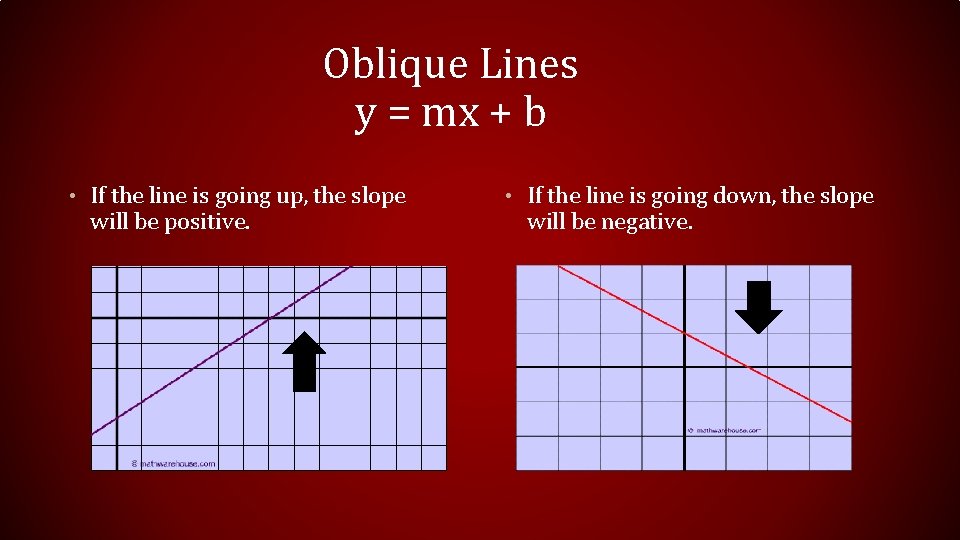
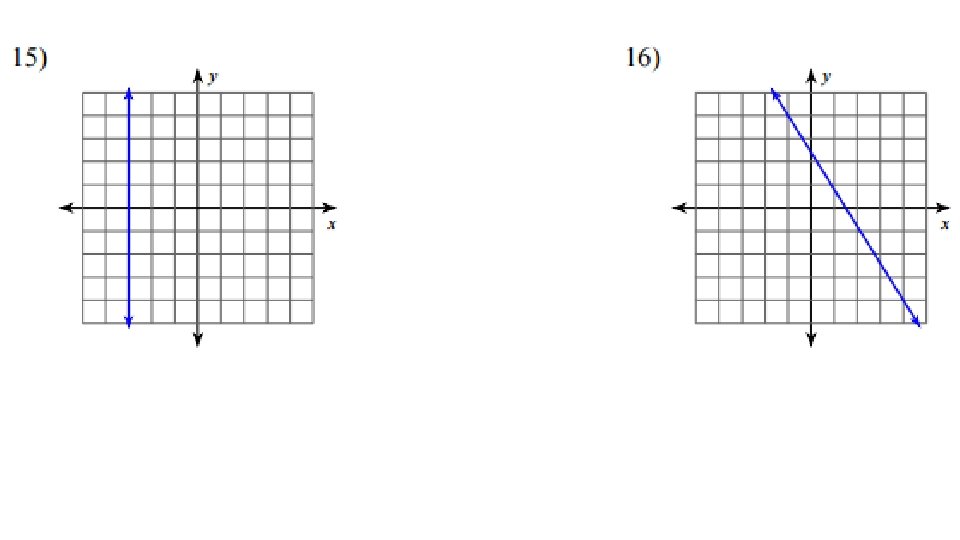
Oblique Lines y = mx + b • If the line is going up, the slope will be positive. • If the line is going down, the slope will be negative.
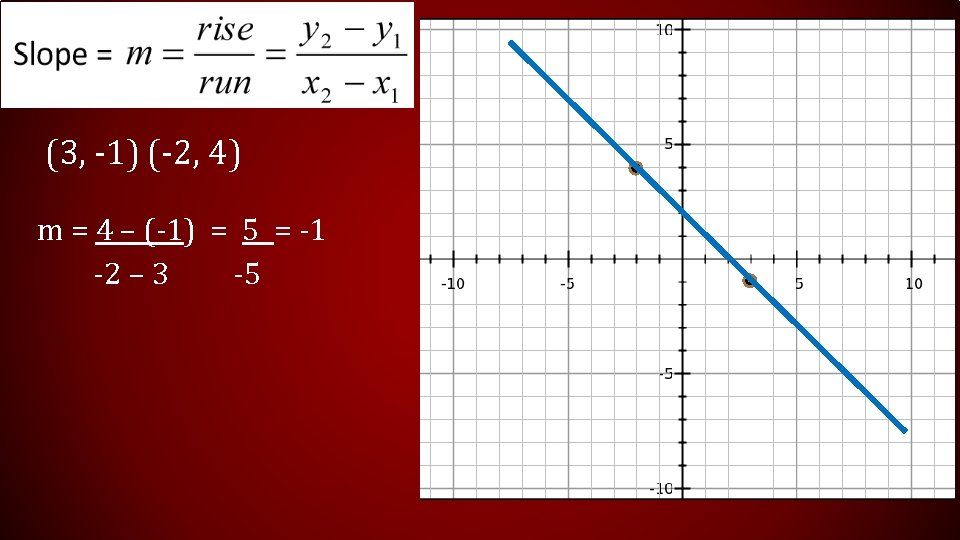
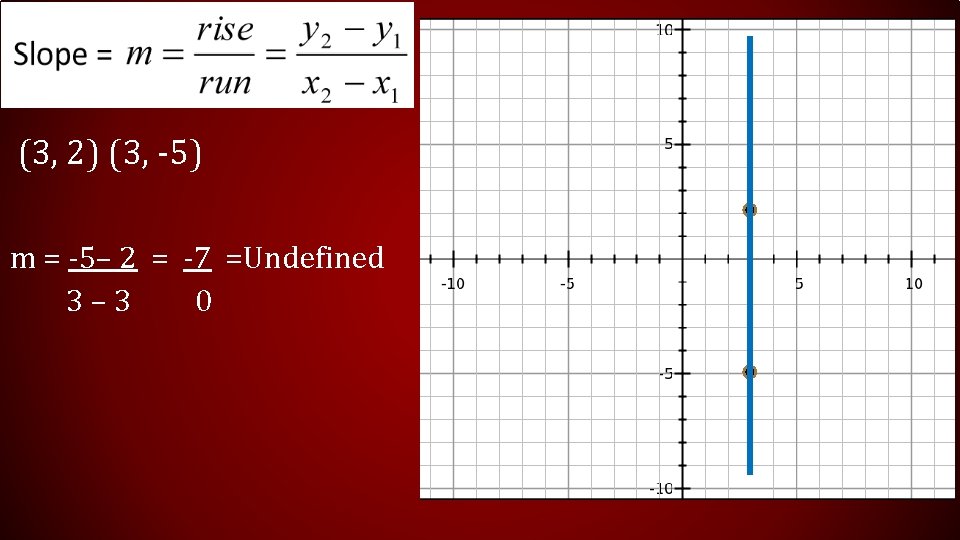
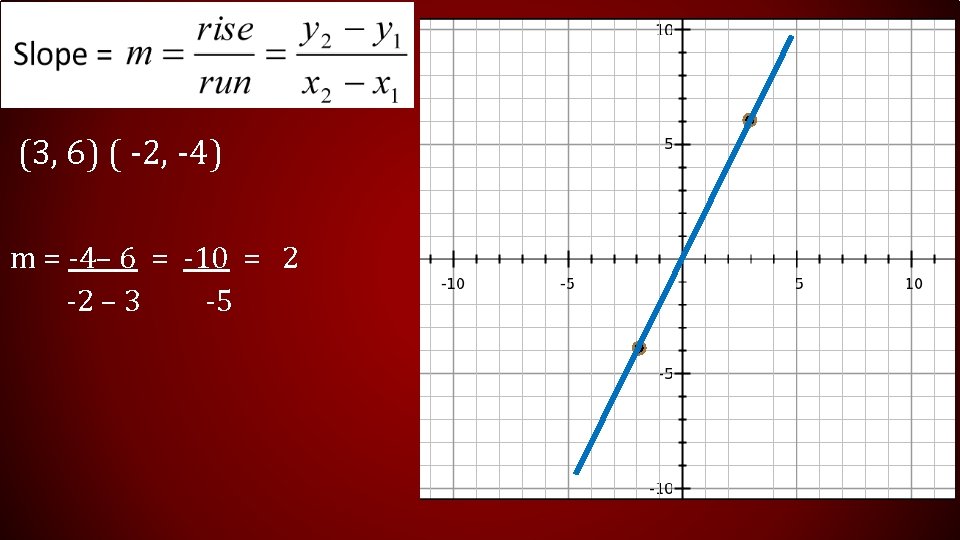
(3, 2) (3, -5) m = -5– 2 = -7 =Undefined 3 – 3 0
SLOPE - INTERCEPT FORM slope (gradient) y-intercept y = how far up x = how far along m = slope or gradient (how steep the line is) b = the y-intercept (where the line crosses the y axis)
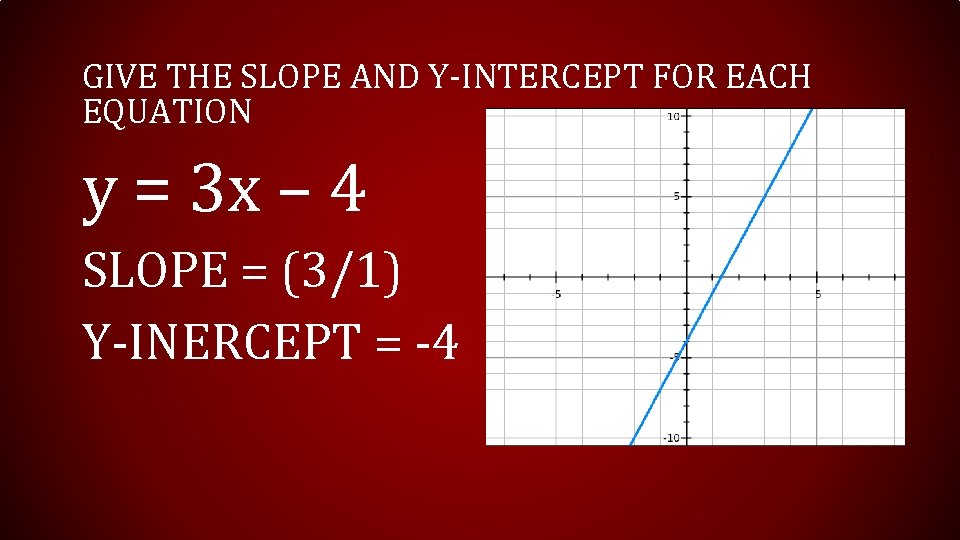
GIVE THE SLOPE AND Y-INTERCEPT FOR EACH EQUATION y = 3 x – 4 SLOPE = (3/1) Y-INERCEPT = -4
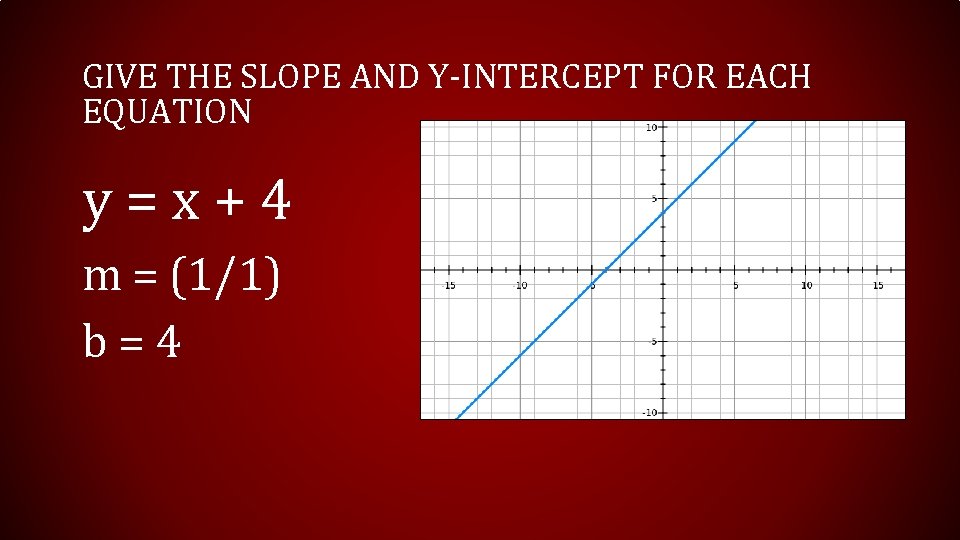
GIVE THE SLOPE AND Y-INTERCEPT FOR EACH EQUATION y = x + 4 m = (1/1) b = 4
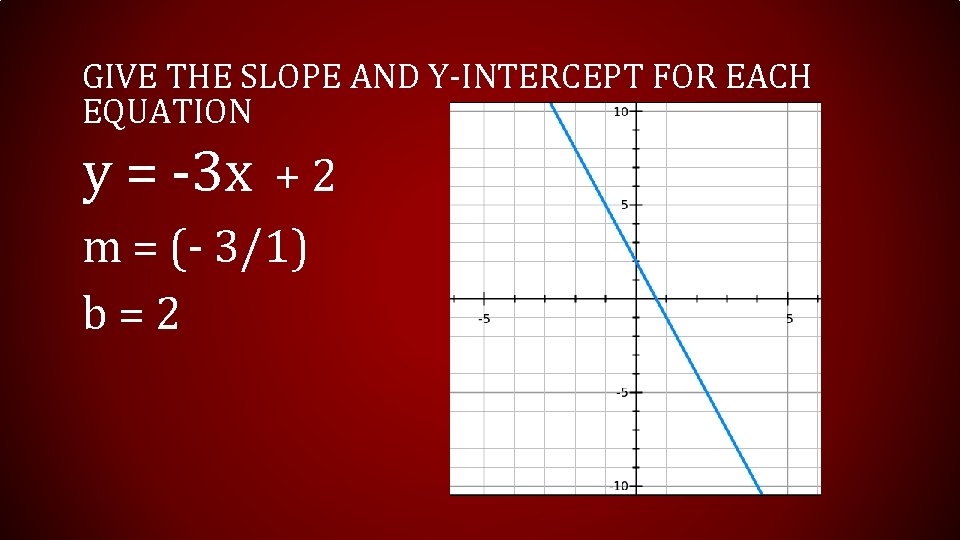
GIVE THE SLOPE AND Y-INTERCEPT FOR EACH EQUATION y = -3 x + 2 m = (- 3/1) b = 2
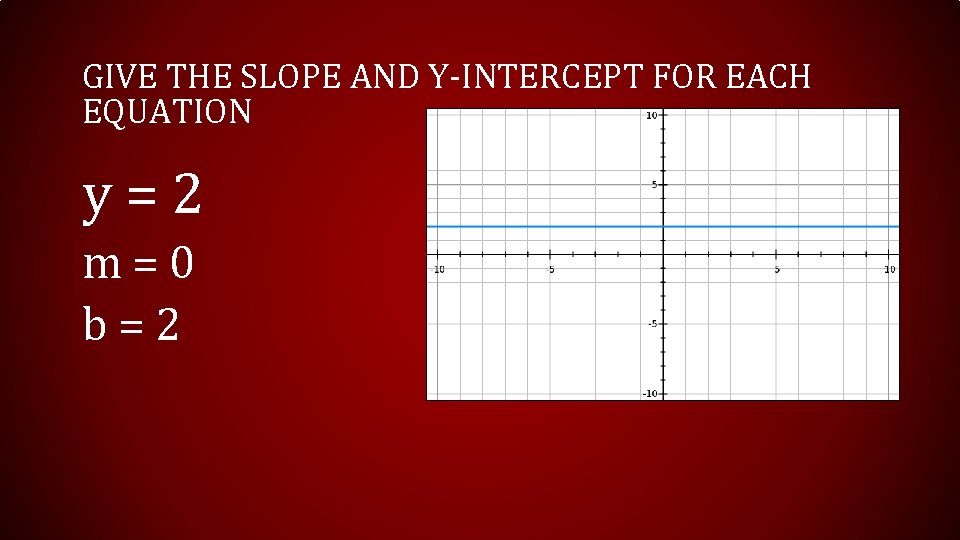
GIVE THE SLOPE AND Y-INTERCEPT FOR EACH EQUATION y = 2 m = 0 b = 2

GIVE THE SLOPE AND Y-INTERCEPT FOR EACH EQUATION x = -3 m = Undefined b = None
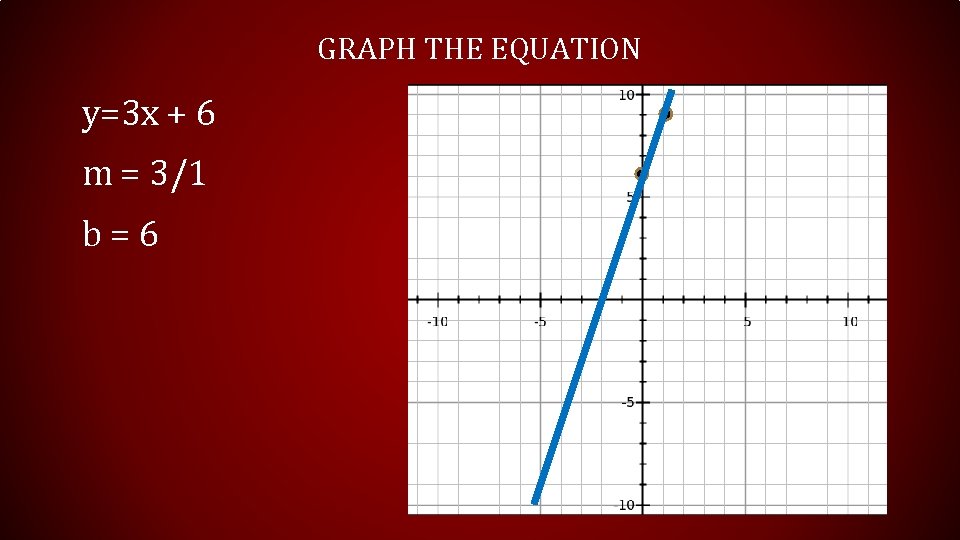
GRAPH THE EQUATION y=3 x + 6 m = 3/1 b = 6
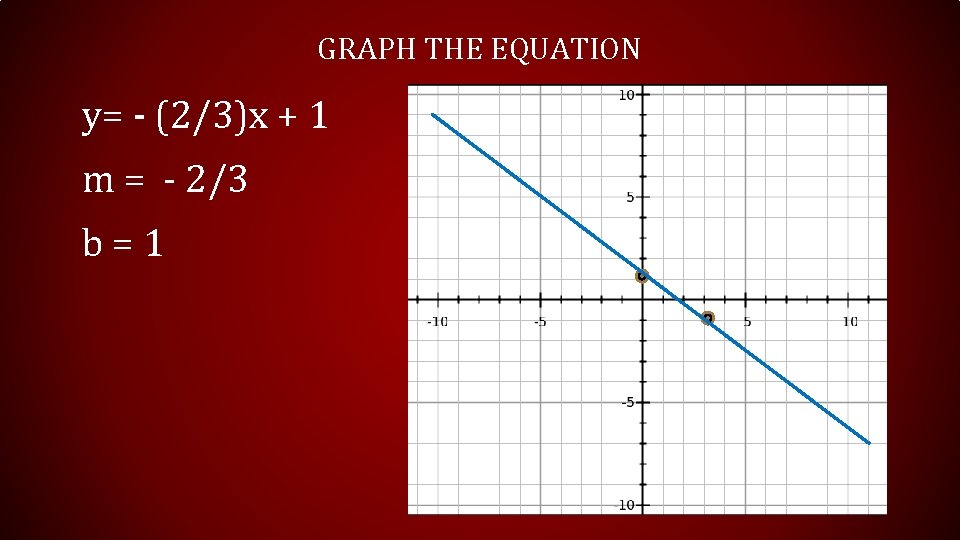
GRAPH THE EQUATION y= - (2/3)x + 1 m = - 2/3 b = 1
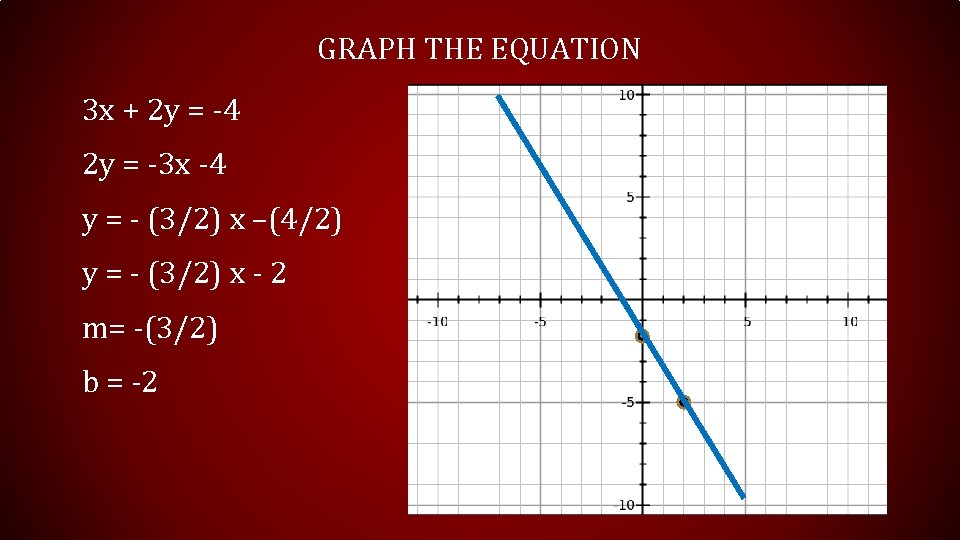
GRAPH THE EQUATION 3 x + 2 y = -4 2 y = -3 x -4 y = - (3/2) x –(4/2) y = - (3/2) x - 2 m= -(3/2) b = -2
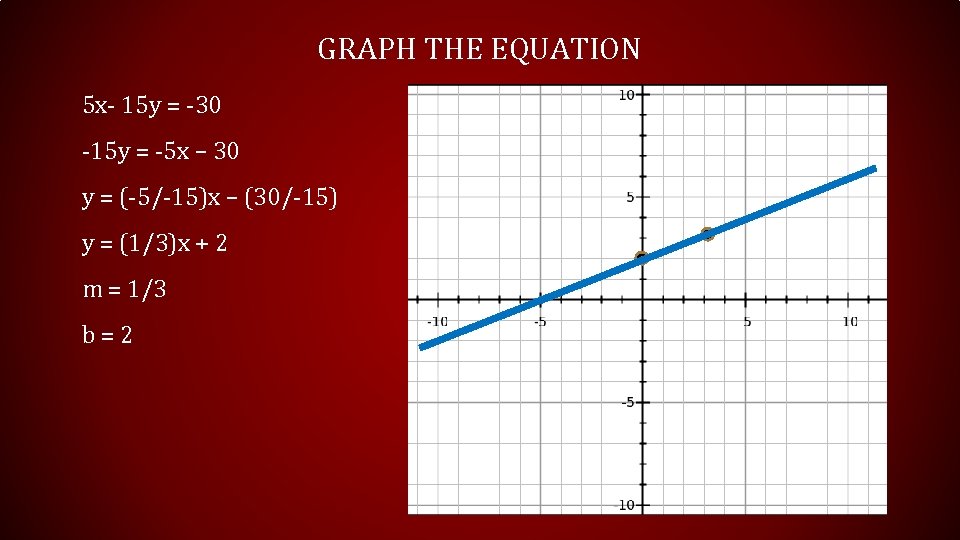
GRAPH THE EQUATION 5 x- 15 y = -30 -15 y = -5 x – 30 y = (-5/-15)x – (30/-15) y = (1/3)x + 2 m = 1/3 b = 2
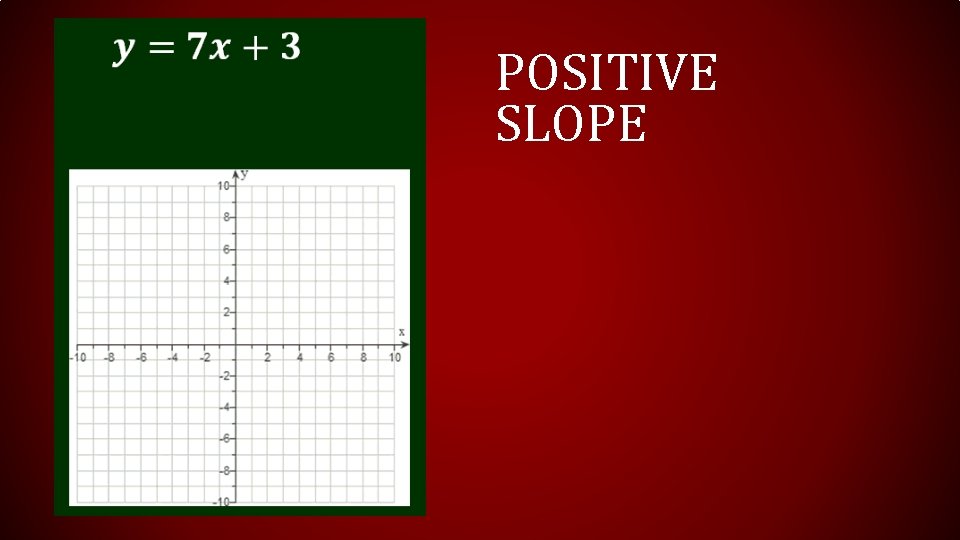
POSITIVE SLOPE
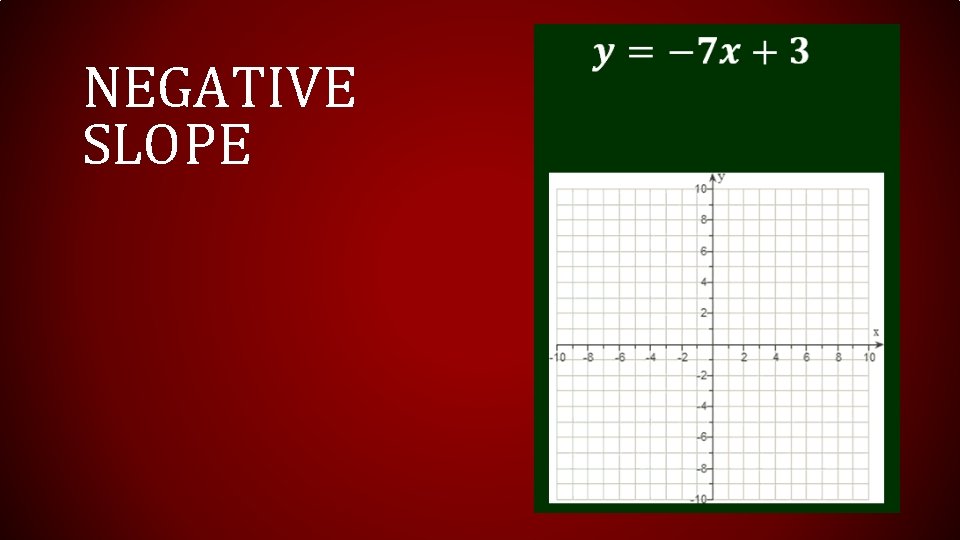
NEGATIVE SLOPE
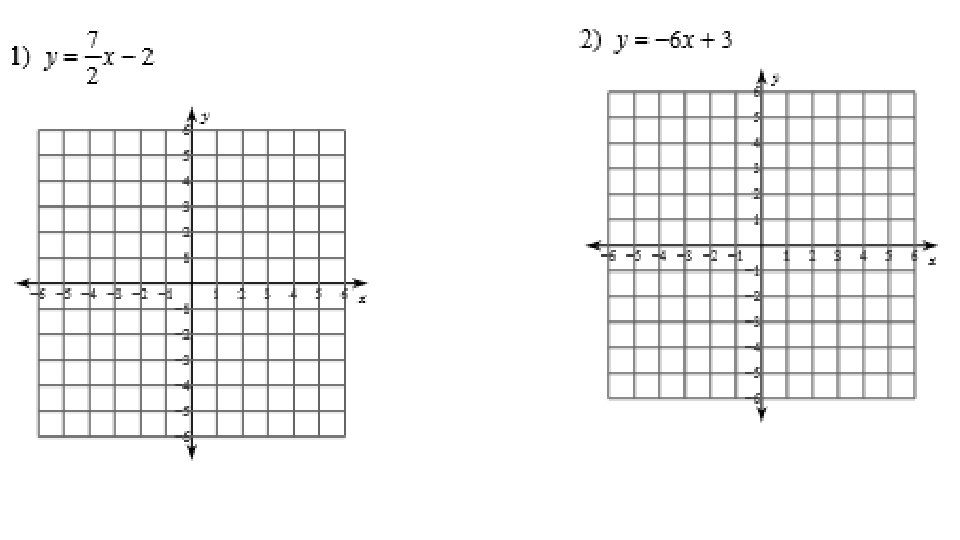
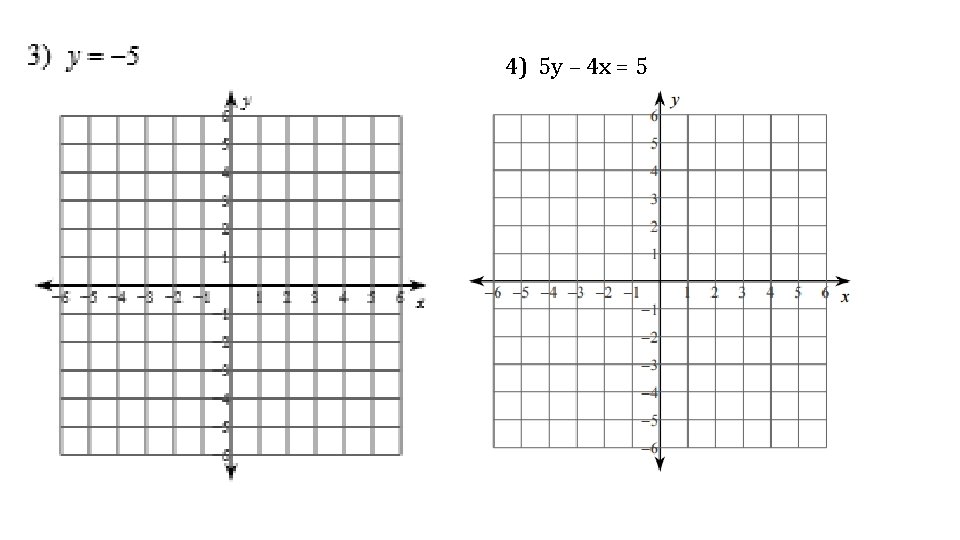
4) 5 y – 4 x = 5
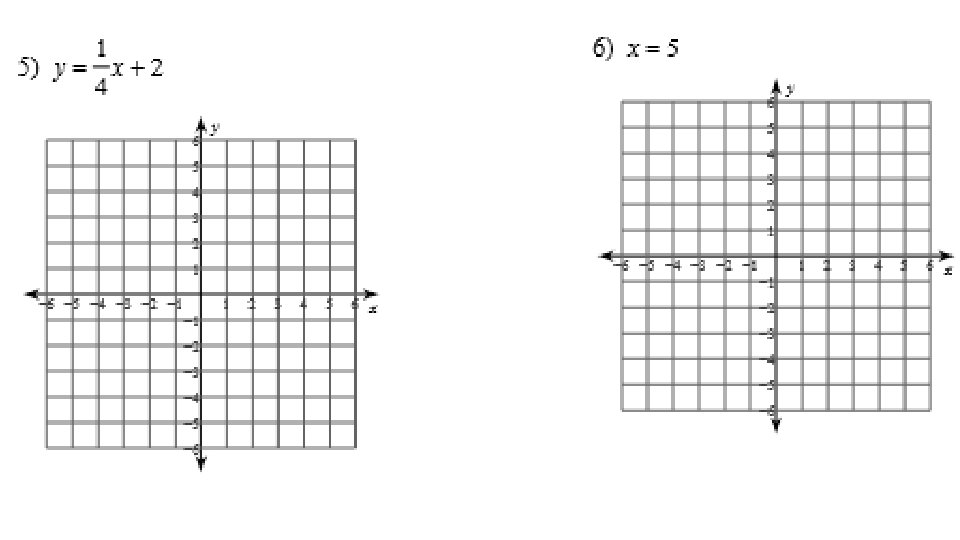


NOW YOU CAN GRAPH A LINE ISN’T THAT COOL?

Math is like a gym for your brain. You may never need to use the quadratic equation in your adult life, but the process of learning it boosts your brainpower.

In algebra, a quadratic equation (from the Latin quadratus for "square") is any equation having the form: 2 y = ax + bx + c

We are studying parabolas in standard form. y = ax 2 + bx + c For parabolas of the form : x = ay 2 + by + c The parabolas open to the right for positive “a” values and to the left for negative “a” values.
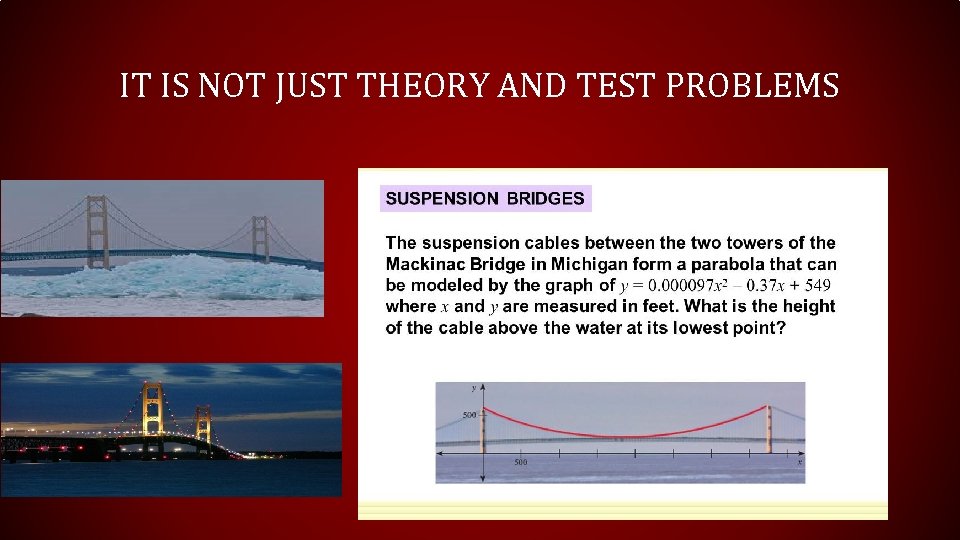
IT IS NOT JUST THEORY AND TEST PROBLEMS
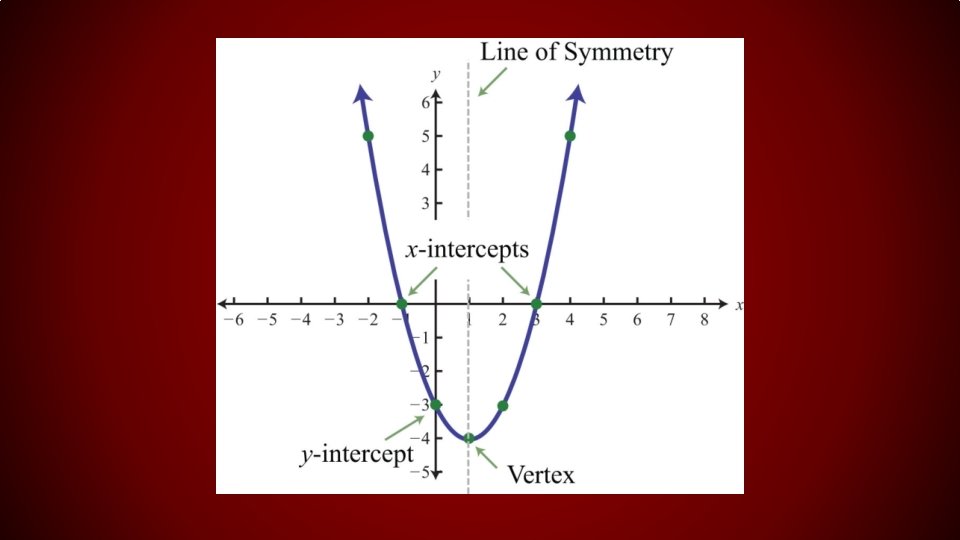

RULES FOR GRAPHING PARABOLAS • y = ax 2 + bx + c • A positive “a” means the graph opens up • A negative “-a” means the graph opens down • As the value of “a” increases, the graph gets narrower • ‘”c” tells us where the graph crosses the y axis
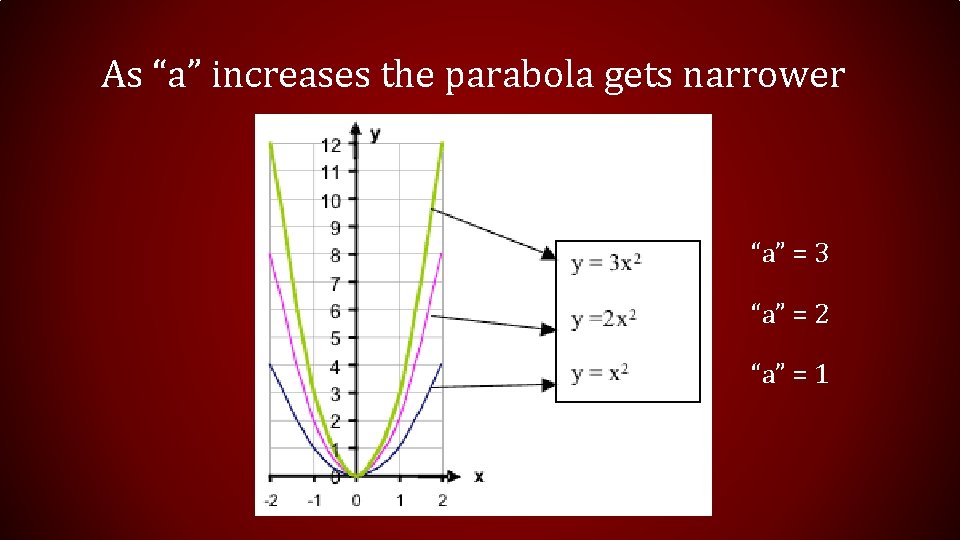
As “a” increases the parabola gets narrower “a” = 3 “a” = 2 “a” = 1
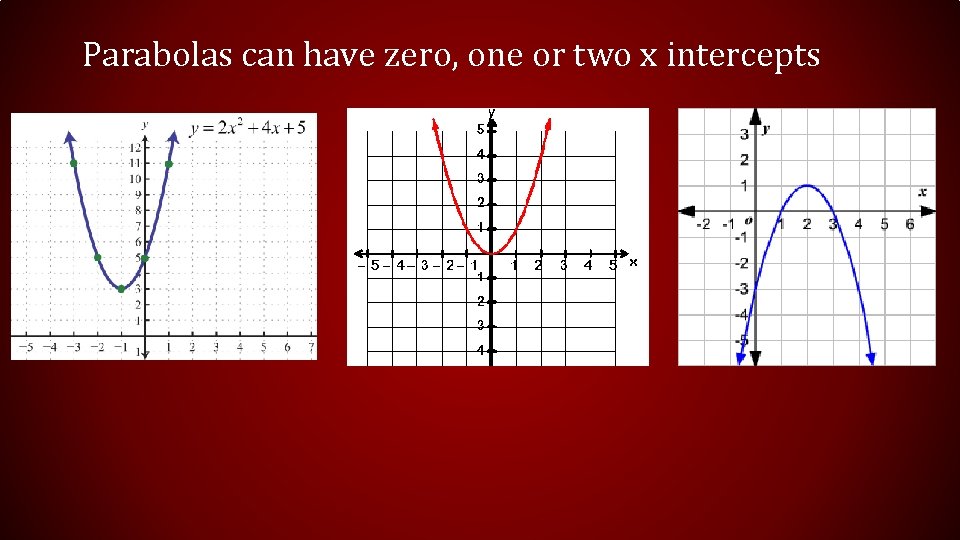
Parabolas can have zero, one or two x intercepts
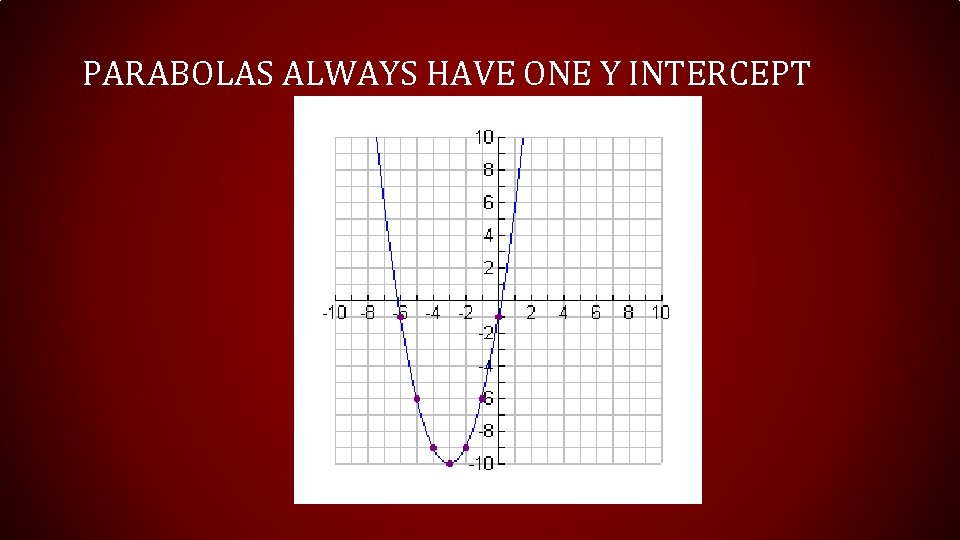
PARABOLAS ALWAYS HAVE ONE Y INTERCEPT
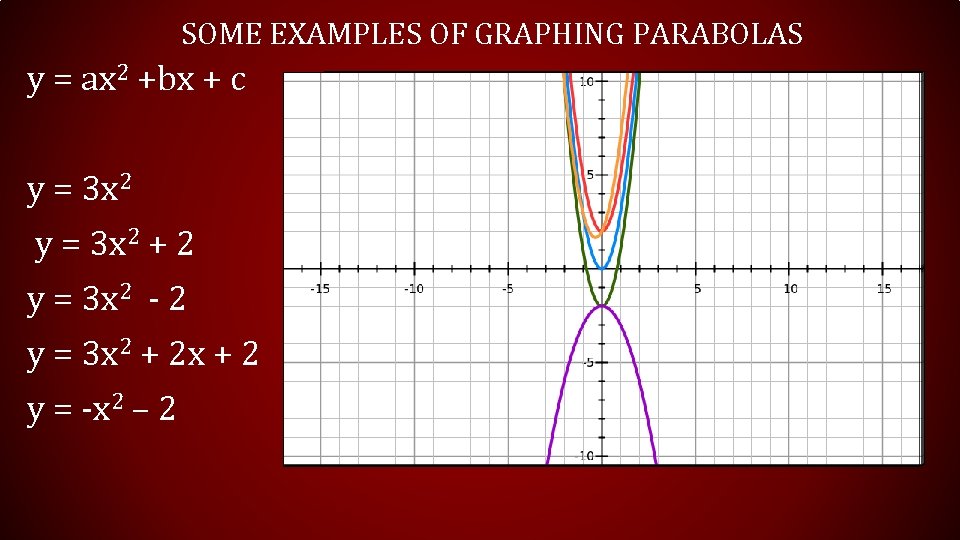
SOME EXAMPLES OF GRAPHING PARABOLAS y = ax 2 +bx + c y = 3 x 2 + 2 y = 3 x 2 - 2 y = 3 x 2 + 2 x + 2 y = -x 2 – 2

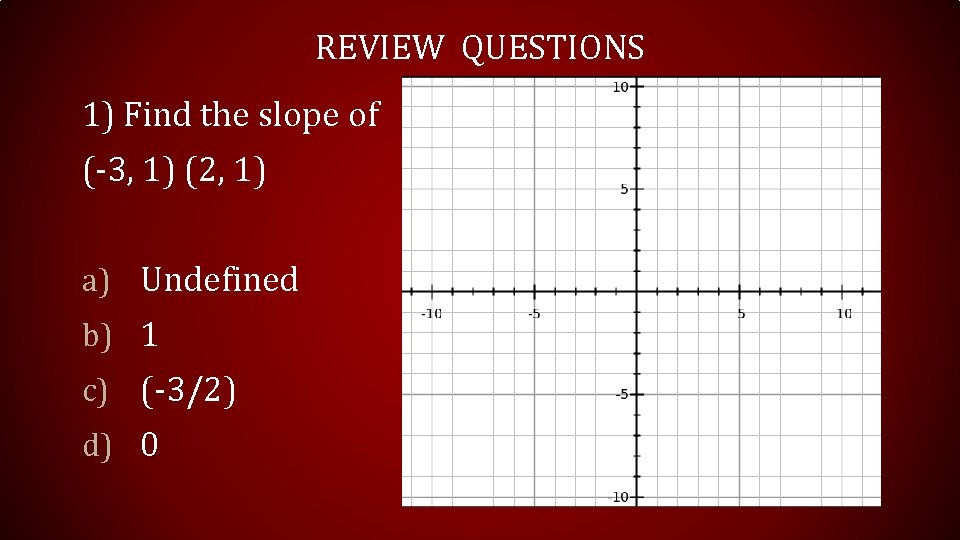
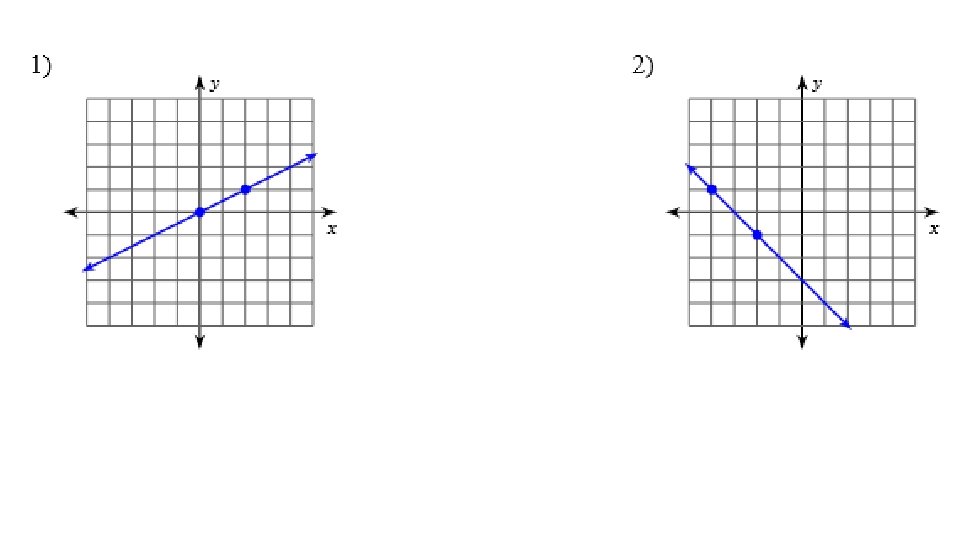
REVIEW QUESTIONS 1) Find the slope of (-3, 1) (2, 1) a) Undefined b) 1 c) (-3/2) d) 0
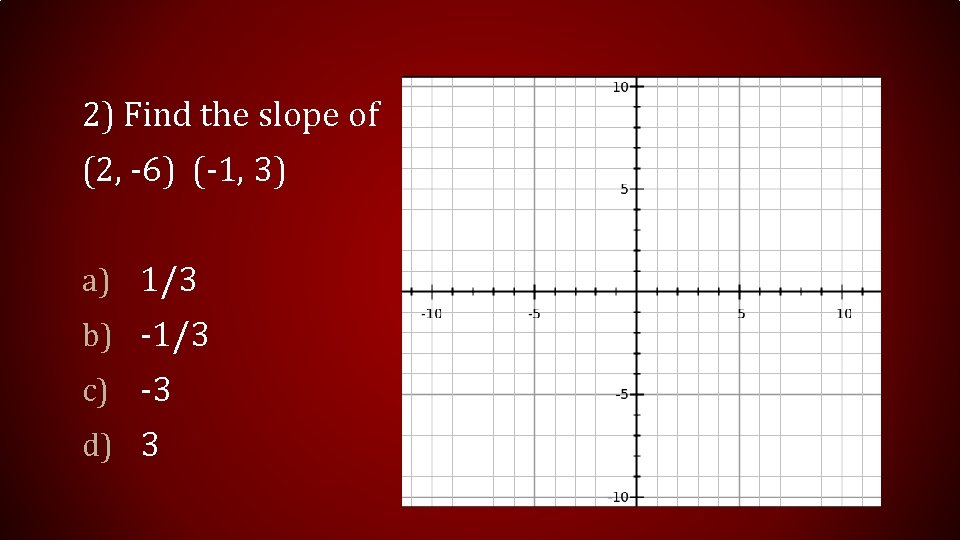
2) Find the slope of (2, -6) (-1, 3) a) 1/3 b) -1/3 c) -3 d) 3
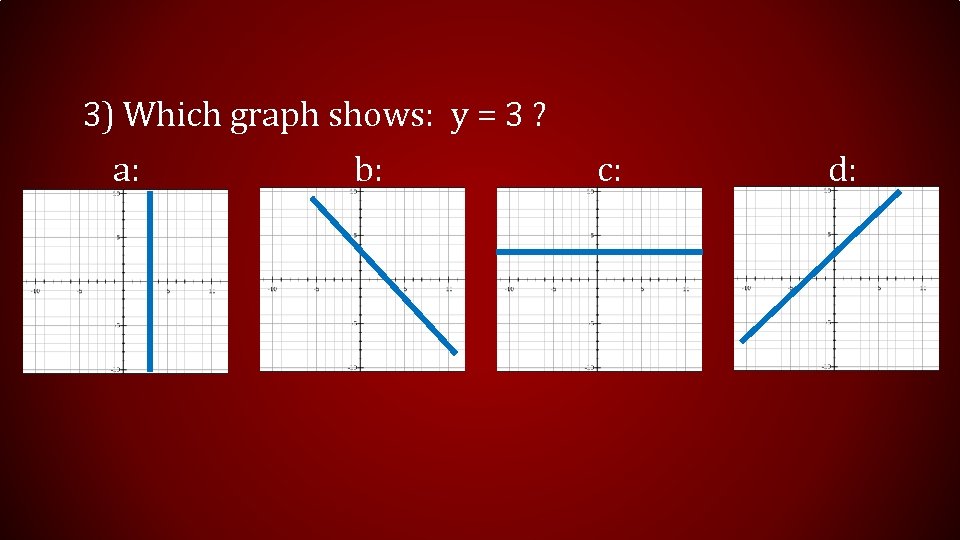
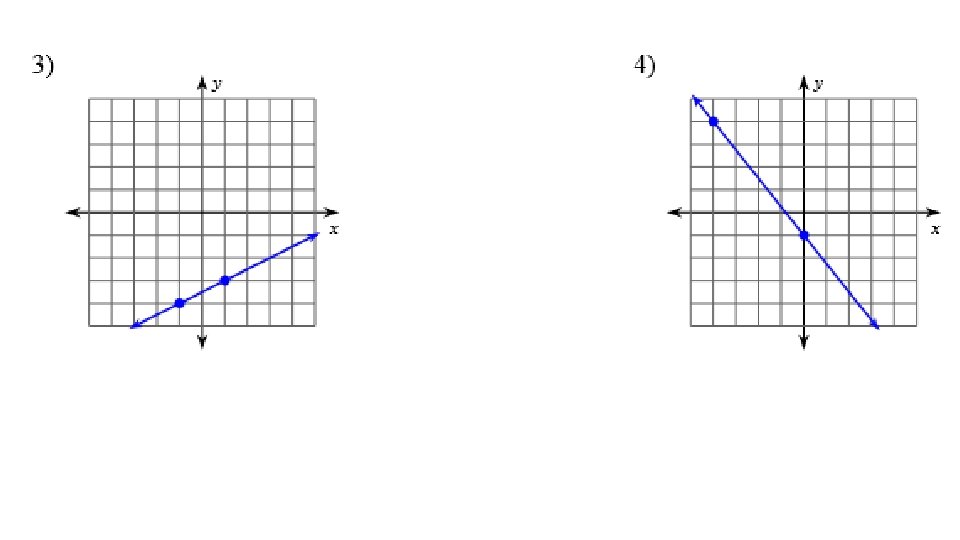
3) Which graph shows: y = 3 ? a: b: c: d:
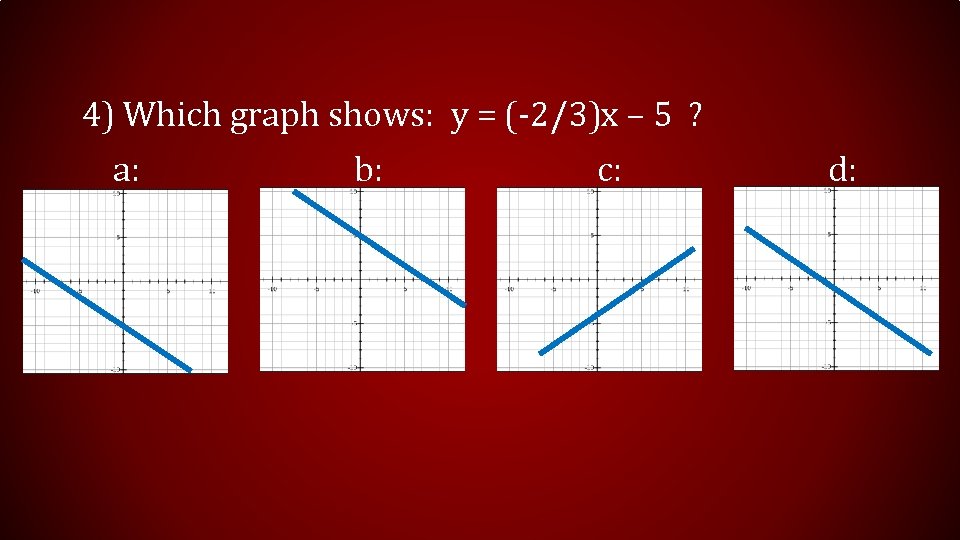
4) Which graph shows: y = (-2/3)x – 5 ? a: b: c: d:
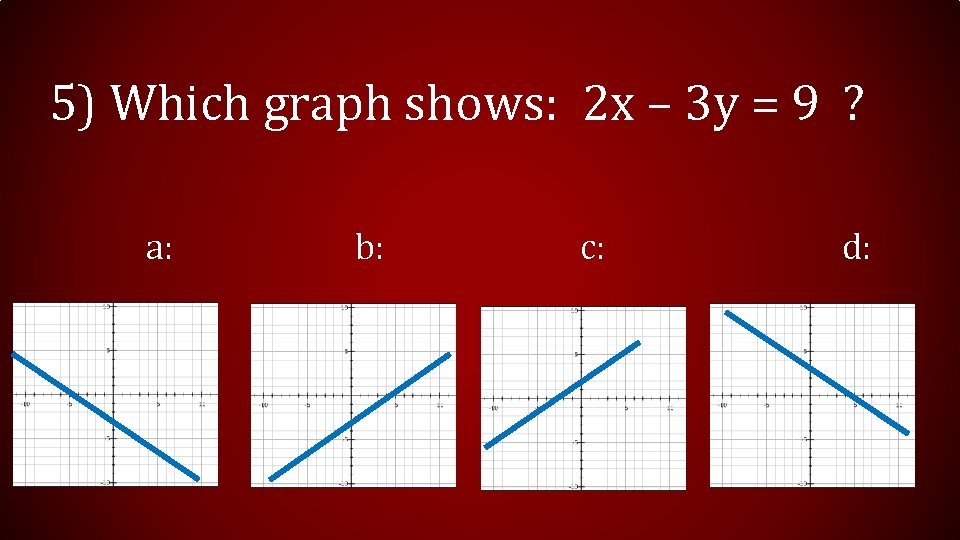
5) Which graph shows: 2 x – 3 y = 9 ? a: b: c: d:
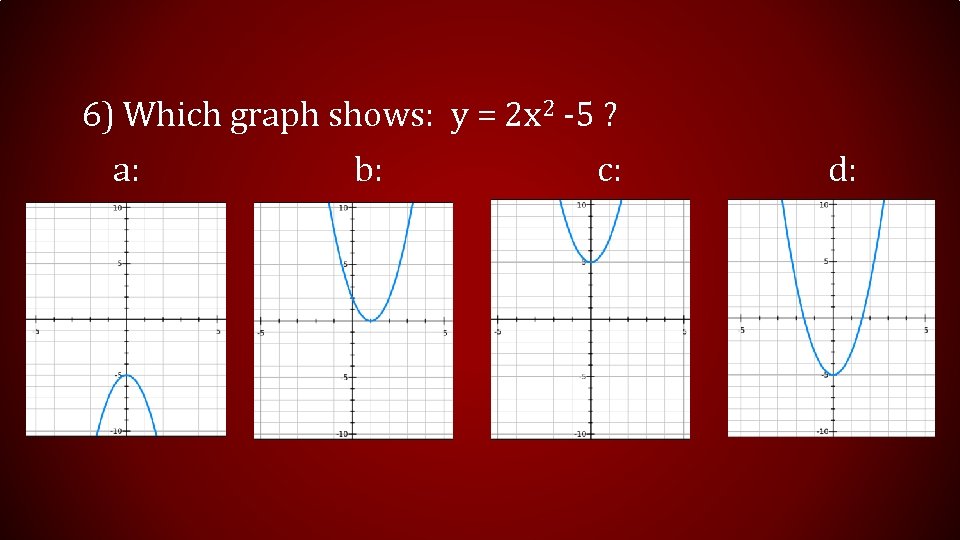
6) Which graph shows: y = 2 x 2 -5 ? a: b: c: d:
7) Which graph is wider: y = 3 x 2 or y = -3 x 2 a) y = 3 x 2 b) y = -3 x 2 c) They are equal d) All of the above

8) Will the graph of y = 2 x 2 + 3 x + 1 have a minimum or maximum for the vertex? a) minimum b) maximum c) both d) neither

9) How do you know if a line is going up or down?

10) Last question. Have you learned anything today?

Thank you for your attention Beth Deacon
- Slides: 57