Graphing Linear Equations 1 Equations tables of values

Graphing Linear Equations 1

Equations, tables of values, and graphs can all be used to describe a relationship between unknown values. Which ones we use depends on what we are given, and what our goals are. [Or of course, what the instructions tell us we must do to score points. ] Lets explore one relationship using each method of display. 2

Your Mom is pulling out all the stops in an effort to get you to work to your full potential in school. She offers you a deal. She will give you $20 if you have at least a B average for the first marking period, plus an extra $5 for every A you earn. Let’s assume that you are willing to put forth the effort (because that is all it really takes!) and you do have an average of at least a B. We can figure out how much money you can pocket each marking period. 3

� First we should define our unknowns (declare our variables) y = The amount of money earned x = The number of A’s earned � We can write a word-equation describing the situation to guide ourselves into the actual equation The amount of money earned = $20 for the average + $5 for each A � Lastly we can translate the situation into an algebraic equation. y = 20 + 5 x Or , to make it fit into slope intercept form… y = 5 x + 20 4

� The table of values can be created if given the relationship, the graph, or the equation. � The table will only represent a selection of possible ‘solutions’. x y 0 20 1 25 2 30 � If you have a hard time creating an equation, you can fill a table of values first in an attempt to better see the relationship. � You could then use that table of values to draw the graph, and use the graph to find the equation 5
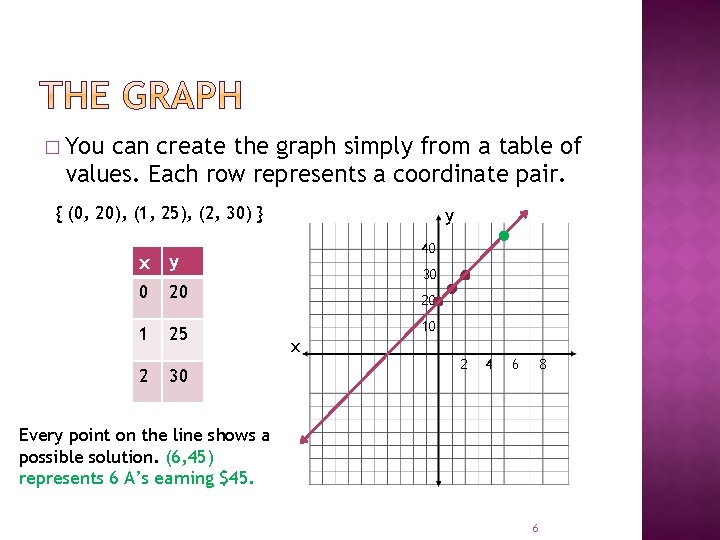
� You can create the graph simply from a table of values. Each row represents a coordinate pair. { (0, 20), (1, 25), (2, 30) } x y 0 20 1 25 2 30 y 40 30 20 10 x 2 4 6 8 Every point on the line shows a possible solution. (6, 45) represents 6 A’s earning $45. 6

� The slope of the line is a measurement that describes the steepness of a line. �If the line slants down from left to right the slope is negative § If the line slants up from left to right the slope is positive. § The closer the slope is to zero, the closer the line is to horizontal. [horizontal lines have a slope of 0] § The closer the slope gets to ±∞, the closer the line is to vertical. [vertical lines have an undefined slope] 7

� The y-intercept is the value of y when x=0. The y-intercept is the value of y when the line crosses the y-axis. The y-intercept is the ‘b’ in slope intercept form ( y = mx + b) � The y-intercept. x-intercept The x-intercept is the value of x when y=0. The x-intercept is the value of x when the line crosses the y-axis. The time we most often find the x-intercept is when we want to graph but are given an equation that is not easily transformed into slope intercept form. 8

� Slope can be identified from an equation only when the y variable is alone on one side of the equation. When y is alone, the slope is the coefficient of the x variable. y = 5 x + 2 Slope = 5 5 -2 x = y Slope = -2 � When the y variable is alone on one side of the equation, the y-intercept is the constant on the other side. y = -3 x + 2 y-int = 2 y = 5 x y-int = 0 9

� The y-intercept can always be found by setting x=0 and solving for y. 3 x + 9 y = 54 y-intercept : set x = 0 3(0)+9 y = 54 y-intercept at (0, 6) y=6 � The x-intercept can always be found by setting y=0 and solving for x. 3 x + 9 y = 54 x-intercept : set y = 0 3 x + 9(0) = 54 3 x = 54 x = 18 x-intercept at (18, 0) 10

� In a table of values, the y-intercept is the value of y where x=0. � In a table of values, the x-intercept is the value of x where y=0. � If you cant find these values you could use the data to write an equation and calculate the intercepts. X Y 18 0 3 5 0 6 -6 8 x-intercept @ (18, 0) y-intercept @ (0, 6) 11
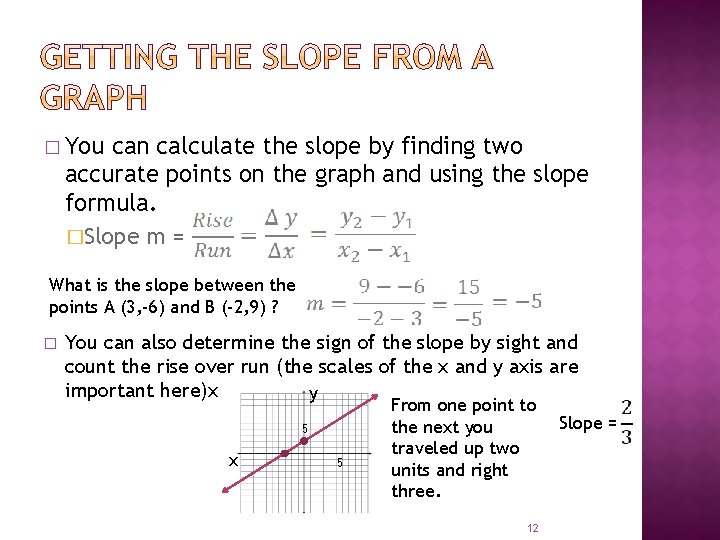
� You can calculate the slope by finding two accurate points on the graph and using the slope formula. �Slope m = What is the slope between the points A (3, -6) and B (-2, 9) ? � You can also determine the sign of the slope by sight and count the rise over run (the scales of the x and y axis are important here)x y 5 x 5 From one point to the next you traveled up two units and right three. 12 Slope =
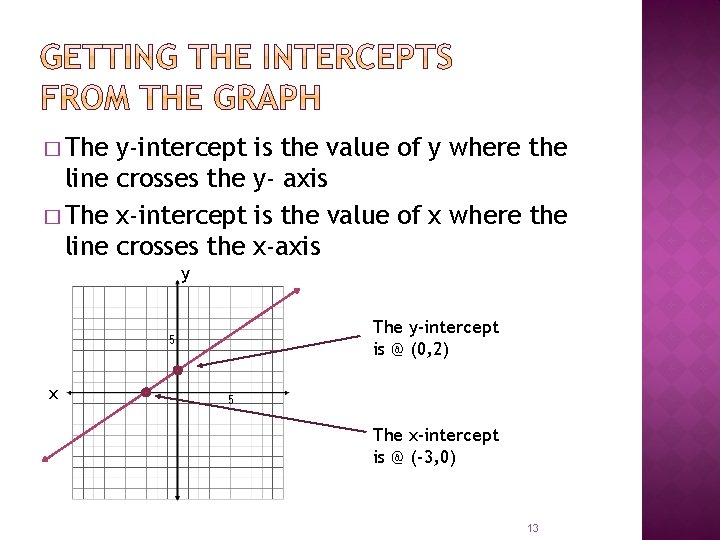
� The y-intercept is the value of y where the line crosses the y- axis � The x-intercept is the value of x where the line crosses the x-axis y The y-intercept is @ (0, 2) 5 x 5 The x-intercept is @ (-3, 0) 13

� Given the following situation, create an equation. Using that equation create a table of values. Using the equation or the table of values to sketch the graph of the relationship. � Markies Bakery Charges $20 for the first 12 cupcakes in a special order. They then charge $0. 75 for each additional cupcake. How much money might someone pay for their specialty cupcakes? 14

� Declare y = The total cost of the cupcake order x = The additional cupcakes (after the first 12) � Write the variables. a sentence describing the relationship. The cost of the cupcake order = $20 for the first 12 and $0. 75 per additional cupcake � Translate the sentence into an algebraic equation. y = 20 +0. 75 x Or …. 15

Our equation X Y -4 17 0 20 4 23 8 26 If possible, choose x values that will work easily with the equation. 16
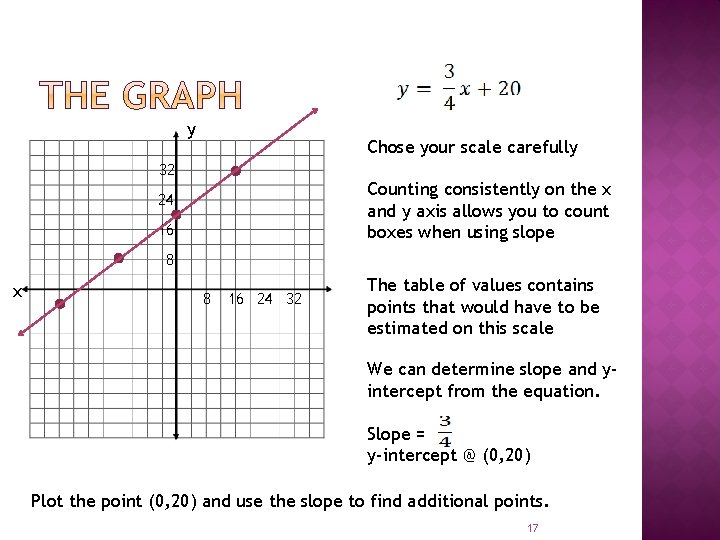
y Chose your scale carefully 32 Counting consistently on the x and y axis allows you to count boxes when using slope 24 16 8 x 8 16 24 32 The table of values contains points that would have to be estimated on this scale We can determine slope and yintercept from the equation. Slope = y-intercept @ (0, 20) Plot the point (0, 20) and use the slope to find additional points. 17
- Slides: 17