Graphing Exponential Functions Discovery Activity using TISmart View

Graphing Exponential Functions • Discovery Activity using TI-Smart. View or Applet • How is the equation of an exponential function similar to that of the Quadratic and Absolute Value Functions? (slides 3 - 8) • Check for Understanding : Partners Assignment (slide 9)

Discovery Activity • Working with a neighbor, follow directions on the handout. • Students take turns coming to the computer to graph each exponential function using the TI-Smart. View or Applet. • As a class, identify points you see on the graph that could be plotted on your paper to graph each function by hand. • Fill in the appropriate blanks next to each graph. • Continue to each graph until all graphs are complete. • Answer the following questions at the bottom of your paper amongst your pairs. • 10 minute group discussion to determine what was found.

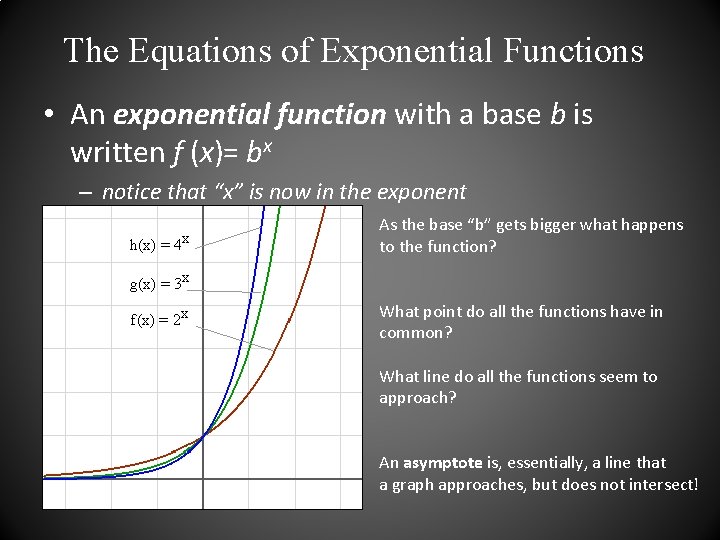
The Equations of Exponential Functions • An exponential function with a base b is written f (x)= bx – notice that “x” is now in the exponent As the base “b” gets bigger what happens to the function? What point do all the functions have in common? What line do all the functions seem to approach? An asymptote is, essentially, a line that a graph approaches, but does not intersect!

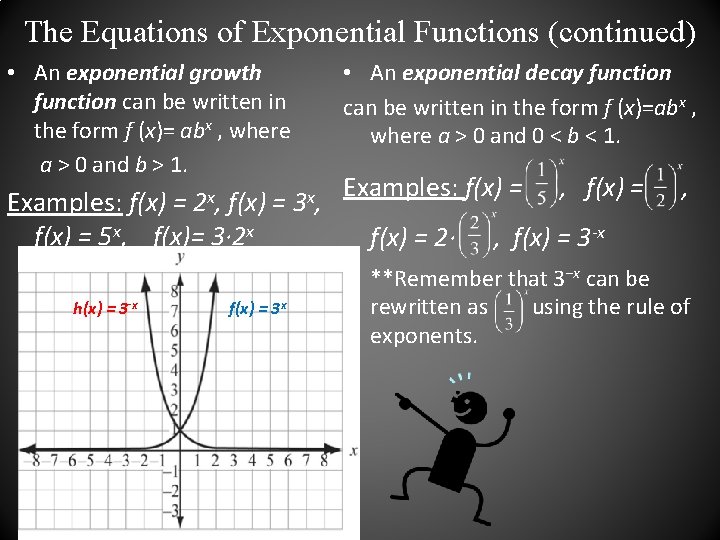
The Equations of Exponential Functions (continued) • An exponential growth function can be written in the form f (x)= abx , where a > 0 and b > 1. 2 x, Examples: f(x) = 5 x, f(x)= 3∙ 2 x h(x) = 3 -x f(x) = 3 x • An exponential decay function can be written in the form f (x)=abx , where a > 0 and 0 < b < 1. 3 x, Examples: f(x) = 2∙ , f(x) = , , f(x) = 3 -x • **Remember that 3−x can be rewritten as using the rule of exponents.

The Equations of Exponential Functions (continued 2) • Transformations can be applied to exponential functions when written in the form: f (x)= abx−h +k Look familiar? ? Quadratic Function: f(x) = a(x-h) + k The “a”, “h”, and “k” Absolute Value Function: f(x) = a|x-h| + k transform the graph of an exponential function in the same manner! 2

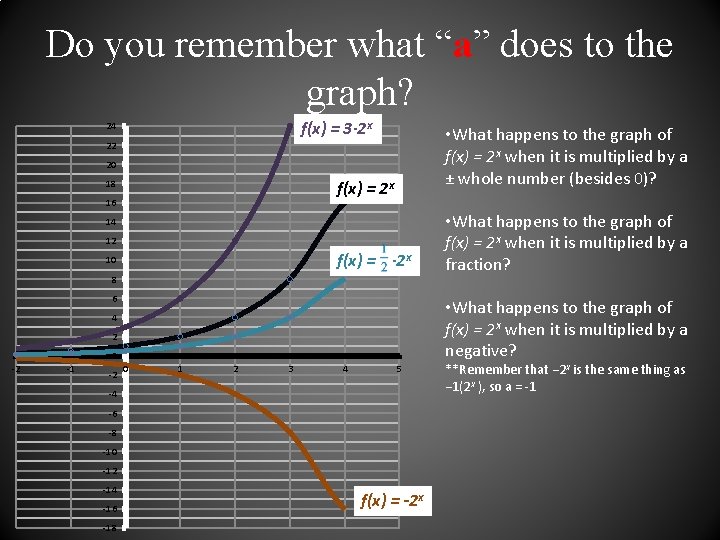
Do you remember what “a” does to the graph? f(x) = 3∙ 2 x 24 22 • What happens to the graph of f(x) = 2 x when it is multiplied by a ± whole number (besides 0)? 20 18 f(x) = 2 x 16 14 12 f(x) = ∙ 2 x 10 8 6 • What happens to the graph of f(x) = 2 x when it is multiplied by a negative? 4 2 0 -2 -1 -2 0 1 2 3 4 5 -4 -6 -8 -10 -12 -14 -16 -18 • What happens to the graph of f(x) = 2 x when it is multiplied by a fraction? f(x) = -2 x **Remember that − 2 x is the same thing as − 1(2 x ), so a = -1

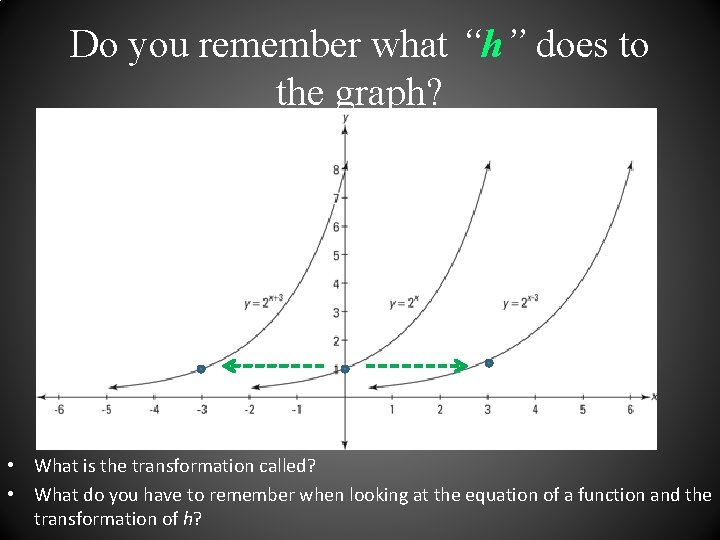
Do you remember what “h” does to the graph? • What is the transformation called? • What do you have to remember when looking at the equation of a function and the transformation of h?

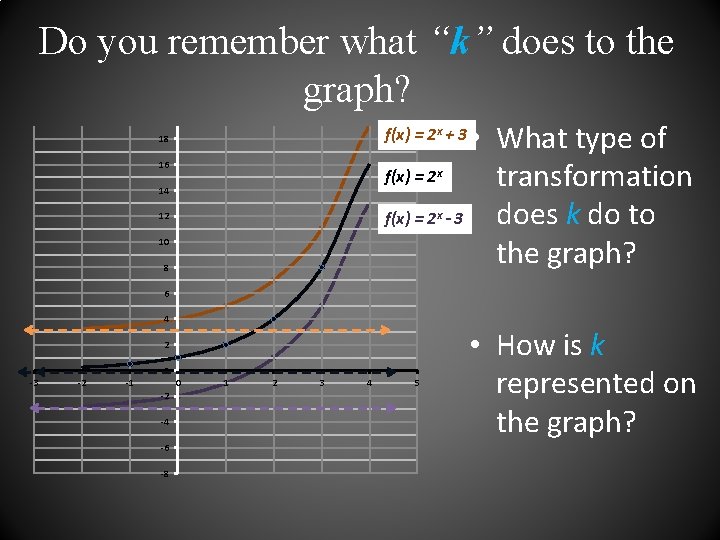
Do you remember what “k” does to the graph? • What type of f(x) = 2 transformation does k do to f(x) = 2 - 3 the graph? f(x) = 2 x + 3 18 16 x 14 x 12 10 8 6 4 2 0 -3 -2 -1 0 -2 -4 -6 -8 1 2 3 4 5 • How is k represented on the graph?

You can always make a table to graph functions! • Describe the transformations for the graph of each function below. • Then, use a table to graph the function and verify that the transformations you predicted are indeed what has occurred. f(x) = 2 x-1 – 4 g(x) = -2∙ Give the domain, range, asymptote(s), intervals of decrease/increase, and intercept(s).

Homework • Create an exponential function with at least three transformations. • Include: – equation – description of the transformations – a graph of the function – domain, range, asymptote(s), intervals of decrease/increase, and intercept(s).