Graphing Complex Numbers AND Finding the Absolute Value

Graphing Complex Numbers AND Finding the Absolute Value of Complex Numbers SPI 3103. 2. 2 Compute with all real and complex numbers. Checks for Understanding 3103. 2. 7 Graph complex numbers in the complex plane and recognize differences and similarities with the graphical representations of real numbers graphed on the number line. 3103. 2. 9 Find and describe geometrically the absolute value of a complex number.

Graphing Complex Numbers • Complex numbers cannot be graphed on a normal coordinate axes. • Complex numbers are graphed in an Argand diagram, which looks very much like a regular Cartesian coordinate axes. • An Argand diagram shows a relationship between the x-axis (real axis) with real numbers and the y-axis (imaginary axis) with imaginary numbers. • In an Argand diagram, a complex number (a + bi) is the point (a, b) or the vector from the origin to the point (a, b).

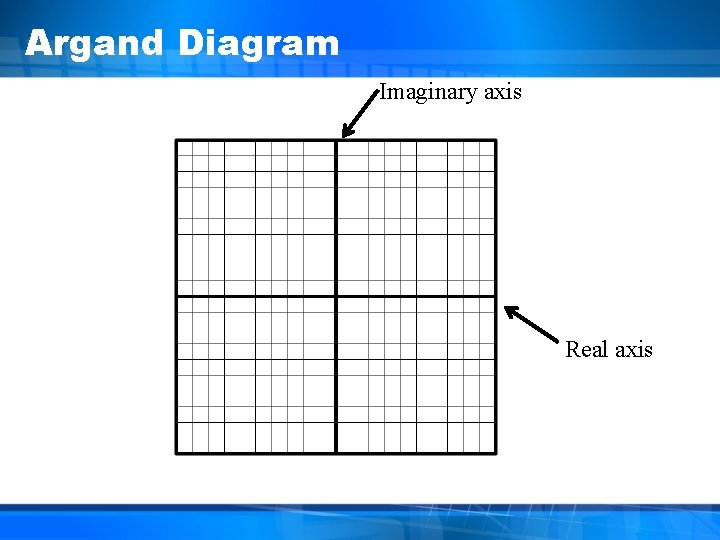
Argand Diagram Imaginary axis Real axis

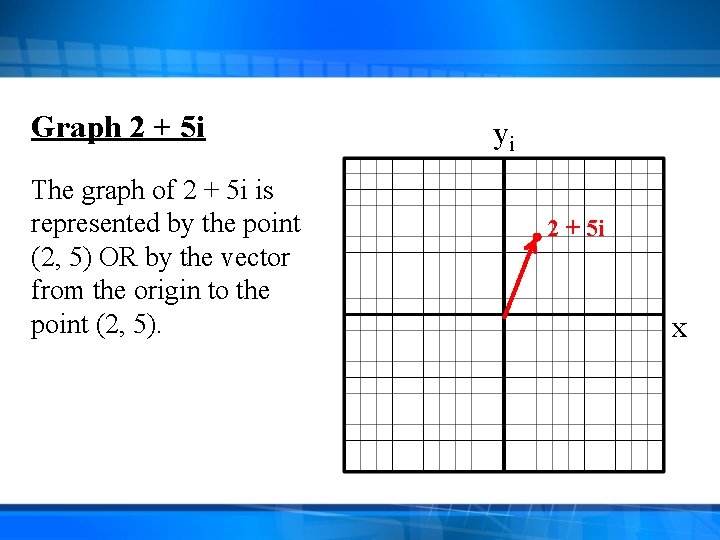
Graph 2 + 5 i The graph of 2 + 5 i is represented by the point (2, 5) OR by the vector from the origin to the point (2, 5). yi 2 + 5 i x

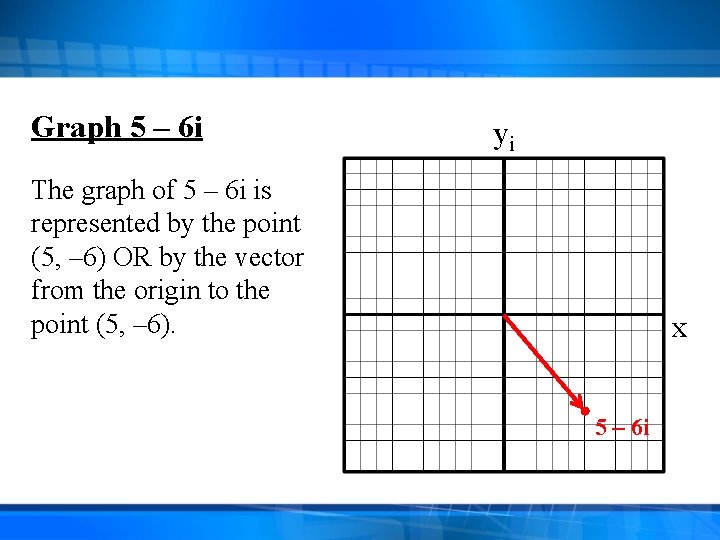
Graph 5 – 6 i yi The graph of 5 – 6 i is represented by the point (5, – 6) OR by the vector from the origin to the point (5, – 6). x 5 – 6 i

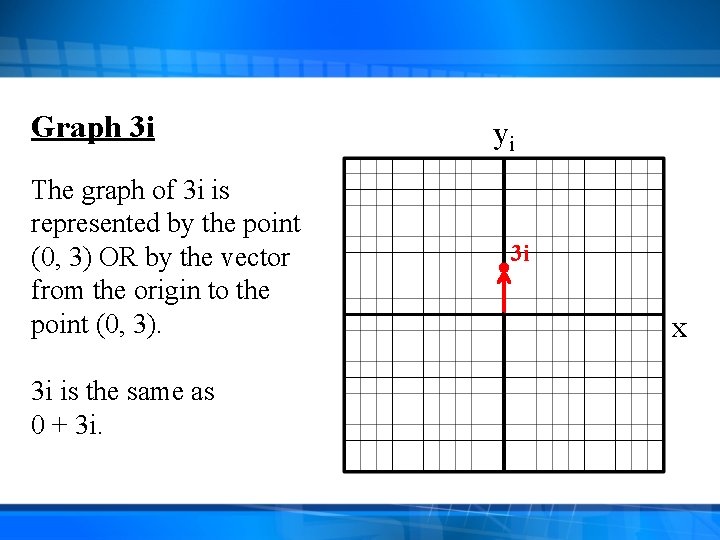
Graph 3 i The graph of 3 i is represented by the point (0, 3) OR by the vector from the origin to the point (0, 3). 3 i is the same as 0 + 3 i. yi 3 i x

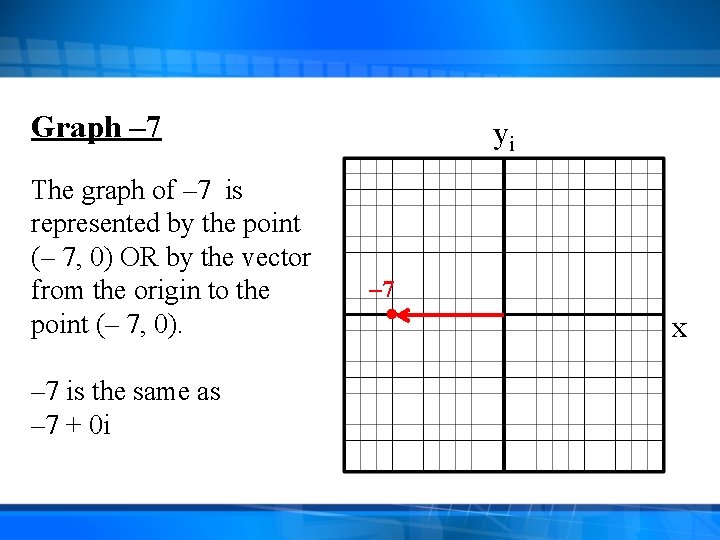
Graph – 7 The graph of – 7 is represented by the point (– 7, 0) OR by the vector from the origin to the point (– 7, 0). – 7 is the same as – 7 + 0 i yi – 7 x

Try These 1. – 2 + 7 i 2. – 6 – i 3. 2 4. 8 i

Absolute Value of Complex Numbers • The absolute value of a real number is the distance from zero to the number on the number line. • The absolute value of a complex number is also the distance from the number to zero, but the distance is measured from zero to the number in an Argand diagram rather than on a number line. • The most efficient method to find the absolute value of a complex number is derived from the Pythagorean Theorem.

Absolute Value of Complex Numbers • The absolute value of a complex number z = a + bi is written as z. • The absolute value of a complex number is a nonnegative real number defined as z =. • Since a complex number is represented by a point or by the vector from the origin to the point, the absolute value is the length of the vector, called the magnitude.

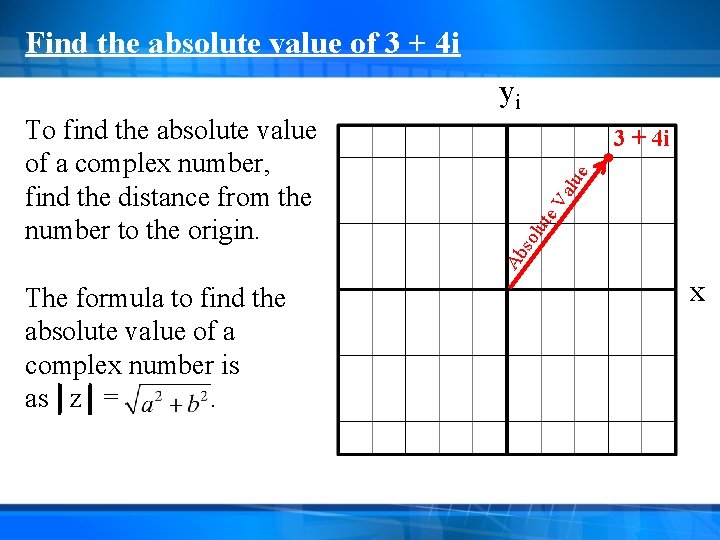
Find the absolute value of 3 + 4 i yi The formula to find the absolute value of a complex number is as z =. te Va lue 3 + 4 i Ab so lu To find the absolute value of a complex number, find the distance from the number to the origin. x

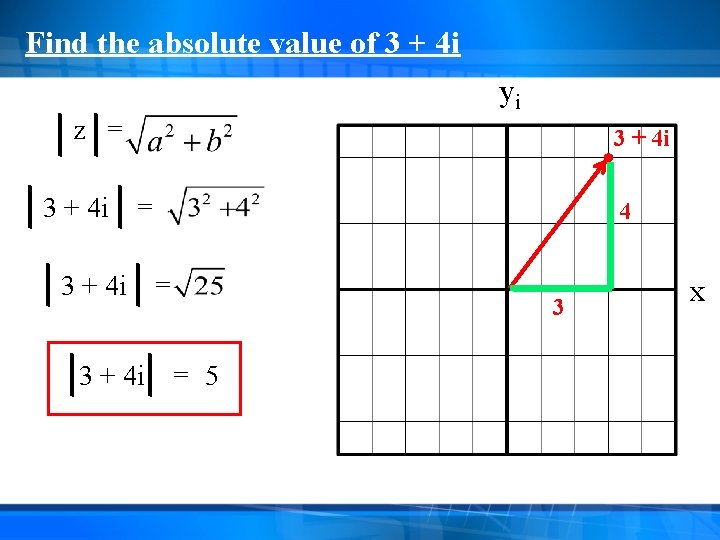
Find the absolute value of 3 + 4 i yi z = 3 + 4 i 4 = 3 = 5 x

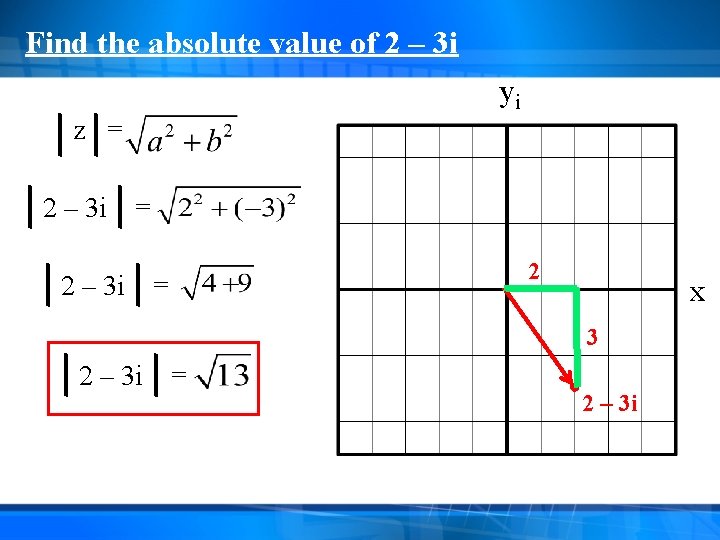
Find the absolute value of 2 – 3 i yi z = 2 – 3 i = = 2 x 3 2 – 3 i = 2 – 3 i

Try These 1. – 4 + 6 i 2. – 3 + 5 i