Graphing Absolute Value Translations of Parent Function 13

Graphing Absolute Value Translations of Parent Function /13 1

Absolute Value y = |x| › Remember, everything within the bars comes out as positive. › So unless something is being SUBTRACTED from it, or it’s being MULTIPLIED by a Negative, y will ONLY be positive! › Y = |x| is known as the Parent Function

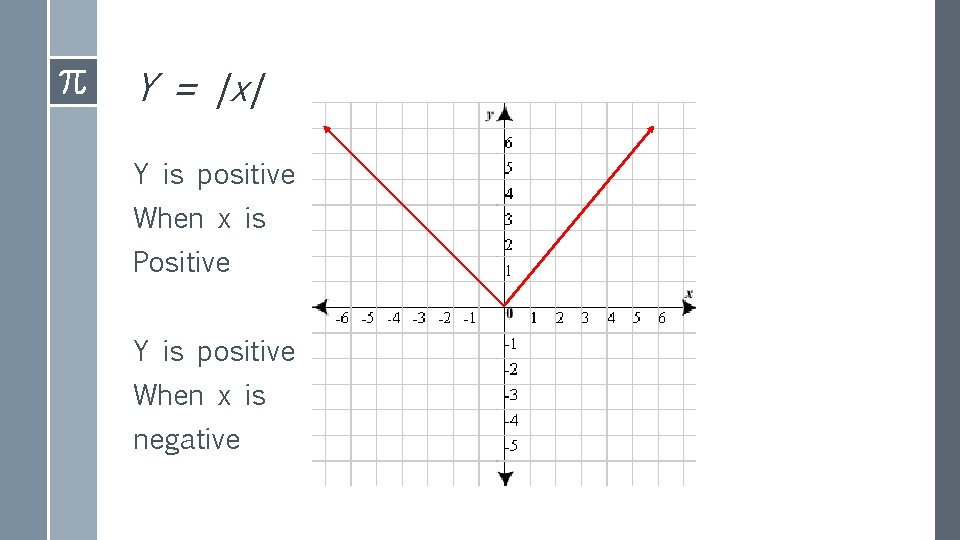
Y = |x| Y is positive When x is Positive Y is positive When x is negative

Absolute Value y = |x| › So you notice in the previous graph, there is a single point where the function changes direction – the tip of the V. › This point is known as the VERTEX of the function. › Many types of functions have vertices (plural or vertex). › An absolute value function is largely determined by the position of its vertex. In the Parent Function, it’s just the origin (0, 0) -- but it can be moved! › Moving the vertex is called “Translation”

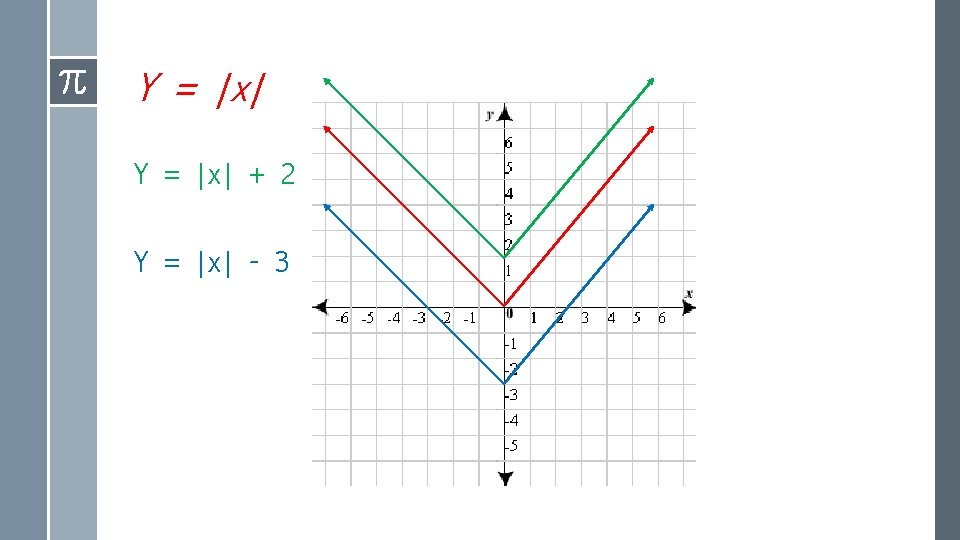
Translation › Shifting the Parent Function up or down, right or left is known as a TRANSLATION Vertical translation – moving the function up or down. y = |x| + k moves function UP k units y = |x| - k moves function DOWN k units

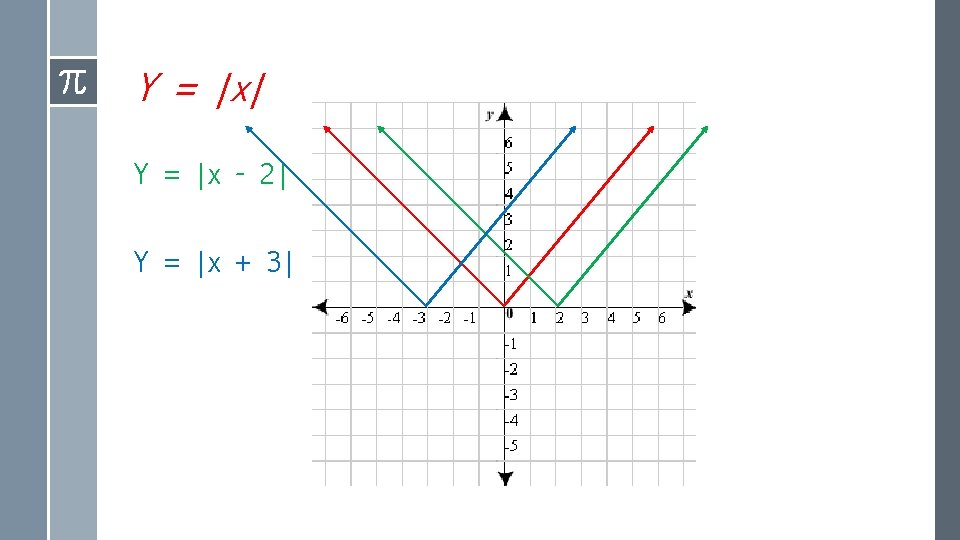
Translation › Horizontal Translations -- left or right shift of graph › WARNING! THIS ONE IS WEIRD!!!! › Left and right translations go the OPPOSITE way from what you would expect. › Y = | x – h| goes h units to the RIGHT!!!! › Y = |x + h| goes one units to the LEFT. › This is always so.

Translations › Of course, you can have both in the same equation. › There is a general form to show all possible transformations of the Absolute Value Function.

Work Together p. 221 Lesson Check 1 -13