Graphics 3 D Geometric Transformation Graphics Lab Korea

Graphics 3 D Geometric Transformation 고려대학교 그래픽스 연구실 Graphics Lab @ Korea University

Contents n Translation n Scaling n Rotation n Other Transformations n Coordinate Transformations CGVR Graphics Lab @ Korea University

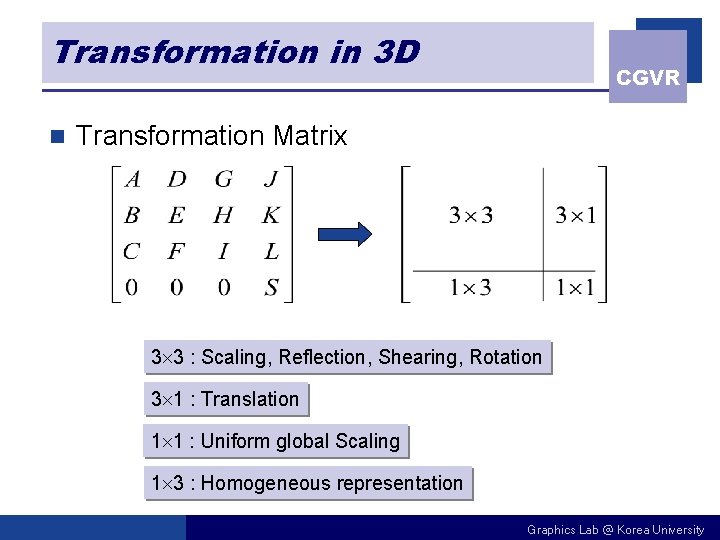
Transformation in 3 D n CGVR Transformation Matrix 3 3 : Scaling, Reflection, Shearing, Rotation 3 1 : Translation 1 1 : Uniform global Scaling 1 3 : Homogeneous representation Graphics Lab @ Korea University

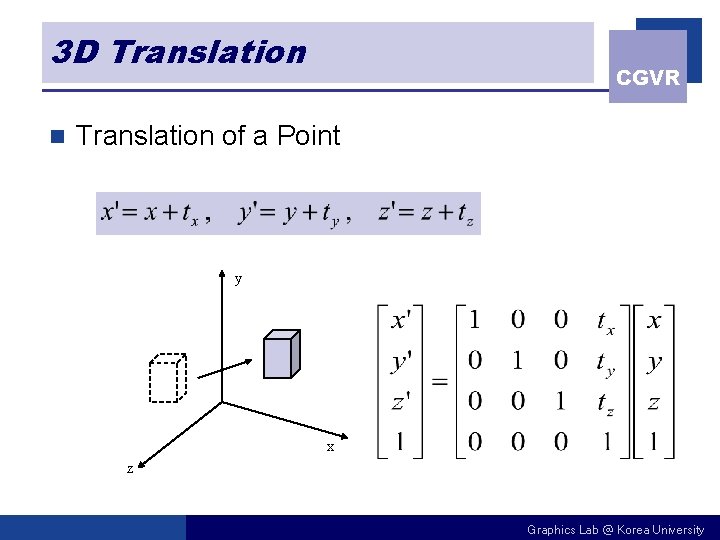
3 D Translation n CGVR Translation of a Point y x z Graphics Lab @ Korea University

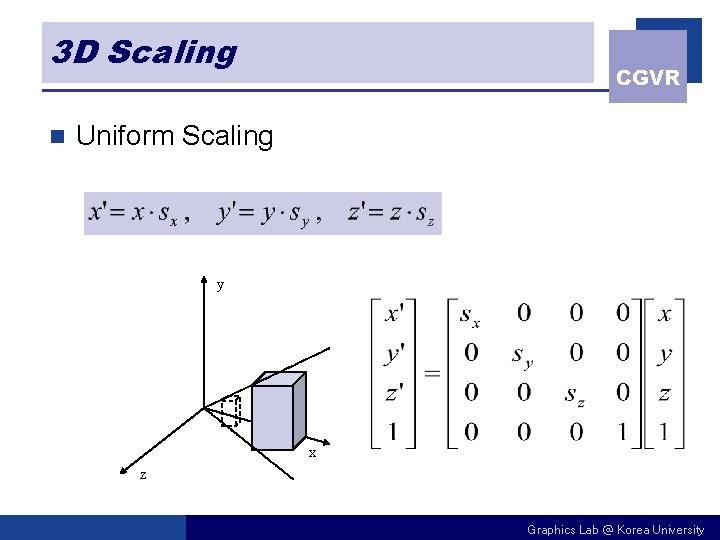
3 D Scaling n CGVR Uniform Scaling y x z Graphics Lab @ Korea University

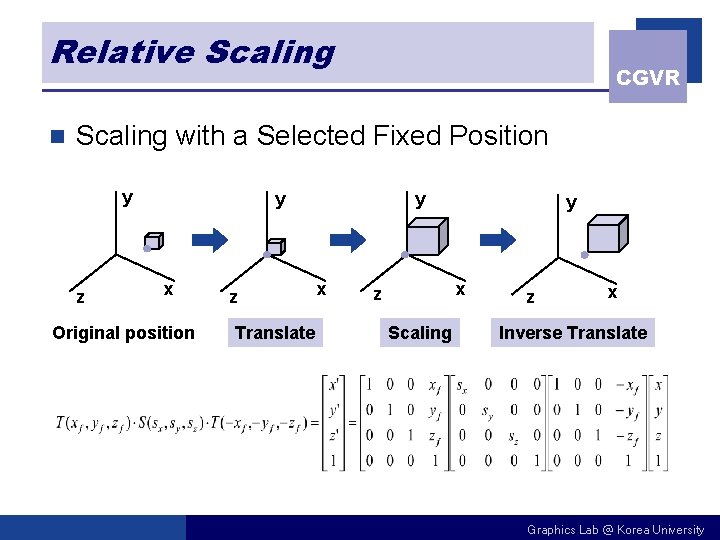
Relative Scaling n CGVR Scaling with a Selected Fixed Position y z y x Original position z Translate y x z Scaling z x Inverse Translate Graphics Lab @ Korea University

3 D Rotation n CGVR Coordinate-Axes Rotations X-axis rotation n Y-axis rotation n Z-axis rotation n n General 3 D Rotations Rotation about an axis that is parallel to one of the coordinate axes n Rotation about an arbitrary axis n Graphics Lab @ Korea University

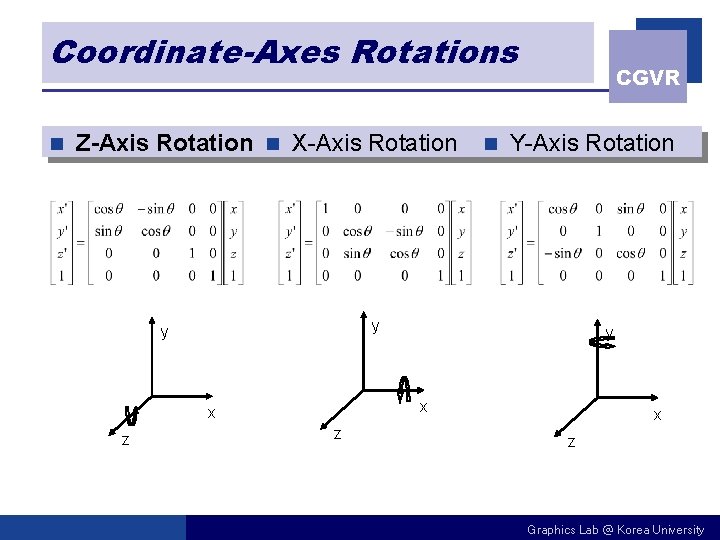
Coordinate-Axes Rotations n Z-Axis Rotation n X-Axis Rotation Y-Axis Rotation y y y x x z n CGVR z x z Graphics Lab @ Korea University

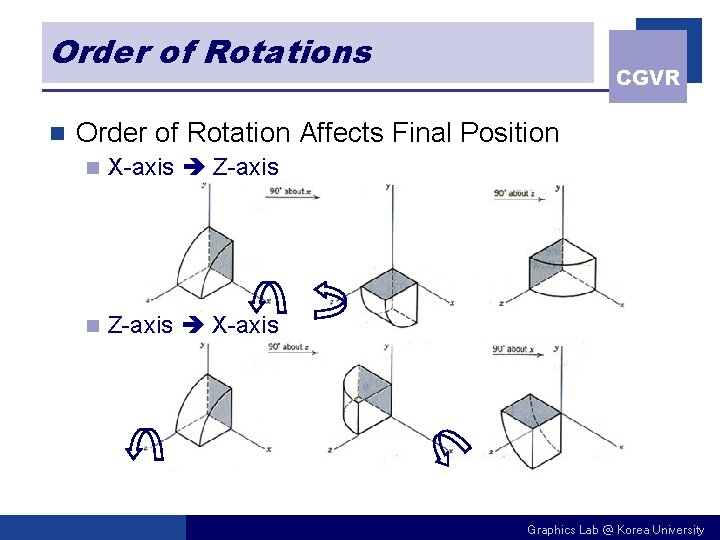
Order of Rotations n CGVR Order of Rotation Affects Final Position n X-axis Z-axis n Z-axis X-axis Graphics Lab @ Korea University

General 3 D Rotations n CGVR Rotation about an Axis that is Parallel to One of the Coordinate Axes Translate the object so that the rotation axis coincides with the parallel coordinate axis n Perform the specified rotation about that axis n Translate the object so that the rotation axis is moved back to its original position n Graphics Lab @ Korea University

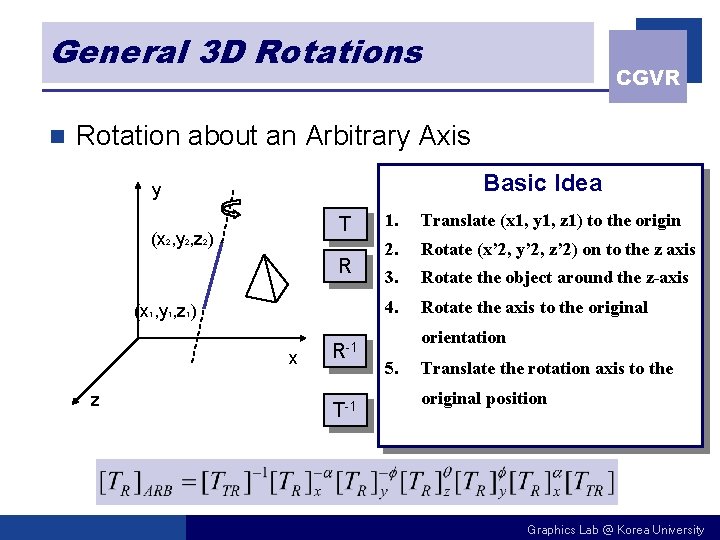
General 3 D Rotations n CGVR Rotation about an Arbitrary Axis Basic Idea y T (x 2, y 2, z 2) R (x 1, y 1, z 1) x z R-1 T-1 1. Translate (x 1, y 1, z 1) to the origin 2. Rotate (x’ 2, y’ 2, z’ 2) on to the z axis 3. Rotate the object around the z-axis 4. Rotate the axis to the original orientation 5. Translate the rotation axis to the original position Graphics Lab @ Korea University

General 3 D Rotations n CGVR Step 1. Translation y (x 2, y 2, z 2) (x 1, y 1, z 1) x z Graphics Lab @ Korea University

General 3 D Rotations n CGVR Step 2. Establish [ TR ] x x axis y (0, b, c) Projected Point (a, b, c) x z Rotated Point Graphics Lab @ Korea University

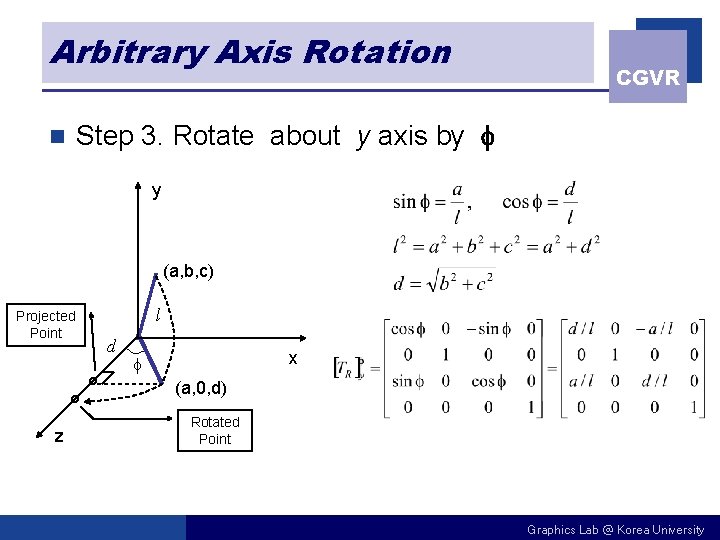
Arbitrary Axis Rotation n CGVR Step 3. Rotate about y axis by y (a, b, c) Projected Point l d x (a, 0, d) z Rotated Point Graphics Lab @ Korea University

Arbitrary Axis Rotation n CGVR Step 4. Rotate about z axis by the desired angle y l x z Graphics Lab @ Korea University

Arbitrary Axis Rotation n CGVR Step 5. Apply the reverse transformation to place the axis back in its initial position y l l x z Graphics Lab @ Korea University

Example CGVR Ex) Find the new coordinates of a unit cube 90ºrotated about an axis defined by its endpoints A(2, 1, 0) and B(3, 3, 1). A Unit Cube Graphics Lab @ Korea University

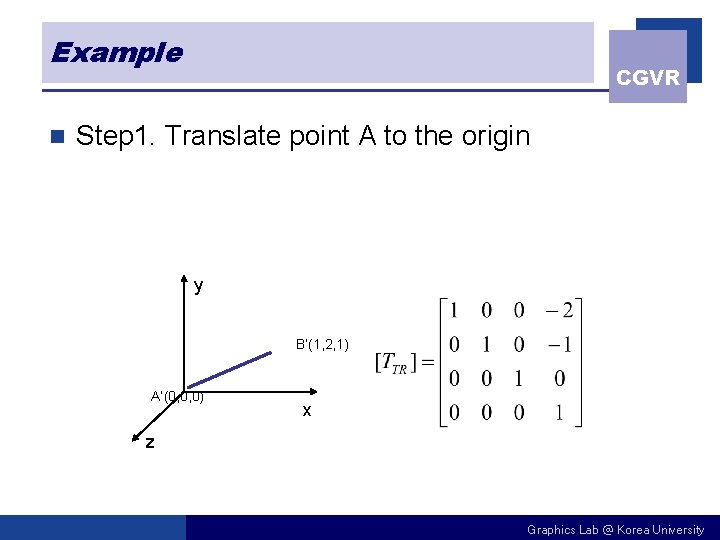
Example n CGVR Step 1. Translate point A to the origin y B’(1, 2, 1) A’(0, 0, 0) x z Graphics Lab @ Korea University

Example n CGVR Step 2. Rotate axis A’B’ about the x axis by and angle , until it lies on the xz plane. y Projected point (0, 2, 1) z B’(1, 2, 1) l x B”(1, 0, 5) Graphics Lab @ Korea University

Example n CGVR Step 3. Rotate axis A’B’’ about the y axis by and angle , until it coincides with the z axis. y (0, 0, 6) l x B”(1, 0, 5) z Graphics Lab @ Korea University

Example n CGVR Step 4. Rotate the cube 90° about the z axis Finally, the concatenated rotation matrix about the arbitrary axis AB becomes, Graphics Lab @ Korea University

Example CGVR Graphics Lab @ Korea University

Example n CGVR Multiplying [TR]AB by the point matrix of the original cube Graphics Lab @ Korea University

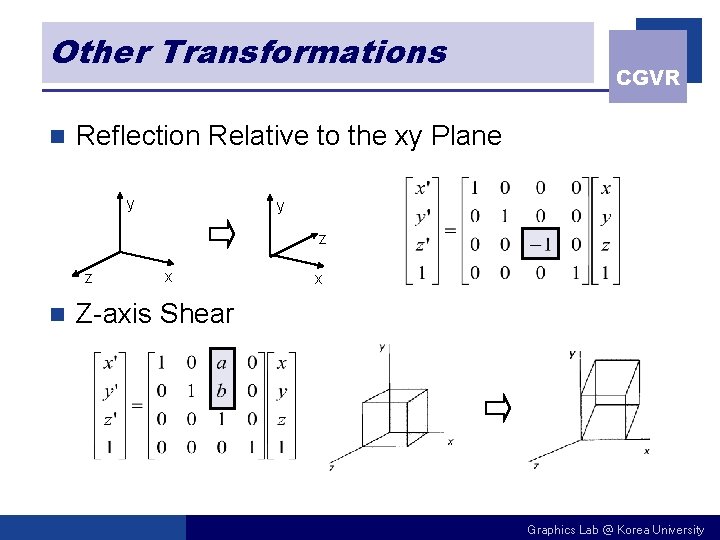
Other Transformations n CGVR Reflection Relative to the xy Plane y y z z n x x Z-axis Shear Graphics Lab @ Korea University

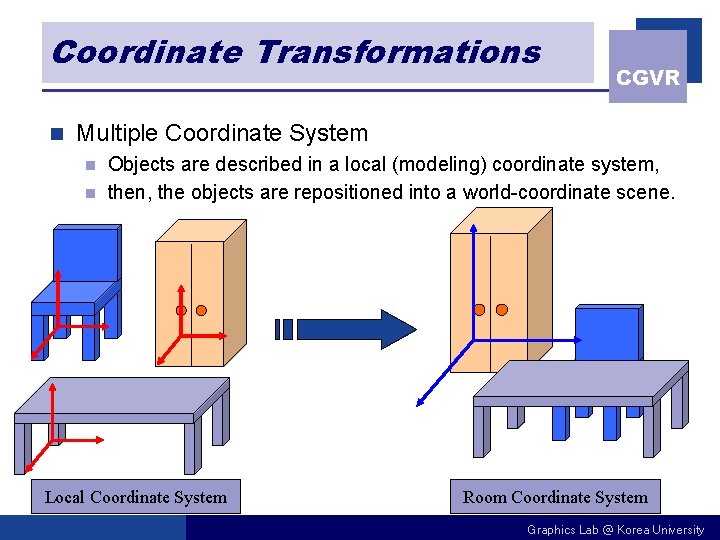
Coordinate Transformations n CGVR Multiple Coordinate System Objects are described in a local (modeling) coordinate system, n then, the objects are repositioned into a world-coordinate scene. n Local Coordinate System Room Coordinate System Graphics Lab @ Korea University

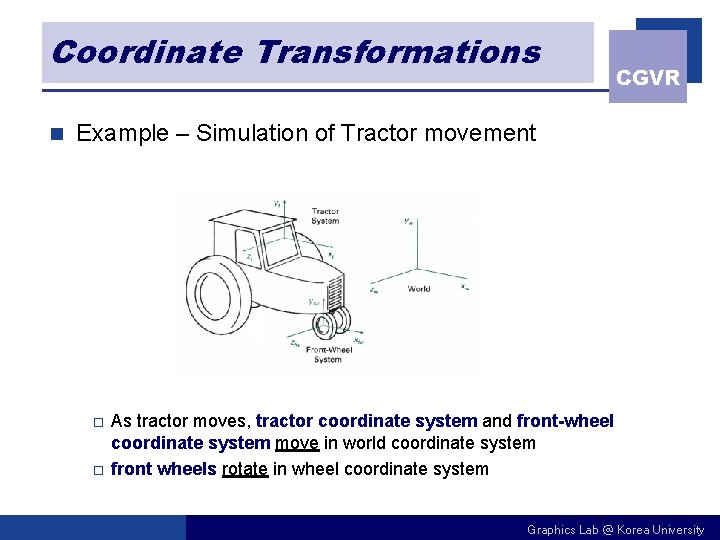
Coordinate Transformations n CGVR Example – Simulation of Tractor movement o o As tractor moves, tractor coordinate system and front-wheel coordinate system move in world coordinate system front wheels rotate in wheel coordinate system Graphics Lab @ Korea University

Coordinate Transformations CGVR Transformation of an Object Description from One Coordinate System to Another n Transformation Matrix n n brings the two coordinates systems into alignment 1. Translation (0, 0, 0) (x 0, y 0, z 0) x z’ y x’ u’y y z y’ u’y u’x u’z z u’x (0, 0, 0) x u’z T(-x 0, -y 0, -z 0) Graphics Lab @ Korea University

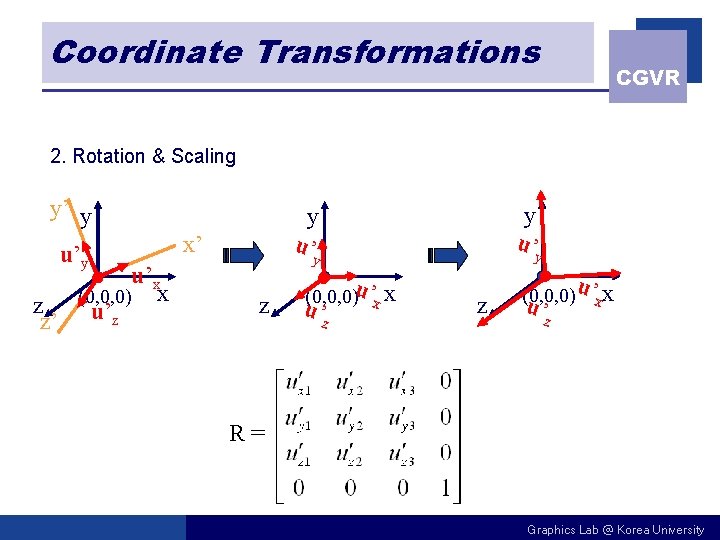
Coordinate Transformations CGVR 2. Rotation & Scaling y’ y u’x x z (0, 0, 0) z’ u’z y u’ y x’ z (0, 0, 0)u’x x u’ z z (0, 0, 0)u’xx u’ z R= Graphics Lab @ Korea University