Graphical Representation of Internal Forces in Beams Shear

Graphical Representation of Internal Forces in Beams: Shear and Moment Diagrams ES 2501: Statics/Unit 21 -1: Introduction: Shear and moment diagrams give a graphical representation of the internal forces in a beam as how the shear and bending moment distributed over the span of a bear. The maximum shear and bending moment can be easily identified for structural design. As the first step a general expression for the internal forces of a beam need to be found for ANY arbitrary position as a function of position. An arbitrary position designated by variable, x N(x) is zero in the case of loading is perpendicular to the axis of a straight beam Internal forces at ANY arbitrary position ss functions of a variable of x

ES 2501: Statics/Unit 21 -2: Internal Forces in Beams Example 1: Draw the shear and moment diagram for a simply-supported subjected to a point load. Support Reactions: General Expressions for Internal forces: Case I: for a typical cross-section I between points A and C, i. e. Note: this set of expressions apply for any position between A and C, i, e, ONLY

ES 2501: Statics/Unit 21 -3: Example 1 (con’d): Internal Forces in Beams General Expressions for Internal forces: Case 2: for a typical cross-section II between points C and B, i. e. Two typical cross-sections are needed due to existence of the point load, P, which make the internal forces discontinuous and mathematically speaking, piecewise expressions for the Internal forces are necessary. Note: this set of expressions apply for any position between C and B, i, e, ONLY

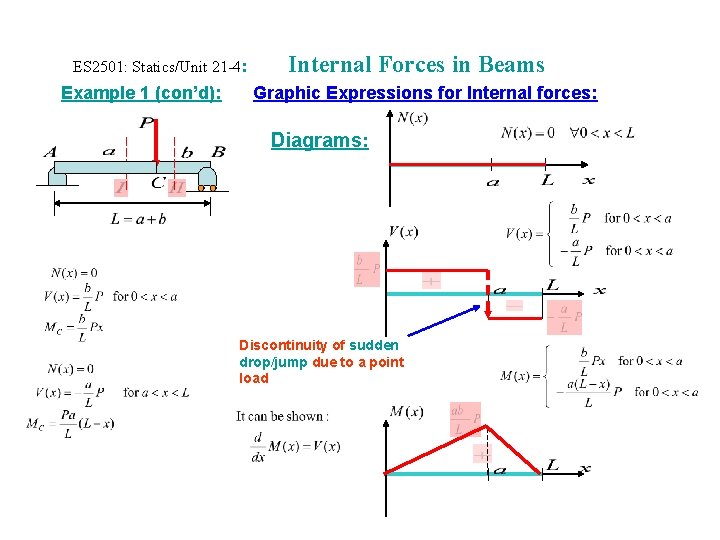
ES 2501: Statics/Unit 21 -4: Example 1 (con’d): Internal Forces in Beams Graphic Expressions for Internal forces: Diagrams: Discontinuity of sudden drop/jump due to a point load

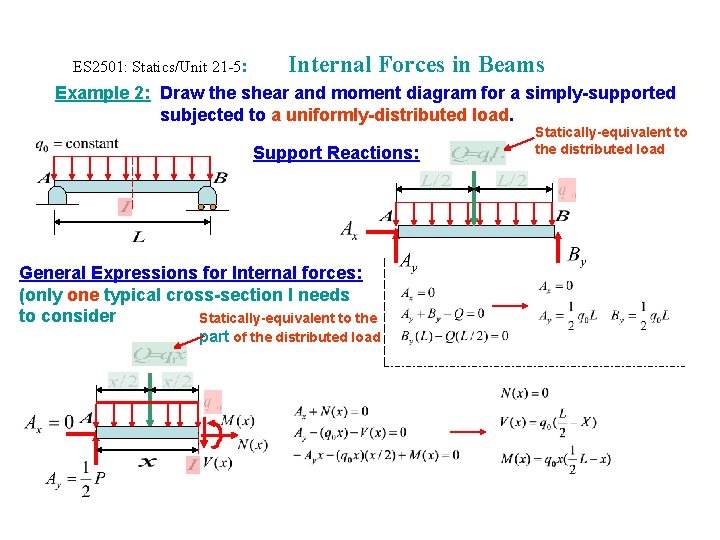
ES 2501: Statics/Unit 21 -5: Internal Forces in Beams Example 2: Draw the shear and moment diagram for a simply-supported subjected to a uniformly-distributed load. Support Reactions: General Expressions for Internal forces: (only one typical cross-section I needs to consider Statically-equivalent to the part of the distributed load Statically-equivalent to the distributed load

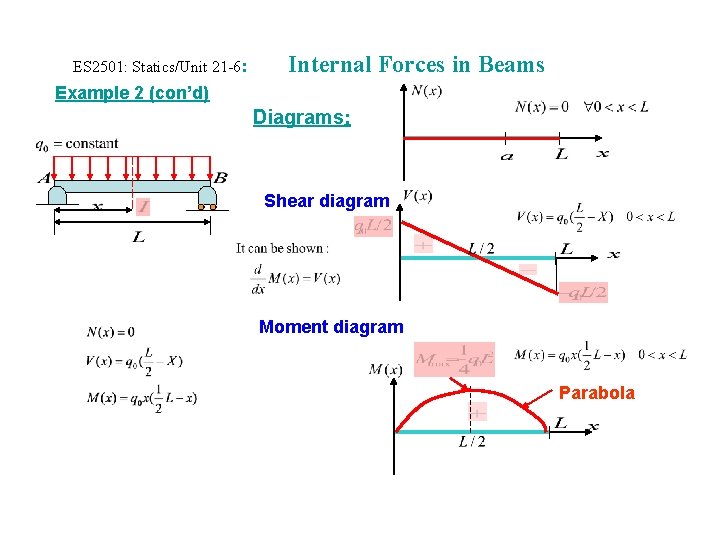
ES 2501: Statics/Unit 21 -6: Internal Forces in Beams Example 2 (con’d) Diagrams: Shear diagram Moment diagram Parabola

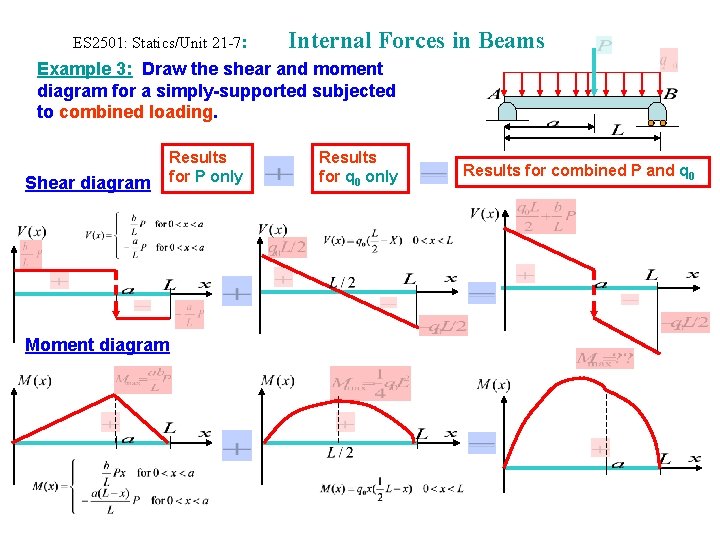
ES 2501: Statics/Unit 21 -7: Internal Forces in Beams Example 3: Draw the shear and moment diagram for a simply-supported subjected to combined loading. Shear diagram Moment diagram Results for P only Results for q 0 only Results for combined P and q 0