Graphical Models for Game Theory Undirected graph G










: T[r+1](w,](https://slidetodoc.com/presentation_image/0bf2ec9670e86f4a65c92742fc380aef/image-16.jpg)







- Slides: 23










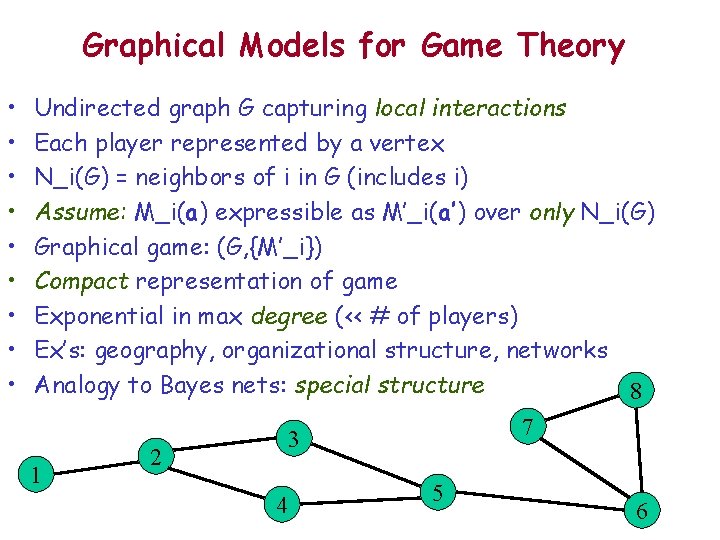
Graphical Models for Game Theory • • • Undirected graph G capturing local interactions Each player represented by a vertex N_i(G) = neighbors of i in G (includes i) Assume: M_i(a) expressible as M’_i(a’) over only N_i(G) Graphical game: (G, {M’_i}) Compact representation of game Exponential in max degree (<< # of players) Ex’s: geography, organizational structure, networks Analogy to Bayes nets: special structure 8 1 7 3 2 4 5 6

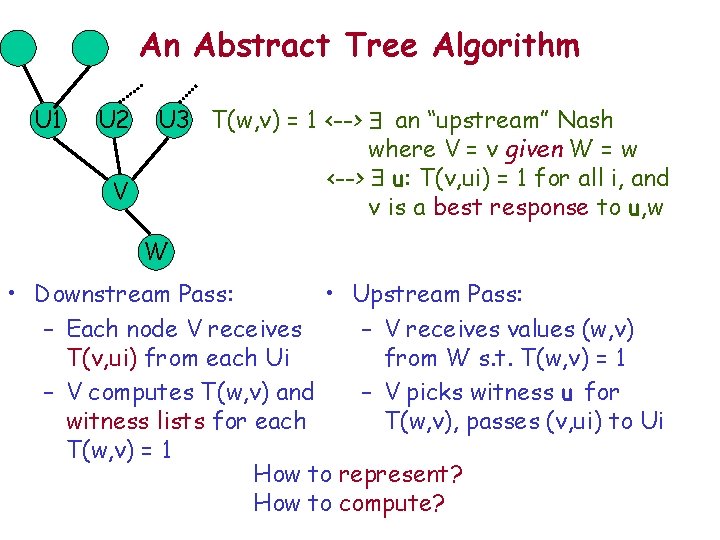
An Abstract Tree Algorithm U 1 U 2 V U 3 T(w, v) = 1 <--> $ an “upstream” Nash where V = v given W = w <--> $ u: T(v, ui) = 1 for all i, and v is a best response to u, w W • Downstream Pass: • Upstream Pass: – Each node V receives – V receives values (w, v) T(v, ui) from each Ui from W s. t. T(w, v) = 1 – V computes T(w, v) and – V picks witness u for witness lists for each T(w, v), passes (v, ui) to Ui T(w, v) = 1 How to represent? How to compute?

An Approximation Algorithm • Discretize u and v in T(v, u), 1 represents approximate Nash • Main technical lemma: If k is max degree, grid resolution t ~ e/k preserves global e. Nash equilibria • An efficient algorithm: – Polynomial in n (fixed k) U 1 – Represent an approx. to every Nash – Can generate random Nash, or specific Nash U 2 U 3 V W

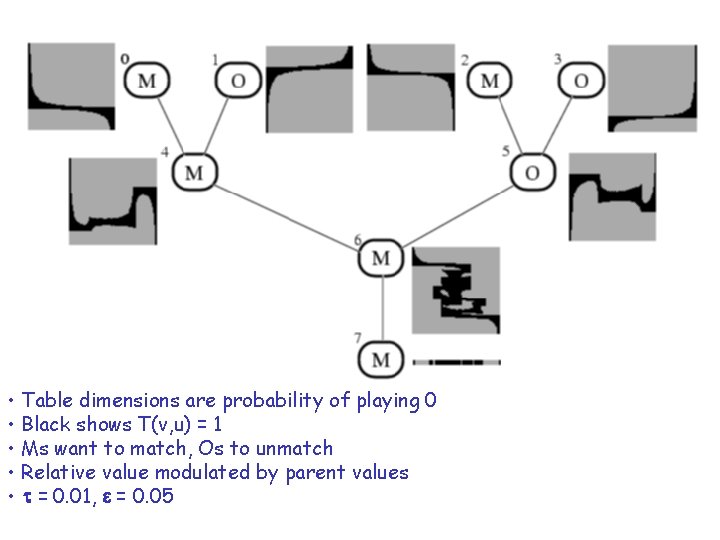
• Table dimensions are probability of playing 0 • Black shows T(v, u) = 1 • Ms want to match, Os to unmatch • Relative value modulated by parent values • t = 0. 01, e = 0. 05

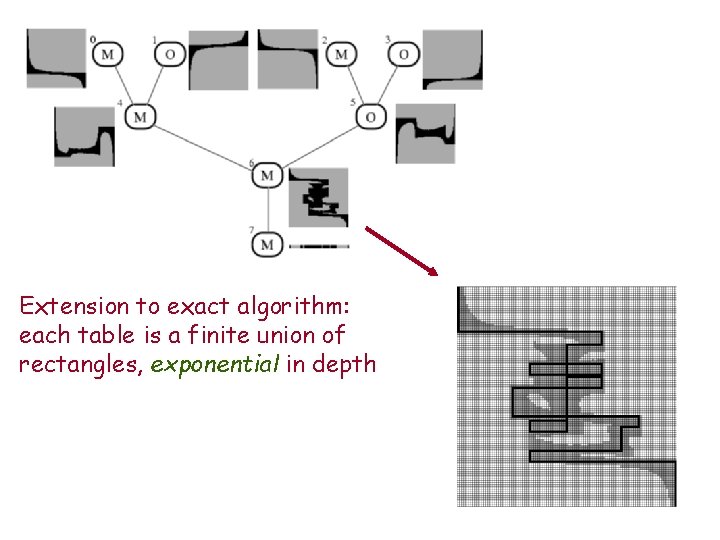
Extension to exact algorithm: each table is a finite union of rectangles, exponential in depth

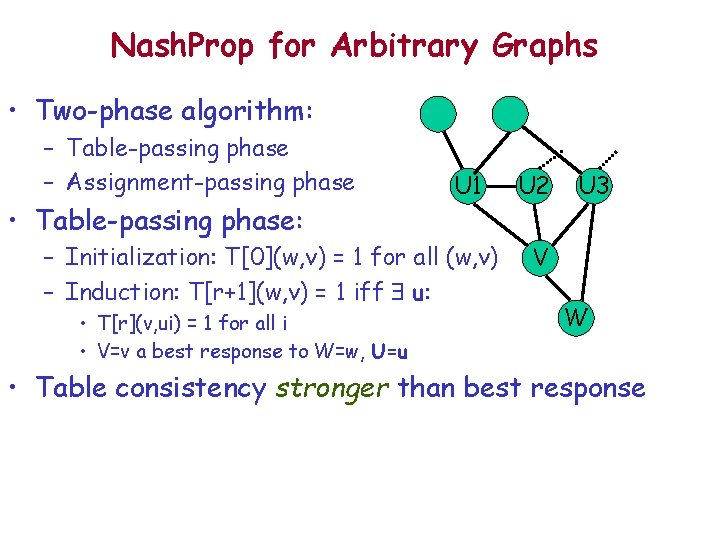
Nash. Prop for Arbitrary Graphs • Two-phase algorithm: – Table-passing phase – Assignment-passing phase • Table-passing phase: U 1 – Initialization: T[0](w, v) = 1 for all (w, v) – Induction: T[r+1](w, v) = 1 iff $ u: • T[r](v, ui) = 1 for all i • V=v a best response to W=w, U=u U 2 U 3 V W • Table consistency stronger than best response

Convergence of Table-Passing • Table-passing obeys contraction: • • • – {(w, v): T[r+1](w, v) = 1} contained in {(w, v): T[r](w, v) = 1} Tables converge and are balanced Discretization scheme: tables converge quickly Never eliminate an equilibrium Tables give a reduced search space Assignment-passing phase: – Use graph to propagate a solution consistent with tables – Backtracking local search • Allow e and t to be parameters • Alternative approach [Vickrey&Koller]: – Constraint propagation on junction tree







Graphical Games: Related Work • • Koller and Milch: graphical influence diagrams La Mura: game networks Vickrey & Koller: other methods on graphical games Leyton-Brown: action-graph games