Graphical Look at Motion displacement time curve l

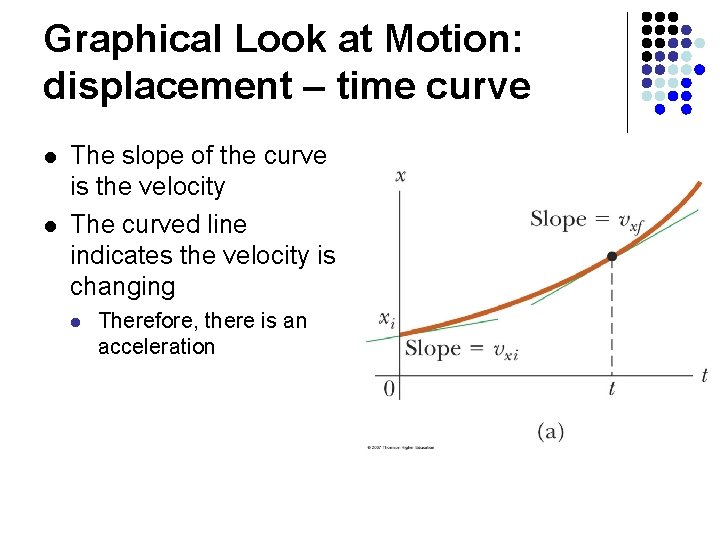
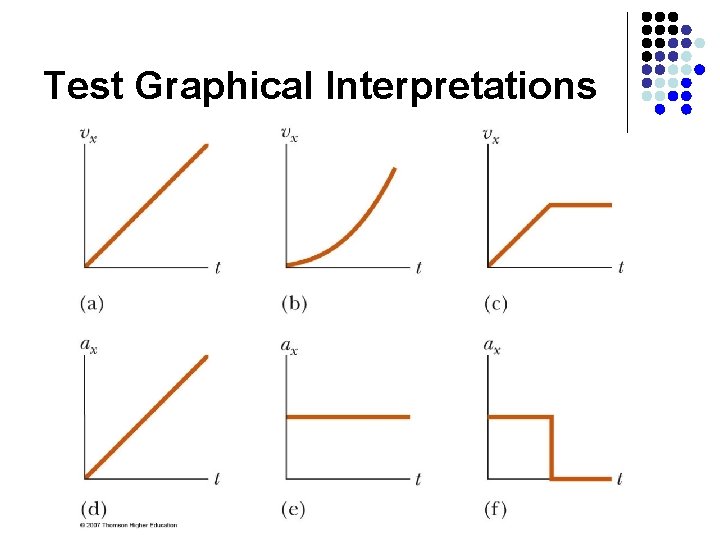
Graphical Look at Motion: displacement – time curve l l The slope of the curve is the velocity The curved line indicates the velocity is changing l Therefore, there is an acceleration

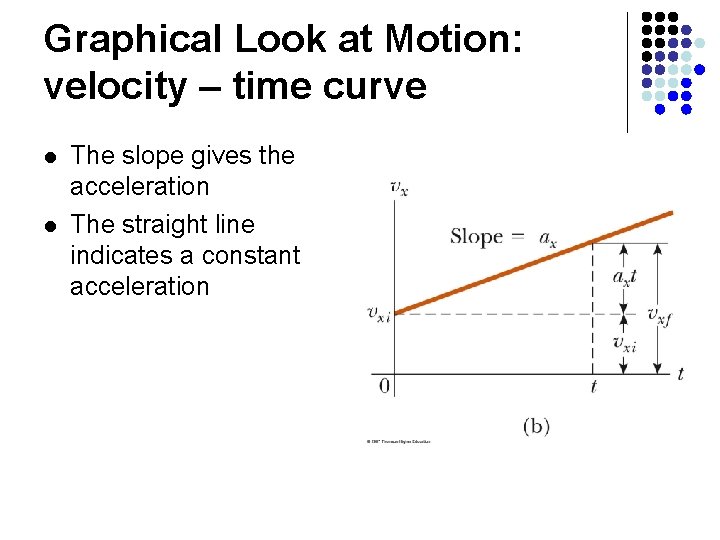
Graphical Look at Motion: velocity – time curve l l The slope gives the acceleration The straight line indicates a constant acceleration

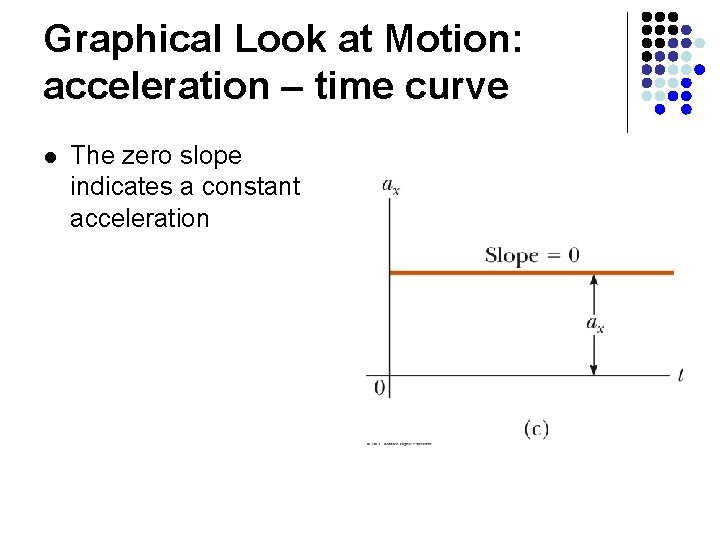
Graphical Look at Motion: acceleration – time curve l The zero slope indicates a constant acceleration

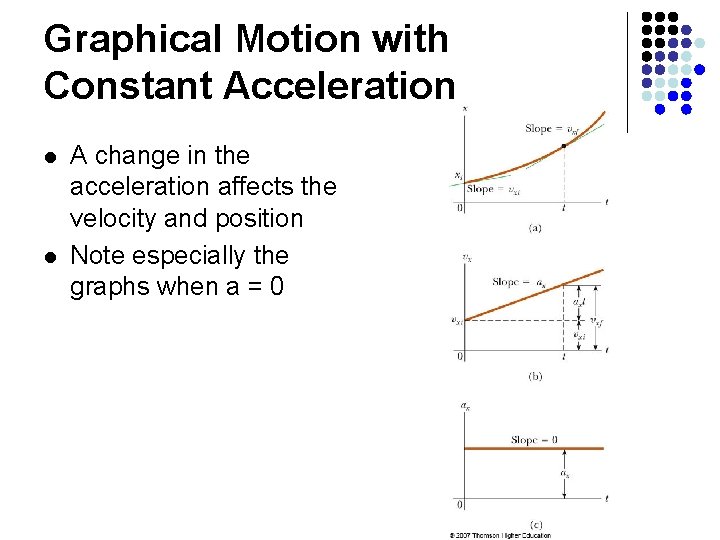
Graphical Motion with Constant Acceleration l l A change in the acceleration affects the velocity and position Note especially the graphs when a = 0

Test Graphical Interpretations

Kinematic Equations – summary

Kinematic Equations l l The kinematic equations can be used with any particle under uniform acceleration. The kinematic equations may be used to solve any problem involving one-dimensional motion with a constant acceleration You may need to use two of the equations to solve one problem Many times there is more than one way to solve a problem

Kinematic Equations, specific l l For constant a, vf = vi + at Can determine an object’s velocity at any time t when we know its initial velocity and its acceleration l l Assumes ti = 0 and tf = t Does not give any information about displacement

Kinematic Equations, specific l For constant acceleration, vavg = vi + vf 2 l The average velocity can be expressed as the arithmetic mean of the initial and final velocities

Kinematic Equations, specific l For constant acceleration, l This gives you the position of the particle in terms of time and velocities Doesn’t give you the acceleration l

Kinematic Equations, specific l For constant acceleration, l Gives final position in terms of velocity and acceleration Doesn’t tell you about final velocity l

Kinematic Equations, specific l For constant a, l Gives final velocity in terms of acceleration and displacement Does not give any information about the time l

When a = 0 l When the acceleration is zero, l l l vf = vi = v xf = xi + v t The constant acceleration model reduces to the constant velocity model

Freely Falling Objects l l A freely falling object is any object moving freely under the influence of gravity alone. It does not depend upon the initial motion of the object l l l Dropped – released from rest Thrown downward Thrown upward

Acceleration of Freely Falling Object l l The acceleration of an object in free fall is directed downward, regardless of the initial motion The magnitude of free fall acceleration is g = - 9. 80 m/s 2 l l l g decreases with increasing altitude 9. 80 m/s 2 is the average at the Earth’s surface The italicized g will be used for the acceleration due to gravity l Not to be confused with g for grams

Acceleration of Free Fall, cont. l l We will neglect air resistance Free fall motion is constantly accelerated motion in one dimension Let upward be positive Use the kinematic equations with ay = -g = -9. 80 m/s 2

Free Fall – an object dropped l l l Initial velocity is zero Let up be positive Use the kinematic equations l l Generally use y instead of x since vertical Acceleration is l ay = -g = -9. 80 m/s 2 vo= 0 a = -g

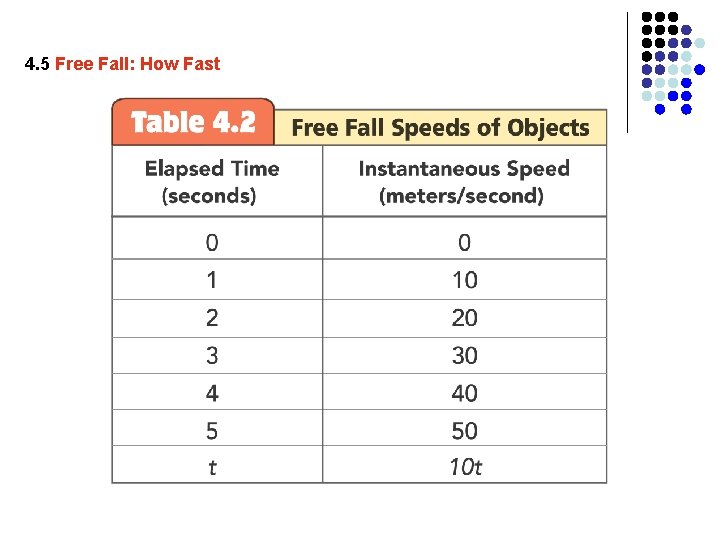
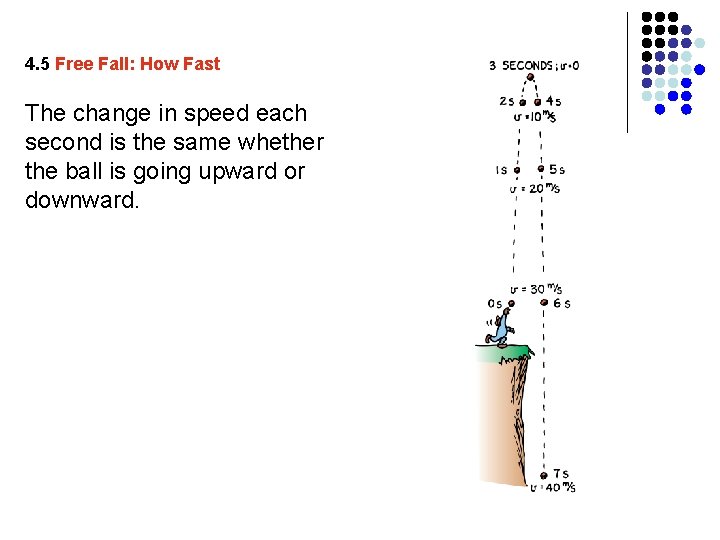
4. 5 Free Fall: How Fast The instantaneous speed of an object falling from rest is equal to the acceleration multiplied by the elapsed time. v = - gt The letter v represents both speed and velocity. When the acceleration g = 9. 8 m/s 2 is multiplied by the elapsed time in seconds, the result is the instantaneous speed in meters per second.

4. 5 Free Fall: How Fast If a falling rock were somehow equipped with a speedometer, in each succeeding second of fall its reading would increase by the same amount, 9. 8 m/s.

4. 5 Free Fall: How Fast

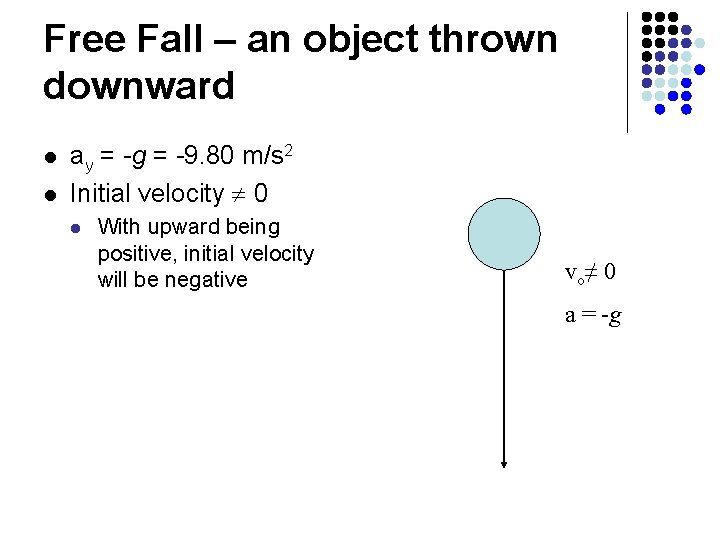
Free Fall – an object thrown downward l l ay = -g = -9. 80 m/s 2 Initial velocity 0 l With upward being positive, initial velocity will be negative vo≠ 0 a = -g

4. 5 Free Fall: How Fast Rising Objects Now consider an object thrown straight up: It moves upward for a while. At the highest point, when the object is changing its direction from upward to downward, its instantaneous speed is zero. It then falls downward as if it had been dropped from rest at that height.

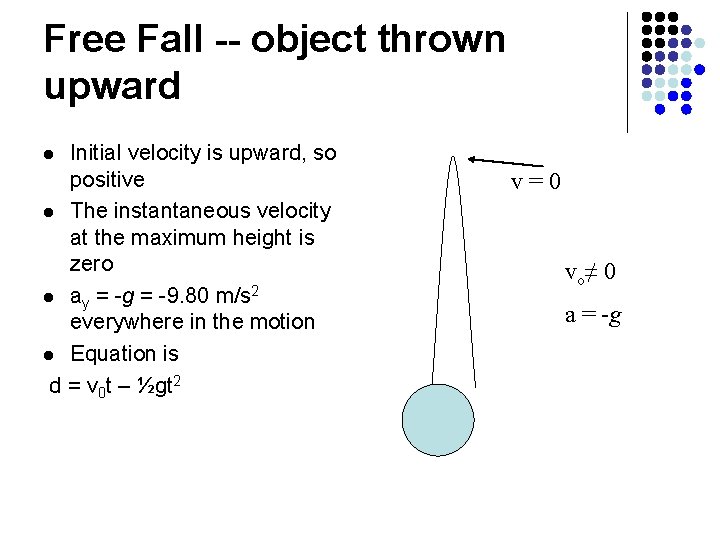
Free Fall -- object thrown upward Initial velocity is upward, so positive l The instantaneous velocity at the maximum height is zero l ay = -g = -9. 80 m/s 2 everywhere in the motion l Equation is d = v 0 t – ½gt 2 l v=0 vo≠ 0 a = -g

Thrown upward, cont. l The motion may be symmetrical l Then tup = tdown Then v = -vo The motion may not be symmetrical l Break the motion into various parts

Free Fall Example l l Initial velocity at A is upward (+) and acceleration is -g (-9. 8 m/s 2) At B, the velocity is 0 and the acceleration is -g (-9. 8 m/s 2) At C, the velocity has the same magnitude as at A, but is in the opposite direction The displacement is – 50. 0 m (it ends up 50. 0 m below its starting point)

4. 5 Free Fall: How Fast The change in speed each second is the same whether the ball is going upward or downward.

1. A rock is dropped from the top of an overhang and strikes the ground 6. 5 seconds later. How high is the overhang in meters? 2. What is the acceleration due to gravity on a planet if it takes 3. 45 s for an object to drop from a distance of 65 m? 3. A ball is thrown vertically upward with a speed of 25. 0 m/s a. How high does the ball fly? b. How long does it take to reach its highest point? c. How long does it take to reach the ground after its highest point? d. What is the speed of the ball as it reaches the level at which it was thrown?

1. A rock is dropped from the top of an overhang and strikes the ground 6. 5 seconds later. How high is the overhang in meters?

2. What is the acceleration due to gravity on a planet if it takes 3. 45 s for an object to drop from a distance of 65 m?

3. A ball is thrown vertically upward with a speed of 25. 0 m/s a. How high does the ball fly? b. How long does it take to reach its highest point? c. How long does it take to reach the ground after its highest point? d. What is the speed of the ball as it reaches the level at which it was thrown?