Graphic Organizers 1 Graphic Organizers GOs A graphic

Graphic Organizers 1

Graphic Organizers (GOs) A graphic organizer is a tool or process to build word knowledge by relating similarities of meaning to the definition of a word. This can relate to any subject—math, history, literature, etc. 2

Why are Graphic Organizers Important? • GOs connect content in a meaningful way to help you gain a clearer understanding of the material • GOs help maintain the information over time 3

Graphic Organizers: • Assist in organizing and retaining information when used consistently. 4

Coherent Graphic Organizers 1. Provide clearly labeled branch and sub branches. 2. Have numbers, arrows, or lines to show the connections or sequence of events. 3. Relate similarities. 4. Define accurately. 5

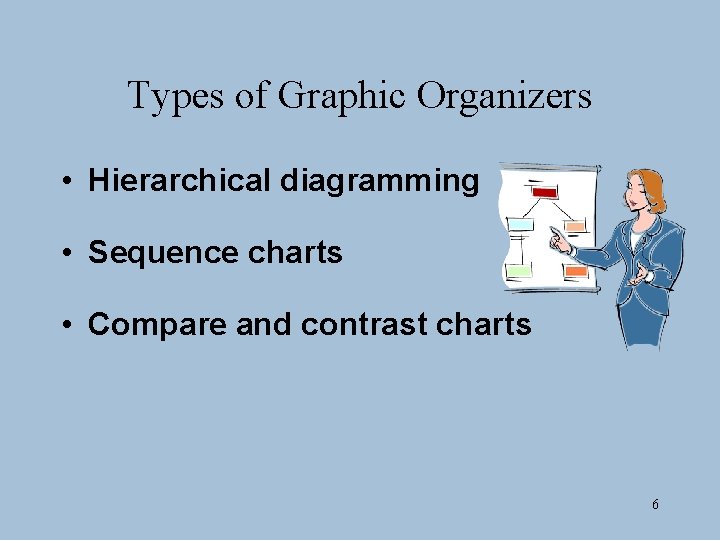
Types of Graphic Organizers • Hierarchical diagramming • Sequence charts • Compare and contrast charts 6

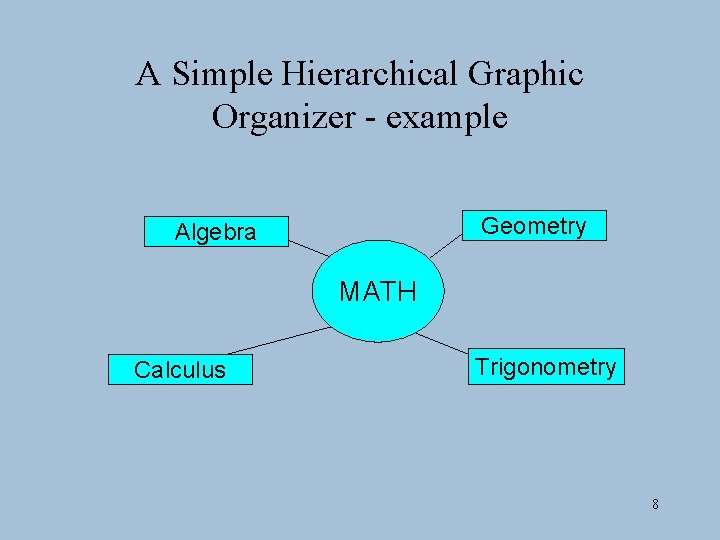
A Simple Hierarchical Graphic Organizer 7

A Simple Hierarchical Graphic Organizer - example Geometry Algebra MATH Calculus Trigonometry 8

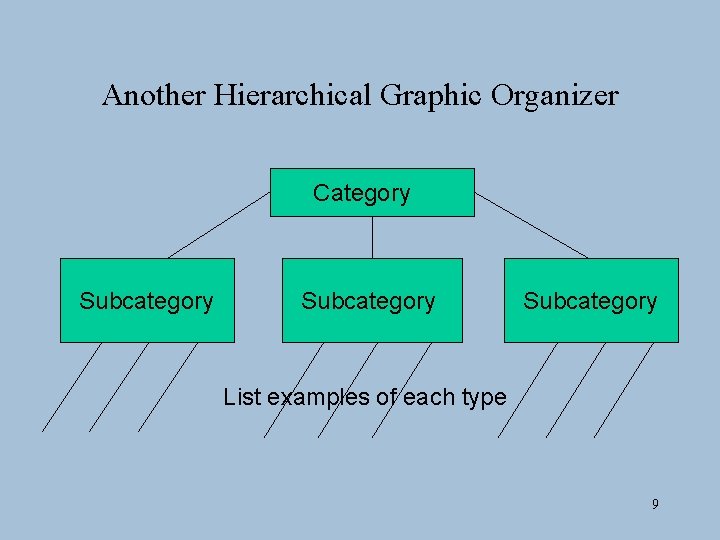
Another Hierarchical Graphic Organizer Category Subcategory List examples of each type 9

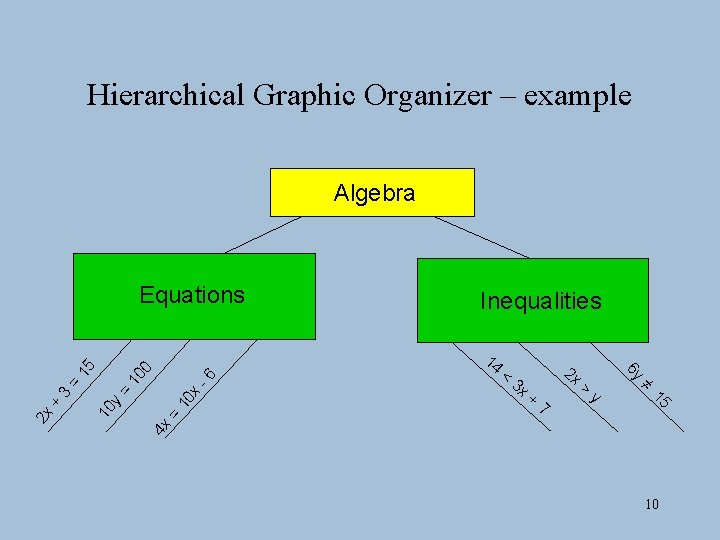
Hierarchical Graphic Organizer – example Algebra 3 x 2 x + 7 > y 4 x = 10 x -6 10 0 = 10 y = 3 < 15 + 14 ≠ 2 x Inequalities 6 y 15 Equations 10

Compare and Contrast Category Illustration/Example What is it? Properties/Attributes Subcategory Irregular set What are some examples? What is it like? 11

Compare and Contrast - example Numbers Illustration/Example What is it? 6, 17, 25, 100 -3, -8, -4000 Properties/Attributes Positive Integers Whole Numbers 0 Negative Integers Zero Fractions What are some examples? What is it like? 12

Venn Diagram 13

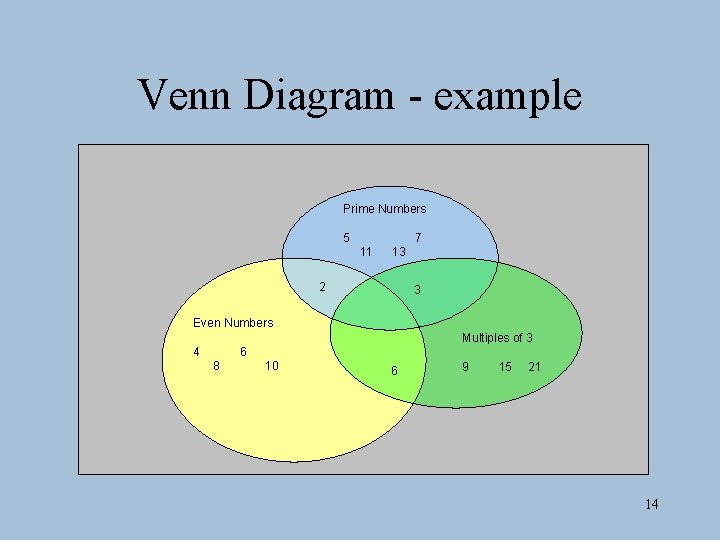
Venn Diagram - example Prime Numbers 5 7 11 13 2 3 Even Numbers Multiples of 3 4 6 8 10 6 9 15 21 14

Multiple Meanings 15

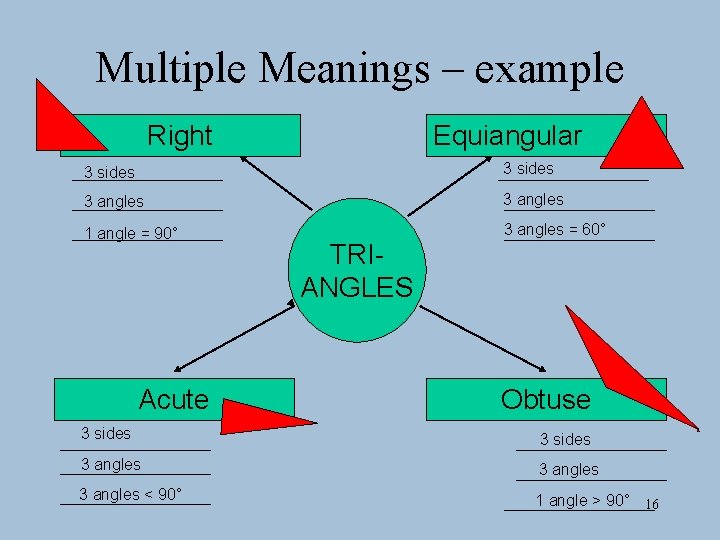
Multiple Meanings – example Right Equiangular 3 sides 3 angles 1 angle = 90° 3 angles = 60° Acute TRIANGLES Obtuse 3 sides 3 angles < 90° 1 angle > 90° 16

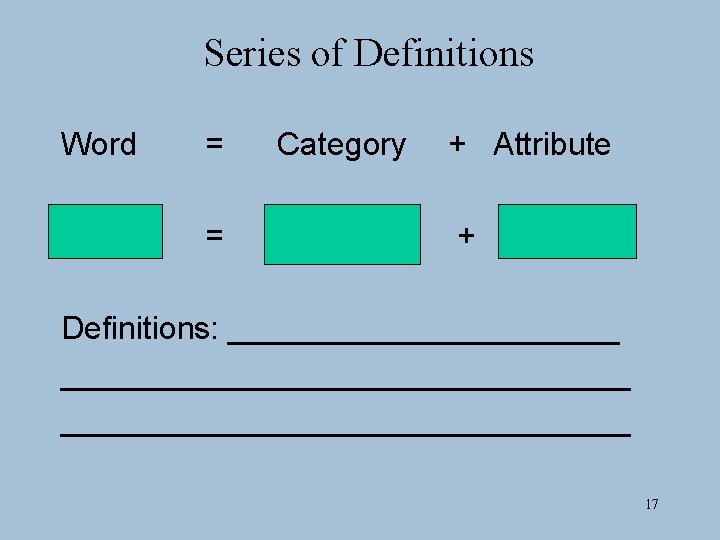
Series of Definitions Word = = Category + Attribute + Definitions: ___________________________ 17

Series of Definitions – example Word = Category Square = Quadrilateral + Attribute + 4 equal sides & 4 equal angles (90°) Definition: A four-sided figure with four equal sides and four right angles. 18

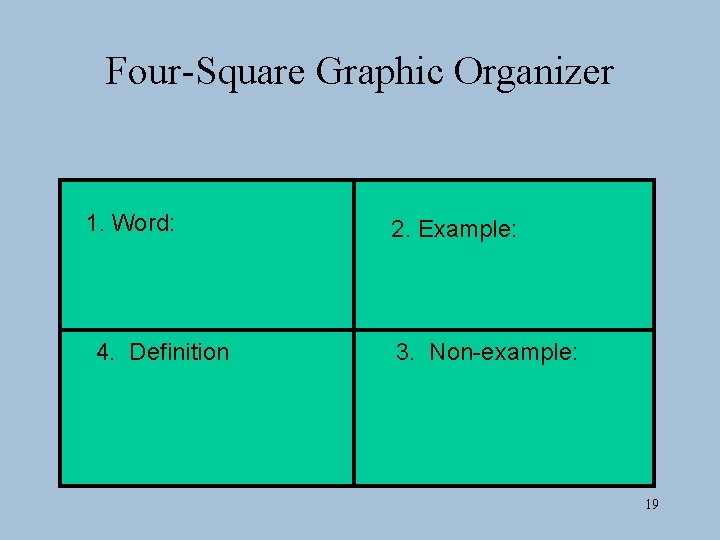
Four-Square Graphic Organizer 1. Word: 4. Definition 2. Example: 3. Non-example: 19

Four-Square Graphic Organizer – example 1. Word: semicircle 4. Definition 2. Example: 3. Non-example: A semicircle is half of a circle. 20

Matching Activity • In your Math groups, match the problem sets with the appropriate graphic organizer 21

Matching Activity • Which graphic organizer would be most suitable for showing these relationships? • Why did you choose this type? • Are there alternative choices? 22

Problem Set 1 Parallelogram Square Polygon Irregular polygon Isosceles Trapezoid Rhombus Quadrilateral Kite Trapezoid Rectangle 23

Problem Set 2 Counting Numbers: 1, 2, 3, 4, 5, 6, . . . Whole Numbers: 0, 1, 2, 3, 4, . . . Integers: . . . -3, -2, -1, 0, 1, 2, 3, 4. . . Rationals: 0, … 1/10, … 1/5, … 1/4, . . . 33, … 1/2, … 1 Reals: all numbers Irrationals: π, non-repeating decimal 24

Problem Set 3 Addition a+b a plus b sum of a and b Multiplication a times b axb a(b) ab Subtraction a–b a minus b a less b Division a/b a divided by b b) a 25

Problem Set 4 Use the following words to organize into categories and subcategories of Mathematics: NUMBERS, OPERATIONS, Postulates, RULE, Triangles, GEOMETRIC FIGURES, SYMBOLS, corollaries, squares, rational, prime, Integers, addition, hexagon, irrational, {1, 2, 3…}, multiplication, composite, m || n, whole, quadrilateral, subtraction, division. 26

Graphic Organizer Summary • GOs are a valuable tool for assisting students with LD in basic mathematical procedures and problem solving. • Teachers should: – Consistently, coherently, and creatively use GOs. – Employ teacher-directed and studentdirected approaches. – Address individual needs via curricular adaptations. 31

Resources • Maccini, P. , & Gagnon, J. C. (2005). Math graphic organizers for students with disabilities. Washington, DC: The Access Center: Improving Outcomes for all Students K-8. Available at http: //www. k 8 accescenter. org/training_resources/documents/Math. Grap hic. Org. pdf • Visual mapping software: Inspiration and Kidspiration (for lower grades) at http: /www. inspiration. com • Math Matrix from the Center for Implementing Technology in Education. Available at http: //www. citeducation. org/mathmatrix/ 32

Resources • Hall, T. , & Strangman, N. (2002). Graphic organizers. Wakefield, MA: National Center on Accessing the General Curriculum. Available at http: //www. cast. org/publications/ncac_go. html • Strangman, N. , Hall, T. , Meyer, A. (2003) Graphic Organizers and Implications for Universal Design for Learning: Curriculum Enhancement Report. Wakefield, MA: National Center on Accessing the General Curriculum. Available at http: //www. k 8 accesscenter. org/training_resources /udl/Graphic. Organizers. HTML. asp 33

How These Strategies Help Students Access Algebra • • Problem Representation Problem Solving (Reason) Self Monitoring Self Confidence 34

Recommendations: • Provide a physical and pictorial model, such as diagrams or hands-on materials, to aid the process for solving equations/problems. • Use think-aloud techniques when modeling steps to solve equations/problems. Demonstrate the steps to the strategy while verbalizing the related thinking. • Provide guided practice before independent practice so that students can first understand what to do for each step and then understand why. 35

Additional Recommendations: • Continue to instruct secondary math students with mild disabilities in basic arithmetic. Poor arithmetic background will make some algebraic questions cumbersome and difficult. • Allot time to teach specific strategies. Students will need time to learn and practice the strategy on a regular basis. 36

Wrap-Up • Questions 37

Closing Activity Principles of an effective lesson: Before the Lesson: • Review • Explain objectives, purpose, rationale for learning the strategy, and implementation of strategy During the Lesson: • Model the task • Prompt students in dialogue to promote the development of problem-solving strategies and reflective thinking • Provide guided and independent practice • Use corrective and positive feedback 38

Concepts for Developing a Lesson Grades K-2 • Use concrete materials to build an understanding of equality (same as) and inequality (more than and less than) • Skip counting Grades 3 - 5 • Explore properties of equality in number sentences (e. g. , when equals are added to equals the sums are equal) • Use physical models to investigate and describe how a change in one variable affects a second variable Grades 6 -8 • Positive and negative numbers (e. g. , general concept, addition, subtraction, multiplication, division) • Investigate the use of systems of equations, tables, and graphs to represent mathematical relationships 39