Graphene quantum Hall effect In the effectivemass picture

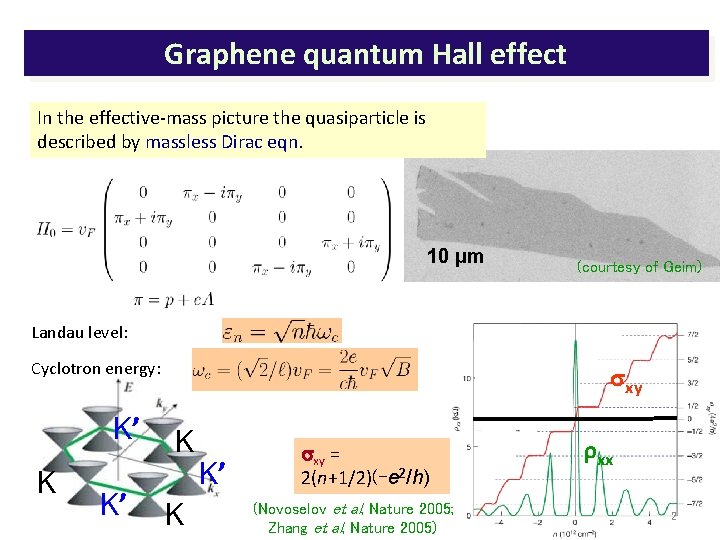
Graphene quantum Hall effect In the effective-mass picture the quasiparticle is described by massless Dirac eqn. 10 μm (courtesy of Geim) Landau level: Cyclotron energy: K’ K K’ sxy K K K’ sxy = 2(n+1/2)(-e 2/h) (Novoselov et al, Nature 2005; Zhang et al, Nature 2005) rxx 2

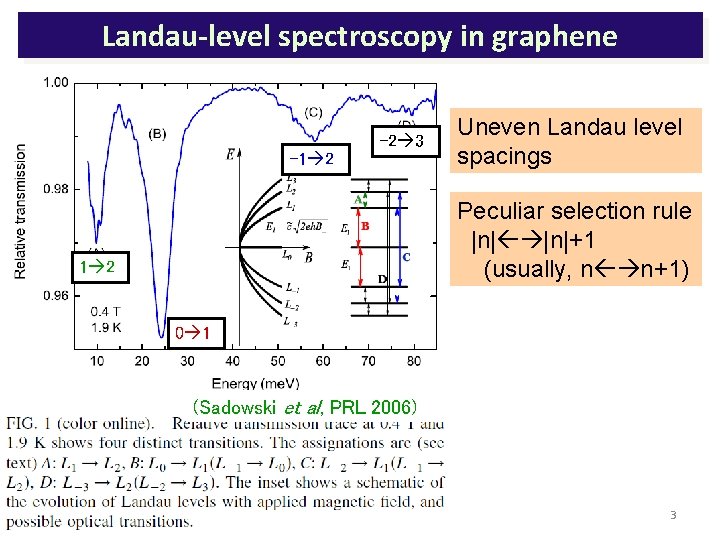
Landau-level spectroscopy in graphene -2 3 -1 2 Uneven Landau level spacings Peculiar selection rule |n|+1 (usually, n n+1) 1 2 0 1 (Sadowski et al, PRL 2006) 3

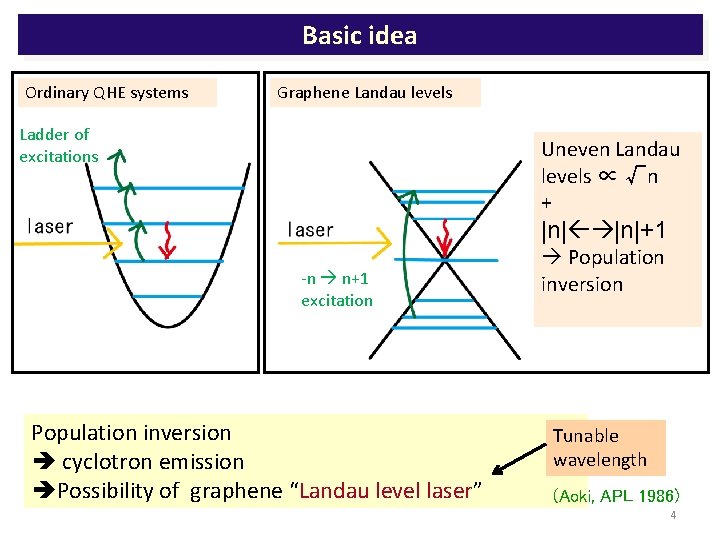
Basic idea Ordinary QHE systems Graphene Landau levels Ladder of excitations Uneven Landau levels ∝ √n + |n|+1 -n n+1 excitation Population inversion cyclotron emission Possibility of graphene “Landau level laser” Population inversion Tunable wavelength (Aoki, APL 1986) 4

Optical conductivity s(w): method Green’ s f SCBA s(w) Singular DOS makes the calculation difficult. Optical conductivity is calculated from Kubo formula : Level broadening by impurity is considered through Born approximation with self-consistent Green’s function. current matrix elements short range Impurity potential Solve self-consistently by numerical method (Ando, Zheng & Ando, PRB 2002) Cf. Gusynin et al. (PRB 2006) no self-consistent treatment of impurity scattering 5

Optical conductivity : result 0 1 1 2 -1 2 higher T (Sadowski et al, 2006) 6

Density of states suitable for radiation Uneven Landau levels ∝ rapid decay excitation Population inversion Cyclotron radiation Impurity n=0 Landaubroadening level stands alone, while others form continuum spectra Population inversion is expected between n=0 and continuum. photoemission vs other relaxation processes (phonon) 7

Relaxation process : photon emission Spontaneous photon emission rate is calculated from Fermi’s golden rule. Singular B dependence of Dirac quasiparticle in graphene Magnetic field: 1 T Orders of magnitude more efficient photoemission in graphene 8

Competing process : phonon emission q Ordinary QHE system Chaubet et al. , PRB 1995, 1998 discussed phonon emission is the main relaxation channel. Graphene Also obtained from golden rule and factor with and , phonon emission is exponentially small in graphene as well. Effect of phonon ^ 2 DEG same order as photoemission in conventional QHE (Chaubet et al. PRB 1998) 2 DEG Phonon ^ 2 DEG Graphene is only one atom thick phonon does not compete with photoemission. However, atomic phonon modes ^ graphene will have to be examined Wavefunction with a finite thickness 9

2 D electron gas ρxy ρxx B 2 D EG (Paalanen et al, 1982) 10

THz spectroscopy of 2 DEG Ellipticity Faraday rotation Resonance structure at cyclotron energy (Sumikura et al, JJAP, 2007) 11

Motivation ●conventional results - Hall conductivity quantization at w=0 - Faraday rotation measurement in finite w Only Drude form treatment ● How peculiar can optical Hall conductivity sxy (e. F, w) be? ● Is ac QHE possible? (O'Connell et al, PRB 1982) Calculating sxy (e. F, w) from … ● Kubo formula ● Self-consistent Born approximation 12

sxy (w) in Ga. As ● 3 D plot of sxy (e. F, w) against Fermi energy and frequency sxy (w) Hall step still remains in ac regime sxy (w) w=0. 4 w. C e. F sxy (w) w w e. F Resonance at cyclotron frequency 13

sxy (w) in graphene ● sxy (e. F, w) of graphene 電子正孔対称 w=0 e. F sxy (w) Resonance at cyclotron frequency w e. F Reflecting massless Dirac DOS structure Hall step remains w 14

Consideration with Kubo formula ●Why does Hall step remain in ac region? ●How robust is it? Clean ordinary QHE system Hall step structure in clean system (not disturbed so much by impurity) □ • • • Future problem Effect of long-range impurity Localization and delocalization in ac field Relation to topological arguement THz Hall 効果 (Peng et al, PRB 1991) ではacの取り扱いが不十分 15