Graph Visualization and Navigation in Information Visualization a

Graph Visualization and Navigation in Information Visualization: a Survey Ivan Herman, Guy Melançon, and M. Scott Marshall (Presentation: Anne Denton March 6, 2003)

Outline n n Graph drawing and graph visualization Graph layout Navigation of large graphs Reorganization of data: Clustering

Information Visualization vs. Graph Drawing n n n Old topic, many books, etc. May have other goals than visualization n E. g. VLSI design Graph Visualization n Size key issue Usability requires nodes to be discernable Navigation considered

Node Information? n n n Sometimes a “size” or “importance” is represented Navigational systems may have links to data Glyphs? n n Mentioned as representation of higher levels in hierarchical clustering Focus on structure-based properties n Application independent

Examples n n n Class browsers Entity relationship diagrams Real-time systems (state transition diagrams) VLSI circuit design (circuit schematics rather than actual design) Document management system n n Web-navigation Virtual Reality (scene graph)

History of Graph Drawing n n n Euler used a drawing to solve the Königsberger Brückenproblem (1736) Symposia on Graph Drawing initiated 1992 Issues n Planarity n n No edges cross in 2 D Aesthetic rules n n n Edges should have same length Edges should be straight lines Isomorphic substructures displayed equivalently

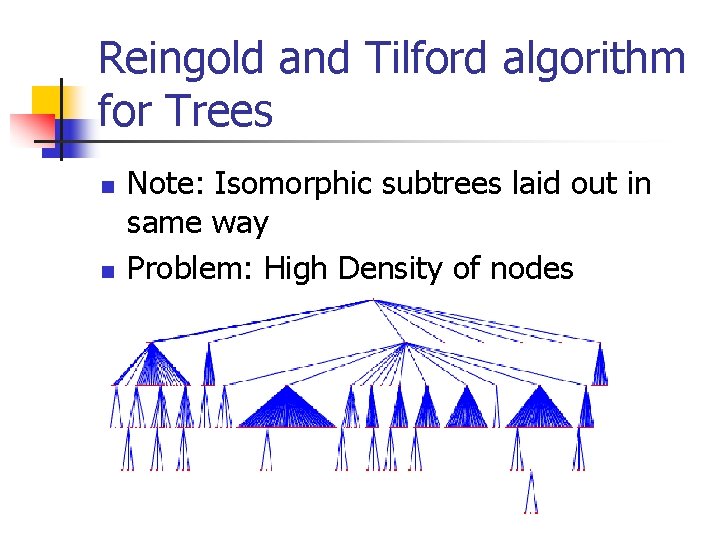
Reingold and Tilford algorithm for Trees n n Note: Isomorphic subtrees laid out in same way Problem: High Density of nodes

Tasks Related to Graph Drawing Layering a graph n Turning graph into directed acyclic graph n Planarizing (achieve that no edges cross) n Minimizing area n Minimizing number of bends in edges But n Algorithms too complex for large graphs n

Problem: Size n n n Previous example: few hundred nodes How about thousands of nodes? Solutions n n 3 D Non-Euclidean geometry (e. g. , hyperbolic geometry) Reduce size Show part only / blow up part

Other problems related to Navigation n Predictability n n n Two different runs on similar trees should lead to similar results Traditional layouts next page are predicatable Time Complexity n Real time interaction

Traditional Tree Layouts n n Classical layout on earlier slide H-tree layout: best for balanced trees Radial view Balloon view: related to 3 -d cone tree

Tree-Map n Useful for information visualization because area is meaningful Example: n Problem: Tree structure less clear n http: //www. smartmoney. com/marketmap n Size represents market share n Color represents performance n More information available through clicking

Layout of Directed Graphs n Layering (http: //www. csus, yk, ue/staff/Nikola. Nikolov/#phd)

Spring Layout n n Force directed Nodes are modeled as physical bodies that are connected through springs (edges) High time complexity: > O(N 3) Not predictable

Spanning Trees n Further conclusions from size n n n Don’t insist on planarity Don’t worry about edge crossings Graph can be visualized through minimum spanning tree n n Additional edges added later Very common technique Helps with predictability Visualization depends on starting point

3 D Techniques n Benefits n n n “Gaining more space” Human familiarity with 3 D Problems n n n 2 D displays Missing motion and stereo cues May be solved by better technology

Examples of 3 D Techniques n n 3 D version of a radial tree Info cube

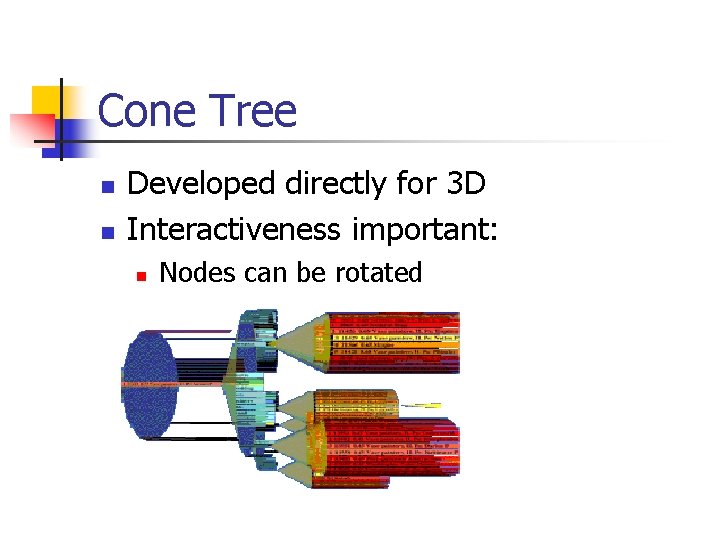
Cone Tree n n Developed directly for 3 D Interactiveness important: n Nodes can be rotated

Fly-Through of 2 D Representation n SGI File System Navigator Size represents file size Similar: n Perspective wall

Hyperbolic Layout n n n Mainly used for trees E. g. web-content viewers 2 D or 3 D Similar to fish-eye lense Possibility of interacting with large trees

EBI Hyperbolic Viewers n 2 D example applets http: //industry. ebi. ac. uk/~alan/components/example 1. html http: //www. inxight. com/map n 3 D image

Hyperbolic Viewer Concepts n n n For a given point and non-intersecting line: many parallel lines through point Segments that are congruent in the hyperbolic sense are exponentially smaller in the Euclidean sense when approaching the perimeter Projective Klein model n n n Straight lines Suitable for 4 x 4 matrix-based graphics Conformal or Poincaré model n n n Straight lines drawn as arcs Angles are drawn correctly in Euclidean sense Computationally more demanding

Klein Model vs. Poincare Model T. Munzner, P. Burchard, “Visualizing the structure of the World Wide Web in 3 D Hyperbolic Space, ” Proceedings of the VRML Symposium, pp 33 -38, 1995. Klein Model Poincare Model

Simple Tree Construction Algorithm Node P with wedge QPR n Subtrees start at P 1, P 2, and P 3 Euclidean Hyperbolic n

Navigation and Interaction n Zoom and pan n n Geometric zooming n n Zoom for graphs exact, not pixel-based (adjustment of screen transformations) Simple blow-up Semantic zooming n n Content changes Clustering

Problem with Combination of Zoom and Pan n n Assume zoom and pan independent Objects may temporarily move away Solution: Spacescale diagram (Semantic zoom: picture differs for each level)

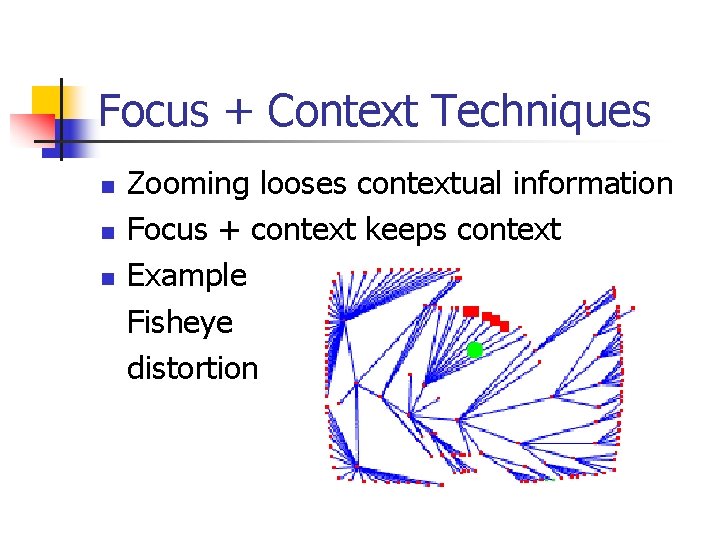
Focus + Context Techniques n n n Zooming looses contextual information Focus + context keeps context Example Fisheye distortion

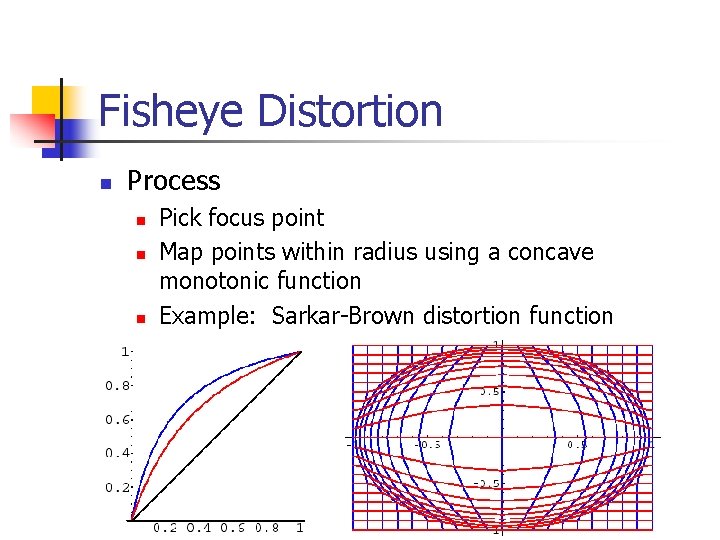
Fisheye Distortion n Process n n n Pick focus point Map points within radius using a concave monotonic function Example: Sarkar-Brown distortion function

Problem with Fisheye n Distortion should also be applied to links n n Alternative n n n Prohibitively slow (polyline) Continue using lines Can result in unintended line crossings Other Alternative n Þ Þ Combine layout with focus+context Hyperbolic viewer Other combinations possible (e. g. balloon view with focus-dependent radii) but not yet done

Incremental Exploration and Navigation For very large graphs (e. g. Internet) n Small portion displayed n Other parts displayed as needed n Displayed graph small Þ Layout and interaction times may be small Example not from the paper http: //touchgraph. sourceforge. net/ (Force-directed? Note how animation helps adjusting to new layout) n

Clustering n Structure-based clustering n n Þ n Most common in graph visualization Often retain structure of graph Useful for user orientation Content-based clustering n n Application specific Can be used for n n Filtering: de-emphasis or removal of elements from view Search: emphasis of an element or group of elements

Clustering continued n n n Common goal n Finding disjoint clusters Clumping n Finding overlapping clusters Common technique n Least number of edges between neighbors (Ratio Cut technique in VLSI design)

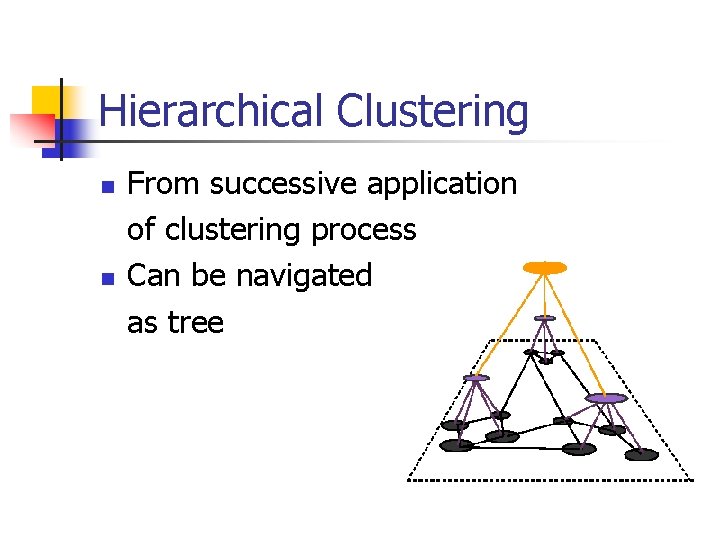
Hierarchical Clustering n n From successive application of clustering process Can be navigated as tree

Visualization of higher levels n Herman et al. say glyphs are used (? ) P. Eades, Q. Feng, “Multilevel Visualization of Clustered Graphs, ” Lecture Notes in Computer Science”, 1190, pp 101 -112, 1997

Node Metrics n n n Measure abstract feature Give ranking Edge metrics also possible Structure-based or content-based Examples n n n Application-specific weight Degree of the node “Degree of Interest” (Furnas)

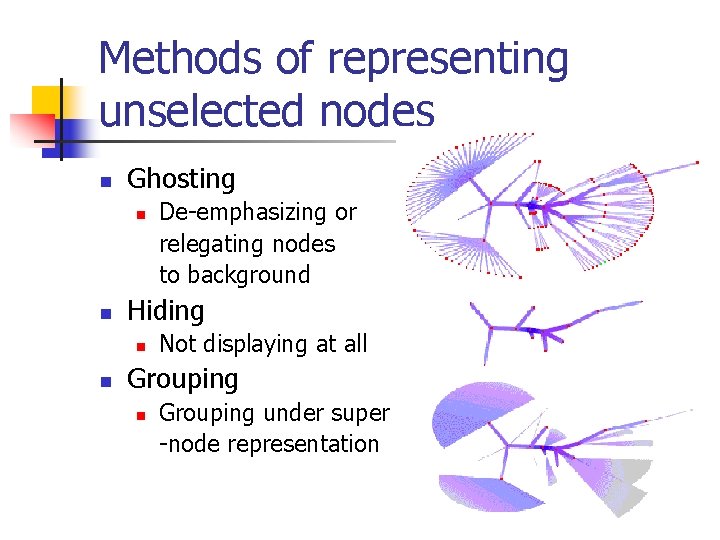
Methods of representing unselected nodes n Ghosting n n Hiding n n De-emphasizing or relegating nodes to background Not displaying at all Grouping n Grouping under super -node representation

Summary n Graph drawing and graph visualization n n Graph layout n n Much is known from graph drawing Navigation of large graphs n n Overlap but different goals and problems Key tool in dealing with size Reorganization of data: Clustering n Still much to be done