Graph Traversals DepthFirst Traversals Algorithms Example Implementation BreadthFirst

Graph Traversals • Depth-First Traversals. – Algorithms. – Example. – Implementation. • Breadth-First Traversal. – The Algorithm. – Example. – Implementation. • Topological Sort • Review Questions.

Depth-First Traversal Algorithm • In this method, After visiting a vertex v, which is adjacent to w 1, w 2, w 3, . . . ; Next we visit one of v's adjacent vertices, say w 1. Next, we visit all vertices adjacent to w 1 before coming back to w 2, etc. • Must keep track of vertices already visited to avoid cycles. • The method can be implemented using recursion or iteration. • The iterative preorder depth-first algorithm is: 1 push the starting vertex onto the stack 2 while(stack is not empty){ 3 pop a vertex off the stack, call it v 4 if v is not already visited, visit it 5 push vertices adjacent to v, not visited, onto the stack 6 } • Note: Adjacent vertices can be pushed in any order; but to obtain a unique traversal, we will push them in reverse alphabetical order.

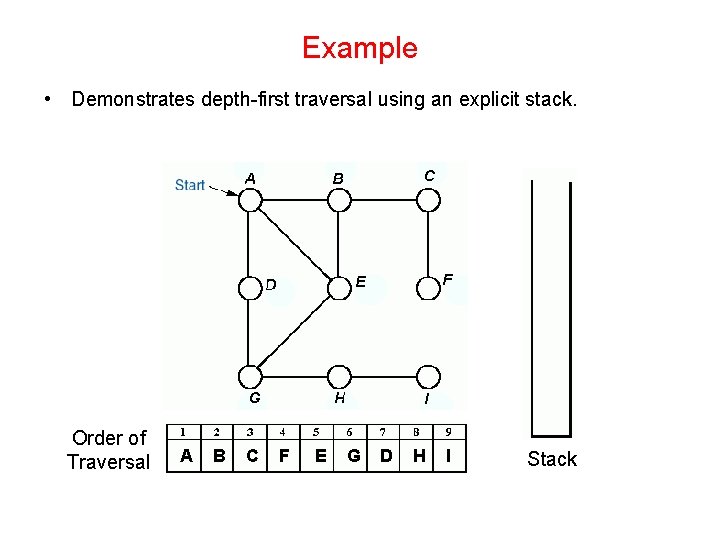
Example • Demonstrates depth-first traversal using an explicit stack. Order of Traversal A B C F E G D H I Stack

Recursive preorder Depth-First Traversal Implementation dfs. Preorder(v){ visit v; for(each neighbour w of v) if(w has not been visited) dfs. Preorder(w); } • The following is the code for the recursive preorder. Depth. First. Traversal method of the Abstract. Graph class: public void preorder. Depth. First. Traversal(Visitor visitor, Vertex start) { boolean visited[] = new boolean[number. Of. Vertices]; for(int v = 0; v < number. Of. Vertices; v++) visited[v] = false; preorder. Depth. First. Traversal(visitor, start, visited); }

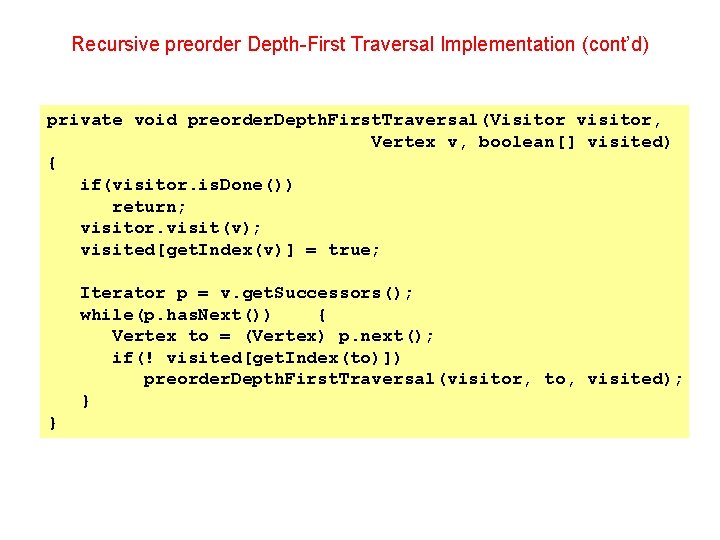
Recursive preorder Depth-First Traversal Implementation (cont’d) private void preorder. Depth. First. Traversal(Visitor visitor, Vertex v, boolean[] visited) { if(visitor. is. Done()) return; visitor. visit(v); visited[get. Index(v)] = true; Iterator p = v. get. Successors(); while(p. has. Next()) { Vertex to = (Vertex) p. next(); if(! visited[get. Index(to)]) preorder. Depth. First. Traversal(visitor, to, visited); } }

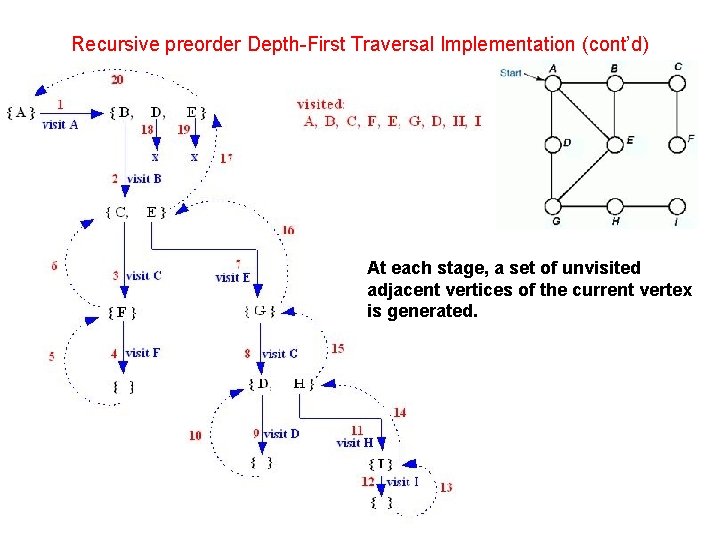
Recursive preorder Depth-First Traversal Implementation (cont’d) At each stage, a set of unvisited adjacent vertices of the current vertex is generated.

Recursive postorder Depth-First Traversal Implementation dfs. Postorder(v){ mark v; for(each neighbour w of v) if(w is not marked) dfs. Postorder(w); visit v; } • The following is the code for the recursive postorder. Depth. First. Traversal method of the Abstract. Graph class: public void postorder. Depth. First. Traversal(Visitor visitor, Vertex start) { boolean visited[] = new boolean[number. Of. Vertices]; for(int v = 0; v < number. Of. Vertices; v++) visited[v] = false; postorder. Depth. First. Traversal(visitor, start, visited); }

Recursive postorder Depth-First Traversal Implementation (cont’d) private void postorder. Depth. First. Traversal( Visitor visitor, Vertex v, boolean[] visited) { if(visitor. is. Done()) return; // mark v visited[get. Index(v)] = true; Iterator p = v. get. Successors(); while(p. has. Next()){ Vertex to = (Vertex) p. next(); if(! visited[get. Index(to)]) postorder. Depth. First. Traversal(visitor, to, visited); } // visit v visitor. visit(v); }

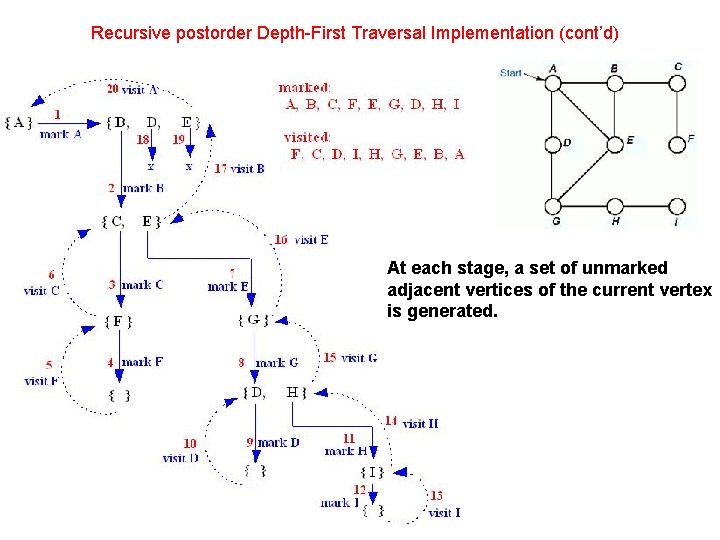
Recursive postorder Depth-First Traversal Implementation (cont’d) At each stage, a set of unmarked adjacent vertices of the current vertex is generated.

Breadth-First Traversal Algorithm • In this method, After visiting a vertex v, we must visit all its adjacent vertices w 1, w 2, w 3, . . . , before going down next level to visit vertices adjacent to w 1 etc. • The method can be implemented using a queue. • A boolean array is used to ensure that a vertex is enqueued only once. 1 enqueue the starting vertex 2 while(queue is not empty){ 3 dequeue a vertex v from the queue; 4 visit v. 5 enqueue vertices adjacent to v that were never enqueued; 6 } • Note: Adjacent vertices can be enqueued in any order; but to obtain a unique traversal, we will enqueue them in alphabetical order.

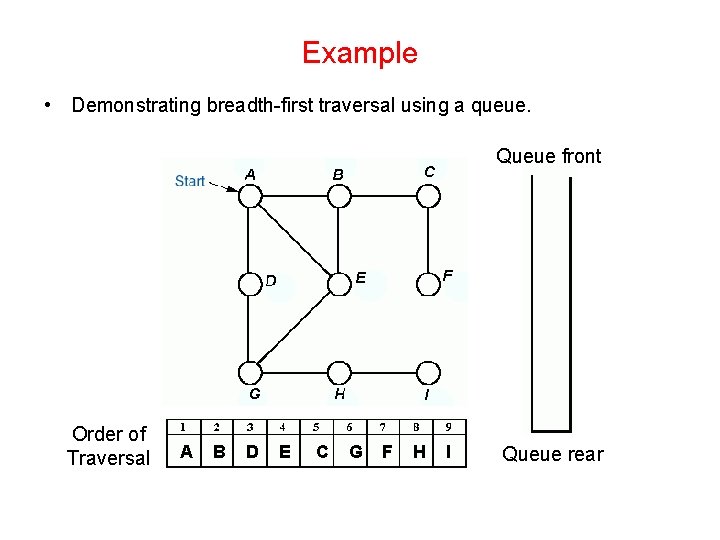
Example • Demonstrating breadth-first traversal using a queue. Queue front Order of Traversal A B D E C G F H I Queue rear

Breadth-First Traversal Implementation public void breadth. First. Traversal(Visitor visitor, Vertex start){ boolean enqueued[] = new boolean[number. Of. Vertices]; for(int i = 0; i < number. Of. Vertices; i++) enqueued[i] = false; Queue queue = new Queue. As. Linked. List(); enqueued[get. Index(start)] = true; queue. enqueue(start); //enqueue the starting vertex while(!queue. is. Empty() && !visitor. is. Done()) { Vertex v = (Vertex) queue. dequeue(); //dequeue a vertex v from the queue visitor. visit(v); Iterator it = v. get. Successors(); while(it. has. Next()) { Vertex to = (Vertex) it. next(); int index = get. Index(to); if(!enqueued[index]) { enqueued[index] = true; queue. enqueue(to); } } // visit v //enqueue vertices adjacent to v that were never enqueued

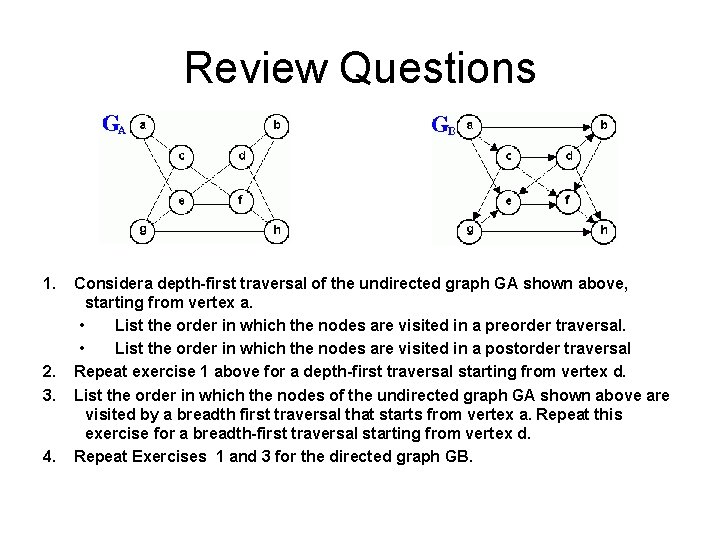
Review Questions 1. 2. 3. 4. Considera depth-first traversal of the undirected graph GA shown above, starting from vertex a. • List the order in which the nodes are visited in a preorder traversal. • List the order in which the nodes are visited in a postorder traversal Repeat exercise 1 above for a depth-first traversal starting from vertex d. List the order in which the nodes of the undirected graph GA shown above are visited by a breadth first traversal that starts from vertex a. Repeat this exercise for a breadth-first traversal starting from vertex d. Repeat Exercises 1 and 3 for the directed graph GB.

Topological Sort • Introduction. • Definition of Topological Sort. • Topological Sort is Not Unique. • Topological Sort Algorithm. • An Example. • Implementation. • Review Questions.

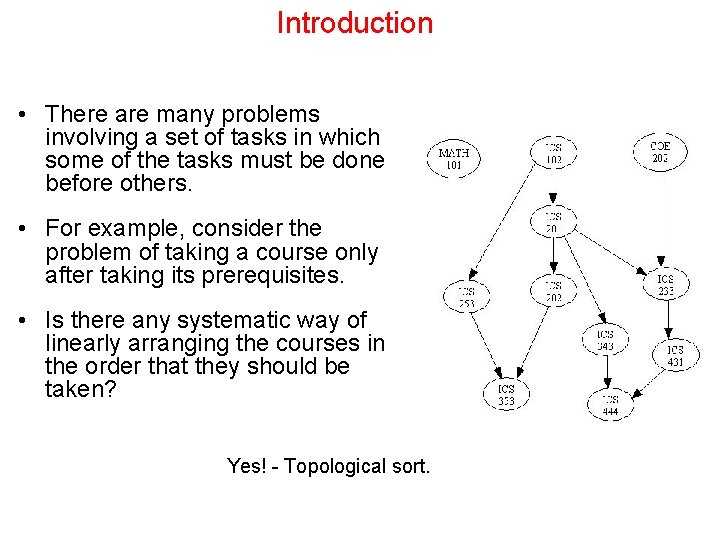
Introduction • There are many problems involving a set of tasks in which some of the tasks must be done before others. • For example, consider the problem of taking a course only after taking its prerequisites. • Is there any systematic way of linearly arranging the courses in the order that they should be taken? Yes! - Topological sort.

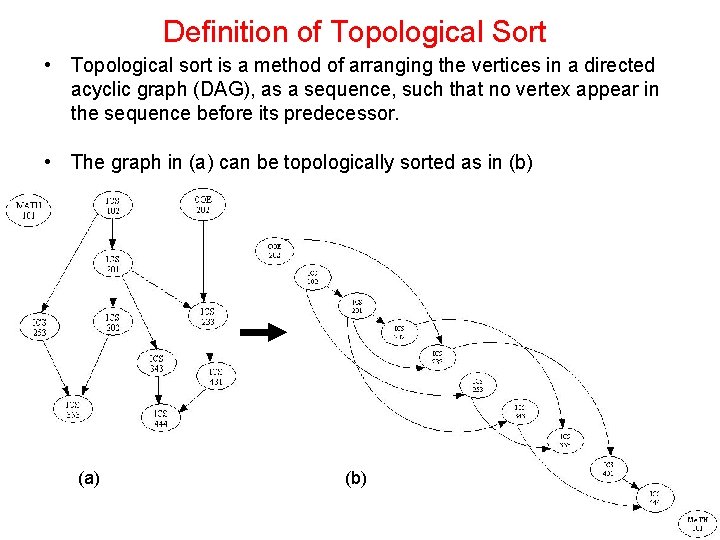
Definition of Topological Sort • Topological sort is a method of arranging the vertices in a directed acyclic graph (DAG), as a sequence, such that no vertex appear in the sequence before its predecessor. • The graph in (a) can be topologically sorted as in (b) (a) (b)

Topological Sort is not unique • Topological sort is not unique. • The following are all topological sort of the graph below: s 1 = {a, b, c, d, e, f, g, h, i} s 2 = {a, c, b, f, e, d, h, g, i} s 3 = {a, b, d, c, e, g, f, h, i} s 4 = {a, c, f, b, e, h, d, g, i} etc.

Topological Sort Algorithm • One way to find a topological sort is to consider in-degrees of the vertices. • The first vertex must have in-degree zero -- every DAG must have at least one vertex with in-degree zero. • The Topological sort algorithm is: int topological. Order. Traversal( ){ int num. Visited. Vertices = 0; while(there are more vertices to be visited){ if(there is no vertex with in-degree 0) break; else{ select a vertex v that has in-degree 0; visit v; num. Visited. Vertices++; delete v and all its emanating edges; } } return num. Visited. Vertices; }

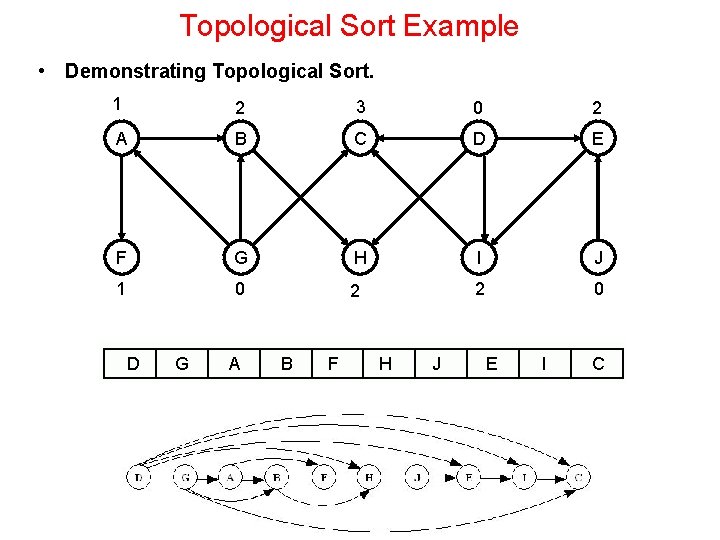
Topological Sort Example • Demonstrating Topological Sort. 1 2 3 0 2 A B C D E F G H I J 1 0 2 2 0 D G A B F H J E I C

Implementation of Topological Sort • The algorithm is implemented as a traversal method that visits the vertices in a topological sort order. • An array of length |V| is used to record the in-degrees of the vertices. Hence no need to remove vertices or edges. • A priority queue is used to keep track of vertices with in-degree zero that are not yet visited. public int topological. Order. Traversal(Visitor visitor){ int num. Vertices. Visited = 0; int[] in. Degree = new int[number. Of. Vertices]; for(int i = 0; i < number. Of. Vertices; i++) in. Degree[i] = 0; Iterator p = get. Edges(); while (p. has. Next()) { Edge edge = (Edge) p. next(); Vertex to = edge. get. To. Vertex(); in. Degree[get. Index(to)]++; }

Implementation of Topological Sort Binary. Heap queue = new Binary. Heap(number. Of. Vertices); p = get. Vertices(); while(p. has. Next()){ Vertex v = (Vertex)p. next(); if(in. Degree[get. Index(v)] == 0) queue. enqueue(v); } while(!queue. is. Empty() && !visitor. is. Done()){ Vertex v = (Vertex)queue. dequeue. Min(); visitor. visit(v); num. Vertices. Visited++; p = v. get. Successors(); while (p. has. Next()){ Vertex to = (Vertex) p. next(); if(--in. Degree[get. Index(to)] == 0) queue. enqueue(to); } } return num. Vertices. Visited; }

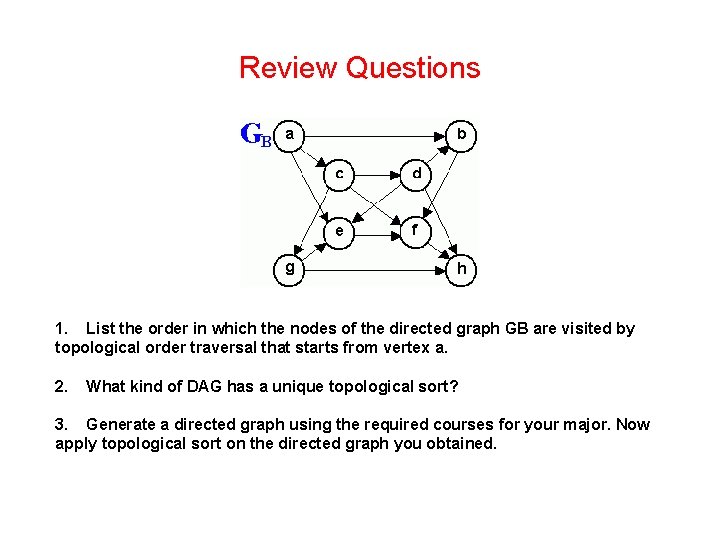
Review Questions 1. List the order in which the nodes of the directed graph GB are visited by topological order traversal that starts from vertex a. 2. What kind of DAG has a unique topological sort? 3. Generate a directed graph using the required courses for your major. Now apply topological sort on the directed graph you obtained.