Graph Theory Traveling Salesman Problems Nearest Neighbor Method

Hamilton Paths & Circuits Using the Nearest Neighbor Method to solve a traveling salesman problem.

Hamilton Paths & Circuits The brute force method becomes very taxing as your problems contain more and more vertices. The Nearest Neighbor Method will come to an approximate solution much faster, but using the nearest neighbor method may not yield the true optimal circuit. For a true optimal solution, brute force method must be used.

Hamilton Paths & Circuits Steps: (to find an approximate solution to a traveling salesman problem) 1. Represent the problem with a complete weighted graph. 2. Identify the starting vertex. 3. Travel along the least expensive (or shortest) path to the ext vertex. Circle the cost. 4. Repeat step 3 without returning to a vertex for a second ime until you have visited all vertices and finally eturned to the starting vertex.

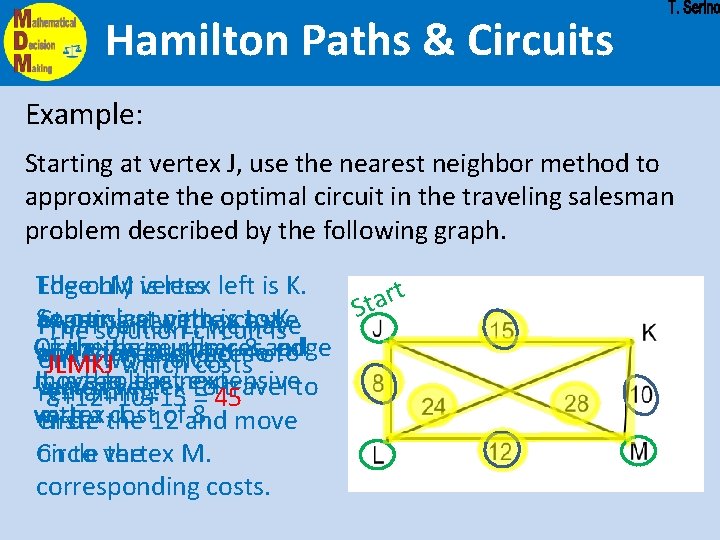
Hamilton Paths & Circuits Example: Starting at vertex J, use the nearest neighbor method to approximate the optimal circuit in the traveling salesman problem described by the following graph. The Edgeonly LM vertex is less left is K. t r a t S So our last path is to K expensive with a cost Starting at vertex we From vertex L, circuit we J, have The solution is Of Circle the three number choices, 8 of and edge and then back home to of 12. have three choices only two choices JLMKJ which costs JL move is the to. J. least the next expensive vertex which vertex travel to remaining. 8+12+10+15 to = 45 with vertex, cost L. 12 ofand 8. move Circle first. a the Circle the M. on to vertex corresponding costs.

Hamilton Paths & Circuits Try this: Starting at vertex a, use the nearest neighbor method to approximate the optimal circuit in the traveling salesman problem described by the following graph. Do not go on until you have Do NOT go on until you have competed the problem on completed the problem! your own.

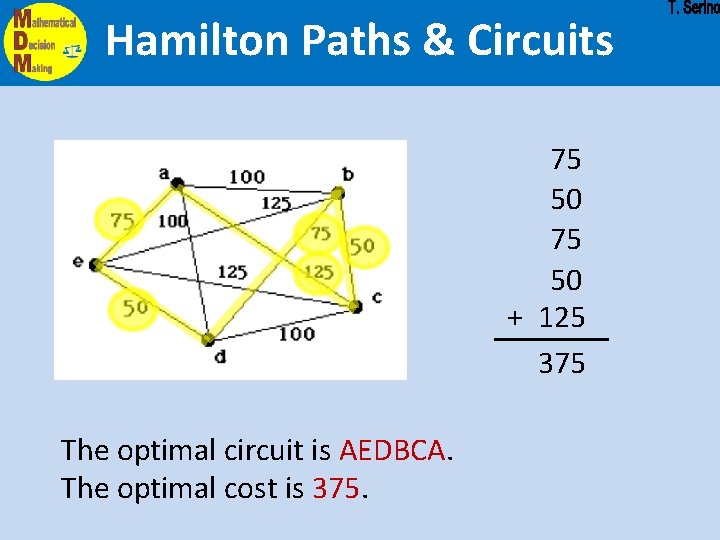
Hamilton Paths & Circuits 75 50 + 125 375 The optimal circuit is AEDBCA. The optimal cost is 375.