Graph theory identity assignment x x DSP graphs

Why is graph theory useful ? DSP graphs capture both • algorithms and •

Basic blocks yn = xn - xn-1 yn = a 0 xn + a

Basic MA blocks yn = a 0 xn + a 1 xn-1 4

General MA we would like to build tapped delay line = FIFO but we

General MA (cont. ) Instead we can build MACs We still have tapped delay

General MA (cont. ) There are other ways to implement the same MA still

Basic AR block One way to implement Note the feedback Whenever there is a

General AR filters There are many ways to implement the general AR Note the

ARMA filters The straightforward implementation : Note L+M memory points Now we can demonstrate

ARMA filters (cont. ) We can commute the MA and AR filters (any 2

ARMA filters (cont. ) So we can use only one point And eliminate redundant

Allowed transformations 1. Geometrical transformations that do no change topology 2. Commutation of any

Slides: 13

Download presentation

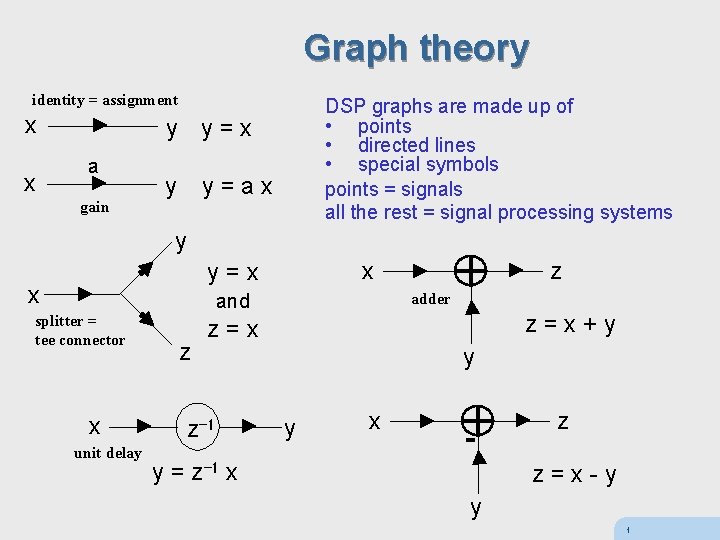
Graph theory identity = assignment x x DSP graphs are made up of • points • directed lines • special symbols points = signals all the rest = signal processing systems y y=x a gain y y=ax y x y=x x splitter = tee connector x unit delay adder and z z z=x+y z=x z-1 y y x - y = z-1 x z z=x-y y 1

Why is graph theory useful ? DSP graphs capture both • algorithms and • data structures Their meaning is purely topological Graphical mechanisms for simplifying (lowering MIPS or memory) Four basic transformations 1. Topological (move points around) 2. Commutation of filters (any two filters commute!) 3. Unification of identical signals (points) and removal of redundant branches 4. Transposition theorem 2

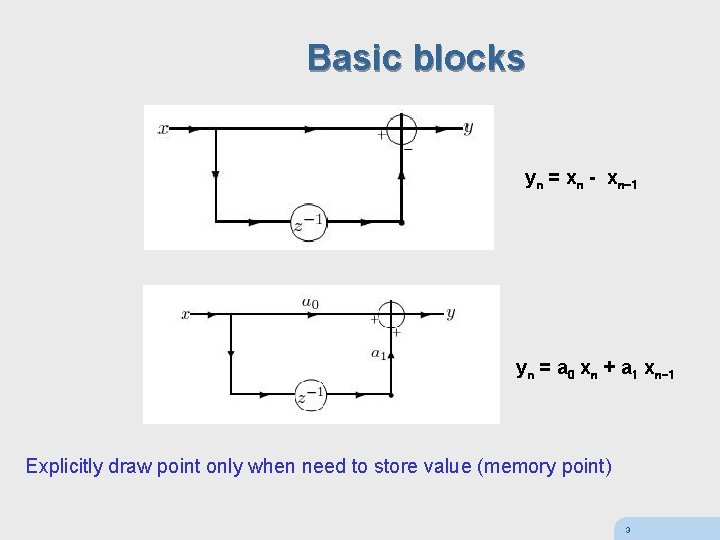
Basic blocks yn = xn - xn-1 yn = a 0 xn + a 1 xn-1 Explicitly draw point only when need to store value (memory point) 3

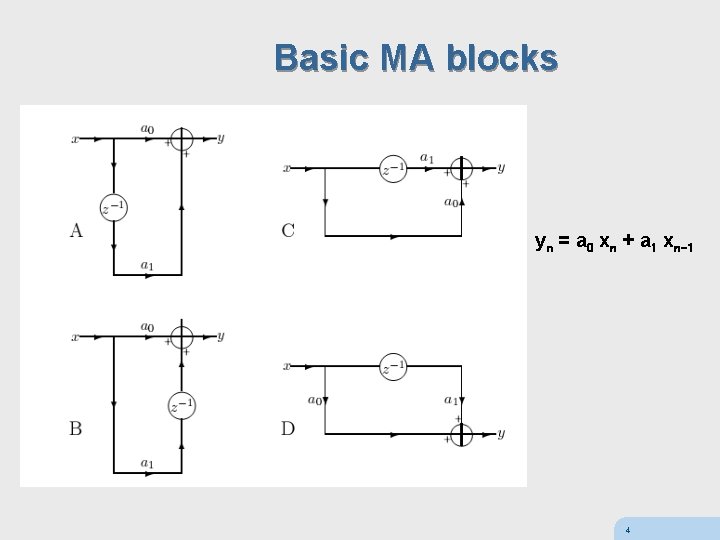
Basic MA blocks yn = a 0 xn + a 1 xn-1 4

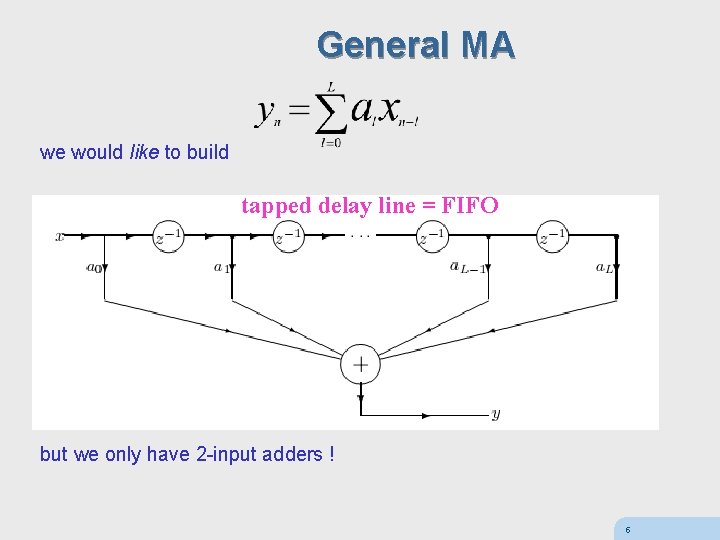
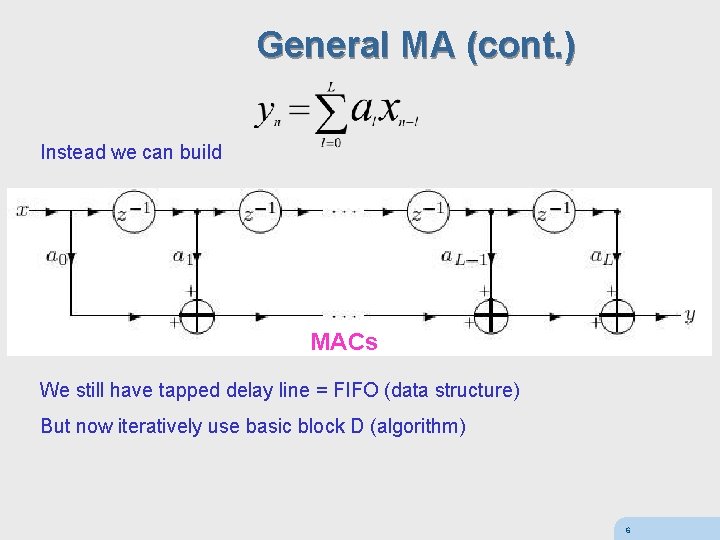
General MA we would like to build tapped delay line = FIFO but we only have 2 -input adders ! 5

General MA (cont. ) Instead we can build MACs We still have tapped delay line = FIFO (data structure) But now iteratively use basic block D (algorithm) 6

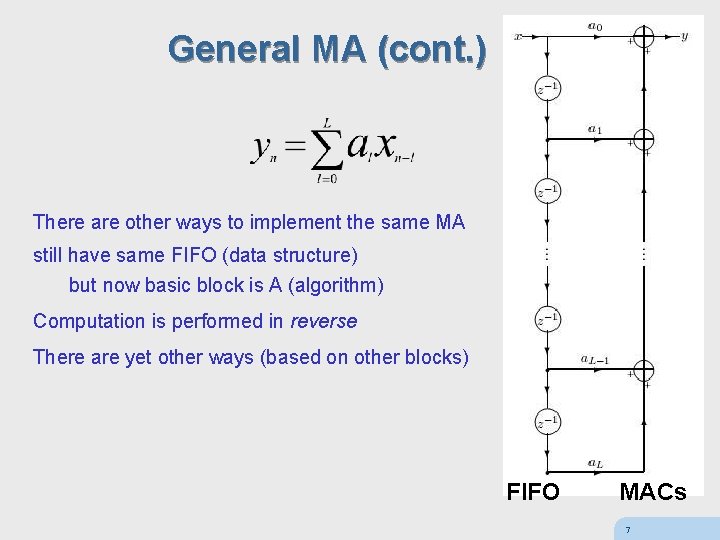
General MA (cont. ) There are other ways to implement the same MA still have same FIFO (data structure) but now basic block is A (algorithm) Computation is performed in reverse There are yet other ways (based on other blocks) FIFO MACs 7

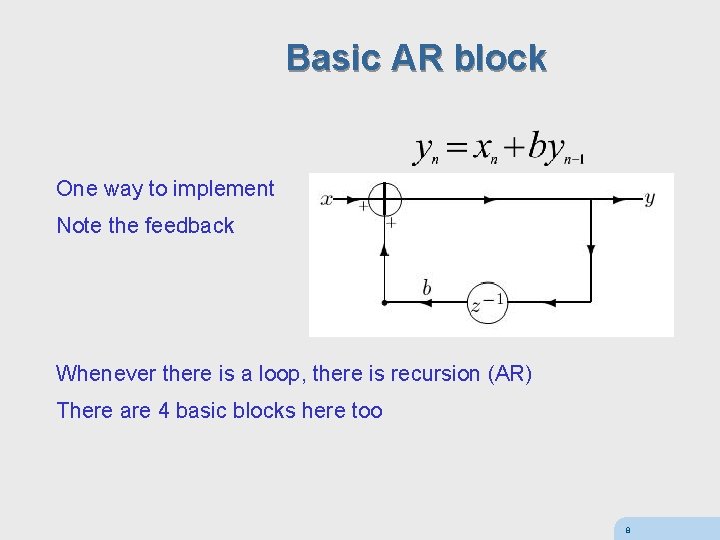
Basic AR block One way to implement Note the feedback Whenever there is a loop, there is recursion (AR) There are 4 basic blocks here too 8

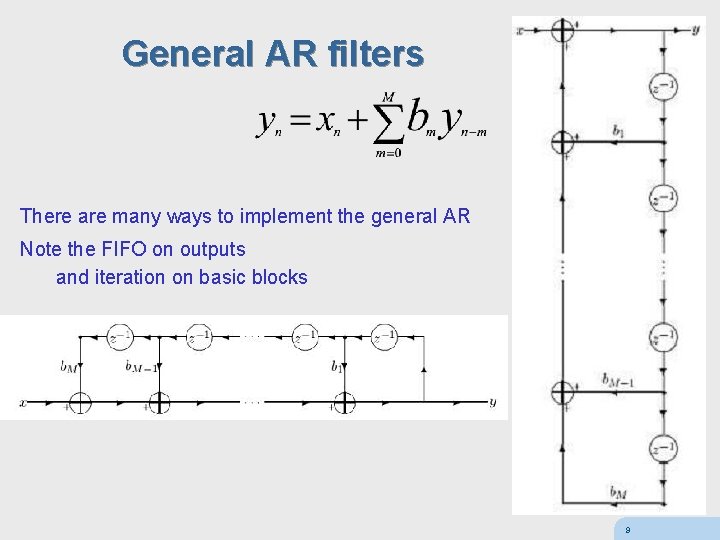
General AR filters There are many ways to implement the general AR Note the FIFO on outputs and iteration on basic blocks 9

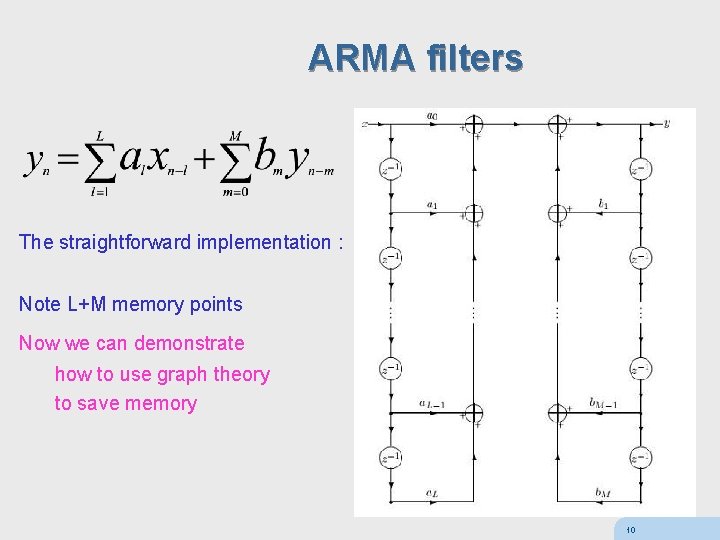
ARMA filters The straightforward implementation : Note L+M memory points Now we can demonstrate how to use graph theory to save memory 10

ARMA filters (cont. ) We can commute the MA and AR filters (any 2 filters commute) Now that there are points representing the same signal ! Assume that L=M (w. o. l. g. ) 11

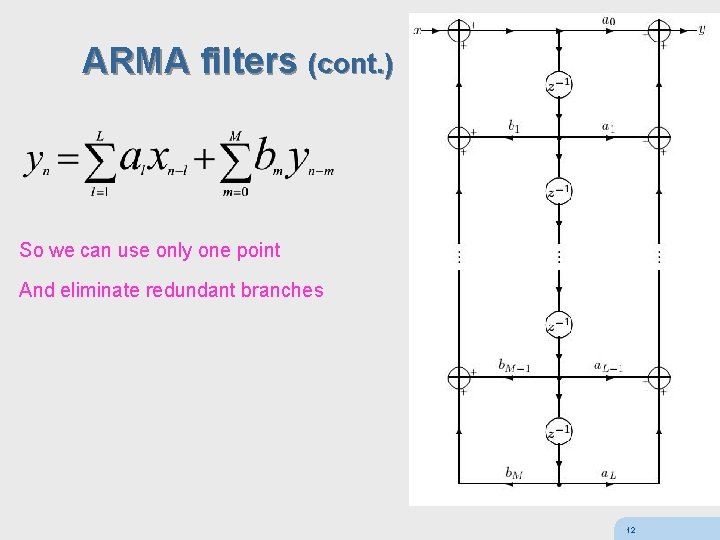
ARMA filters (cont. ) So we can use only one point And eliminate redundant branches 12

Allowed transformations 1. Geometrical transformations that do no change topology 2. Commutation of any two filters 3. Unification of identical points (signals) and elimination of redundant branches 4. Transposition theorem n n exchange input and output reverse all arrows replace adders with splitters replace splitters with adders 13