Graph Theory Graph Colorings Coloring Basics kcoloring of

Graph Theory Graph Colorings

Coloring Basics • k-coloring of the vertices of a graph is the number of colors needed so that no adjacent vertices are the same color, then it is k-colorable • Only considering vertex colorings, not edge colorings • Chromatic number: smallest integer such that a graph is kcolorable, or the smallest number of colors needed to color a graph

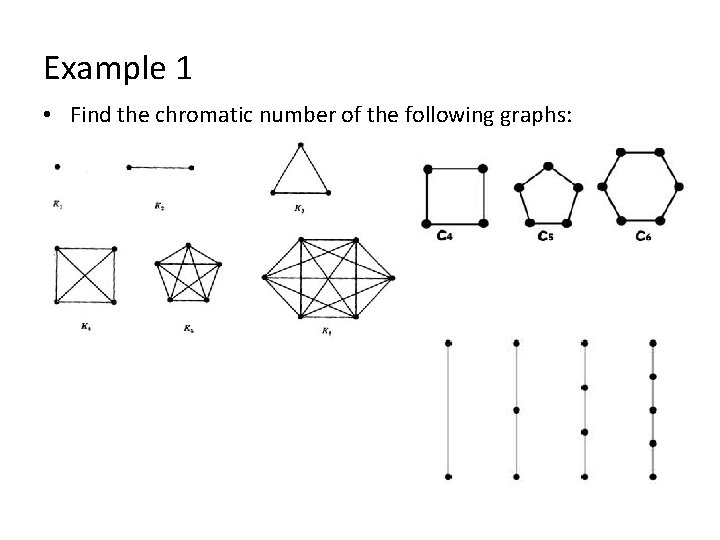
Example 1 • Find the chromatic number of the following graphs:

Example 2 • In assigning frequencies to cellular phones, a zone gets a frequency to be used by all vehicles in the zone. Two zones that interfere (because of proximity or meteorological reasons) must get different frequencies. How many different frequencies are required if there are six zones, a, b, c, d, e, f and zone a interferes with zone b; zone b interferes with a, c, and d; c interferes with b, d, and e; d interferes with b, c, and e; e interferes with c, d, and f; and f interferes only with e?

Graph Coloring Algorithm • Greedy Algorithm: 1. Label the vertices 2. Label the colors 3. Assign color 1 to vertex 1, if vertex 1 and 2 are adjacent use a different color or if not adjacent use 1 again 4. Continue to assign colors based on what vertices are adjacent to the other

The Four Color Problem • Is it true that the countries on any given map can be colored with four or fewer colors in such a way that adjacent countries are colored differently? • First studied in 1852 by Francis Guthrie but was not proved until 1976

Four Color Theorem • Every planar graph is 4 -colorable. • Every planar graph is 5 -colorable.

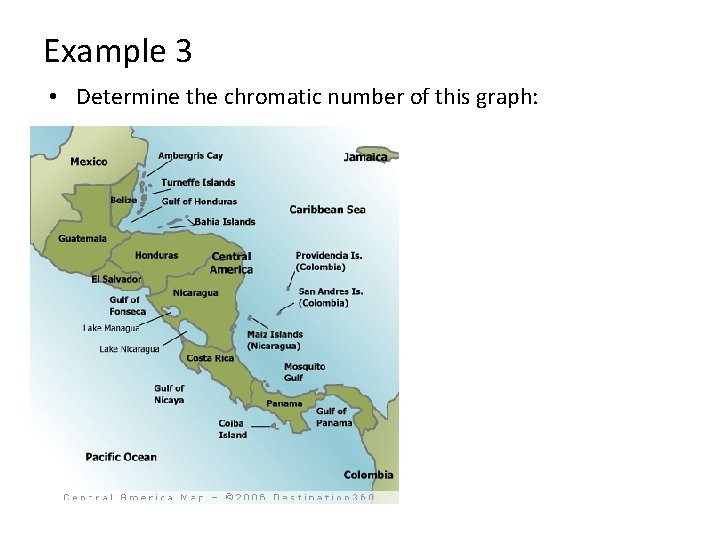
Example 3 • Determine the chromatic number of this graph: