Graph Theory Euler Circuits Christina Mende Math 480

Graph Theory: Euler Circuits Christina Mende Math 480 April 15, 2013

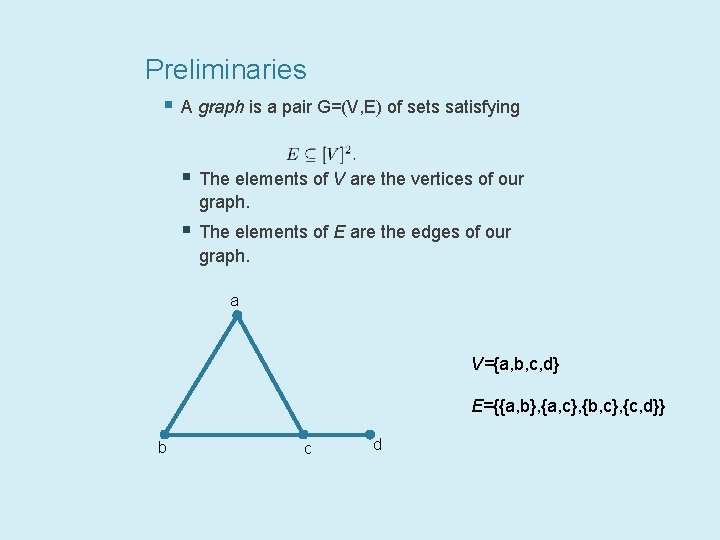
Preliminaries § A graph is a pair G=(V, E) of sets satisfying § The elements of V are the vertices of our graph. § The elements of E are the edges of our graph. a V={a, b, c, d} E={{a, b}, {a, c}, {b, c}, {c, d}} b c d

Preliminaries § The degree of a vertex v (denoted deg(v)) is the number of edges directly connected to that vertex. deg(a)=2 deg(b)=2 deg(c)=3 deg(d)=1 a V={a, b, c, d} E={{a, b}, {a, c}, {b, c}, {c, d}} b c d

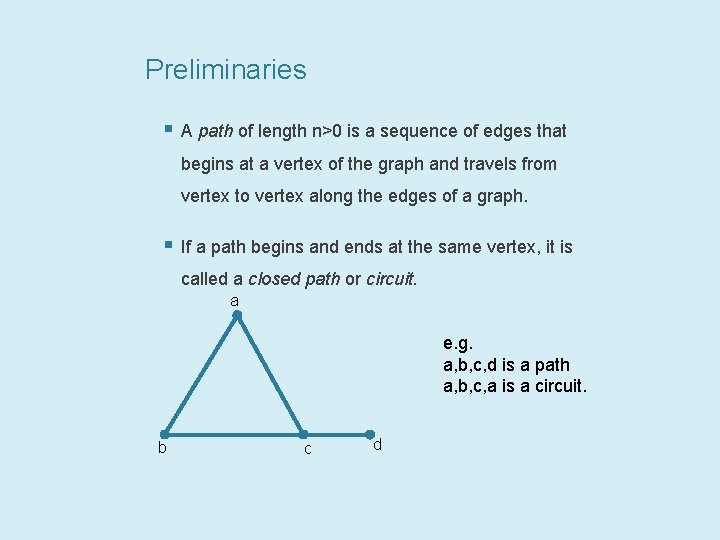
Preliminaries § A path of length n>0 is a sequence of edges that begins at a vertex of the graph and travels from vertex to vertex along the edges of a graph. § If a path begins and ends at the same vertex, it is called a closed path or circuit. a e. g. a, b, c, d is a path a, b, c, a is a circuit. b c d

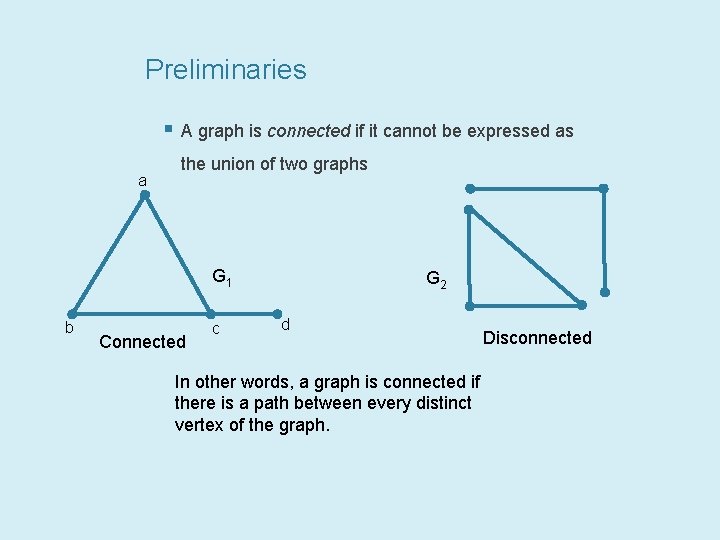
Preliminaries § A graph is connected if it cannot be expressed as a the union of two graphs G 1 b Connected c G 2 d In other words, a graph is connected if there is a path between every distinct vertex of the graph. Disconnected

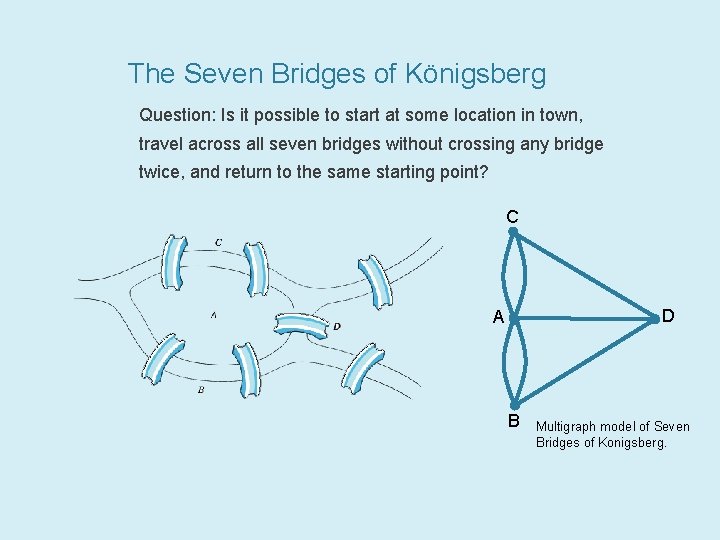
The Seven Bridges of Königsberg Question: Is it possible to start at some location in town, travel across all seven bridges without crossing any bridge twice, and return to the same starting point? C D A B Multigraph model of Seven Bridges of Konigsberg.

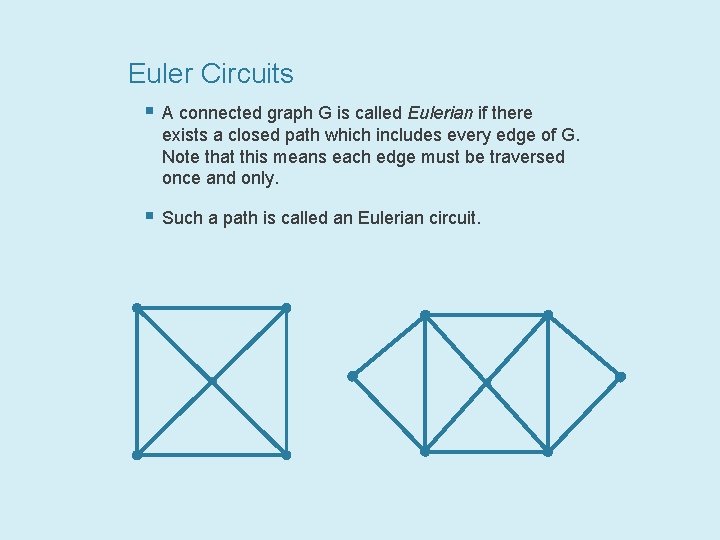
Euler Circuits § A connected graph G is called Eulerian if there exists a closed path which includes every edge of G. Note that this means each edge must be traversed once and only. § Such a path is called an Eulerian circuit.

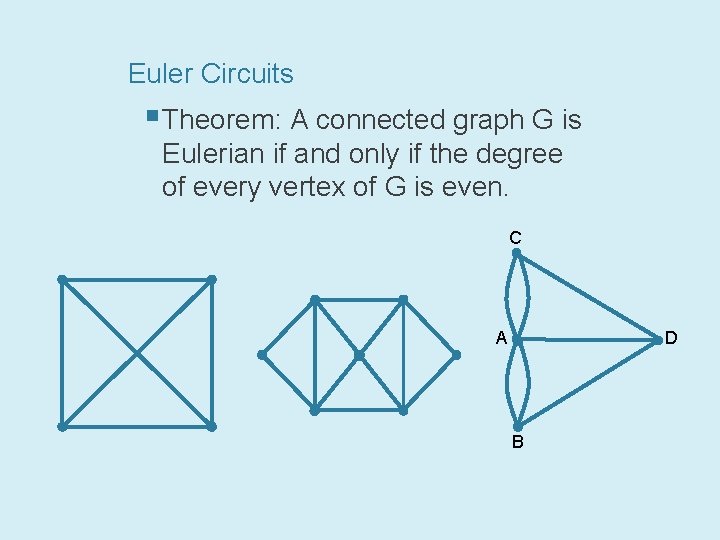
Euler Circuits § Theorem: A connected graph G is Eulerian if and only if the degree of every vertex of G is even. C D A B

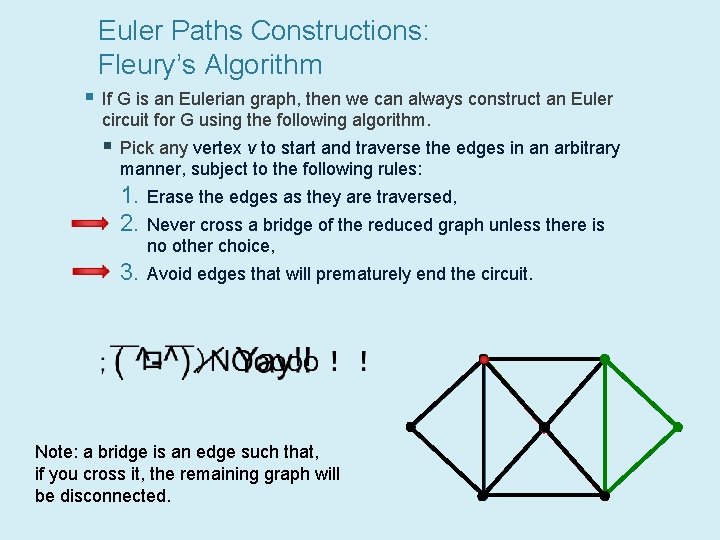
Euler Paths Constructions: Fleury’s Algorithm § If G is an Eulerian graph, then we can always construct an Euler circuit for G using the following algorithm. § Pick any vertex v to start and traverse the edges in an arbitrary manner, subject to the following rules: 1. Erase the edges as they are traversed, 2. Never cross a bridge of the reduced graph unless there is no other choice, 3. Avoid edges that will prematurely end the circuit. Note: a bridge is an edge such that, if you cross it, the remaining graph will be disconnected.

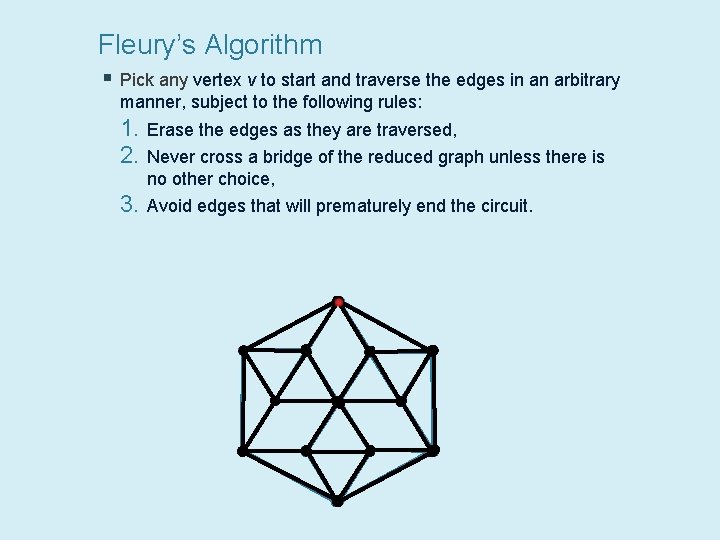
Fleury’s Algorithm § Pick any vertex v to start and traverse the edges in an arbitrary manner, subject to the following rules: 1. Erase the edges as they are traversed, 2. Never cross a bridge of the reduced graph unless there is no other choice, 3. Avoid edges that will prematurely end the circuit.

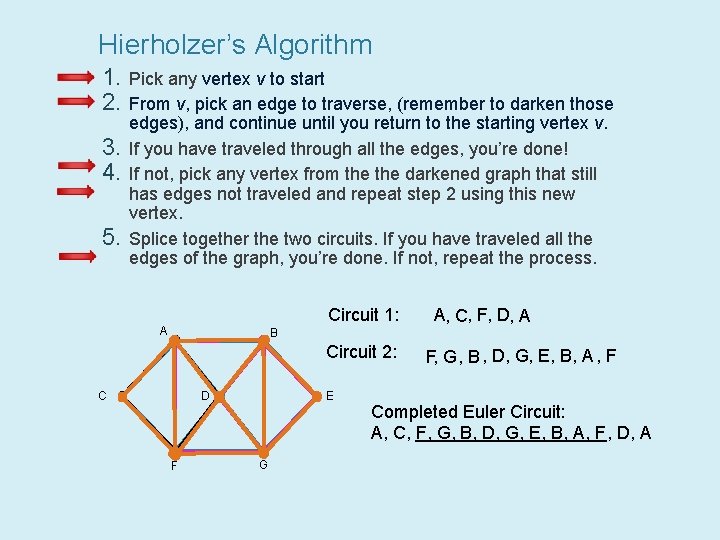
Hierholzer’s Algorithm 1. Pick any vertex v to start 2. From v, pick an edge to traverse, (remember to darken those 3. 4. 5. edges), and continue until you return to the starting vertex v. If you have traveled through all the edges, you’re done! If not, pick any vertex from the darkened graph that still has edges not traveled and repeat step 2 using this new vertex. Splice together the two circuits. If you have traveled all the edges of the graph, you’re done. If not, repeat the process. Circuit 1: A B Circuit 2: D C F E G A, C, F, D, A F, G, B , D, G, E, B, A, F Completed Euler Circuit: A, C, F, G, B, D, G, E, B, A, F, D, A

Any Questions? § References § R. Diestel, Graph Theory. § L. R. Foulds, Graph Theory Applications. § K. Rosen, Discrete Mathematics and Its Applications. § R. Wilson, Introduction To Graph Theory. Image from: http: //www. cs. sunysb. edu/~skiena/combinatorica/animations/euler. html