Graph Theory Chapter 7 Planar Graphs 2011 12

Graph Theory Chapter 7 Planar Graphs 大葉大學 資訊 程系 黃鈴玲 2011. 12

Contents Ø Ø Ø 7. 2 Planar Embeddings 7. 3 Euler’s Formula and Consequences 7. 4 Characterization of Planar Graphs 2

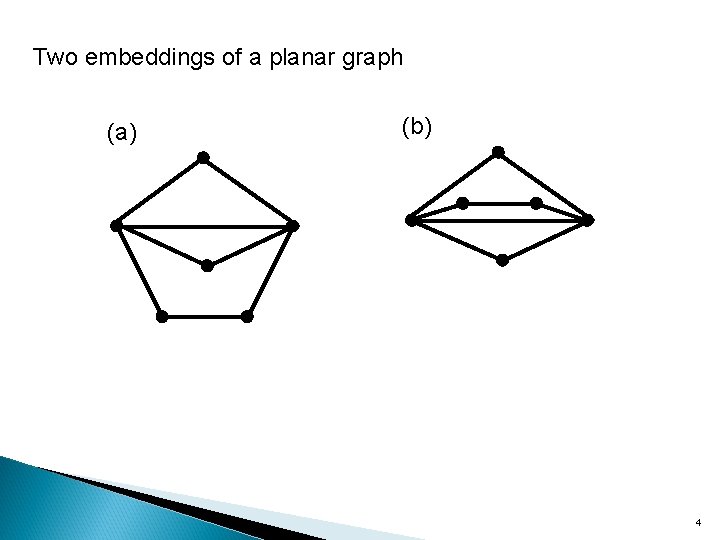
7. 2 Planar Embedding Definition A graph that can be drawn in the plane without any of its edges intersecting is called a planar graph. A graph that is so drawn in the plane is also said to be embedded (嵌入) in the plane. Applications: (1) circuit layout problems (2) Three house and three utilities(水電瓦斯) problem 3

Two embeddings of a planar graph (a) (b) 4

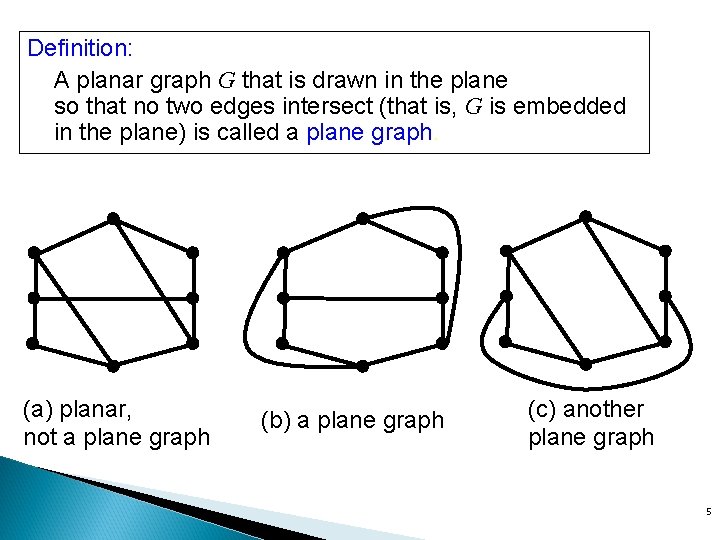
Definition: A planar graph G that is drawn in the plane so that no two edges intersect (that is, G is embedded in the plane) is called a plane graph. (a) planar, not a plane graph (b) a plane graph (c) another plane graph 5

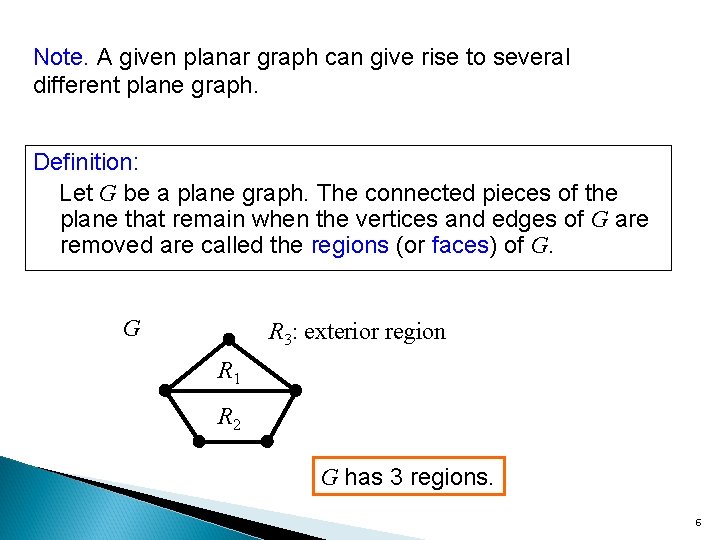
Note. A given planar graph can give rise to several different plane graph. Definition: Let G be a plane graph. The connected pieces of the plane that remain when the vertices and edges of G are removed are called the regions (or faces) of G. G R 3: exterior region R 1 R 2 G has 3 regions. 6

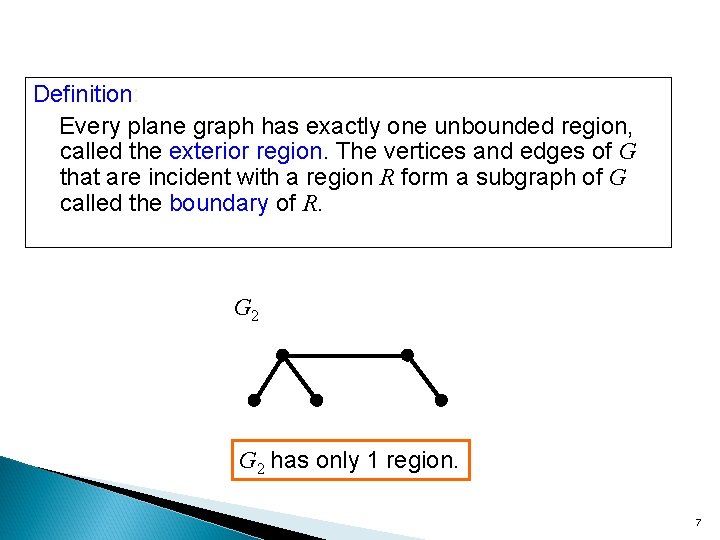
Definition: Every plane graph has exactly one unbounded region, called the exterior region. The vertices and edges of G that are incident with a region R form a subgraph of G called the boundary of R. G 2 has only 1 region. 7

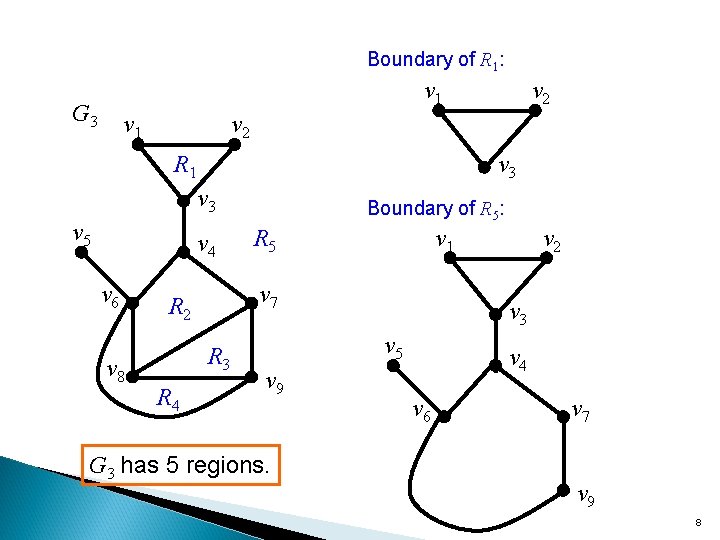
Boundary of R 1: v 1 G 3 v 1 v 2 v 3 R 1 v 3 v 5 v 4 v 6 v 8 v 2 v 1 R 5 v 7 R 2 R 3 R 4 Boundary of R 5: v 3 v 5 v 9 G 3 has 5 regions. v 2 v 4 v 6 v 7 v 9 8

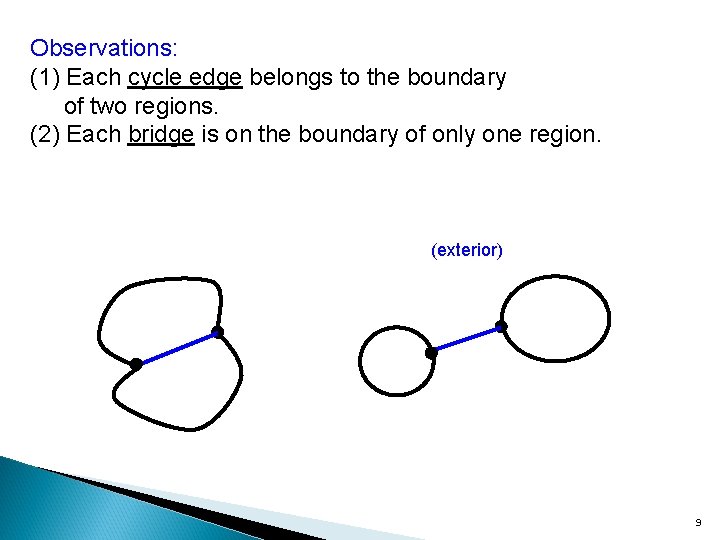
Observations: (1) Each cycle edge belongs to the boundary of two regions. (2) Each bridge is on the boundary of only one region. (exterior) 9

Homework Ex: Show that, for every positive integer n, the graph K 1, 1, n is planar. How many regions result when this graph is embedded in the plane? 10

7. 3 Euler’ Formula and Consequences Thm 7. 14 (Euler’s Formula) If G is a connected plane graph with p vertices, q edges, and r regions, then p - q + r = 2. pf: (by induction on q) (basis) If q = 0, then G K 1; so p = 1, r =1, and p - q + r = 2. (inductive) Assume the result is true for any graph with q = k - 1 edges, where k 1. 11

Let G be a graph with k edges. Suppose G has p vertices and r regions. If G is a tree, then G has p vertices, p-1 edges and 1 region. p - q + r = p – (p-1) + 1 = 2. If G is not a tree, then some edge e of G is on a cycle. Hence G-e is a connected plane graph having p vertices, k-1 edges, and r-1 regions. p - (k-1) + (r-1) = 2 (by assumption) p-k+r=2 # 12

Homework Ex: Let G be a 5 -regular planar graph with 20 vertices. How many regions result when this graph is embedded in the plane? 13

Definition: A plane graph G is called maximal planar if, for every pair u, v of nonadjacent vertices of G, the graph G+uv is nonplanar. Homework: Draw a maximal planar graph of 6 vertices. How many edges and regions are there in this graph? Thus, in any embedding of a maximal planar graph G of order at least 3, the boundary of every region of G is a triangle. 14

Theorem A: If G is a maximal planar graph with p 3 vertices and q edges, then q = 3 p - 6. pf Embed the graph G in the plane, resulting in r regions. p - q + r = 2. Since the boundary of every region of G is a triangle, every edge lies on the boundary of two regions. p - q + 2 q / 3 = 2. q = 3 p - 6 15

Corollary: If G is a maximal planar bipartite graph with p 3 vertices and q edges, then q = 2 p - 4. pf The boundary of every region is a 4 -cycle. 4 r = 2 q p - q + q / 2 = 2 q = 2 p - 4. Corollary: If G is a planar graph with p 3 vertices and q edges, then q 3 p - 6. pf: If G is not maximal planar, we can add edges to G to produce a maximal planar graph. By Theorem A 得證. 16

Corollary 7. 18: Every planar graph contains a vertex of degree 5 or less. pf Let G be a planar graph of p vertices and q edges. If deg(v) 6 for every v V(G) 2 q 6 p 17

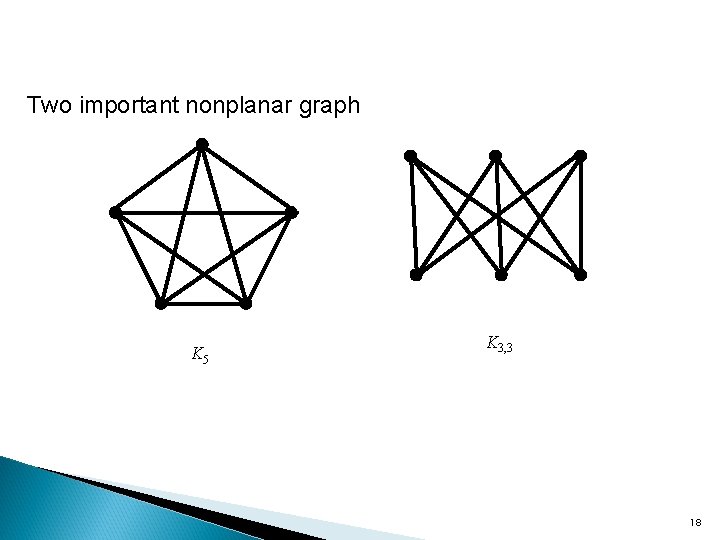
Two important nonplanar graph K 5 K 3, 3 18

Observation 7. 17 The graphs K 5 and K 3, 3 are nonplanar. pf (1) K 5 has p = 5 vertices and q = 10 edges. q > 3 p - 6 K 5 is nonplanar. (2) Suppose K 3, 3 is planar, and consider any embedding of K 3, 3 in the plane. Suppose the embedding has r regions. p-q+r=2 r=5 K 3, 3 is bipartite The boundary of every region has 4 edges. 19

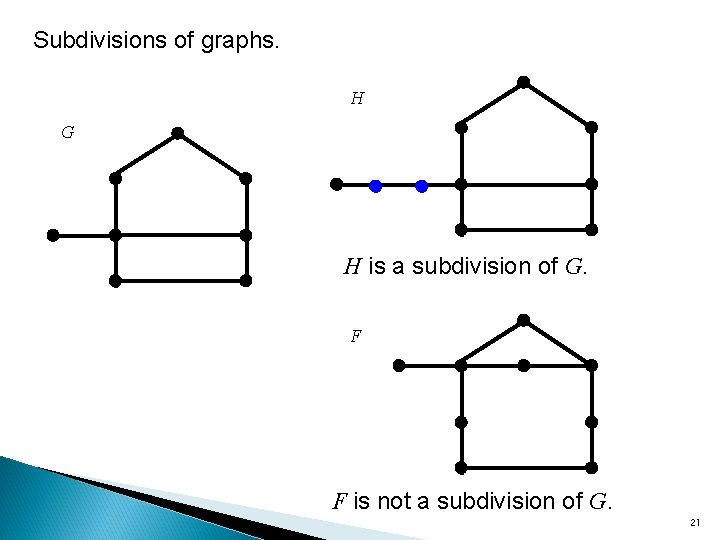
7. 4 Characterization of Planar Graphs Definition 7. 20 Let G be a graph and e={u, v} an edge of G. A subdivision of e is the replacement of the edge e by a simple path (u 0, u 1, …, uk), where u 0 = u and uk =v are the only vertices of the path in V(G). of G. We say that G’ is a subdivision of G if G’ is obtained from G by a sequence of subdivisions of edges in G. 把edge e用 一條path取代 20

Subdivisions of graphs. H G H is a subdivision of G. F F is not a subdivision of G. 21

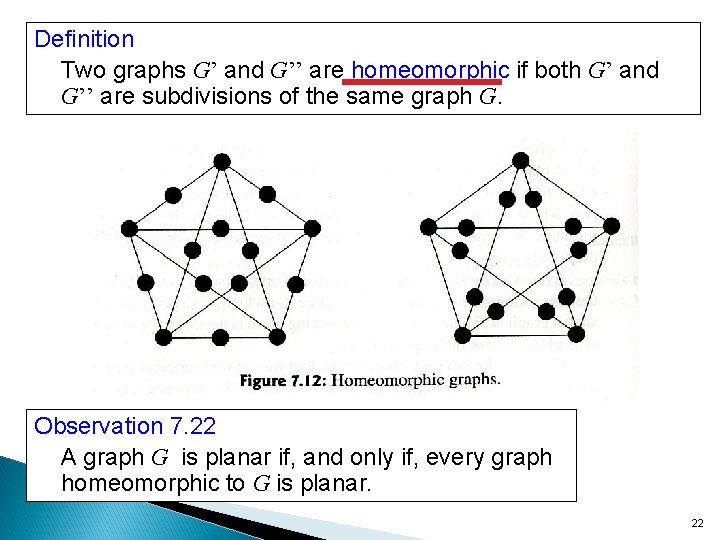
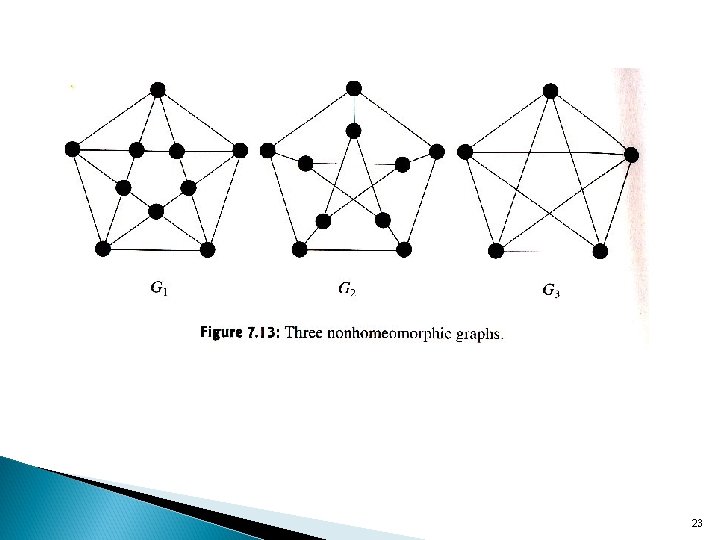
Definition Two graphs G’ and G’’ are homeomorphic if both G’ and G’’ are subdivisions of the same graph G. Observation 7. 22 A graph G is planar if, and only if, every graph homeomorphic to G is planar. 22

23

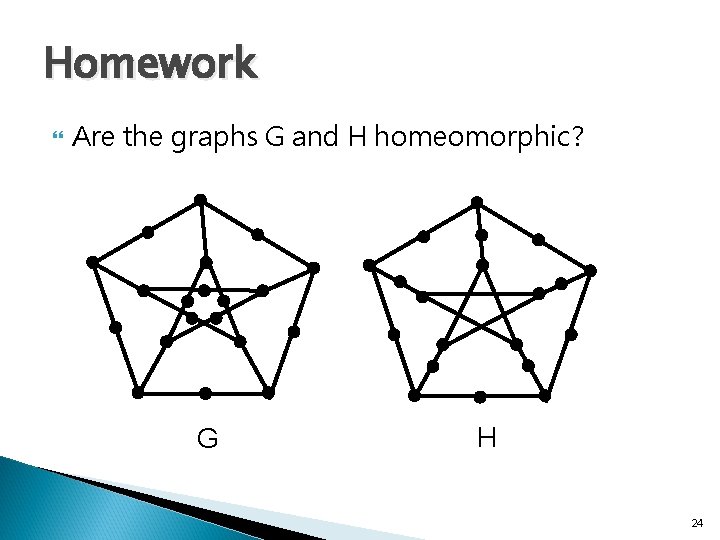
Homework Are the graphs G and H homeomorphic? G H 24

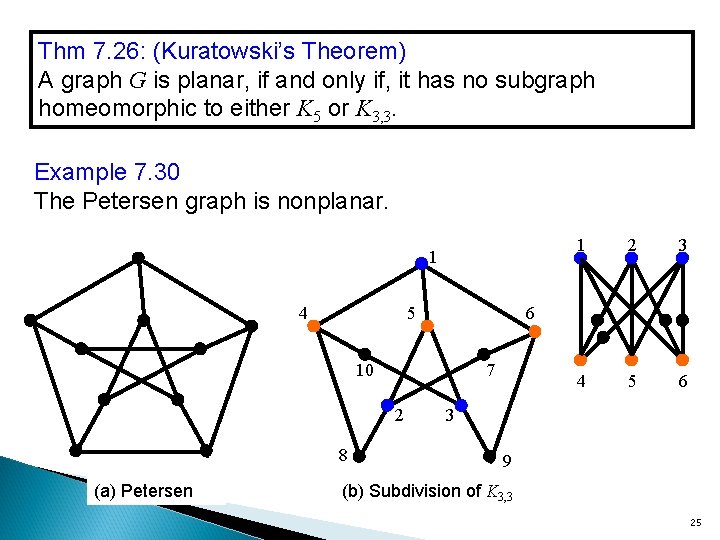
Thm 7. 26: (Kuratowski’s Theorem) A graph G is planar, if and only if, it has no subgraph homeomorphic to either K 5 or K 3, 3. Example 7. 30 The Petersen graph is nonplanar. 1 4 5 8 (a) Petersen 2 3 4 5 6 6 10 7 2 1 3 9 (b) Subdivision of K 3, 3 25

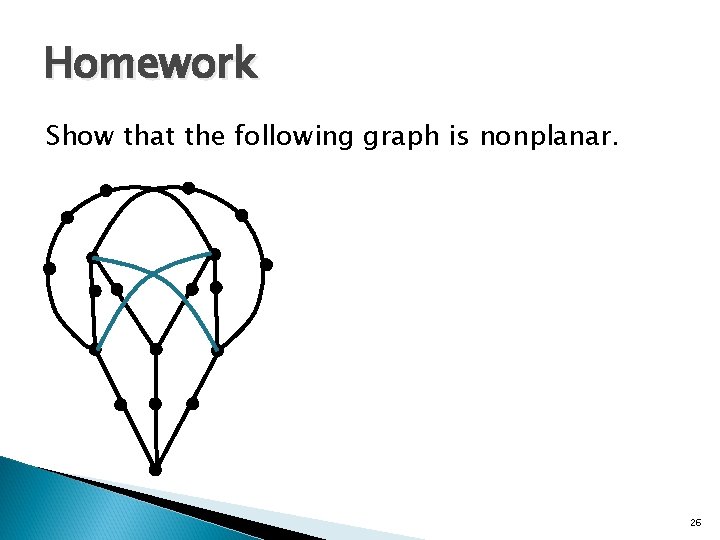
Homework Show that the following graph is nonplanar. 26