Graph Theory Chapter 4 Connectivity and Paths Ch

Graph Theory Chapter 4 Connectivity and Paths Ch. 4. Connectivity and paths 1

Graph Theory Connectivity 4. 1. 1 q A separating set or vertex cut of a graph G is a set S⊆V(G) such that G-S has more than one component q The connectivity of G, written (G), is the minimum size of a vertex set S such that G-S is disconnected or has only one vertex q A graph G is k-connected if its connectivity is at least k. Ch. 4. Connectivity and paths 2

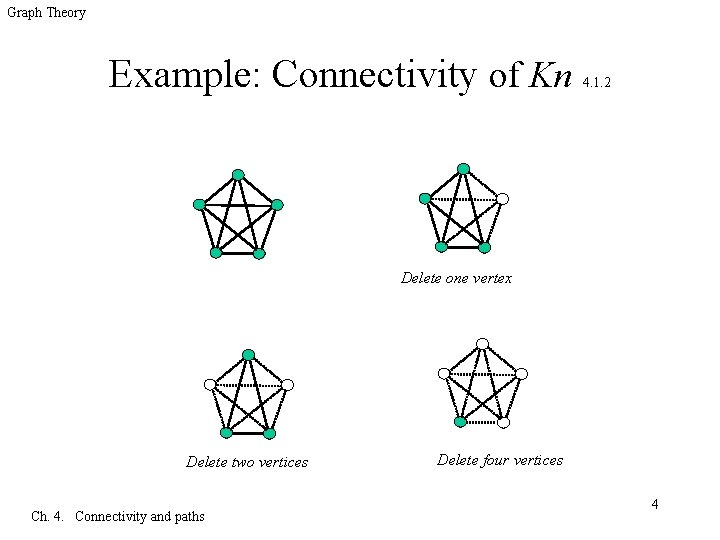
Graph Theory Example: Connectivity of Kn 4. 1. 2 q Because a clique has no separating set, we need to adopt a convention for its connectivity. – This explains the phrase “or has only one vertex” in Definition 4. 1. 1. q We obtain (Kn)=n-1, while (G)≤n(G)-2 when G is not a complete graph – With this convention, most general results about connectivity remain valid on complete graphs Ch. 4. Connectivity and paths 3

Graph Theory Example: Connectivity of Kn 4. 1. 2 Delete one vertex Delete two vertices Ch. 4. Connectivity and paths Delete four vertices 4

Graph Theory Example: Connectivity of Km, n 4. 1. 2 q Consider a bipartition X, Y of Km, n. – Every induced subgraph that has at least one vertex from X and from Y is connected. – Hence every separating set of Km, n contains X or Y. – Since X and Y themselves are separating sets (or leave only one vertex), we have (Km, n) = min{m, n}. q The connectivity of K 3, 3 is 3; the graph is 1 connected, 2 -connected, and 3 -connected, but not 4 -connected. 5 Ch. 4. Connectivity and paths

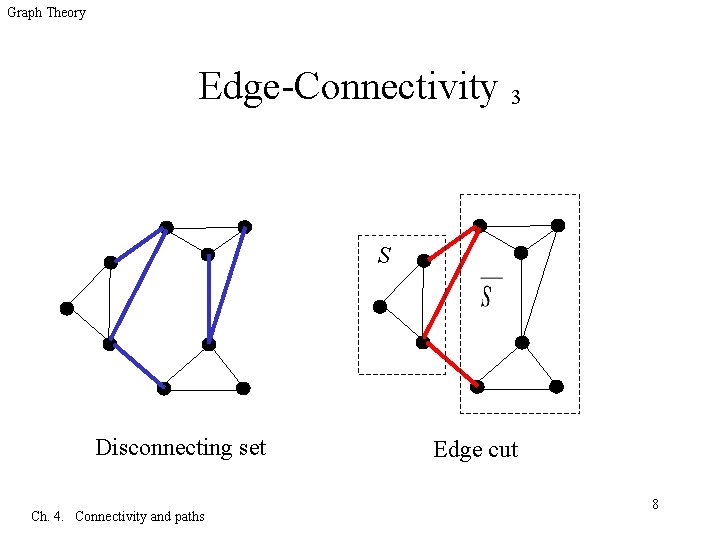
Graph Theory Edge-Connectivity 1 4. 1. 7 q A disconnecting set of edges is a set F⊆E(G) such that G-F has more than one component. (also called a cut) – A graph is k-edge-connected if every disconnecting set has at least k edges. – The edge-connectivity of G, written ’(G), is the minimum size of a disconnecting set. Ch. 4. Connectivity and paths 6

Graph Theory Edge-Connectivity 2 4. 1. 7 q Given S, T⊆V(G), we write [S, T] for the set of edges having one end-point in S and the other in T. q An edge cut is an edge set of the form [S, Ŝ], where S is a nonempty proper subset of V(G) and Ŝ denotes V(G)-S. (also called a cut-set) Ch. 4. Connectivity and paths 7

Graph Theory Edge-Connectivity 3 S Disconnecting set Ch. 4. Connectivity and paths Edge cut 8

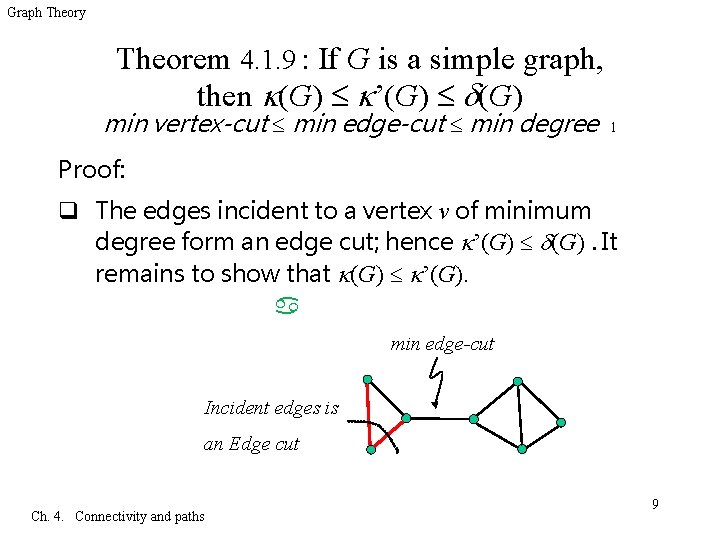
Graph Theory Theorem 4. 1. 9 : If G is a simple graph, then (G) ’(G) min vertex-cut min edge-cut min degree 1 Proof: q The edges incident to a vertex v of minimum degree form an edge cut; hence ’(G) (G). It remains to show that (G) ’(G). min edge-cut Incident edges is an Edge cut Ch. 4. Connectivity and paths 9

Graph Theory Theorem 4. 1. 9 : If G is a simple graph, then (G) ’(G) vertex-cut edge-cut minimum degree 1 Proof: continue q We have observed that (G) n(G)-1 (see Example 4. 1. 2). Consider a smallest edge cut [S, S ]. q If every vertex of S is adjacent to every vertex of S, then |[S, S ]| = |S |≥n(G)-1≥ (G), and the desired inequality holds. Ch. 4. Connectivity and paths 10

Graph Theory Theorem 4. 1. 9 2 Proof: Continue q Otherwise, we choose x S and y S with x y. q Let T consist of all neighbors of x in S and all vertices of S -{x} with neighbors in S. q Every x, y-path passes through T, so T is a separating set. q Also, picking the edges from x to T S and one edge from each vertex of T S to S (shown bold below) yields |T| distinct edges of [S, S ]. q Thus ’(G)= |[ S, S ]|≥ |T| ≥ (G). x neighbors of x : 1, 2 T: {1, 2, b, c, d} Ch. 4. Connectivity and paths S a b c d 1 2 3 S 4 11

Graph Theory Bond 4. 1. 14 q A bond is a minimal nonempty edge cut. q Here “minimal” means that no proper nonempty subset is also an edge cut. – We characterize bonds in connected graphs. Ch. 4. Connectivity and paths 12

Graph Theory Proposition 4. 1. 15: If G is a connected graph, then an edge cut F is a bond if and only if G-F has exactly two components 1 Proof: q Let F = [S, S] be an edge cut. q Suppose that G-F has exactly two components, and let F’ F. q The graph G-F’ contains the two components of G-F plus at least one edge between them, making it connected. q Hence F is a minimal disconnecting set and is bond. Ch. 4. Connectivity and paths 13

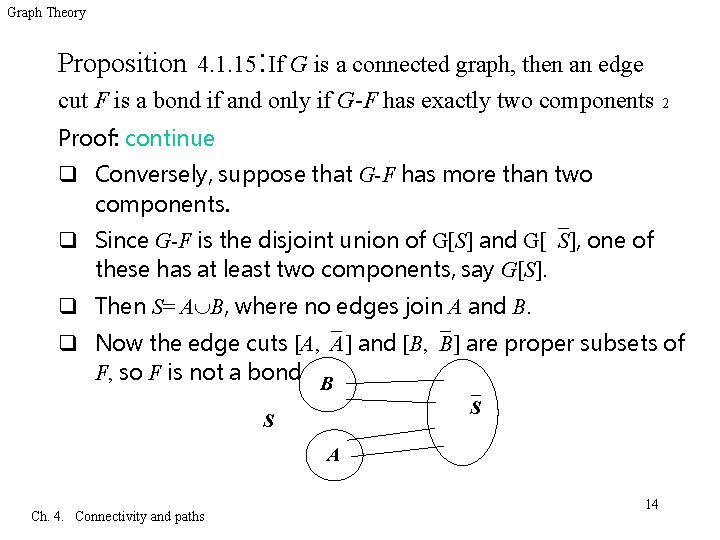
Graph Theory Proposition 4. 1. 15: If G is a connected graph, then an edge cut F is a bond if and only if G-F has exactly two components 2 Proof: continue q Conversely, suppose that G-F has more than two components. q Since G-F is the disjoint union of G[S] and G[ S], one of these has at least two components, say G[S]. q Then S= A B, where no edges join A and B. q Now the edge cuts [A, A] and [B, B] are proper subsets of F, so F is not a bond B S S A Ch. 4. Connectivity and paths 14

Graph Theory Blocks q A block of a graph G is a maximal connected subgraph of G that has no cut-vertex. – If G itself is connected and has no cut-vertex, then G is a block. Ch. 4. Connectivity and paths 15

Graph Theory Example of Blocks 4. 1. 17 q If H is a block of G, then H as a graph has no cutvertex, but H may contain vertices that are cutvertices of G. – For example, the graph drawn below has five blocks; three copies of K 2, one of K 3, and one subgraph that is neither a cycle nor a complete graph. Ch. 4. Connectivity and paths

Graph Theory Proposition 4. 1. 19: Two blocks in a graph share at most one vertex. Proof: q Use contradiction. – Suppose that blocks B 1, B 2 have at least two common vertices. – We show that B 1∪B 2 is a connected subgraph with no cut-vertex, which contradicts the maximality of B 1 and B 2. Ch. 4. Connectivity and paths 17

Graph Theory Proposition 4. 1. 19: Two blocks in a graph share at most one vertex. Proof: Continue q When delete one vertex v from Bi, what remains is connected. q Hence any path in Bi from every vertex in Bi-{v} to any in V(B 1)∩V(B 2)-{v} is retained. q Since the blocks have at least two common vertices, deleting a single vertex leaves a vertex in the intersection. q Paths from all vertices to that vertex are retained, so B 1∪B 2 cannot be disconnected by deleting one vertex. Ch. 4. Connectivity and paths 18

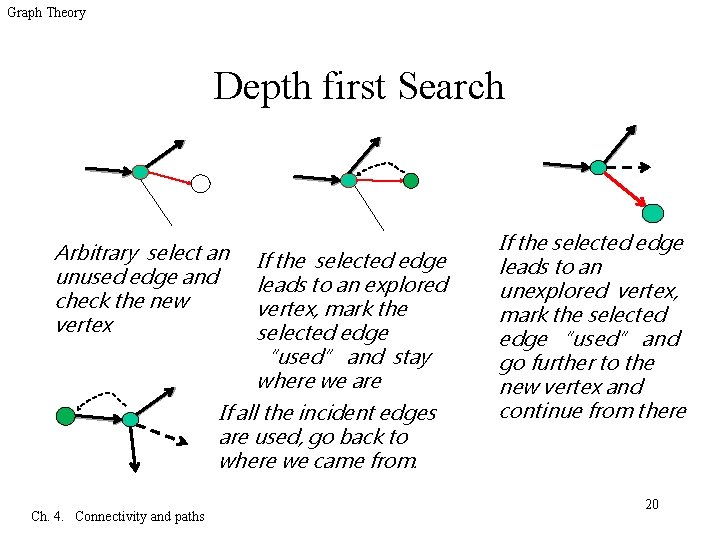
Graph Theory Depth First Search q Depth first search: Explore always from the most recently discovered vertex that has unexplored edges. – Use stack q Breadth first search: Explores from the oldest vertex. – Use queue Ch. 4. Connectivity and paths 19

Graph Theory Depth first Search Arbitrary select an unused edge and check the new vertex If the selected edge leads to an explored vertex, mark the selected edge “used” and stay where we are If all the incident edges are used, go back to where we came from. Ch. 4. Connectivity and paths If the selected edge leads to an unexplored vertex, mark the selected edge “used” and go further to the new vertex and continue from there 20

Graph Theory Example of Depth First Search 4. 1. 21 q Depth-first search from u – u, a, b, c, d, e, f, g g f e d u a b c Ch. 4. Connectivity and paths 1. From u go to a, b, c, d 2. From d, try to get to b but b is visited 3. From d, no other unvisited edge to go, so go back to c 4. Similarly, no other unvisited edge to go from c , go back to b 5. From b go to e 6. No other unvisited edge to go from e, go back to b and then a 7. From a, go to f and then g 8. From g go to u but u is visited 9. From g go back to f, a, and then 21 u

Graph Theory Example of Depth First Search 4. 1. 21 q Other Depth-first search paths from u – u, a, f, g, b, e, d, c – u, g, f, a, b, c, d, e g f e d u a b c Ch. 4. Connectivity and paths 22

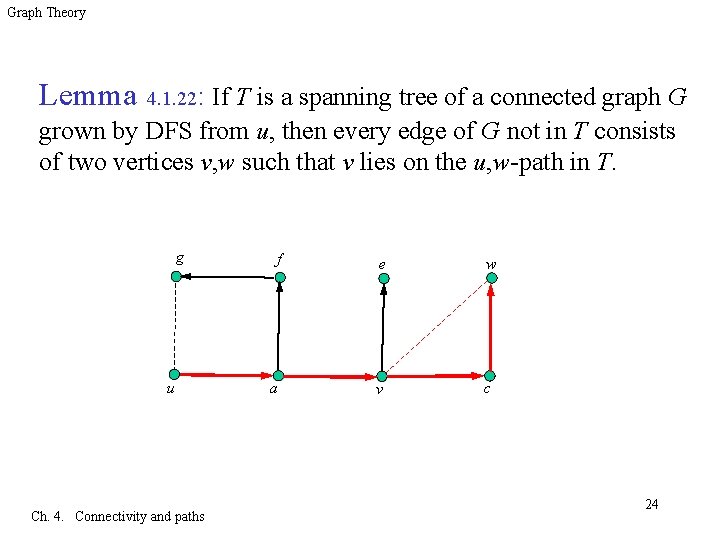
Graph Theory Lemma 4. 1. 22: If T is a spanning tree of a connected graph G grown by DFS from u, then every edge of G not in T consists of two vertices v, w such that v lies on the u, w-path in T. Proof: q Let v w be an edge of G, with v encountered before w in the depth-first search. q Because v w is an edge, we cannot finish v before w is added to T. q Hence w appears somewhere in the subtree formed before finishing v, and the path from w to u contains v. q See example in the next page Ch. 4. Connectivity and paths 23

Graph Theory Lemma 4. 1. 22: If T is a spanning tree of a connected graph G grown by DFS from u, then every edge of G not in T consists of two vertices v, w such that v lies on the u, w-path in T. g u Ch. 4. Connectivity and paths f e w a v c 24

Graph Theory Algorithm: 4. 1. 23 Computing the blocks of a graph 1/2 q Input: A connected graph G. q Idea: Build a depth-first search tree T of G, discarding portions of T as blocks are identified. Maintain one vertex called ACTIVE. q Initialization: Pick a root x∈ V(H); make x ACTIVE; set T={x}. Ch. 4. Connectivity and paths 25

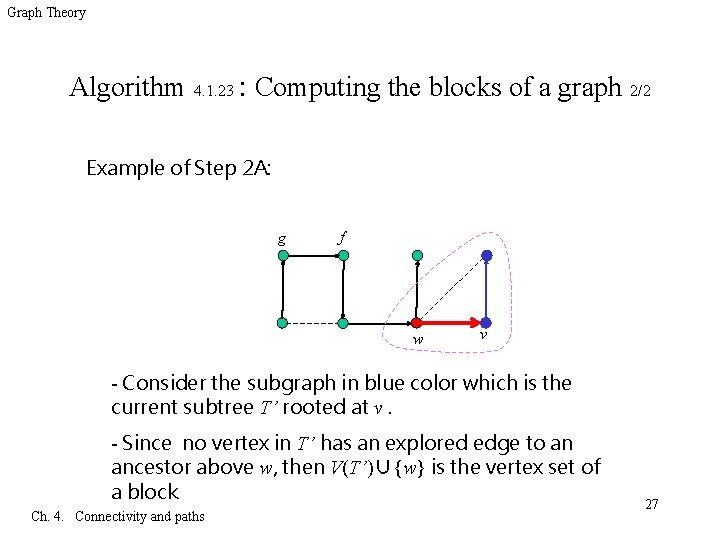
Graph Theory Algorithm 4. 1. 23 : Computing the blocks of a graph 2/2 q Iteration: Let v denote the current active vertex. 1) If v has an unexplored incident edge vw, then 1 A) If w V(T), then add vw to T, mark vw explored, make w ACTIVE. 1 B) If w∈ V(T), then w is an ancestor of v; mark vw explored. 2) If v has no more unexplored incident edges, then 2 A) If v ≠ x, and w is the parent of v, make w ACTIVE. If no vertex in the current subtree T’ rooted at v has an explored edge to an ancestor above w, then V(T’)∪{w} is the vertex set of a block; record this information and delete V(T’) from T. ( see example in the next page) 2 B) If v = x, terminate. Ch. 4. Connectivity and paths 26

Graph Theory Algorithm 4. 1. 23 : Computing the blocks of a graph 2/2 Example of Step 2 A: g f w v - Consider the subgraph in blue color which is the current subtree T’ rooted at v. - Since no vertex in T’ has an explored edge to an ancestor above w, then V(T’)∪{w} is the vertex set of a block Ch. 4. Connectivity and paths 27

Graph Theory Theorem 4. 2. 2 : A graph G having at least three vertices is 2 -connected if and only if for each pair u, v∈ V(G) there exist internally disjoint u, v-paths in G. (Whitney [1932 a]) q Sufficiency: – When G has internally disjoint u, v-paths, deletion of one vertex cannot separate u from v. – Since this condition is given for every pair u, v, deletion of one vertex cannot make any vertex unreachable from any other. – We conclude that G is 2 -connected. q Necessity: by induction method Ch. 4. Connectivity and paths 28

Graph Theory Lemma: (Expansion Lemma) If G is a k-connected graph, and G’ is obtained from G by adding a new vertex y with at least k neighbors in G, then G’ is k-connected. 4. 2. 3 Proof: We prove that a separating set S of G’ must have size at least k. – If y S, then S-{y} separates G, so |S| k+1. – If y S and N(y) S, then |S | k. – Otherwise, y and N(y)-S lie in a single component of G’-S. – Thus again S must separate G and |S| k. Ch. 4. Connectivity and paths 29

Graph Theory Theorem 4. 2. 4. For a graph G with at least three vertices, the following conditions are equivalent. A) G is connected and has no cut-vertex. B) For all x, y V(G), there are internally disjoint x, ypaths C) For all x, y V(G), there is a cycle through x and y. D) (G) 1, and every pair of edges in G lies on a common cycle. Ch. 4. Connectivity and paths 30

Graph Theory Corollary 4. 2. 6 : If G is 2 -connected, then the graph G’ obtained by subdividing an edge of G is 2 -connected. Proof: q Let G’ be formed from G by adding vertex w to subdivide uv. To show that G’ is 2 -connected, it suffice to find a cycle through arbitrary edges e, f of G’(by Theorem 4. 2. 4 D). q Since G is 2 -connected, any two edges of G lie on a common cycle (Theorem 4. 2. 4 D). q When our given edges e, f of G’ lie in G, a cycle through them in G is also in G’, unless it uses uv, in which case we modify the cycle. Here “modify the cycle” means “replace the edge uv with the u, v-path of length 2 through w”. q When e ∈ E(G) and f ∈ {uw, wv}, we modify a cycle passing through e and uv in G. When {e, f}={uw, wv}, we 31 Ch. 4. Connectivity and paths modify a cycle through uv.

Graph Theory Network Flow Problems 4. 3 q A network is : – A digraph with a nonegative capacity c(e) on each edge e and – A distinguished source vertex s and sink vertex t. – Vertices are also called node s. Ch. 4. Connectivity and paths 32

Graph Theory Network Flow Problems 4. 3 q A flow f assigns a value f(e) to each edge e. q Let: – f+(v) : the total flow on edges leaving v and – f –(v): the total flow on edges entering v q A flow is feasible if it satisfies – The capacity constraints 0≤f(e)≤c(e) for each edge and – The conservation constraints f+ (v) = f – (v) for each node v {s, t}. Ch. 4. Connectivity and paths 33

Graph Theory Maximum Network Flow q The value val(f) of a flow f is the net flow f –(t)-f +(t) into the sink. q A maximum flow is a feasible flow of maximum value. Ch. 4. Connectivity and paths 34

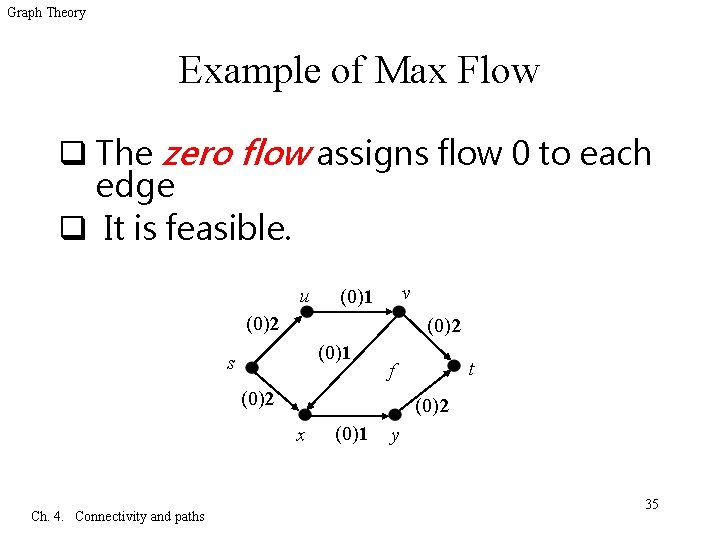
Graph Theory Example of Max Flow q The zero flow assigns flow 0 to each edge q It is feasible. u v (0)1 (0)2 (0)1 s (0)2 x Ch. 4. Connectivity and paths t f (0)1 y 35

Graph Theory Example of Max Flow q In the network below we illustrate a nonzero feasible flow. – Capacities are shown in bold, flow values in parentheses. – Our flow f assigns f(sx) = f(vt) = 0, and f(e) = 1 for every other edge e. This is a feasible flow of value 1. u v (1)1 (1)2 (0)2 (1)1 s (0)2 (1)2 x Ch. 4. Connectivity and paths t f (1)1 y 36

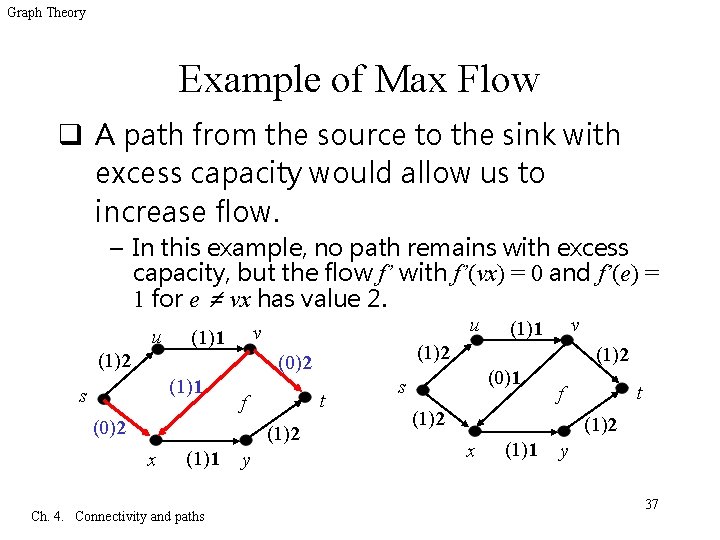
Graph Theory Example of Max Flow q A path from the source to the sink with excess capacity would allow us to increase flow. – In this example, no path remains with excess capacity, but the flow f’ with f’(vx) = 0 and f’(e) = 1 for e ≠ vx has value 2. u u v (1)1 (1)2 (0)2 (1)1 s t f (0)2 (1)2 x (1)1 Ch. 4. Connectivity and paths y v (1)1 (1)2 (0)1 s t f (1)2 x (1)1 y 37

Graph Theory f-Augmenting Path 4. 3. 4 q When f is a feasible flow in a network N, an faugmenting path is a source-to-sink path P in the underlying graph G such that for each e ∈ E(P), a) if P follows e in the forward direction, then f(e) < c(e). b) if P follows e in the backward direction, then f(e)>0. q Let ε(e)=c(e) - f(e) when e is forward on P, and let ε(e)=f(e) when e is backward on P. The tolerance 38 Ch. 4. Connectivity and min paths e∈ E(P)ε(e). of P is

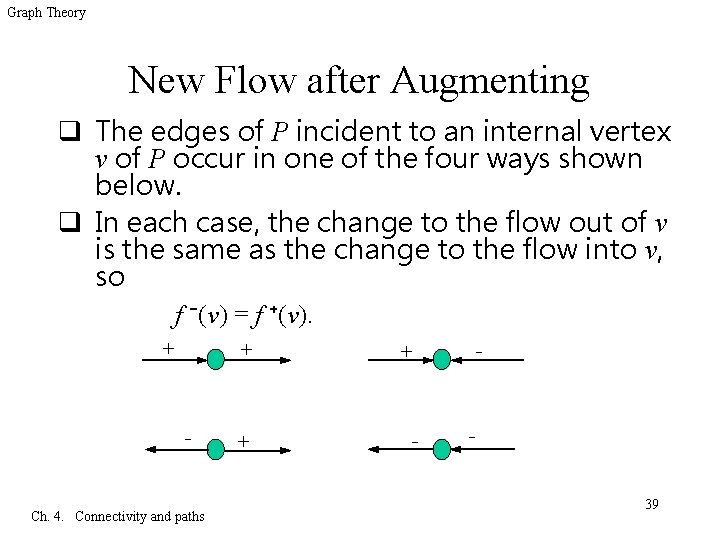
Graph Theory New Flow after Augmenting q The edges of P incident to an internal vertex v of P occur in one of the four ways shown below. q In each case, the change to the flow out of v is the same as the change to the flow into v, so f ⁻(v) = f ⁺(v). + - Ch. 4. Connectivity and paths + + + - - - 39

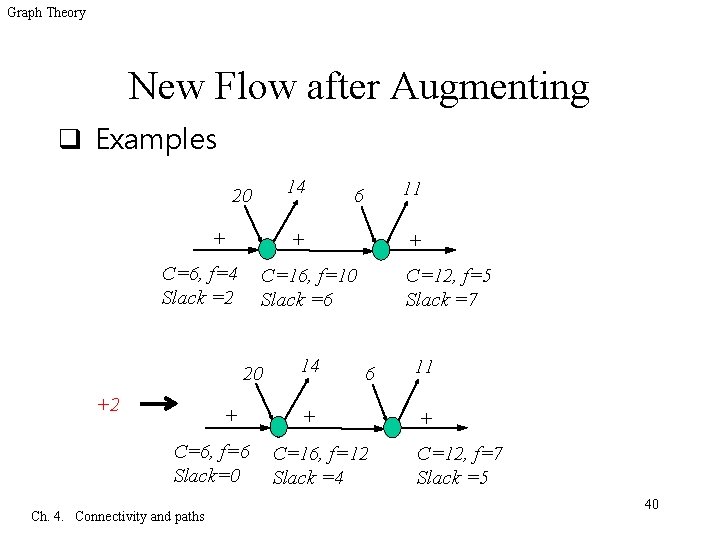
Graph Theory New Flow after Augmenting q Examples 14 20 + + C=6, f=4 Slack =2 + C=6, f=6 Slack=0 Ch. 4. Connectivity and paths + C=16, f=10 Slack =6 20 +2 11 6 14 C=12, f=5 Slack =7 6 + C=16, f=12 Slack =4 11 + C=12, f=7 Slack =5 40

Graph Theory New Flow after Augmenting q Examples +k Ch. 4. Connectivity and paths +k -k -k +k 41

Graph Theory New Flow after Augmenting q Examples 3/8 S=5 f/c= 6/9 S=3 12 15 Σin = 6+12 , Σout = 3+15 6/9 S=6 9 6 6 4 3/9 6/8 f/c= 9/9 4/11 S=4 4/11 S=7 17 1/11 9 7/11 3 more 12 15 Ch. 4. Connectivity and paths 9 6 6 4 17 9 42

Graph Theory Lemma. If P is an f-augmenting path with tolerance z, then changing flow by +z on edges followed forward by P and by –z on edges followed backward by P produces a feasible flow f’ with val(f’) = val(f)+z. Proof: q The definition of tolerance ensures that 0 ≤ f’(e) ≤ c(e) for every edge e, so the capacity constraints hold. – We need only check vertices of P, since flow elsewhere has not changed. q For every vertex v, f+(v) = f–(v) q Finally, the net flow into the sink t increases by z. + Ch. 4. Connectivity and paths - + + - - + 43

Graph Theory Source/sink cut q In a network, a source/sink cut [S, T] consists of the edges from a source set S to a sink set T, where S and T partition the set of nodes, with s ∈ S and t ∈ T. q The capacity of the cut [S, T], written cap(S, T), is the total of the capacities on the edges of [S, T]. q Keep in mind that in a digraph [S, T] denotes the set of edges with tail in S and head in T. Thus the capacity of a cut [S, T] is completely 44 Ch. 4. Connectivity and paths unaffected by edges from T to S.

Graph Theory Ford-Fulkerson Labeling Alg. For Max- flow 1 4. 3. 9 q Input: A feasible flow f in a network. q Output: An f-augmenting path or a cut with capacity val(f). q Idea: Find the nodes reachable from s by paths with positive tolerance. Reaching t completes an f-augmenting path. During the search, R is the set of nodes labeled Reached, and S is the subset of R labeled Searched. Ch. 4. Connectivity and paths 45

Graph Theory Ford-Fulkerson Labeling Alg. For Max- flow 2 Initialization: R = {s}, S = . Iteration: Choose v ∈ R-S. q For each exiting edge vw with f(vw) < c(vw) and w ∉ R, add w to R. q For each entering edge uv with f(uv>0) and u ∉ R, add u to R. q Label each vertex added to R as “reached”, and record v as the vertex reaching it. After exploring all edges at v, add v to S. q If the sink t has been reached (put in R), then trace the path reaching t to report an f-augmenting path and terminate. If R = S, then return the cut [S, Ŝ] and terminate. 46 Ch. 4. Connectivity and paths Otherwise, iterate.

Graph Theory Theorem 4. 3. 11 q In every network, The maximum flow = The minimum source/sink cut Ch. 4. Connectivity and paths 47

Graph Theory Max Flow and Bipartite Matching C=1 S Ch. 4. Connectivity and paths C=1 T 48