Graph Theory Chapter 3 Matchings and Factors Matchings

Graph Theory Chapter 3 Matchings and Factors Matchings and Covers Algorithms and Applications Matchings in General Graph Ch. 3. Matchings and Factors 1

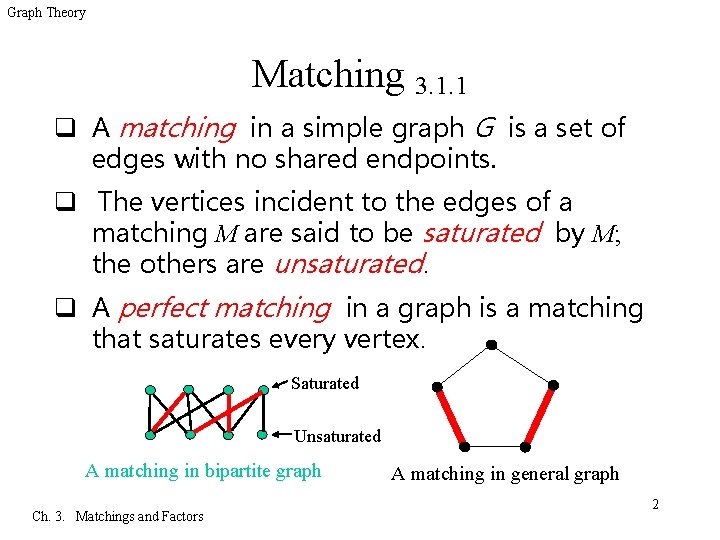
Graph Theory Matching 3. 1. 1 q A matching in a simple graph G is a set of edges with no shared endpoints. q The vertices incident to the edges of a matching M are said to be saturated by M; the others are unsaturated. q A perfect matching in a graph is a matching that saturates every vertex. Saturated Unsaturated A matching in bipartite graph Ch. 3. Matchings and Factors A matching in general graph 2

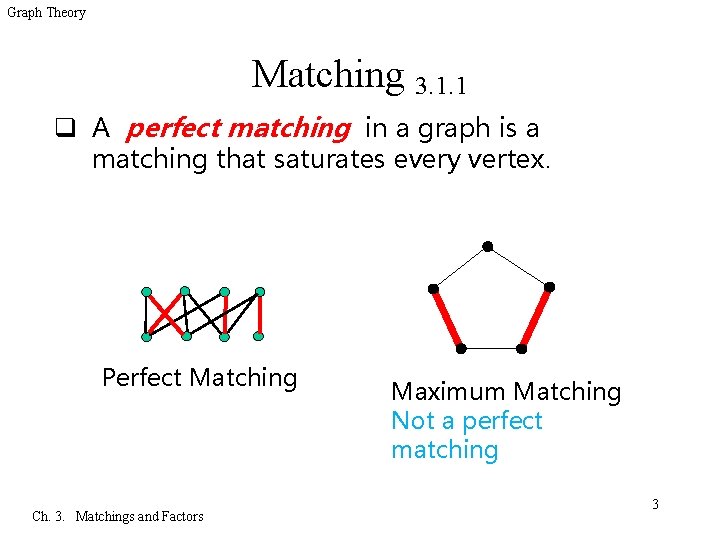
Graph Theory Matching 3. 1. 1 q A perfect matching in a graph is a matching that saturates every vertex. Perfect Matching Ch. 3. Matchings and Factors Maximum Matching Not a perfect matching 3

Graph Theory Example: Perfect matching in Kn, n 3. 1. 2 q Consider Kn, n with partite sets X={x 1, …, xn} and Y={y 1, …, yn}. q A perfect matching defines a bijection from X to Y. q Successively finding mates for x 1, x 2, … yields n! perfect matchings. – Each matching is represented by a permutation of [n], mapping i to j when xi is matched to yj. Ch. 3. Matchings and Factors 4

Graph Theory Example: Perfect matching in Kn, n 3. 1. 2 q For K 3, 3, there are: 123, 132, 213, 231, 312, 321. – 312: (x 1 -y 3) (x 2 -y 1) (x 3 -y 2) Ch. 3. Matchings and Factors 5

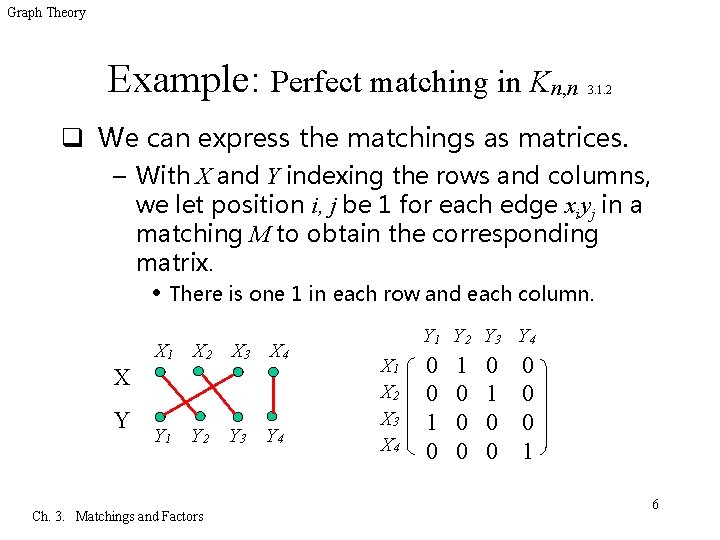
Graph Theory Example: Perfect matching in Kn, n 3. 1. 2 q We can express the matchings as matrices. – With X and Y indexing the rows and columns, we let position i, j be 1 for each edge xiyj in a matching M to obtain the corresponding matrix. • There is one 1 in each row and each column. X 1 X 2 X 3 X 4 X Y Y 1 Y 2 Y 3 Y 4 Ch. 3. Matchings and Factors Y 1 Y 2 Y 3 Y 4 X 1 X 2 X 3 X 4 0 0 1 0 0 0 1 6

Graph Theory Perfect Matchings in Complete graphs q K 2 n+1 has no perfect matching, Consider K 2 n. – Let fn be the number of ways to pair up 2 n distinct people in K 2 n – There are 2 n-1 choices for partner of v 2 n, and for each such choices there are fn-1 ways to complete the matching (see example in the next page) – Hence fn=(2 n-1)fn-1 for n 1. With f 0=1, it follows by induction that fn=(2 n-1)·(2 n-3) · · ·(1). Ch. 3. Matchings and Factors 7

Graph Theory Example: Perfect Matchings in K 6 q For K 6 , n=3, – f 3 is the number of perfect matchings – f 3= (2 n-1) * f 2 = 5* f 2=5*3*f 1 Ch. 3. Matchings and Factors 8

Graph Theory Maximal Matching and Maximum Matching 3. 1. 4 q A maximum matching in a graph is matching that can not be enlarged by adding an edge. – A maximum matching is a matching of maximum size among all matchings in the graph. q A matching M is maximal if every edge not in M is incident to an edge already in M. – Every maximum matching is a maximal matchings, but the converse need not hold. Ch. 3. Matchings and Factors 9

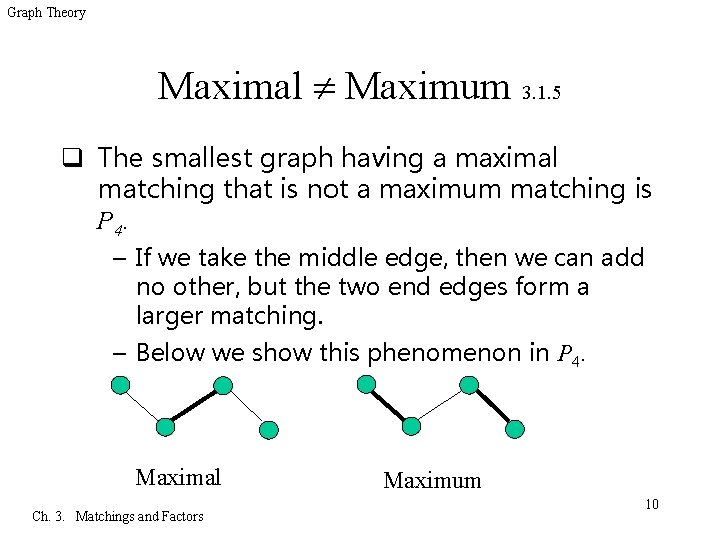
Graph Theory Maximal Maximum 3. 1. 5 q The smallest graph having a maximal matching that is not a maximum matching is P 4. – If we take the middle edge, then we can add no other, but the two end edges form a larger matching. – Below we show this phenomenon in P 4. Maximal Ch. 3. Matchings and Factors Maximum 10

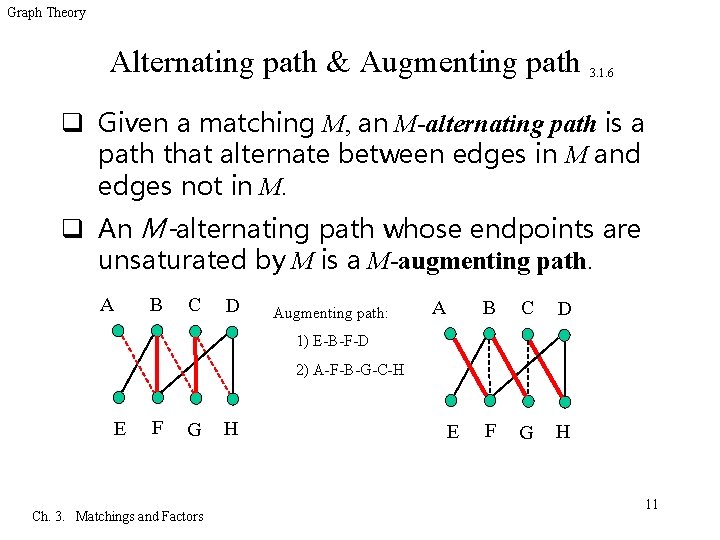
Graph Theory Alternating path & Augmenting path 3. 1. 6 q Given a matching M, an M-alternating path is a path that alternate between edges in M and edges not in M. q An M-alternating path whose endpoints are unsaturated by M is a M-augmenting path. B A C D Augmenting path: A B C D F G H 1) E-B-F-D 2) A-F-B-G-C-H E F G Ch. 3. Matchings and Factors H E 11

Graph Theory Symmetric Difference 3. 1. 7 q If G and H are graphs with vertex set V, then the symmetric difference G H is the graph with vertex set V whose edges are those edges appearing in exactly one of G and H. q We also use this notation for sets of edges ; in particular, if M and M’ are matchings, then M M’ = (M-M’) (M’-M). q Very similar to Exclusive-OR Ch. 3. Matchings and Factors 12

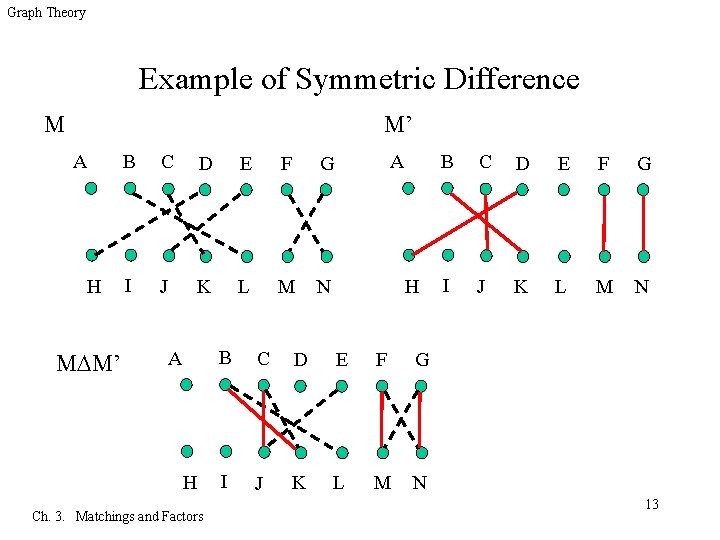
Graph Theory Example of Symmetric Difference M M’ A H M M’ B C D E F G I J K L M N A H Ch. 3. Matchings and Factors A H B C D E F G I J K L M N 13

Graph Theory Lemma: Every component of the symmetric difference of two matchings is a path or an even cycle 3. 1. 9 Proof: q Let M and M’ be matchings, and F be M M’. q Since M and M’ are matchings, every vertex has at most one incident edge from each of them q Thus F has at most two edges at each vertex. q Since (F) 2, every component of F is a path or a cycle. A B C D E F G I J K L M N M M’ H Ch. 3. Matchings and Factors 14

Graph Theory Lemma: Every component of the symmetric difference of two matchings is a path or an even cycle 3. 1. 9 Proof: (continue) q Furthermore, every path or cycle in F alternates between edges M-M’ and edges of M’-M. q Thus each cycle has even length, with an equal number of edges from M and from M’. Ch. 3. Matchings and Factors 15

Graph Theory Theorem: A matching M in a graph G is a maximum matching in G if and only if G has no M-augmenting path. 3. 1. 10 Proof: q We prove the contrapositive of each direction; G has a matching larger than M if and only if G has an Maugmenting path. q (sufficiency) It is seen that an M-augmenting path can be used to produce a matching larger than M. Ch. 3. Matchings and Factors 16

Graph Theory Theorem: A matching M in a graph G is a maximum matching in G if and only if G has no M-augmenting path. 3. 1. 10 Proof: (continue) q (necessity) For the converse, – Let M’ be a matching in G larger than M – Let F=M M’. By Lemma 3. 1. 9, F consists of paths and even cycles; the cycles have the same number of edges from M and M’ – Since |M’|>|M|, F must have a component with more edges of M’ than of M. Such a component can only be a path that starts and ends with an edge of M’; thus it is a Maugmenting path in G. Ch. 3. Matchings and Factors 17

Graph Theory Theorem: An X, Y-bigraph G has a matching that saturates X if and only if |N(S)| |S| for all S X. 3. 1. 11 q Necessity. The |S| vertices matched to S must lie in N(S). q Sufficiency. To prove that Hall’s Condition is sufficient, we prove the contra-positive: If M is a maximum matching in G and M does not saturate X, then there is a set S X such that |N(S)|<|S|. Ch. 3. Matchings and Factors 18

Graph Theory Theorem: An X, Y-bigraph G has a matching that saturates X if and only if |N(S)| |S| for all S X. 3. 1. 11 Sufficiency q Let u X be a vertex unsaturated by M. q Among all the vertices reachable from u by Malternating paths in G, let S consist of those in X, and that T consist of those in Y. → Given u, Let ‘~’ represent alternating Let R ={v| (v, u) M~Path exists} S={v|v X and v R} T={v|v Y and v R} X u S Y T=N(S) Ch. 3. Matchings and Factors 19

Graph Theory Theorem 3. 1. 11 Sufficicy Continue q We claim that M matches T with S-{u}. The Malternating paths from u reach Y along edges not in M and return to X along edges in M. q Hence every vertex of S-{u} is reached by an edge in M from a vertex in T. S X u Y Ch. 3. Matchings and Factors T=N(S) 20

Graph Theory Theorem 3. 1. 11 Continue Sufficiency continue q Since there is no M-augmenting path, every vertex of T is saturated; thus an M-augmenting path reaching y T extends via M to a vertex of S. q Hence these edges of M yield a bijection from T to S{u}, and we have |T|=|S-{u}|. S X u Y Ch. 3. Matchings and Factors T=N(S) 21

Graph Theory Theorem 3. 1. 11 Continue Sufficiency continue q With T=N(S), we have proved that |N(S)|=|T|=|S|-1<|S| for this choice of S. This completes the proof of the contrapositive. S X u Y Ch. 3. Matchings and Factors T=N(S) 22

Graph Theory Corollary: for k>0, every k-regular bipartite graph has a perfect matching. 3. 1. 13 Proof : q Let G be a k-regular X, Y- bigraph q Counting the edges by endpoints in X and by endpoints in Y shows that k|X| = k|Y| q So |X|=|Y|. q Hence it suffices to verify Hall’s Condition; a matching that saturates X will also saturate Y and be perfect matching. ► Ch. 3. Matchings and Factors 23

Graph Theory Corollary: for k>0, every k-regular bipartite graph has a perfect matching. 3. 1. 13 Proof : Continued q Consider S X. Let m be the number of edges from S to N(S) q Since G is k-regular, m=k|S|. These m edges are incident to N(S), so m k|N(S)| N(S) S m=k|S|, Ch. 3. Matchings and Factors m k|N(S)| 24

Graph Theory Corollary: for k>0, every k-regular bipartite graph has a perfect matching. 3. 1. 13 Proof : Continued q Hence k|S| k|N(S)|, which yields |N(S)| |S| when k>0. q Having chosen S X arbitrarily, we have established Hall’s condition. N(S) S m=k|S|, Ch. 3. Matchings and Factors m k|N(S)| 25

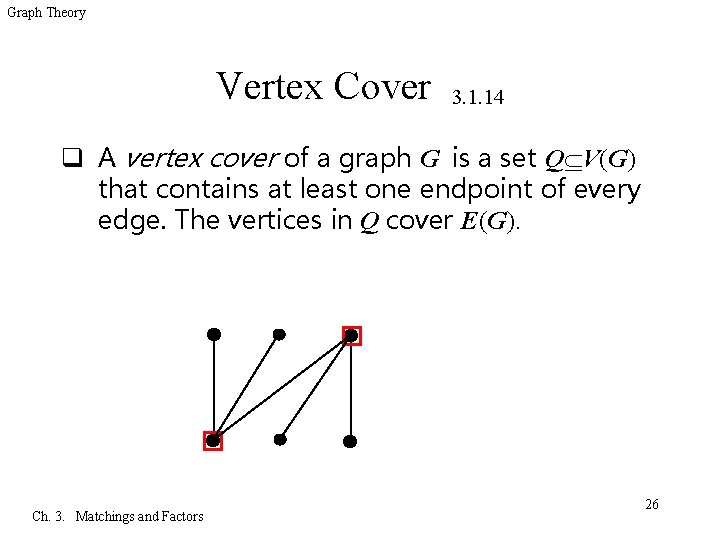
Graph Theory Vertex Cover 3. 1. 14 q A vertex cover of a graph G is a set Q V(G) that contains at least one endpoint of every edge. The vertices in Q cover E(G). Ch. 3. Matchings and Factors 26

Graph Theory Vertex Cover 3. 1. 14 q In a graph that represents a road network (with straight roads and no isolated vertices). – Finding a minimum vertex cover = Placing the minimum number of policemen to guard the entire road network. Ch. 3. Matchings and Factors 27

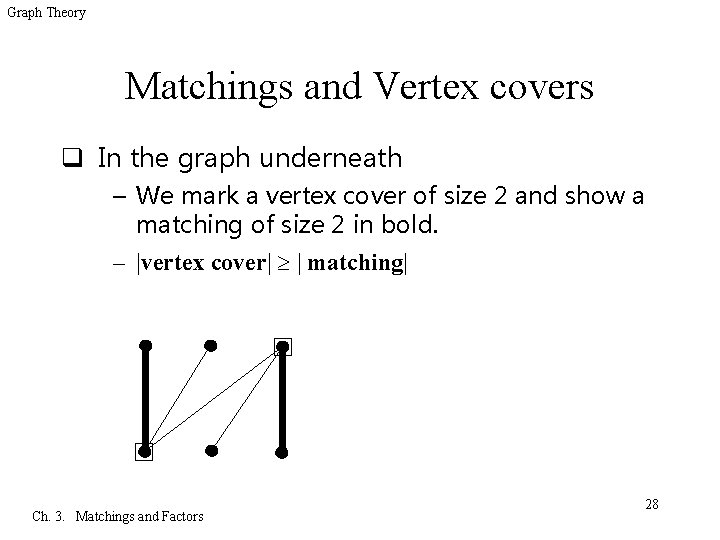
Graph Theory Matchings and Vertex covers q In the graph underneath – We mark a vertex cover of size 2 and show a matching of size 2 in bold. – |vertex cover| | matching| Ch. 3. Matchings and Factors 28

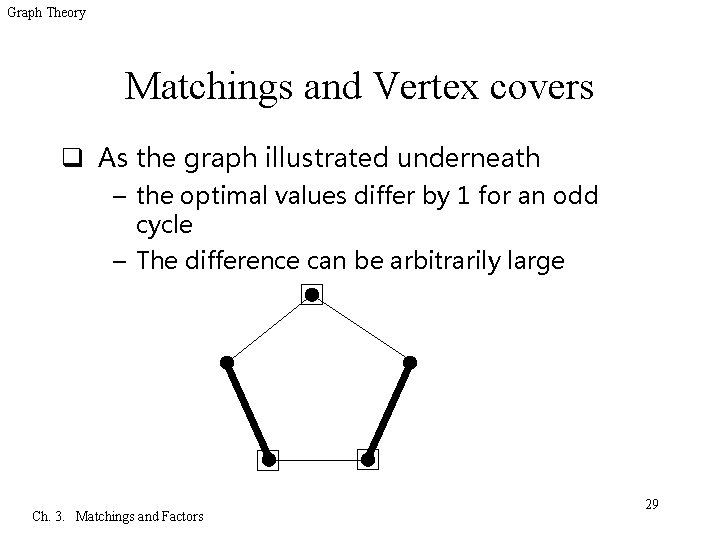
Graph Theory Matchings and Vertex covers q As the graph illustrated underneath – the optimal values differ by 1 for an odd cycle – The difference can be arbitrarily large Ch. 3. Matchings and Factors 29

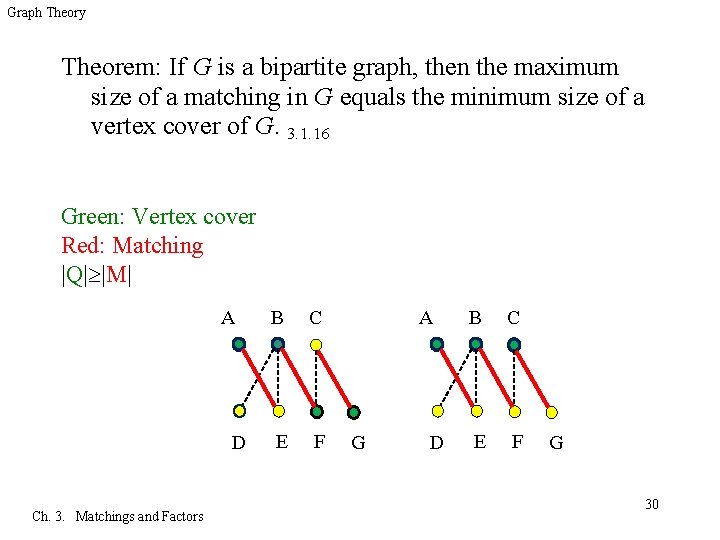
Graph Theory Theorem: If G is a bipartite graph, then the maximum size of a matching in G equals the minimum size of a vertex cover of G. 3. 1. 16 Green: Vertex cover Red: Matching |Q| |M| A D Ch. 3. Matchings and Factors B C E F A G D B C E F G 30

Graph Theory Theorem 3. 1. 16 Proof : q Let G be an X, Y-bigraph. q Since distinct vertices must be used to cover the edges of a matching, |Q| |M| whenever Q is a vertex cover and M is a matching in G q Given a smallest vertex cover Q of G, we construct a matching of size |Q| to prove that equality can always be achieved. Ch. 3. Matchings and Factors 31

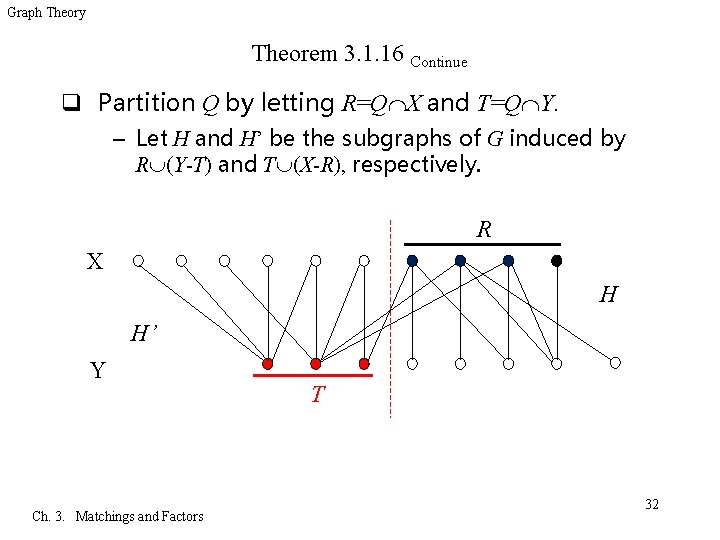
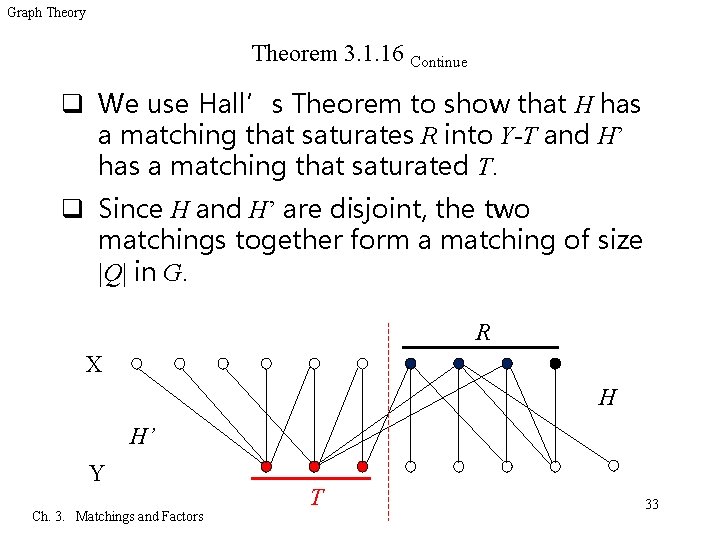
Graph Theory Theorem 3. 1. 16 Continue q Partition Q by letting R=Q X and T=Q Y. – Let H and H’ be the subgraphs of G induced by R (Y-T) and T (X-R), respectively. R X H H’ Y Ch. 3. Matchings and Factors T 32

Graph Theory Theorem 3. 1. 16 Continue q We use Hall’s Theorem to show that H has a matching that saturates R into Y-T and H’ has a matching that saturated T. q Since H and H’ are disjoint, the two matchings together form a matching of size |Q| in G. R X H H’ Y Ch. 3. Matchings and Factors T 33

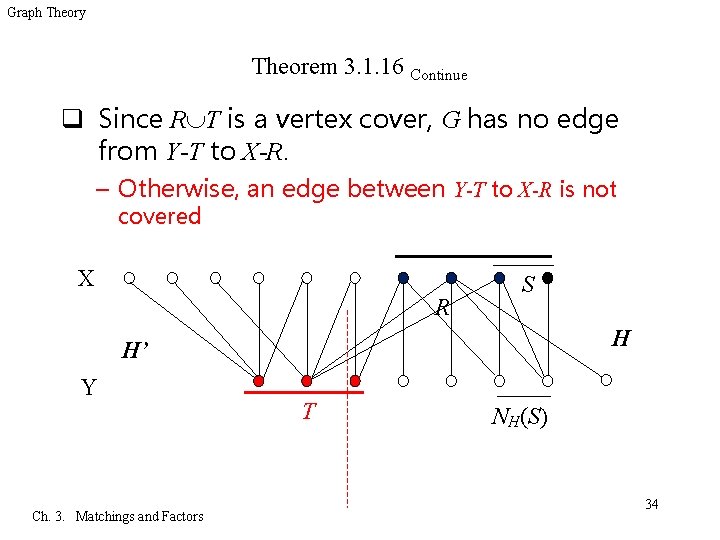
Graph Theory Theorem 3. 1. 16 Continue q Since R T is a vertex cover, G has no edge from Y-T to X-R. – Otherwise, an edge between Y-T to X-R is not covered X R S H H’ Y Ch. 3. Matchings and Factors T NH(S) 34

Graph Theory Theorem 3. 1. 16 Continue q For each S R, we consider NH(S), which is contained in Y-T. – If |NH(S)|<|S|, then we can substitute NH (S) for S in Q to obtain a smaller vertex cover – since NH(S) cover all edges incident to S that are not covered by T R X S H H’ Y Ch. 3. Matchings and Factors |NH(S)| |S| T NH (S) 35

Graph Theory Theorem 3. 1. 16 continue q The minimality of Q thus yields Hall’s Condition in H, and hence H has a matching that saturates R q Applying the same argument to H’ yields the matching that saturates T R X S H H’ Y T A matching exists in H’ of size |T| Ch. 3. Matchings and Factors NH(S) A matching exists in H of size |R| 36

Graph Theory Min-Max relation 3. 1. 17 q A min-max relation is a theorem stating equality between the answers to a minimization problem and maximization problem over a class of instances. q The Konig-Egervary Theorem is such a relation for vertex covering and matching in bipartite graphs. Ch. 3. Matchings and Factors 37

Graph Theory Min-Max relation 3. 1. 17 q For the discussions in this text, we think of a dual pair of optimization problems – as a maximization problem M and minimization problem N, defined on the same instances (such as graphs), – such that for every candidate solution M to M and every candidate N to N, the number of M is less than or equal to the value of N. – Often the “value” is cardinality, as above where M is maximum matching and N is minimum vertex cover. Ch. 3. Matchings and Factors 38

Graph Theory Independent sets and covers q The independence number of a graph is the maximum size of an independent set of vertices. q The independence number of a bipartite graph does not always equal the size of a partite set. – In the graph bellow, both partite sets have size 3, but we have marked an independent set of size 4. Ch. 3. Matchings and Factors 39

Graph Theory Edge cover 3. 1. 19 q An edge cover of G is a set L of edges such that every vertex of G is incident to some edge of L. – The four bold edges in thee following graph form an edge cover. Ch. 3. Matchings and Factors 40

Graph Theory Definitions q For the optimal sizes of the sets of the independence and covering problems we have defined, we use the notation below. – Maximum size of independent set (G) – Maximum size of matching – Minimum size of vertex cover – Minimum size of edge cover Ch. 3. Matchings and Factors ’(G) 41

Graph Theory Lemma: In a graph G, S V(G) is an independent set if and only if Ŝ is a vertex cover, and hence (G)+ (G) = n(G). 3. 1. 21 Proof : q If S is an independent set, then every edge is incident to at least one vertex of Ŝ. q Conversely, if Ŝ covers all the edges, then there are no edges joining vertices of S. � Independent set Ch. 3. Matchings and Factors 42

Graph Theory Lemma: In a graph G, S V(G) is an independent set if and only if Ŝ is a vertex cover, and hence (G)+ (G) = n(G). 3. 1. 21 Proof : continued q Hence every maximum independent set is the complement of a minimum vertex cover, and (G)+ (G)=n(G) = 4 (G) = 2 n(G) = 6 Ch. 3. Matchings and Factors 43

Graph Theory Theorem: If G is a graph without isolated vertices, then α’(G)+ β’(G) =n(G). 3. 1. 22 ’(G): Maximum size of matching ’(G): Minimum size of edge cover Proof: q From a maximum matching M, we will construct an edge cover of size n(G)-|M|. (see next page) – Since a smallest edge cover is not bigger than this cover, this will imply that ’(G) n(G)- ’(G). q Also, from a minimum edge cover L, we will construct a matching of size n(G)-|L|. (see next page) – Since a largest matching is not smaller than this matching, this will imply that ’(G) n(G)- ’(G). q These two inequalities complete the proof. (detail) Ch. 3. Matchings and Factors 44

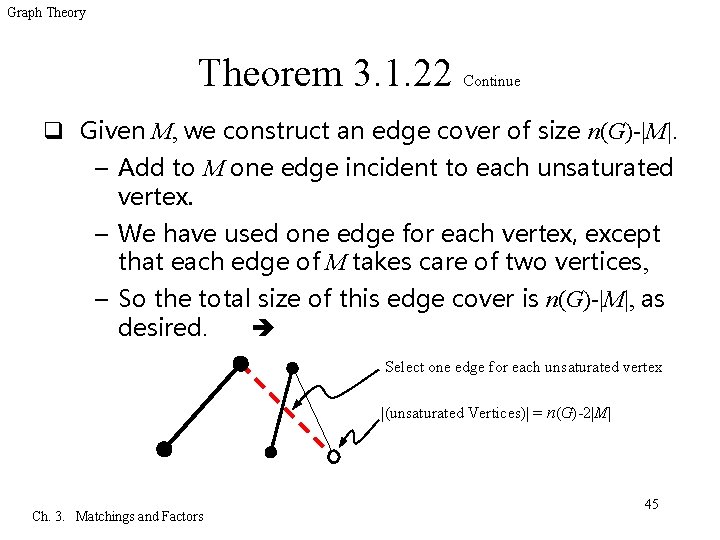
Graph Theory Theorem 3. 1. 22 Continue q Given M, we construct an edge cover of size n(G)-|M|. – Add to M one edge incident to each unsaturated vertex. – We have used one edge for each vertex, except that each edge of M takes care of two vertices, – So the total size of this edge cover is n(G)-|M|, as desired. Select one edge for each unsaturated vertex |(unsaturated Vertices)| = n(G)-2|M| Ch. 3. Matchings and Factors 45

Graph Theory Theorem 3. 1. 22 Continue q Given a minimum edge cover L, we construct a matching of size n(G)-|L|. – If both ends of an edge e belong to edges in L other than e, then e L, since L-{e} is also an edge cover. – Hence each component formed by edges of L has at most one vertex of degree exceeding 1 and is a star (a tree with at most one non-leaf). can be deleted Assume k components, then |L|=n(G)-k Impossible case Ch. 3. Matchings and Factors One component 46

Graph Theory Theorem 3. 1. 22 Continue – Let k be the number of these components – Since L has one edge for each non-central vertex in each star, we have |L|=n(G)-k – We form a matching M of size k =n(G)-|L| by choosing one edge from each star in L Ch. 3. Matchings and Factors 47

Graph Theory Maximum Bipartite Matching 3. 2 q To find a maximum matching, we iteratively seek augmenting paths to enlarge the current matching. q Given a matching M in an X, Y –bigraph G, we search for M-augmenting paths from each Munsaturated vertex in X. Ch. 3. Matchings and Factors 48

Graph Theory Augmenting Path Algorithm – for matching 3. 2. 1 Input: An X, Y-bigraph G, a matching M in G, and the set U of M-unsaturated vertices in X. Ideal: 1. Explore M-alternating paths from U 2. Let S X and T Y be the sets of vertices reached 3. Mark vertices of S that have been explored for path extensions 4. As a vertex is reached, record the vertex from which it is reached Ch. 3. Matchings and Factors 49

Graph Theory Augmenting Path Algorithm – for matching 3. 2. 1 Initialization: S=U and T=. Iteration: q If S has no unmarked vertex, stop and report – T (X-S) as a minimum cover and – M as a maximum matching Ch. 3. Matchings and Factors 50

Graph Theory Augmenting Path Algorithm – for matching 3. 2. 1 Iteration: (continue) q Otherwise, select an unmarked x S. To explore x, consider each y N(x) such that xy M. – If y is unsaturated, terminate and report an Maugmenting path from U to y – Otherwise, y is matched to some w X by M. In this case, include y in T (reached from x) and include w in S (reached from y) – After exploring all such edges incident to x, mark x and iterate Ch. 3. Matchings and Factors 51

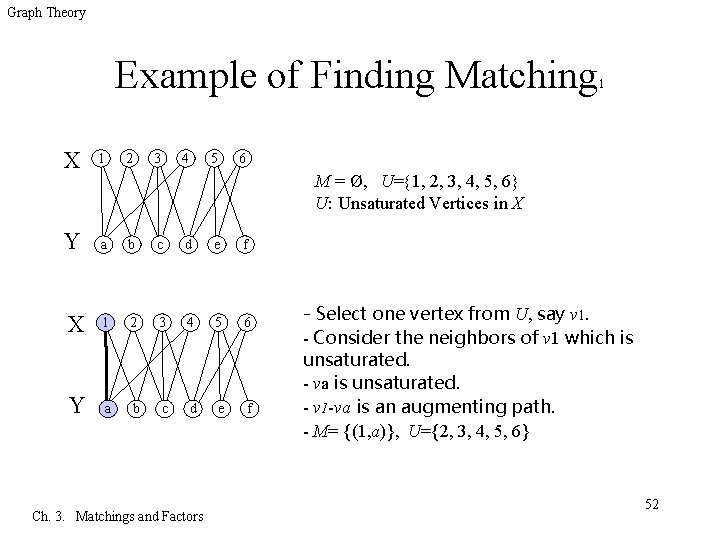
Graph Theory Example of Finding Matching X 1 Y a b c d e f X 1 2 3 4 5 6 Y a b c d e f 2 3 4 5 1 6 M = Ø, U= 1, 2, 3, 4, 5, 6 U: Unsaturated Vertices in X Ch. 3. Matchings and Factors - Select one vertex from U, say v 1. - Consider the neighbors of v 1 which is unsaturated. - va is unsaturated. - v 1 -va is an augmenting path. - M= {(1, a)}, U={2, 3, 4, 5, 6} 52

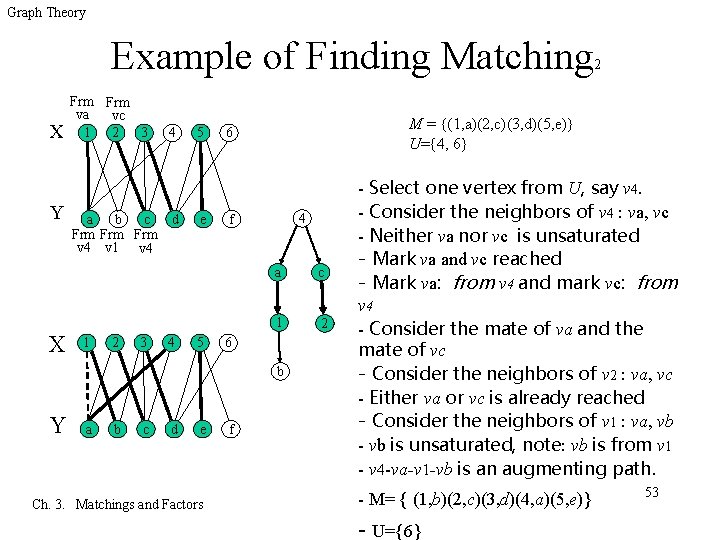
Graph Theory Example of Finding Matching X Y X Frm va vc 1 2 3 a b c Frm Frm v 4 v 1 v 4 1 2 3 4 d 4 5 e 5 M = {(1, a)(2, c)(3, d)(5, e)} U= 4, 6 6 4 f a c 1 2 6 b Y a b c d e Ch. 3. Matchings and Factors f 2 - Select one vertex from U, say v 4. - Consider the neighbors of v 4 : va, vc - Neither va nor vc is unsaturated - Mark va and vc reached - Mark va: from v 4 and mark vc: from v 4 - Consider the mate of va and the mate of vc - Consider the neighbors of v 2 : va, vc - Either va or vc is already reached - Consider the neighbors of v 1 : va, vb - vb is unsaturated, note: vb is from v 1 - v 4 -va-v 1 -vb is an augmenting path. - M= { (1, b)(2, c)(3, d)(4, a)(5, e)} - U={6} 53

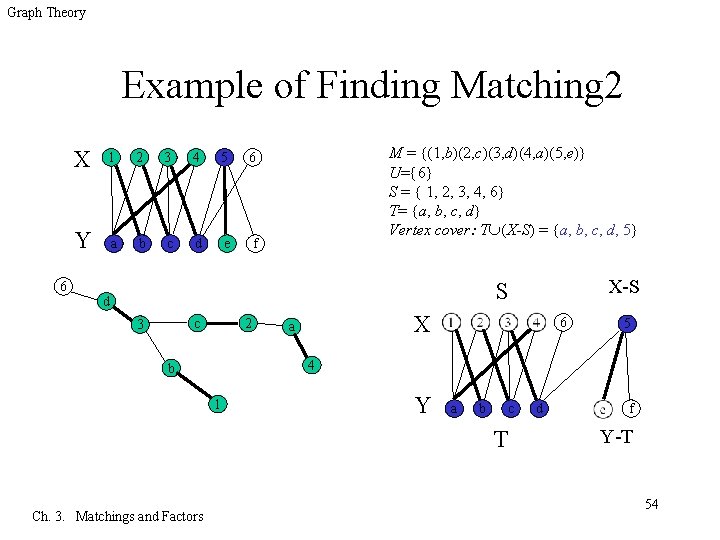
Graph Theory Example of Finding Matching 2 6 X 1 2 3 4 5 6 Y a b c d e f M = {(1, b)(2, c)(3, d)(4, a)(5, e)} U= 6 S = { 1, 2, 3, 4, 6} T= {a, b, c, d} Vertex cover: T (X-S) = {a, b, c, d, 5} X-S S d c 3 2 X a 6 4 b 1 Y a b c T Ch. 3. Matchings and Factors 5 d f Y-T 54

Graph Theory Theorem: Repeatedly applying the augmenting path algorithm to a bipartite graph produces a matching and a vertex cover of equal size. 3. 2. 2 Proof: q We need only verify that the Augmenting Path Algorithm produces an M-augmenting path or a vertex cover of size |M| – If the algorithm produces an M-augmenting path, we are finished. – Otherwise, it terminates by marking all vertices of S and claiming that R=T (X-S) is a vertex cover of size |M|. We prove that R is a vertex cover and has size |M|. Continued in the next page Ch. 3. Matchings and Factors 55

Graph Theory Theorem: Repeatedly applying the augmenting path algorithm to a bipartite graph produces a matching and a vertex cover of equal size. 3. 2. 2 Proof: (continue) q If the algorithm produces an M-augmenting path, we are finished. q Otherwise, it terminates by marking all vertices of S and claiming that R=T (X-S) is a vertex cover of size |M|. – We must prove that R is a vertex cover and has size |M|. Continued in the next page Ch. 3. Matchings and Factors 56

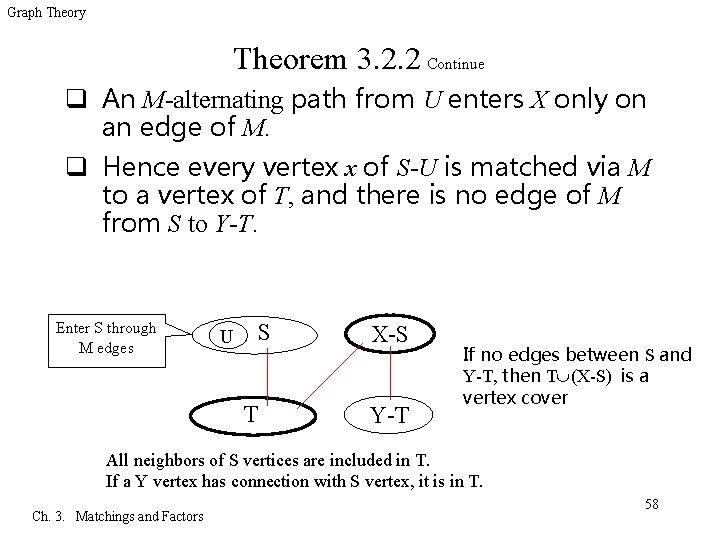
Graph Theory Theorem 3. 2. 2 Continue q To show that R=T (X-S) is a vertex cover, it suffices to show that there is no edge joining S to Y-T Enter S through M edges U S T X-S Y-T If no edges between S and Y-T, then T (X-S) is a vertex cover All neighbors of S vertices are included in T. If a Y vertex has connection with S vertex, it is in T. Ch. 3. Matchings and Factors 57

Graph Theory Theorem 3. 2. 2 Continue q An M-alternating path from U enters X only on an edge of M. q Hence every vertex x of S-U is matched via M to a vertex of T, and there is no edge of M from S to Y-T. Enter S through M edges U S T X-S Y-T If no edges between S and Y-T, then T (X-S) is a vertex cover All neighbors of S vertices are included in T. If a Y vertex has connection with S vertex, it is in T. Ch. 3. Matchings and Factors 58

Graph Theory Theorem 3. 2. 2 Continue q Also there is no such edge outside M. When the path reaches x S, it can continue along any edge not in M, and exploring x puts all other neighbors of x into T. q Since the algorithm marks all of S before terminating, all edges from S go to T. Ch. 3. Matchings and Factors 59

Graph Theory Weighted Bipartite Matching q Seek a matching of maximum total weight. q It is assumed that the given graph is Kn, n. – If the given graph is not a complete bipartite graph, insert edges with zero weight. Workers wk Jobs Ch. 3. Matchings and Factors 60

Graph Theory Examples of Weighted bipartite matching and its dual 3. 2. 5 q A farming company owns n farms and n processing plants. – Each farm can produce corn to the capacity of one plant. – The profit that results from sending the output of farm i to plant j is wi, j. – Placing weight wi, j on edge xiyj gives us a weighted bipartite graph with partite sets X={x 1, …, xn} and Y={y 1, …, yn}. – The company wants to select edges forming a matching to maximize total profit. Ch. 3. Matchings and Factors 61

Graph Theory Examples of Weighted bipartite matching and its dual q The government claims that too much corn is being produced, so it will pay the company not to process corn. – How to pay? – Pay minimum amount! Ch. 3. Matchings and Factors 62

Graph Theory Examples of Weighted bipartite matching and its dual q Payment regulation – The government will pay ui if the company agrees not to use farm i and vj if it agrees not to use plant j – If ui+vj<wi, j, then the company makes more by using the edge xiyj than by taking the government payments for those vertices. – In order to stop all production, the government must offer amounts such that ui+vj wi, j for all i, j. The governments wants to find such values to minimize ui+ vj. Ch. 3. Matchings and Factors 63

Graph Theory Traversal of an n-by-n matrix q A transversal of an n-by-n matrix consists of n positions, one in each row and each column. q Finding a transversal with maximum sum is the Assignment Problem. Ch. 3. Matchings and Factors 64

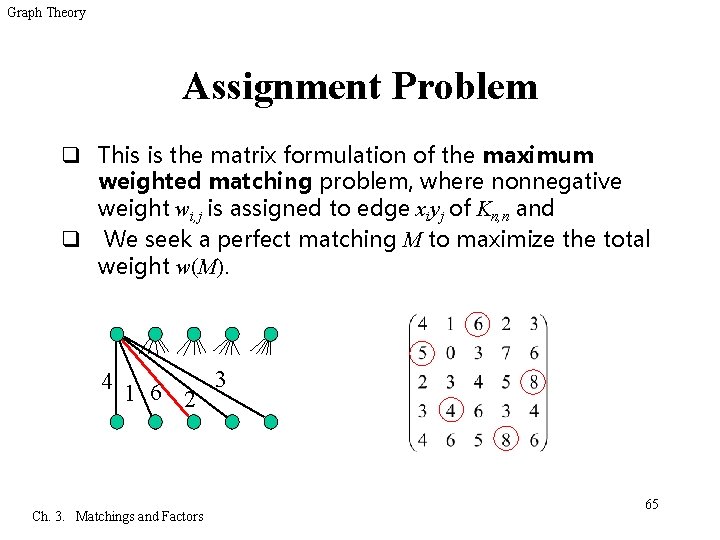
Graph Theory Assignment Problem q This is the matrix formulation of the maximum weighted matching problem, where nonnegative weight wi, j is assigned to edge xiyj of Kn, n and q We seek a perfect matching M to maximize the total weight w(M). 3 4 1 6 2 Ch. 3. Matchings and Factors 65

Graph Theory Minimum weighted Cover q With these weights, a (weighted) cover is a choice of labels ui, …, un and vj, …, vn such that ui+vj wi, j for all i, j. The cost c(u, v) for a cover (u, v) is ui+ vj. q The minimum weighted cover problem is that of finding a cover of minimum cost. 0 0 0 A cover, but not minimum Ch. 3. Matchings and Factors 6 7 8 66

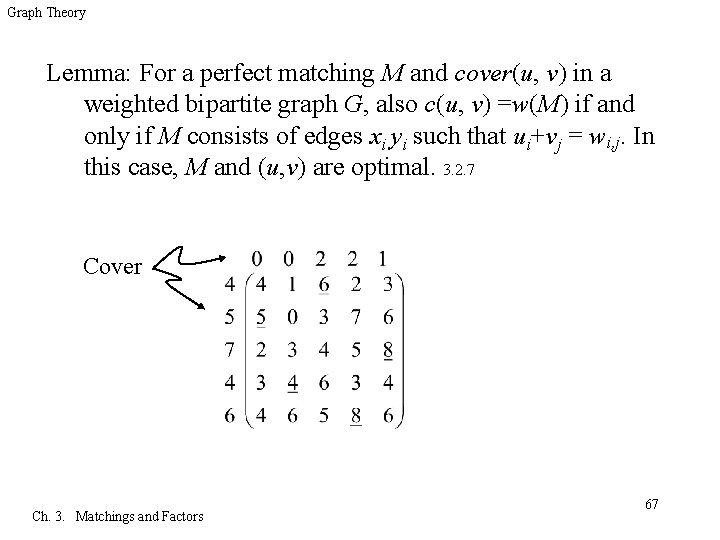
Graph Theory Lemma: For a perfect matching M and cover(u, v) in a weighted bipartite graph G, also c(u, v) =w(M) if and only if M consists of edges xi yi such that ui+vj = wi, j. In this case, M and (u, v) are optimal. 3. 2. 7 Cover Ch. 3. Matchings and Factors 67

Graph Theory Lemma: For a perfect matching M and cover(u, v) in a weighted bipartite graph G, also c(u, v) =w(M) if and only if M consists of edges xiyi such that ui+vj = wi, j. In this case, M and (u, v) are optimal. 3. 2. 7 Proof: q Since M saturates each vertex, summing the constraints ui+vj wi, j that arise from its edges yields c(u, v)=w(M), then equality must hold in each of the n inequalities summed. q Finally, since c(u, v) w(M) for every matching and every cover, c(u, v)=w(M) implies that there is no matching with weight greater than c(u, v) and no cover with cost less than w(M). Ch. 3. Matchings and Factors 68

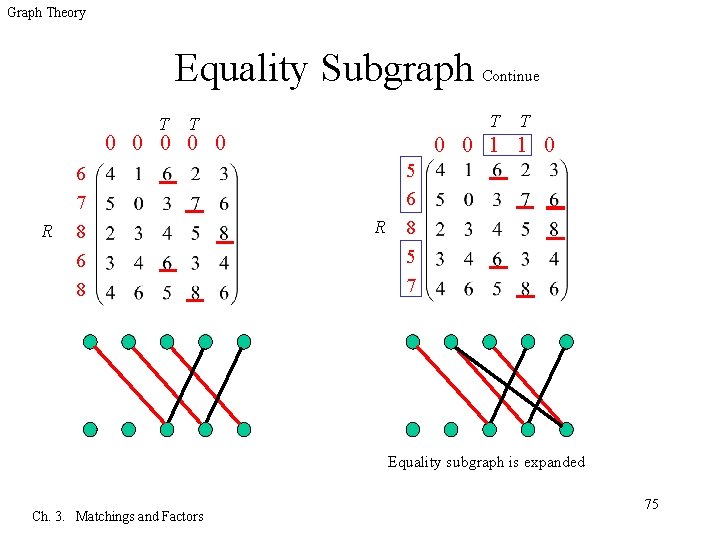
Graph Theory Equality subgraph 3. 2. 8 q The equality subgraph Gu, v for a cover (u, v) is the spanning subgraph of Kn, n having the edges xiyj such that ui+vj=wi, j. Y 0 0 0 X 6 7 8 6 8 Ch. 3. Matchings and Factors X Y 69

Graph Theory Equality Subgraph 3. 2. 8 q If Gu, v has a perfect matching, then its weight is ui+ vj, and by Lemma 3. 2. 7 we have the optimal solution. Ch. 3. Matchings and Factors 70

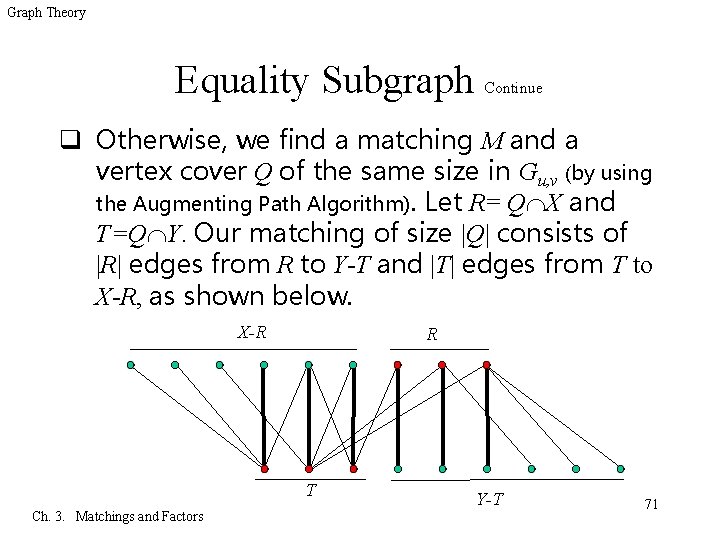
Graph Theory Equality Subgraph Continue q Otherwise, we find a matching M and a vertex cover Q of the same size in Gu, v (by using the Augmenting Path Algorithm). Let R= Q X and T=Q Y. Our matching of size |Q| consists of |R| edges from R to Y-T and |T| edges from T to X-R, as shown below. X-R R T Ch. 3. Matchings and Factors Y-T 71

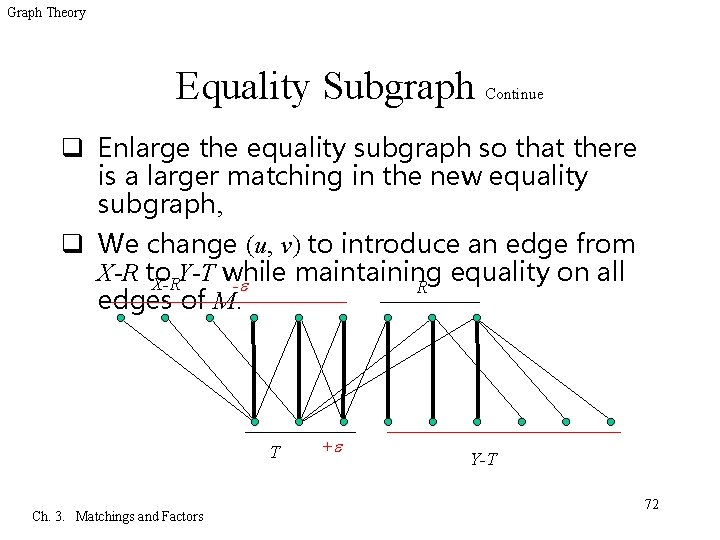
Graph Theory Equality Subgraph Continue q Enlarge the equality subgraph so that there is a larger matching in the new equality subgraph, q We change (u, v) to introduce an edge from X-R to Y-T while maintaining equality on all X-R - R edges of M. T Ch. 3. Matchings and Factors + Y-T 72

Graph Theory Equality Subgraph Continue q A cover requires ui+vj wi, j for all i, j; the difference ui+vj-wi, j is the excess for i, j. q Edges joining X-R and Y-T are not in Gu, v and have positive excess. T T 0 0 0 6 7 R 8 6 8 Ch. 3. Matchings and Factors 6 7 0 0 R∪T: Vertex Cover R 8 6 8 0 T 0 73

Graph Theory Equality Subgraph Continue q Let be the minimum excess on the edges from X-R to Y-T. Reduce ui by for all xi X-R q To maintain the cover condition for these edges while bringing at least one into the equality subgraph – Increase vj by for yj T – To maintain T T the cover condition. Tfor T the edges from XR 0 to 0 T 0 0 0 0 R 6 7 8 6 8 Ch. 3. Matchings and Factors 6 2 5 0 4 3 7 2 7 4 0 1 R 8 6 5 4 3 0 6 3 2 0 3 2 Matrix of excess Min excess ε = 1 8 4 2 3 0 2 74

Graph Theory Equality Subgraph T T T 0 0 0 R 6 7 8 6 8 Continue T 0 0 1 1 0 R 5 6 8 5 7 Equality subgraph is expanded Ch. 3. Matchings and Factors 75

Graph Theory Equality Subgraph Continue q Repeat the procedure with the new equality subgraph; eventually we obtain a cover whose equality subgraph has a perfect matching. Ch. 3. Matchings and Factors 76

Graph Theory Hungarian Algorithm 3. 2. 9 Input: A matrix of weights on the edges of Kn, n with bipartition X, Y. Idea: Iteratively adjusting the cover (u, v) until the equality subgraph Gu, v has a perfect matching. Initialization: Let (u, v) be a cover, such as ui=maxj wi, j and vj=0. Ch. 3. Matchings and Factors 77

Graph Theory Hungarian Algorithm Continue Iteration: q Find a maximum matching M in Gu, v. – If M is a perfect matching, stop and report M as a maximum weight matching. – Otherwise, • Let Q be a vertex cover of size |M| in Gu, v. • Let R=X Q and T=Y Q. • Let =min{ui+vj-wi, j: xi X-R, yj Y-T}. • Decrease ui by for xi X-R, and • increase vj by for yj T. – Form the new equality subgraph and repeat. Ch. 3. Matchings and Factors 78

Graph Theory Solving the Assignment Problem 3. 2. 10 q The first matrix below is the matrix of weights. q The others display a cover (u, v) and the corresponding excess matrix. T T Ch. 3. Matchings and Factors 79

Graph Theory Solving the Assignment Problem 3. 2. 10 q We underscore entries in the excess matrix to mark a maximum matching M of Gu, v, which appears as bold edges in the equality subgraphs drawn for the first two excess matrices. (Drawing the equality subgraphs is not necessary. ) X Y T T Ch. 3. Matchings and Factors R T T 80

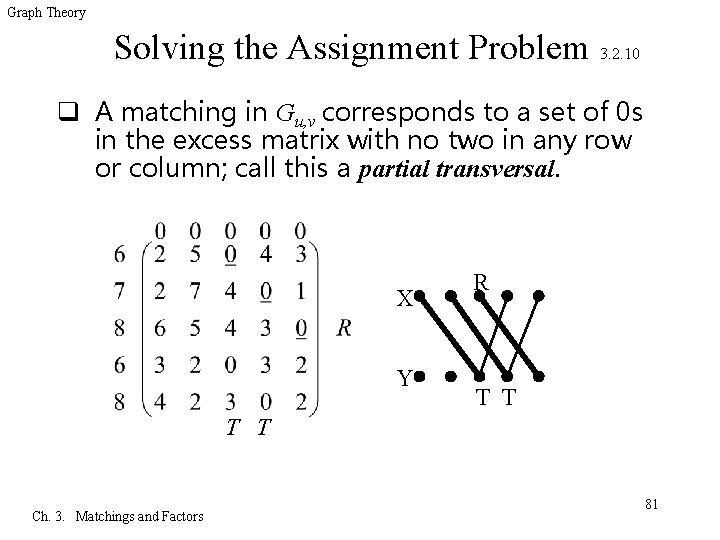
Graph Theory Solving the Assignment Problem 3. 2. 10 q A matching in Gu, v corresponds to a set of 0 s in the excess matrix with no two in any row or column; call this a partial transversal. X Y R T T Ch. 3. Matchings and Factors 81

Graph Theory Solving the Assignment Problem q A set of rows and columns covering the 0 s in the excess matrix is a covering set q This corresponds to a vertex cover in Gu, v. q A covering set of size less than n yields progress toward a solution, since the next weighted cover costs less. Ch. 3. Matchings and Factors 82

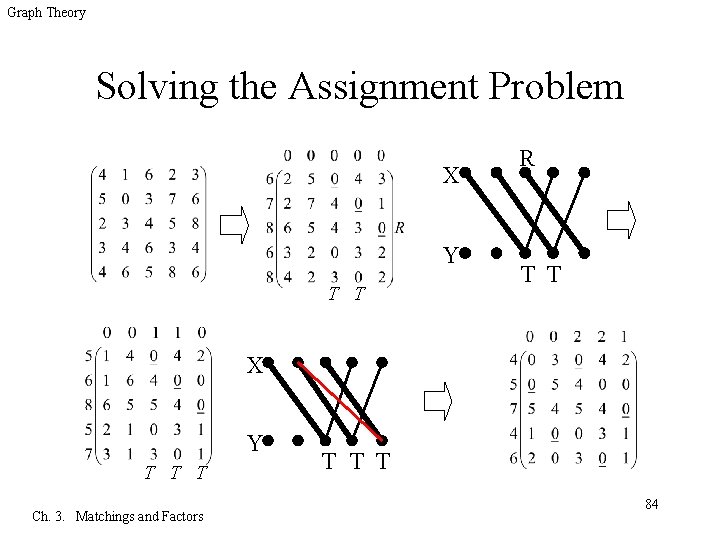
Graph Theory Solving the Assignment Problem q We study the 0 s in the excess matrix and find a partial transversal and a covering set of the same size. – In a small matrix, we can do this by inspection. Ch. 3. Matchings and Factors 83

Graph Theory Solving the Assignment Problem X Y T T R T T X Y T T T Ch. 3. Matchings and Factors T T T 84

Graph Theory Theorem: The hungarian Algorithm finds a maximum weight matching and a minimum cost cover. 3. 2. 11 q The algorithm – Begins with a cover. – Terminates only when the equality subgraph has a perfect matching, which guarantees equal value for the current matching and cover. q Suppose that (u, v) is the current cover and that the equality subgraph has no perfect matching. q Let (u’, v’) denote the new lists of numbers assigned to the vertices. Because is the minimum of a nonempty finite set of positive numbers, >0. Ch. 3. Matchings and Factors 85

Graph Theory Theorem 3. 2. 11 Continue q We verify first that (u’, v’) is a cover. – The change of labels on vertices of X-R and T yields ui’+vj’=ui+vj for edges xiyj from X-R to T or from R to Y-T. – If xi R and yi T, then ui’+vj’=ui+vj+ , and the weight remains covered. – If xi X-R and yj Y-T, then ui’+vj’ equals ui+vj- , which by the choice of is at least wi, j. X-R - R T + Ch. 3. Matchings and Factors Y-T 86

Graph Theory Theorem 3. 2. 11 Continue q The algorithm terminates only when the equality subgraph has a perfect matching, so it suffices to show that it does terminate. q Suppose that the weights wi, j are rational. Multiplying the weights by their least common denominator yields an equivalent problem with integer weights. Ch. 3. Matchings and Factors 87

Graph Theory Theorem 3. 2. 11 Continue q We can now assume that the labels in the current cover also are integers. q Thus each excess is also an integer, and at each iteration we reduce the cost of the cover by an integer amount. q Since the cost starts at some value and is bounded bellow by the weight of a perfect matching, after finitely many iterations we have equality. Ch. 3. Matchings and Factors 88

Graph Theory Factor q A factor of graph G is a spanning subgraph of G. – A k-factor is a spanning k-regular subgraph. – An odd component of a graph is a component of odd order; the number of odd components of H is o(H). q A 1 -factor and a perfect matching are almost the same thing. G Ch. 3. Matchings and Factors 1 -factor 89

Graph Theory Tutte’s 1 -factor Theorem q Tutte found a necessary and sufficient condition for which graphs have 1 -factors. – If G has a 1 -factor and we consider a set S V(G), then every odd component of G-S has a vertex matched to something outside it, which can only belong to S. – Since these vertices of S must be distinct, o(GS) |S|. q Tutte’s Condition: For all S V(G), o(G-S) |S|. – Tutte proved that this obvious necessary condition is also sufficient (TONCAS). Ch. 3. Matchings and Factors 90

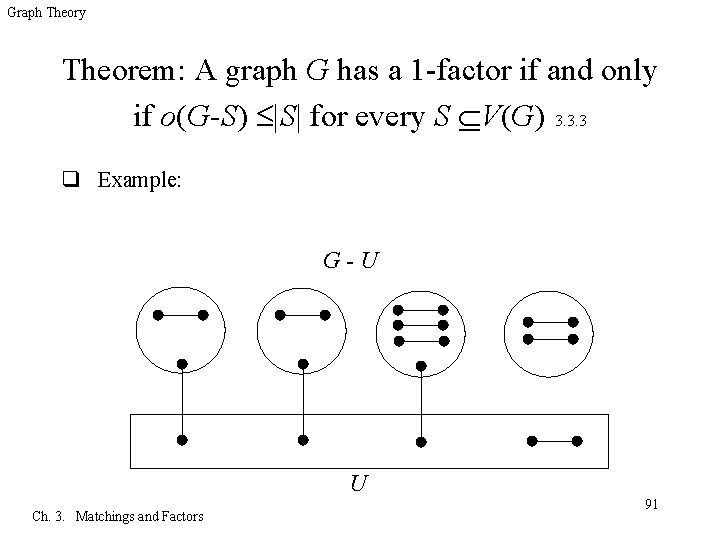
Graph Theory Theorem: A graph G has a 1 -factor if and only if o(G-S) |S| for every S V(G) 3. 3. 3 q Example: G-U U Ch. 3. Matchings and Factors 91

Graph Theory Join 3. 3. 6 q The join of simple graphs G and H, written G H, is the graph obtained from the disjoint union G+H by adding the edges {xy : x V(G), y V(H)}. P 4 K 3 Ch. 3. Matchings and Factors 92

Graph Theory Corollary: The largest number of vertices saturated by a matching in G is min s v(G) {n(G)-d(S)}, where d(S) = o(G-S) - |S|. 3. 3. 7 Proof: q Given S V(G), at most |S| edges can match vertices of S to vertices in odd components of G-S, so every matching have at least o(G-S)-|S| unsaturated vertices. We want to achieve this bound. q Let d=max{o(G-S)-|S|: S V(G)}. The case S= yields d 0. Let G’=G Kd. Since d(S) has the same parity as n(G) for each S, we know that n(G’) is even. If G’ satisfies Tutte’s Condition, then we obtain a matching of the desired size in G from a perfect matching in G’, because deleting the d added vertices eliminates edges that saturate at most d vertices of G. Ch. 3. Matchings and Factors 93

Graph Theory Corollary 3. 3. 7 continue q The condition o(G’-S’) |S’| holds for S’= because n(G’) is even. q If S’ is nonempty but does not contain all of Kd, then G’-S’ has only one component, and 1<|S’|. q Finally, when Kd S’, we let S=S’-V(Kd). We have G’-S’=G-S, so o(G’-S’)=o(G-S) |S|+d=|S’|. q We have verified that G’ satisfies Tutte’s Condition Ch. 3. Matchings and Factors 94

Graph Theory Edmonds’ Blossom Algorithm q In bipartite graphs, we can search quickly for augmenting paths (Algorithm 3. 2. 1) because we explore from each vertex at most once. q An M-alternating path from u can reach a vertex x in the same partite set as u only along a saturated edge. Hence only once can we search and explore x. B A C D Augmenting path: A-F-B-G-C-H The path arrives at B and C along saturated edges FB and GC, respectively E F G Ch. 3. Matchings and Factors H 95

Graph Theory Edmonds’ Blossom Algorithm q This property fails in graphs with odd cycles, because M-alternating paths from an unsaturated vertex may reach x both along saturated and along unsaturated edges. Ch. 3. Matchings and Factors 96

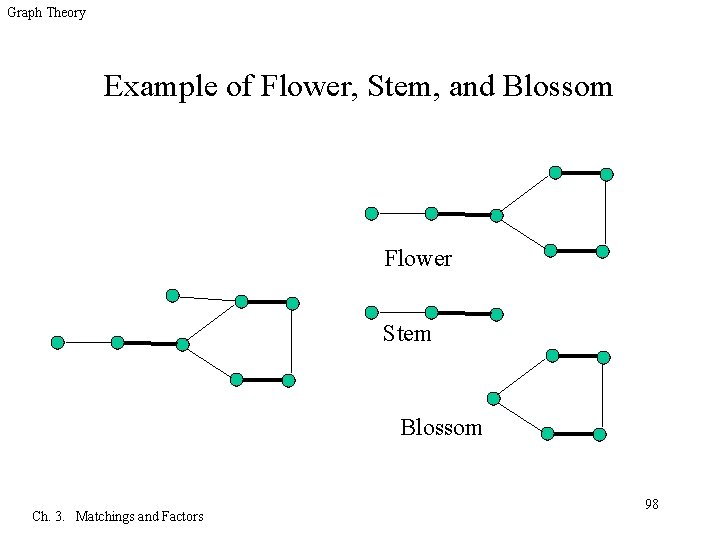
Graph Theory Flower, Stem, Blossom q That M be a matching in a graph G, and let u be an M-unsaturated vertex. – A flower is the union of two M-alternating paths from u that reach a vertex x on steps of opposite parity (having not done so earlier). – The stem of the flower is the maximal common initial path (of nonnegative even length). – The blossom of the flower is the odd cycle obtained by deleting the stem. Ch. 3. Matchings and Factors 97

Graph Theory Example of Flower, Stem, and Blossom Flower Stem Blossom Ch. 3. Matchings and Factors 98

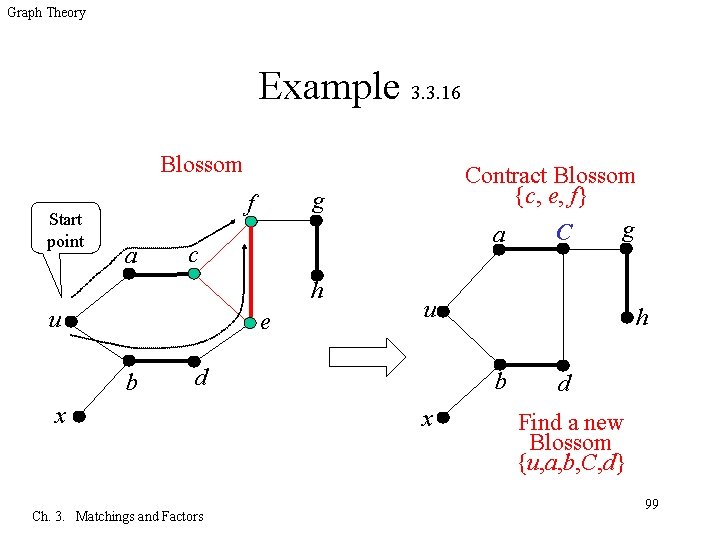
Graph Theory Example 3. 3. 16 Blossom Start point g f a c h u e b Contract Blossom {c, e, f} g C a u d x Ch. 3. Matchings and Factors h b x d Find a new Blossom {u, a, b, C, d} 99

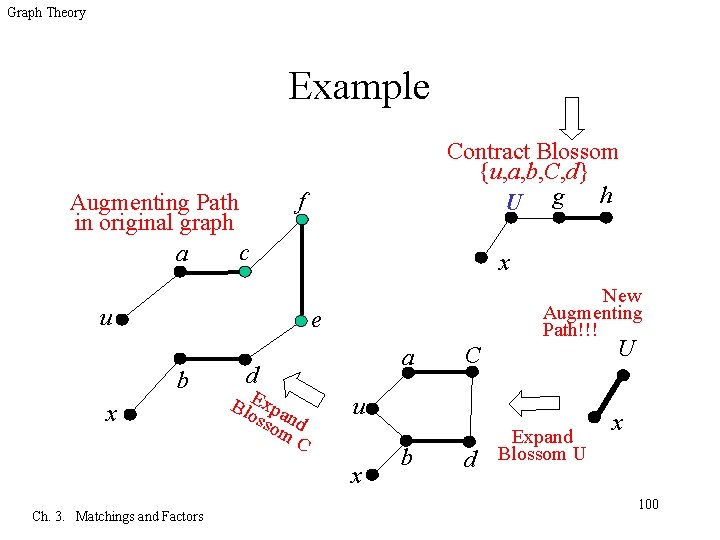
Graph Theory Example Augmenting Path in original graph c a Contract Blossom {u, a, b, C, d} h U g f u x New Augmenting Path!!! e b x a d Blo. Expa sso nd m C u x Ch. 3. Matchings and Factors U C b d Expand Blossom U x 100

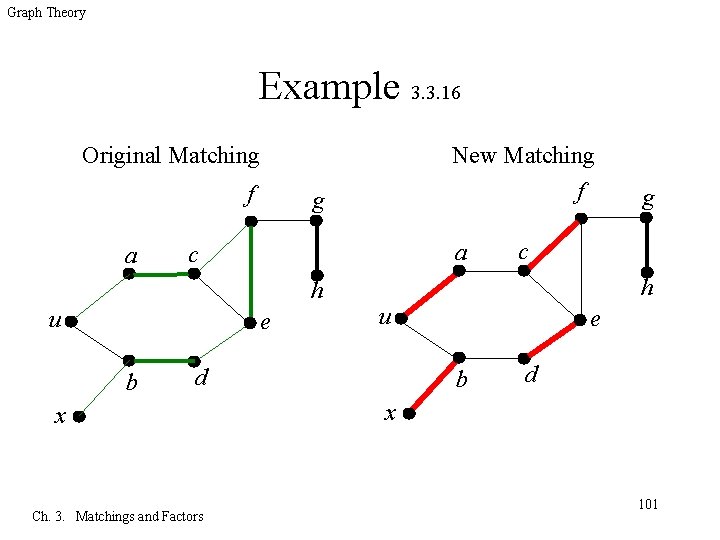
Graph Theory Example 3. 3. 16 Original Matching f a New Matching a c h u e b f g Ch. 3. Matchings and Factors c h u d x g e b d x 101

Graph Theory Edmonds’ Blossom Algorithm 3. 3. 17 Input: q A graph G, a matching M in G, an M-unsaturated vertex u. Ch. 3. Matchings and Factors 102

Graph Theory Edmonds’ Blossom Algorithm 3. 3. 17 Idea: q Explore M-altenating paths from u, recording for each vertex the vertex from which it was reached q Contract blossoms when found – Maintain sets S and T analogous to those in Algorithm 3. 2. 1, with S consisting of u and the vertices reached along saturated edges. q Reach an unsaturated vertex yields an augmentation Ch. 3. Matchings and Factors 103

Graph Theory Edmonds’ Blossom Algorithm 3. 3. 17 Initialization: q S={u} and T= Ch. 3. Matchings and Factors 104

Graph Theory Edmonds’ Blossom Algorithm 3. 3. 17 Iteration: step 1 q If S has no unmarked vertex, stop – There is no M-augmenting path from u q Otherwise, select an unmarked v S. To explore from v, successively consider each y N(v) such that y T. Ch. 3. Matchings and Factors 105

Graph Theory Edmonds’ Blossom Algorithm 3. 3. 17 Iteration: step 2 q If y is unsaturdated by M, then trace back from y (expanding blossoms as needed) to report an M-augmrnting u, y-path. Ch. 3. Matchings and Factors 106

Graph Theory Edmonds’ Blossom Algorithm 3. 3. 17 Iteration: step 3 q If y S, then a blossom has been found. – Suspend the exploration of v and contract the blossom, replacing its vertices in S and T by a single new vertex in S. – Continue the search from this vertex in the smaller graph. Otherwise, y is matched to some w by M. – Include y in T (reached from v), and include w in S (reached from y). Ch. 3. Matchings and Factors 107

Graph Theory Edmonds’ Blossom Algorithm 3. 3. 17 Iteration: step 4 q After exploring all such neighbors of v, mark v and iterate. Ch. 3. Matchings and Factors 108