Graph Theory Chapter 2 Basic Concepts in Graph

Graph Theory Chapter 2 Basic Concepts in Graph Theory 大葉大學 資訊 程系 黃鈴玲 2011. 9

Contents Ø Ø Ø Ø 2. 1 Paths and Cycles 2. 2 Connectivity 2. 3 Homomorphisms and Isomorphisms of Graphs 2. 4 More on Isomorphisms on Simple Graphs 2. 5 Formations and Minors of Graphs 2. 6 Homomorphisms and Isomorphisms for Digraphs 2. 7 Digraph Connectivity 2

2. 1 Paths and Cycles 3

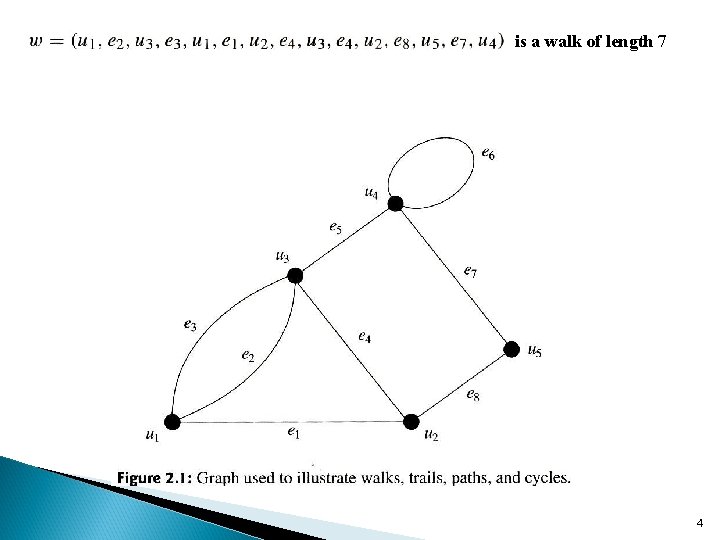
is a walk of length 7 4

5

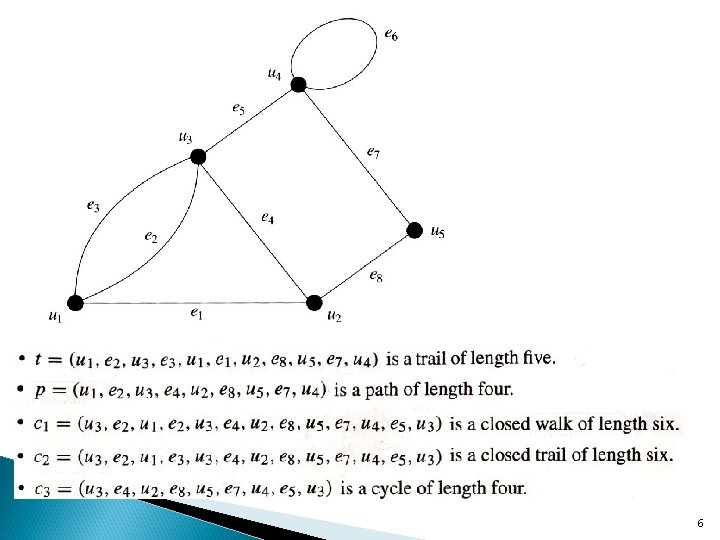
6

7

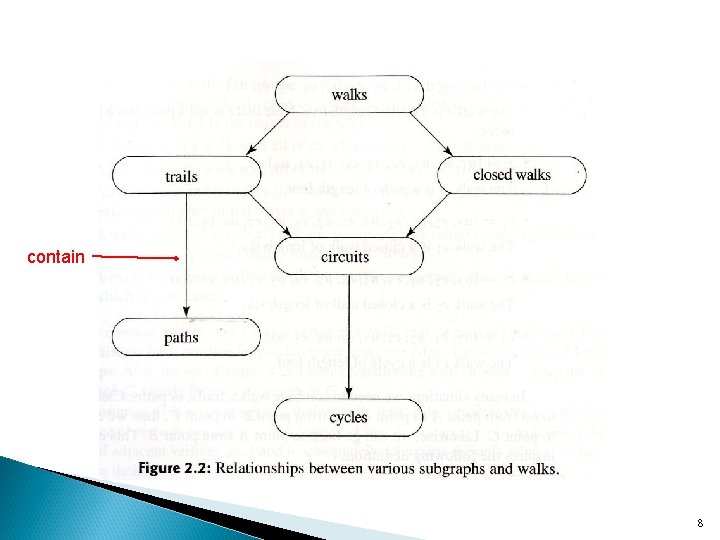
contain 8

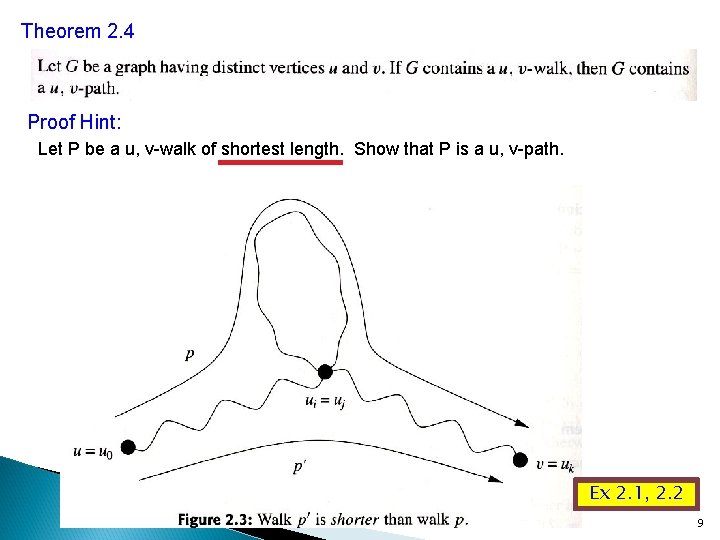
Theorem 2. 4 Proof Hint: Let P be a u, v-walk of shortest length. Show that P is a u, v-path. Ex 2. 1, 2. 2 9

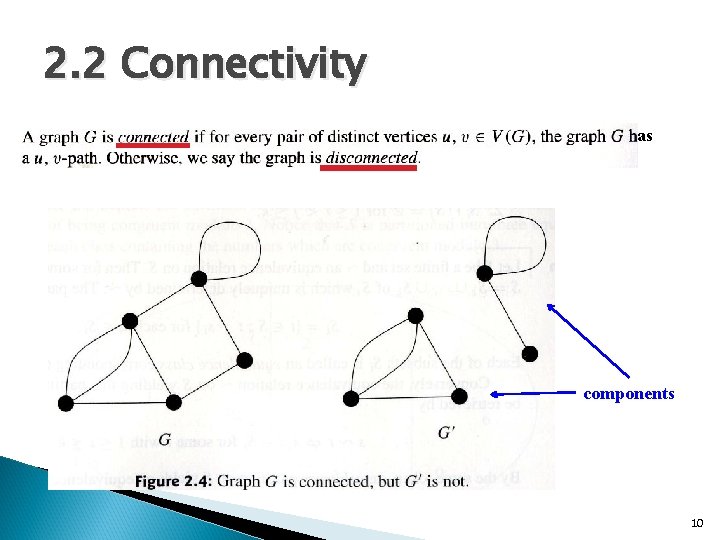
2. 2 Connectivity as components 10

Theorem 2. 13 For a simple graph G with n vertices and k components we have Proof Let H 1, H 2, …, Hk be the k components of G, and |V(Hi)| = ni for each i. By Lemma 2. 14, Ex 2. 4, 2. 5 11

2. 3 Homomorphisms and Isomorphisms of Graphs 當 f 是 G G’的 homomorphism時， 若u, v兩點在G中相連，則這兩點對應過去的 f(u)與f(v)也在G’中相連 12

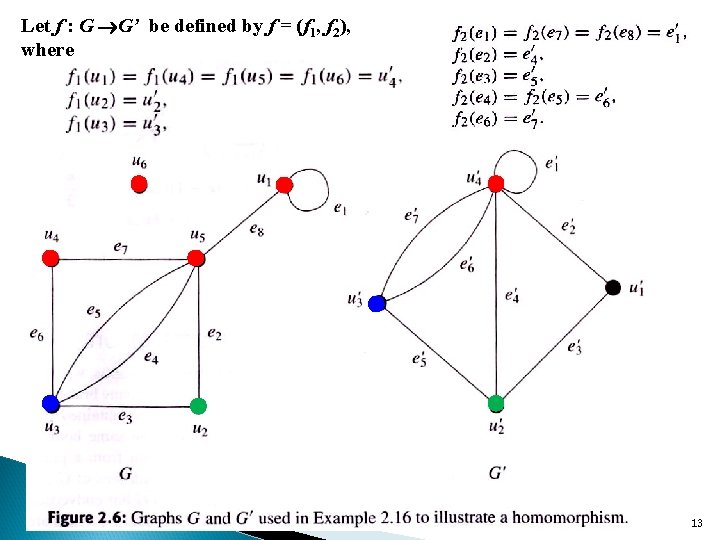
Let f : G G’ be defined by f = (f 1, f 2), where 13

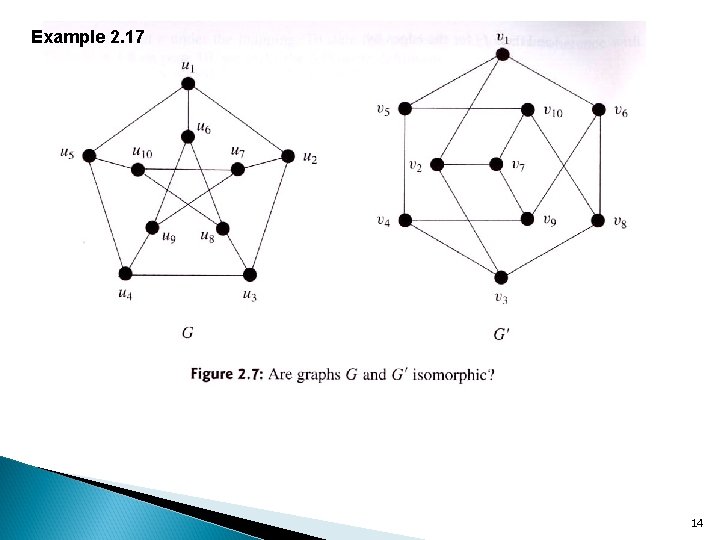
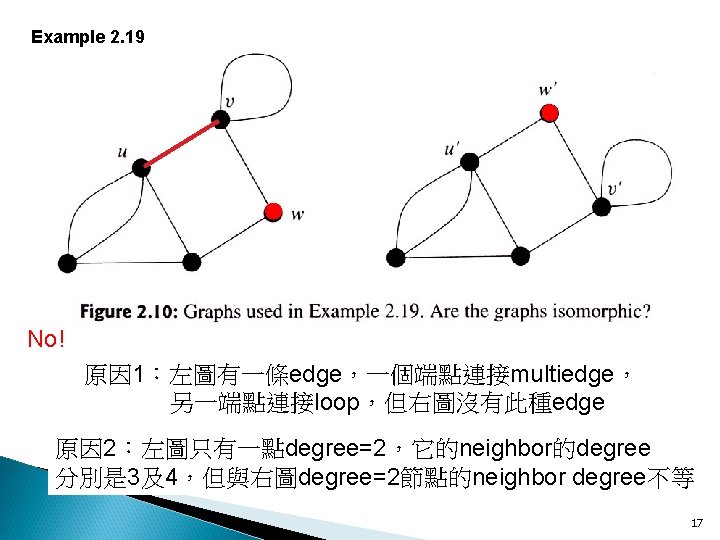
Example 2. 17 14

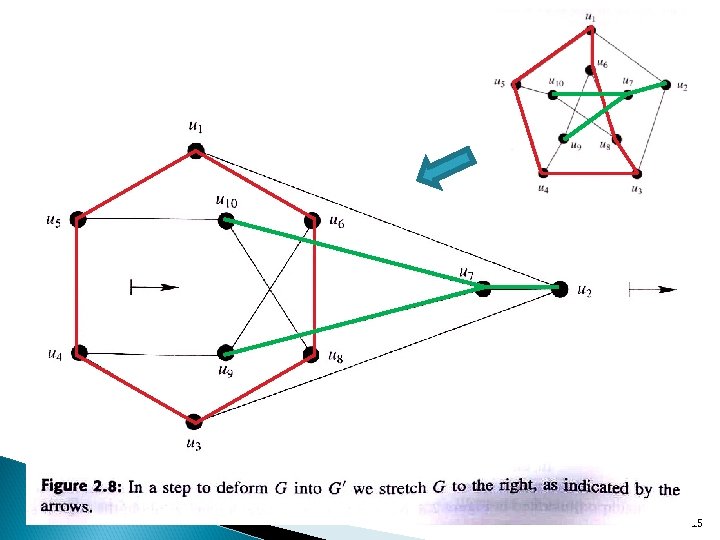
15

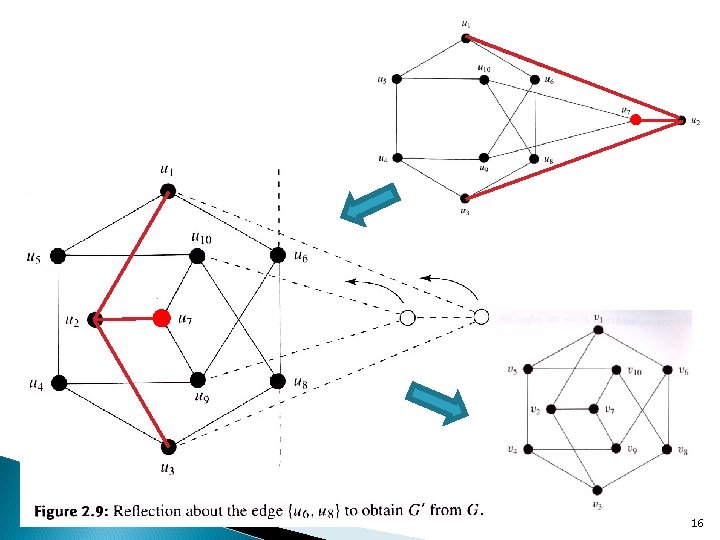
16

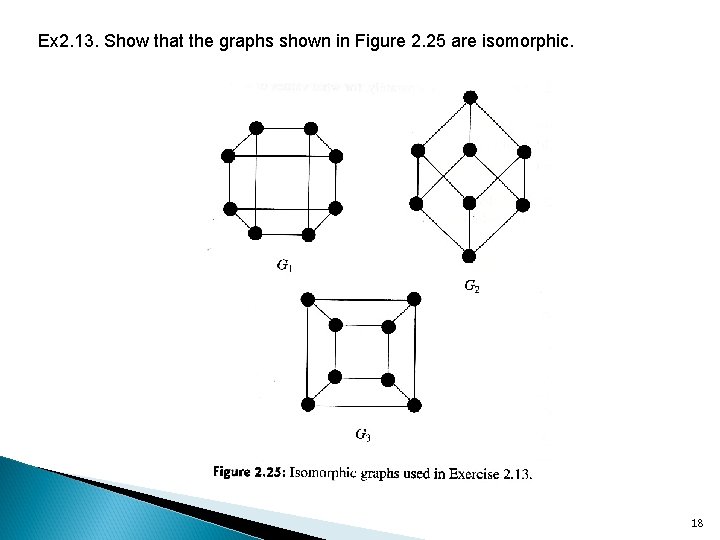
Ex 2. 13. Show that the graphs shown in Figure 2. 25 are isomorphic. 18

2. 4 More on Isomorphisms on Simple Graphs Observation 2. 22 Def 2. 24 Theorem 2. 25 Ex 2. 22, 2. 23 19

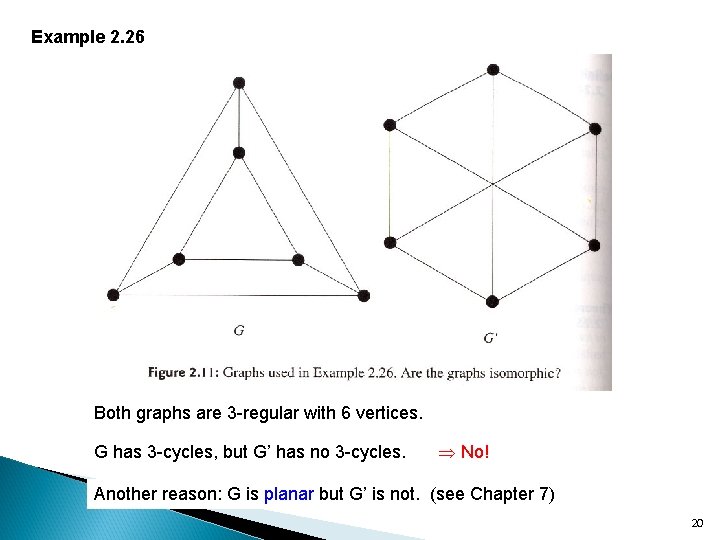
Example 2. 26 Both graphs are 3 -regular with 6 vertices. G has 3 -cycles, but G’ has no 3 -cycles. No! Another reason: G is planar but G’ is not. (see Chapter 7) 20

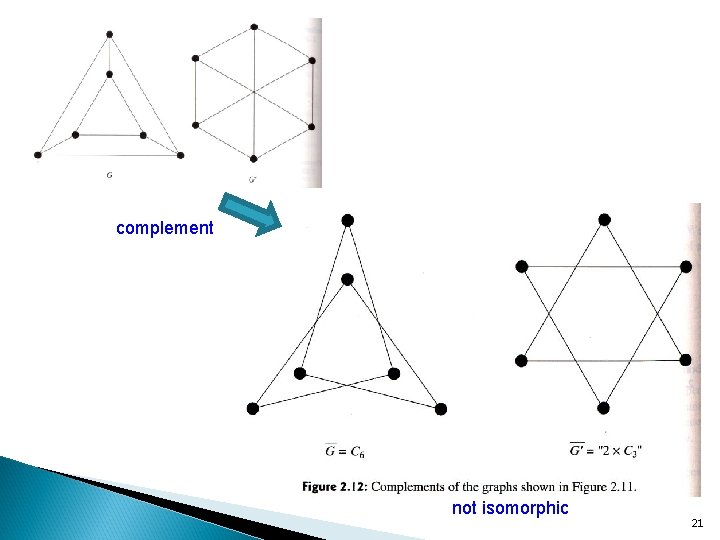
complement not isomorphic 21

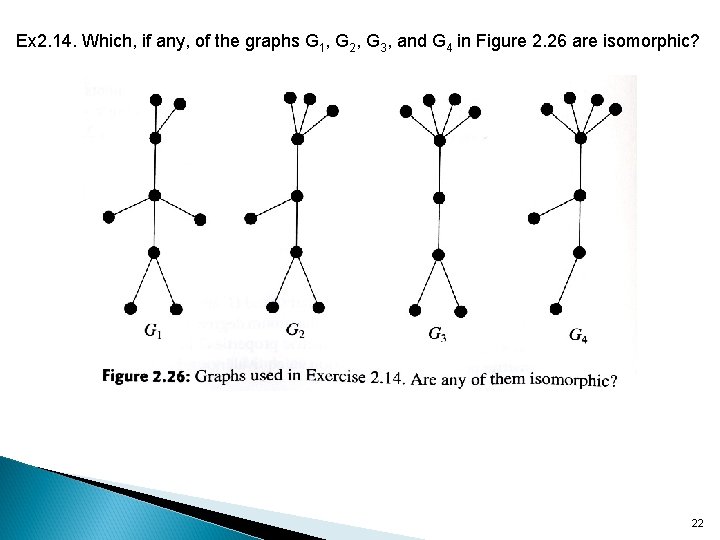
Ex 2. 14. Which, if any, of the graphs G 1, G 2, G 3, and G 4 in Figure 2. 26 are isomorphic? 22

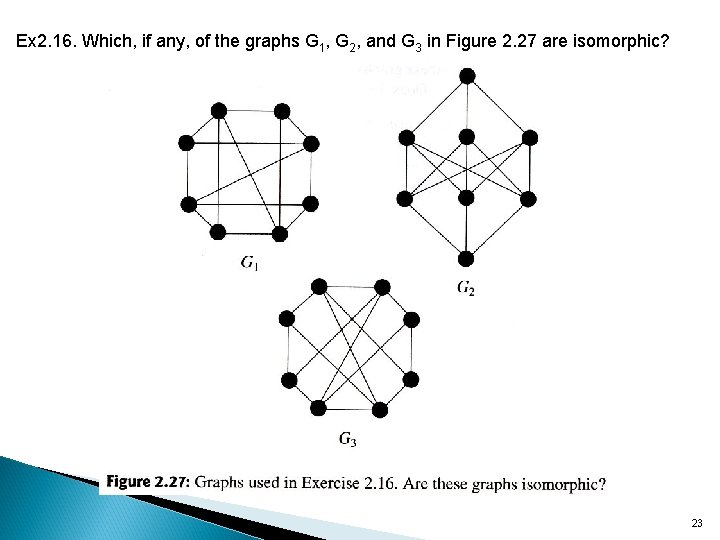
Ex 2. 16. Which, if any, of the graphs G 1, G 2, and G 3 in Figure 2. 27 are isomorphic? 23

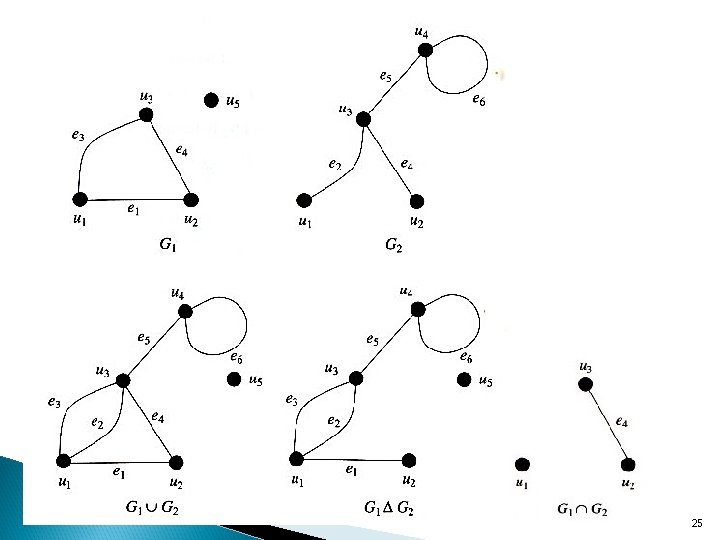
2. 5 Formations and Minors of Graphs Def 2. 27 24

25

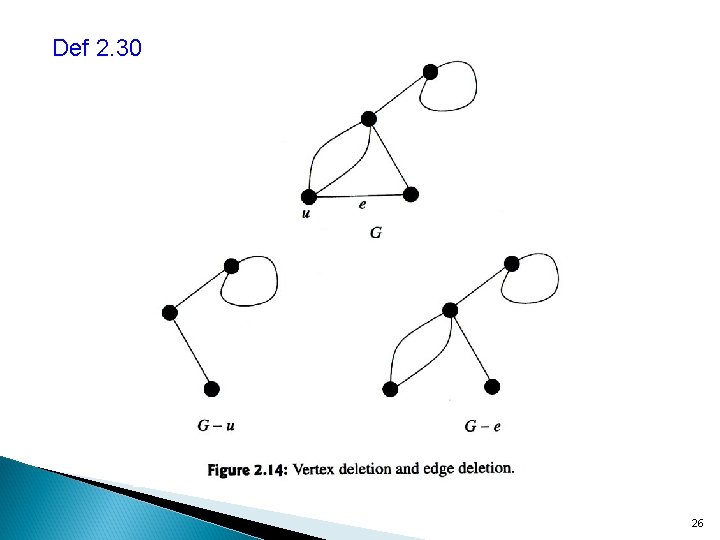
Def 2. 30 26

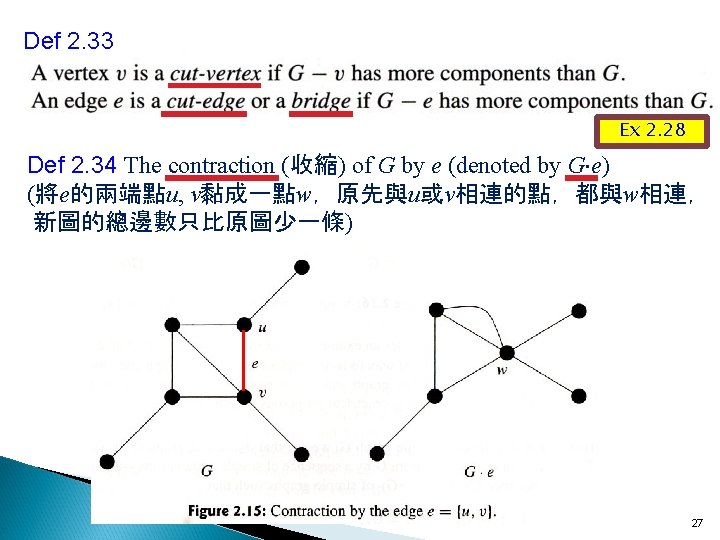
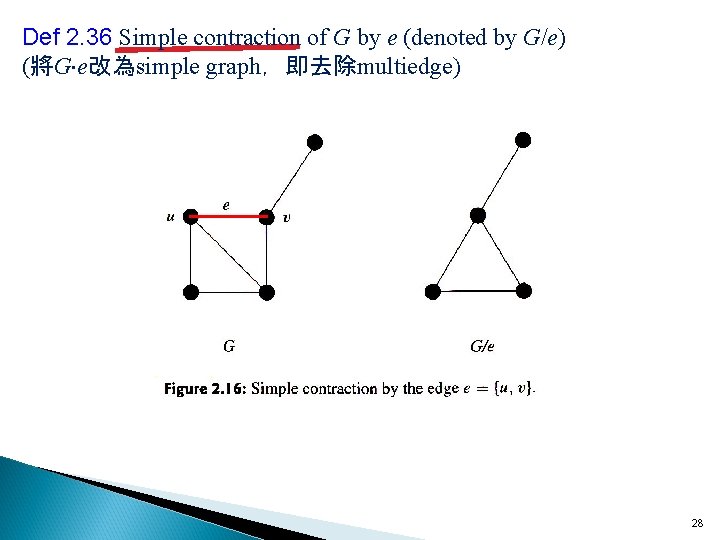
Def 2. 36 Simple contraction of G by e (denoted by G/e) (將G e改為simple graph，即去除multiedge) 28

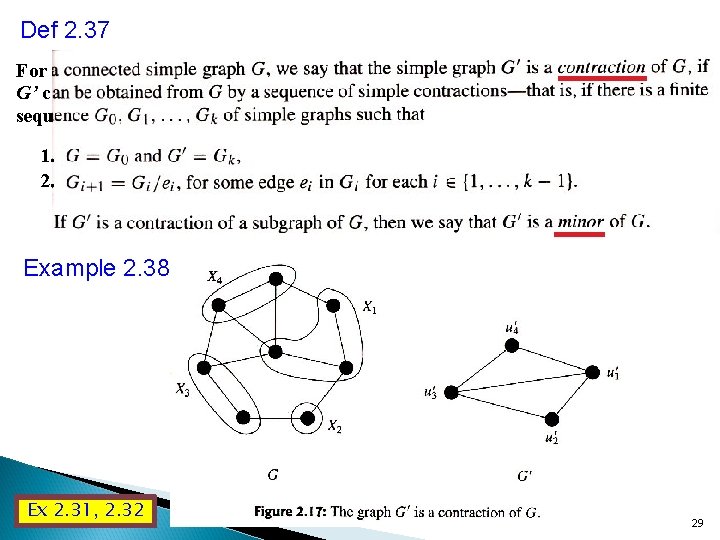
Def 2. 37 For G’ c sequ 1. 2. Example 2. 38 Ex 2. 31, 2. 32 29

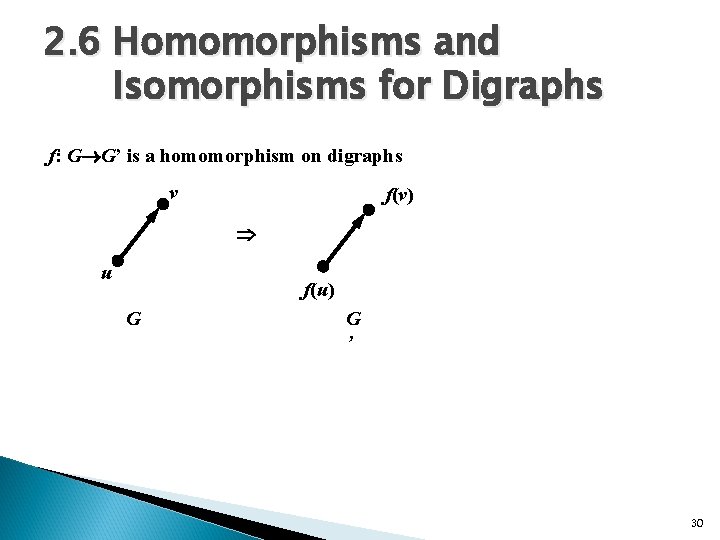
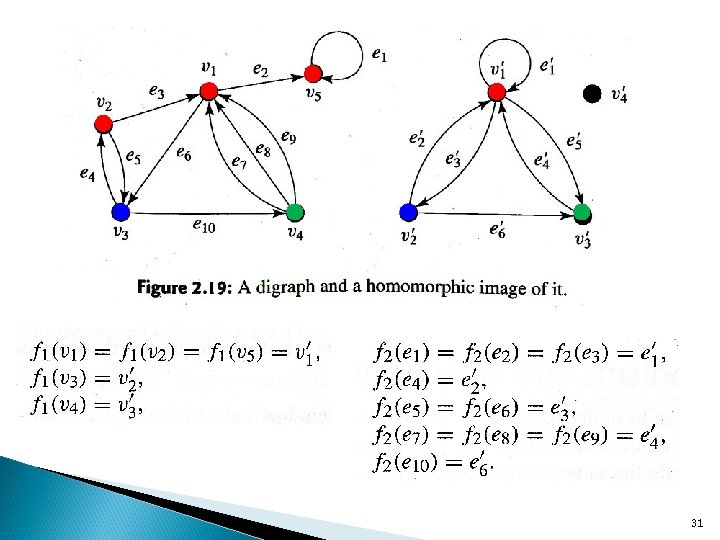
2. 6 Homomorphisms and Isomorphisms for Digraphs f: G G’ is a homomorphism on digraphs v f(v) u f(u) G G ’ 30

31

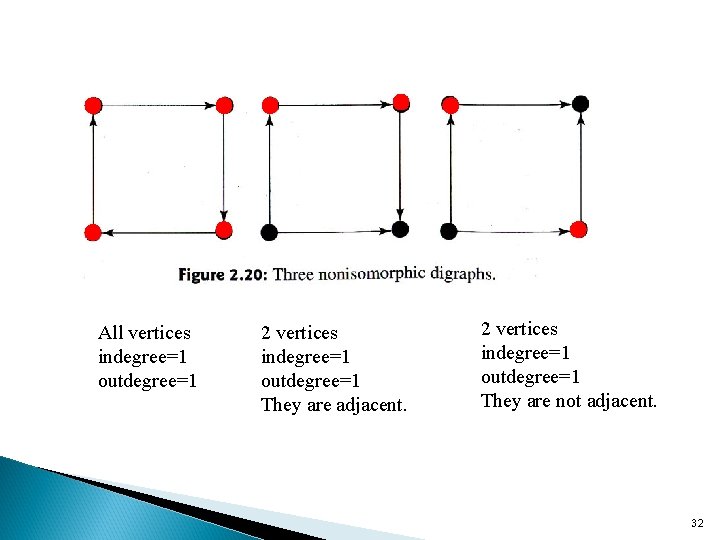
All vertices indegree=1 outdegree=1 2 vertices indegree=1 outdegree=1 They are adjacent. 2 vertices indegree=1 outdegree=1 They are not adjacent. 32

2. 7 Digraph Connectivity Def 2. 44 33

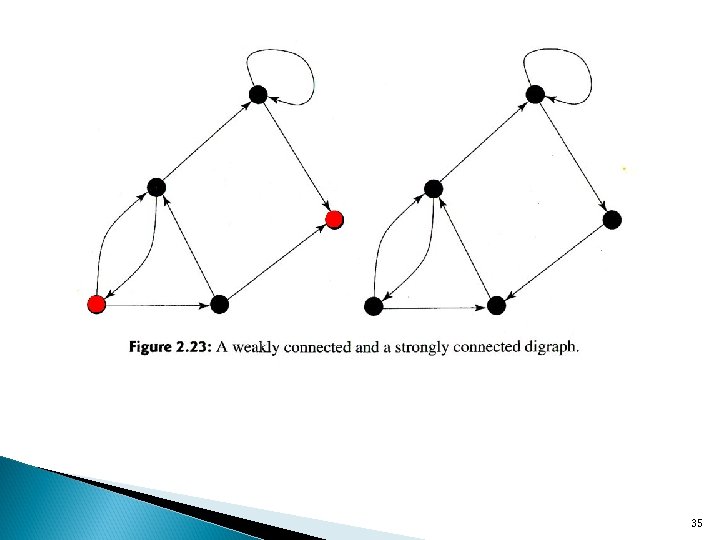
A digraph is called weakly connected if its underlying graph is connected. Def 2. 47 These two directed paths are not necessarily edge disjoint. 34

35

Example 2. 50 36

補充題: Show that there is no tournament on 6 vertices all of whose vertices have the same outdegree. 37