Graph Theory Basics for Social Network Theory John

Graph Theory Basics for Social Network Theory John G. Del Greco November 6, 2009

Introduction Graphs (networks) can be used to model an interaction structure among nodes (persons, firms, etc. ). Many different types of Interactions are possible: • Information exchange (bidirectional) or transmission (unidirectional) • WWW links • Trade • Credit and financial flows • Trust Social • Friendship network • Spread of diseases theory • Diffusion of ideas or attitudes through a population • Etc!

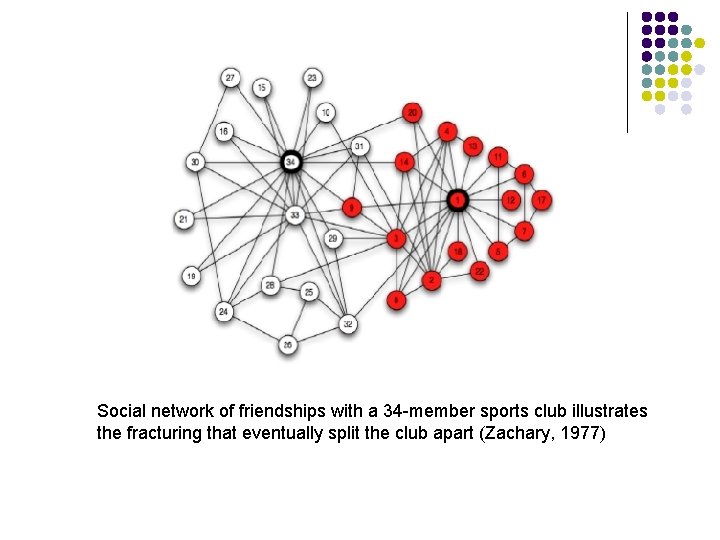
Social network of friendships with a 34 -member sports club illustrates the fracturing that eventually split the club apart (Zachary, 1977)

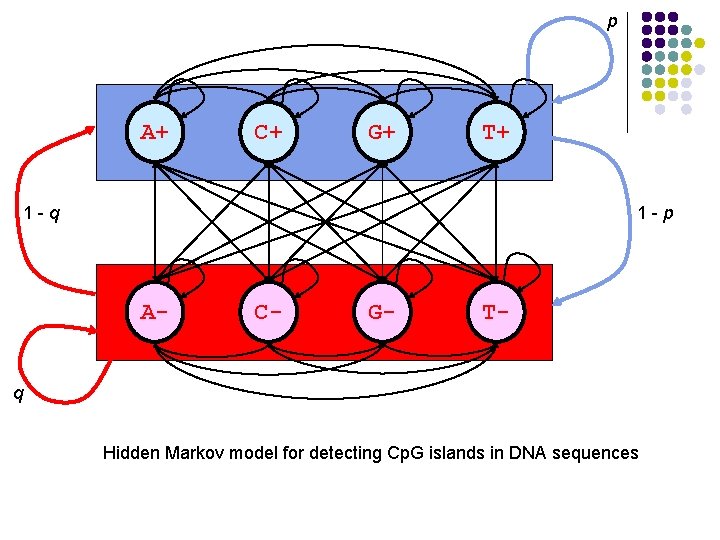
p A+ C+ G+ T+ 1 -q 1 -p A- C- G- T- q Hidden Markov model for detecting Cp. G islands in DNA sequences

Overview Graphs • Size and order • Representations • Degree and degree distributions • Subgraphs • Paths and components • Shortest paths (geodesics) • Special graphs • Vertex centrality measures Directed Graphs • Dyad and triad census • Paths, semipaths, geodesics, weak and strong components • Centrality for directed graphs • Special directed graphs

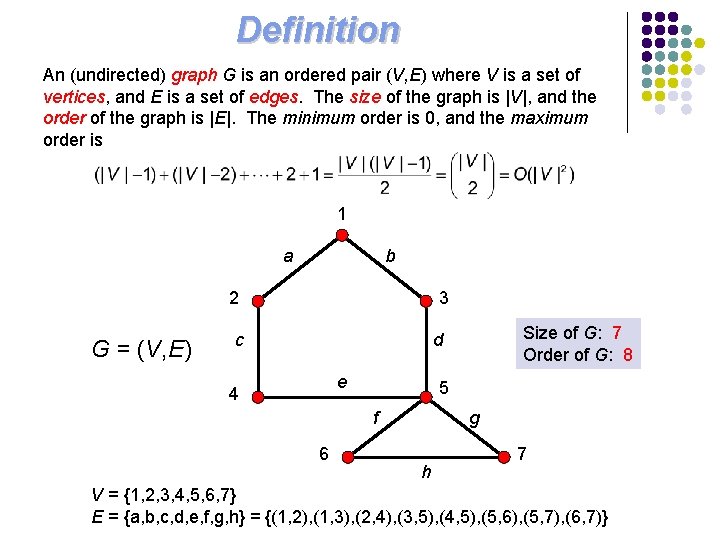
Definition An (undirected) graph G is an ordered pair (V, E) where V is a set of vertices, and E is a set of edges. The size of the graph is |V|, and the order of the graph is |E|. The minimum order is 0, and the maximum order is 1 a b 2 G = (V, E) 3 c Size of G: 7 Order of G: 8 d e 4 5 f 6 g h 7 V = {1, 2, 3, 4, 5, 6, 7} E = {a, b, c, d, e, f, g, h} = {(1, 2), (1, 3), (2, 4), (3, 5), (4, 5), (5, 6), (5, 7), (6, 7)}

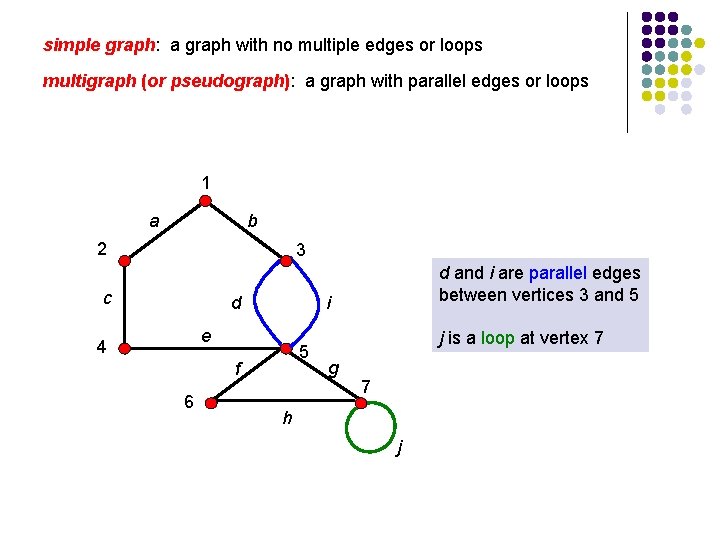
simple graph: a graph with no multiple edges or loops multigraph (or pseudograph): a graph with parallel edges or loops 1 a b 2 3 c d i e 4 5 f 6 d and i are parallel edges between vertices 3 and 5 j is a loop at vertex 7 g 7 h j

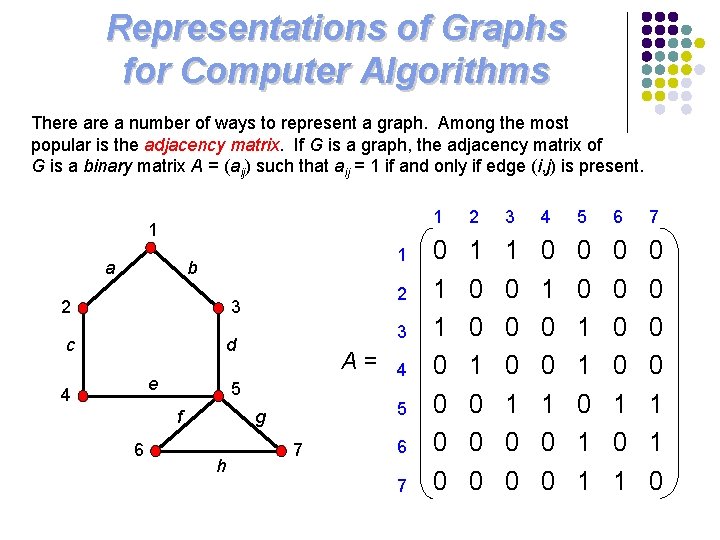
Representations of Graphs for Computer Algorithms There a number of ways to represent a graph. Among the most popular is the adjacency matrix. If G is a graph, the adjacency matrix of G is a binary matrix A = (aij) such that aij = 1 if and only if edge (i, j) is present. 1 a 1 b 2 3 c d e 4 3 A= 5 f 6 2 5 g h 4 7 6 7 1 2 3 4 5 6 7 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 0

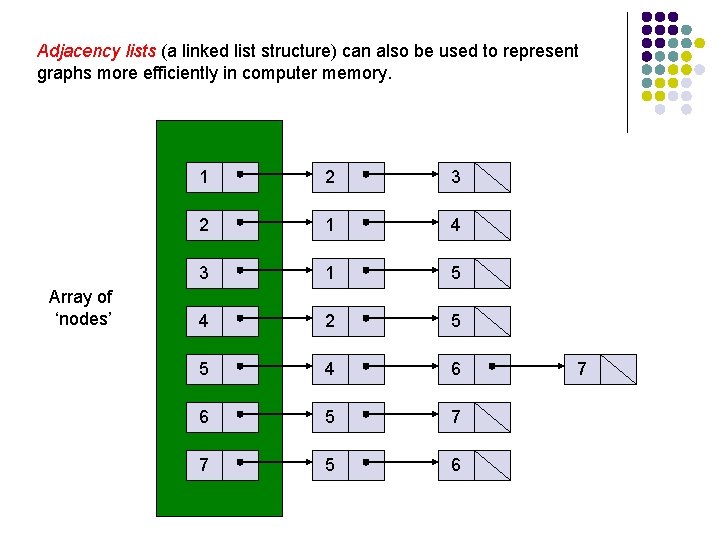
Adjacency lists (a linked list structure) can also be used to represent graphs more efficiently in computer memory. Array of ‘nodes’ 1 2 3 2 1 4 3 1 5 4 2 5 5 4 6 6 5 7 7 5 6 7

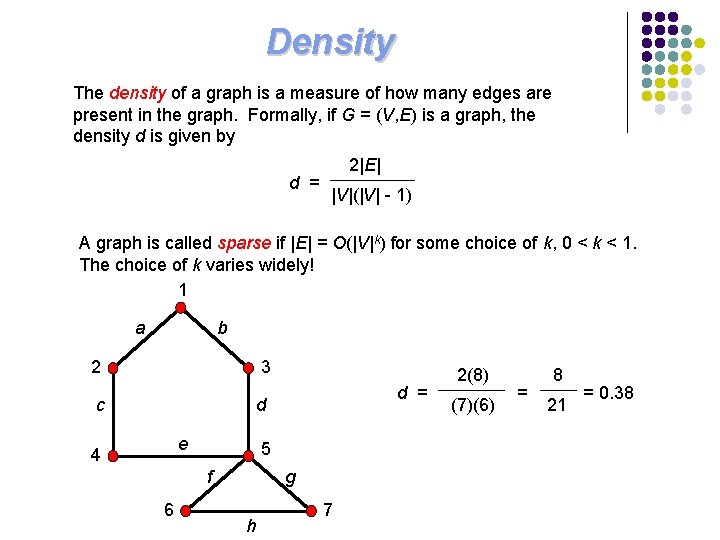
Density The density of a graph is a measure of how many edges are present in the graph. Formally, if G = (V, E) is a graph, the density d is given by d = 2|E| |V|(|V| - 1) A graph is called sparse if |E| = O(|V|k) for some choice of k, 0 < k < 1. The choice of k varies widely! 1 a b 2 3 c d e 4 5 f 6 d = g h 7 2(8) (7)(6) = 8 21 = 0. 38

d=1 Complete graph K 5 d=0 Empty graph

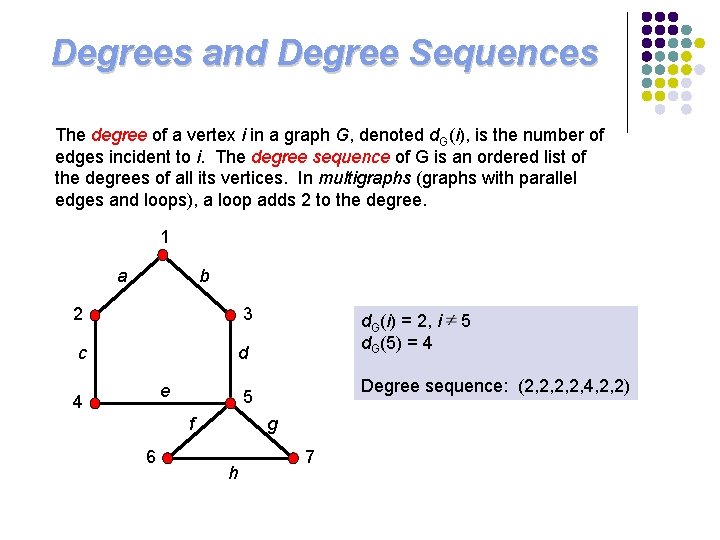
Degrees and Degree Sequences The degree of a vertex i in a graph G, denoted d. G(i), is the number of edges incident to i. The degree sequence of G is an ordered list of the degrees of all its vertices. In multigraphs (graphs with parallel edges and loops), a loop adds 2 to the degree. 1 a b 2 3 c d e 4 g h 5 Degree sequence: (2, 2, 4, 2, 2) 5 f 6 d. G(i) = 2, i d. G(5) = 4 7

graphical sequence: a sequence S = (d 1, d 2, . . . , dn) of non-negative integers such that S is the degree sequence of some graph Not every sequence is graphical! Consider S = (1, 1, 1). Question When is a sequence of nonnegative integers the degree sequence of some graph? Multigraph: answer is easy! Simple graph: answer is a litte harder!

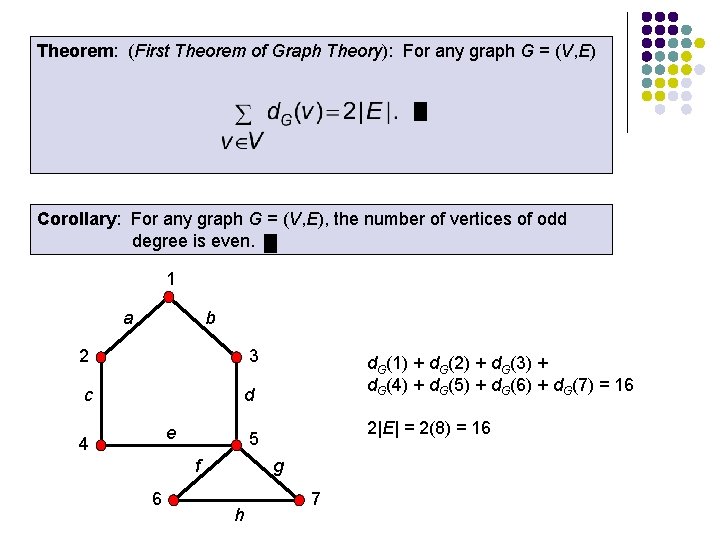
Theorem: (First Theorem of Graph Theory): For any graph G = (V, E) Corollary: For any graph G = (V, E), the number of vertices of odd degree is even. 1 a b 2 3 c d e 4 2|E| = 2(8) = 16 5 f 6 d. G(1) + d. G(2) + d. G(3) + d. G(4) + d. G(5) + d. G(6) + d. G(7) = 16 g h 7

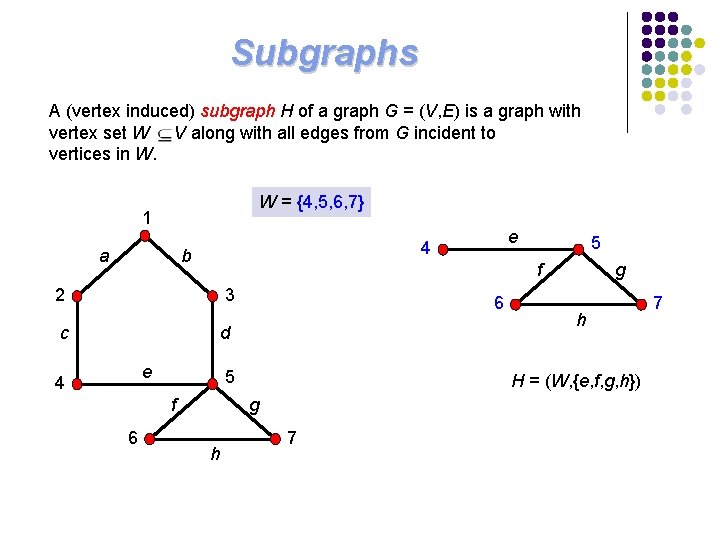
Subgraphs A (vertex induced) subgraph H of a graph G = (V, E) is a graph with vertex set W V along with all edges from G incident to vertices in W. W = {4, 5, 6, 7} 1 a b 3 c d e 6 5 f 2 4 e 4 h H = (W, {e, f, g, h}) g h g 7 7

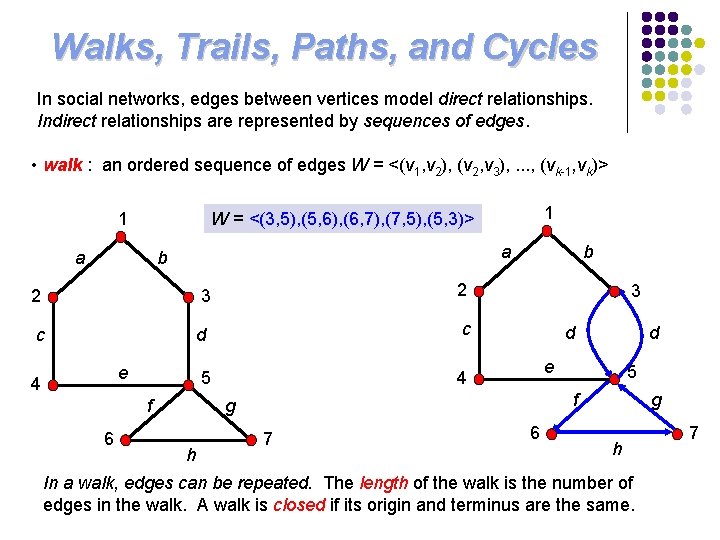
Walks, Trails, Paths, and Cycles In social networks, edges between vertices model direct relationships. Indirect relationships are represented by sequences of edges. • walk : an ordered sequence of edges W = <(v 1, v 2), (v 2, v 3), . . . , (vk-1, vk)> a a b 2 3 2 c d c 5 4 e 4 f 6 1 W = <(3, 5), (5, 6), (6, 7), (7, 5), (5, 3)> 1 b 3 d e 5 f g h d 7 6 g h In a walk, edges can be repeated. The length of the walk is the number of edges in the walk. A walk is closed if its origin and terminus are the same. 7

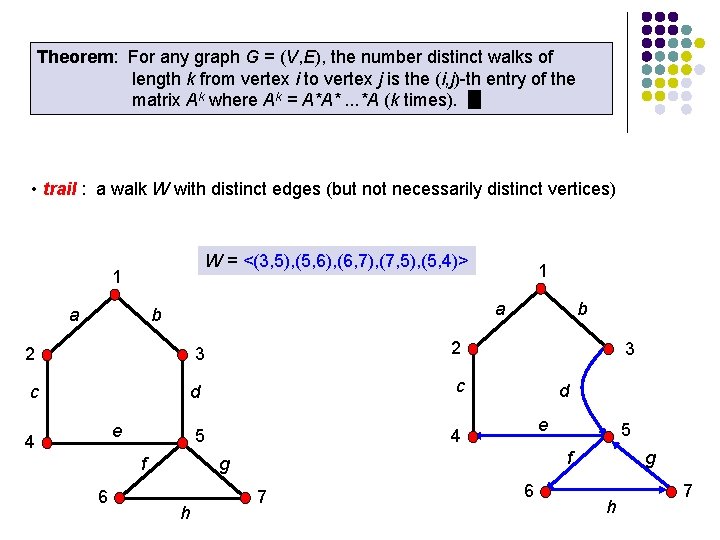
Theorem: For any graph G = (V, E), the number distinct walks of length k from vertex i to vertex j is the (i, j)-th entry of the matrix Ak where Ak = A*A*. . . *A (k times). • trail : a walk W with distinct edges (but not necessarily distinct vertices) W = <(3, 5), (5, 6), (6, 7), (7, 5), (5, 4)> 1 a a b 2 3 2 c d c 5 4 e 4 f 6 1 b 3 d e f g h 5 7 6 g h 7

. . Konigsberg Bridge Problem Starting on any bank, is it possible to cross all seven bridges exactly once and return to the starting bank?

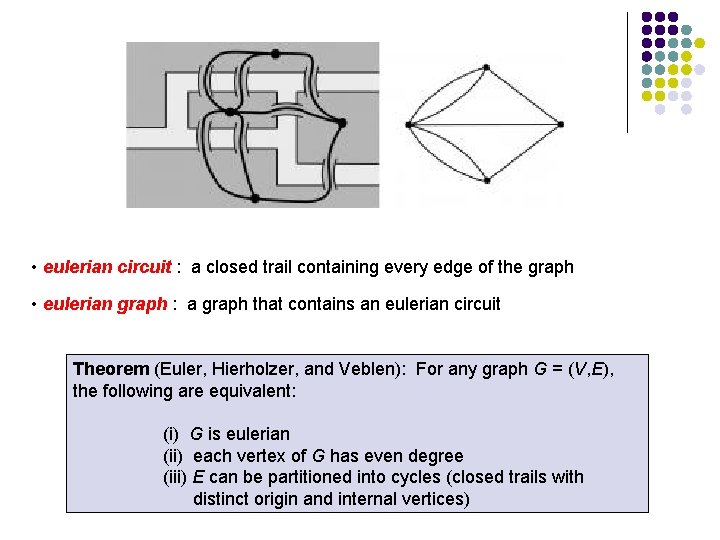
• eulerian circuit : a closed trail containing every edge of the graph • eulerian graph : a graph that contains an eulerian circuit Theorem (Euler, Hierholzer, and Veblen): For any graph G = (V, E), the following are equivalent: (i) G is eulerian (ii) each vertex of G has even degree (iii) E can be partitioned into cycles (closed trails with distinct origin and internal vertices)

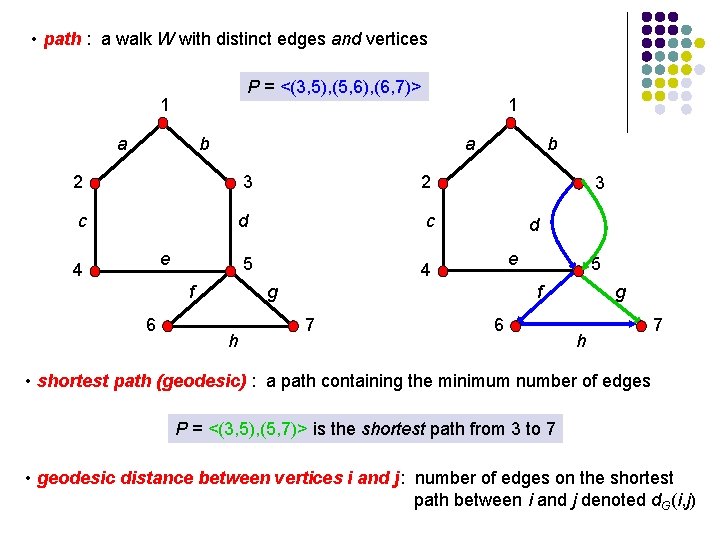
• path : a walk W with distinct edges and vertices P = <(3, 5), (5, 6), (6, 7)> 1 a b 2 3 2 c d c 5 4 e 4 f 6 b 3 d e g h 5 f 7 6 g h 7 • shortest path (geodesic) : a path containing the minimum number of edges P = <(3, 5), (5, 7)> is the shortest path from 3 to 7 • geodesic distance between vertices i and j: number of edges on the shortest path between i and j denoted d. G(i, j)

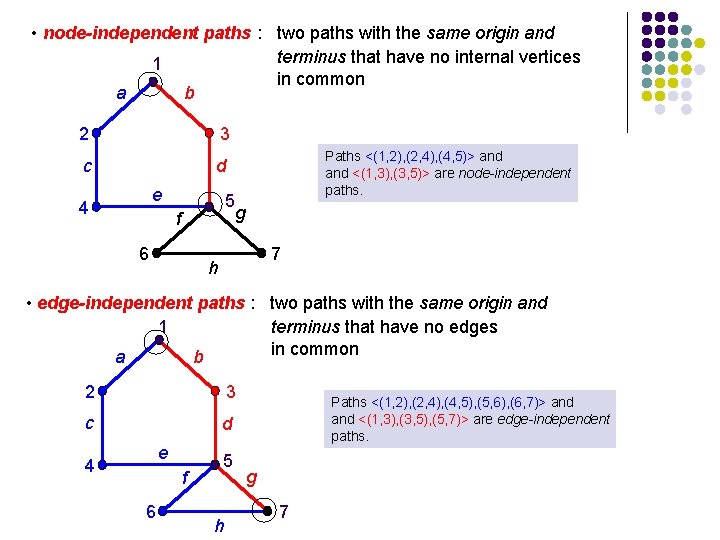
• node-independent paths : two paths with the same origin and terminus that have no internal vertices 1 in common a b 2 3 c d e 4 5 f 6 Paths <(1, 2), (2, 4), (4, 5)> and <(1, 3), (3, 5)> are node-independent paths. g 7 h • edge-independent paths : two paths with the same origin and terminus that have no edges 1 in common a b 2 3 c d e 4 f 6 5 h Paths <(1, 2), (2, 4), (4, 5), (5, 6), (6, 7)> and <(1, 3), (3, 5), (5, 7)> are edge-independent paths. g 7

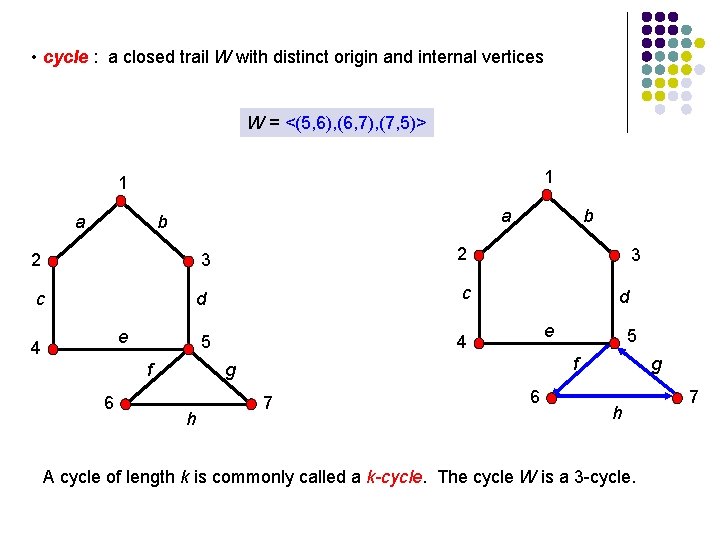
• cycle : a closed trail W with distinct origin and internal vertices W = <(5, 6), (6, 7), (7, 5)> 1 1 a a b 2 3 2 c d c 5 4 e 4 f 6 b 3 d e f g h 5 7 6 g h A cycle of length k is commonly called a k-cycle. The cycle W is a 3 -cycle. 7

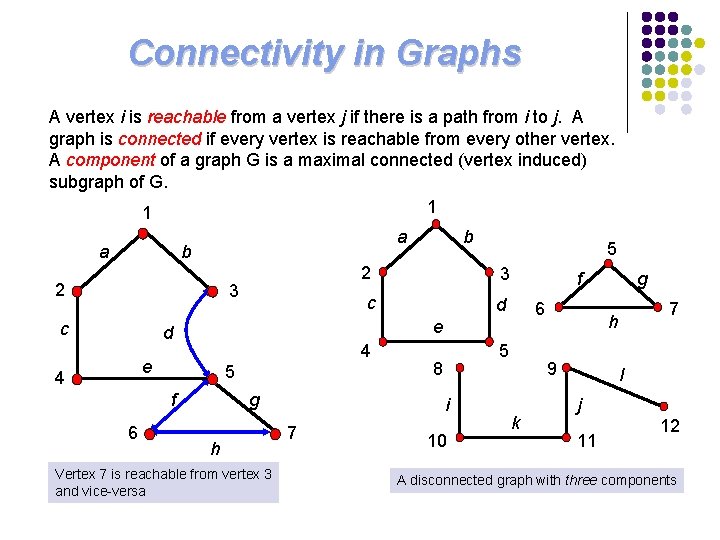
Connectivity in Graphs A vertex i is reachable from a vertex j if there is a path from i to j. A graph is connected if every vertex is reachable from every other vertex. A component of a graph G is a maximal connected (vertex induced) subgraph of G. 1 1 a a b 2 3 c d 4 e 5 f 6 e d 4 b g h Vertex 7 is reachable from vertex 3 and vice-versa 5 8 i 7 10 7 h 9 k g l j 11 12 A disconnected graph with three components

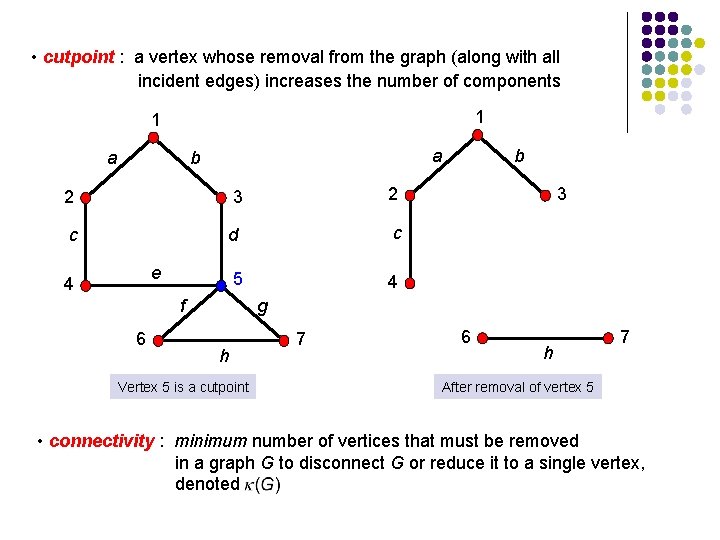
• cutpoint : a vertex whose removal from the graph (along with all incident edges) increases the number of components 1 1 a a b 2 3 2 c d c 5 4 e 4 f 6 b 3 g h Vertex 5 is a cutpoint 7 6 h 7 After removal of vertex 5 • connectivity : minimum number of vertices that must be removed in a graph G to disconnect G or reduce it to a single vertex, denoted

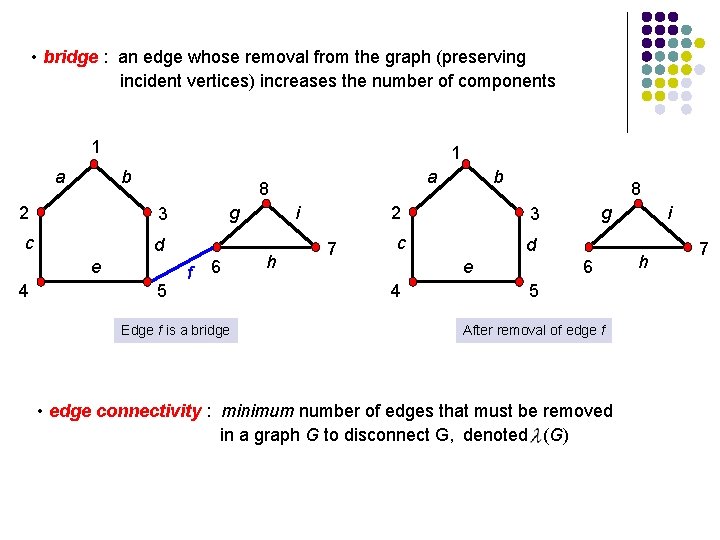
• bridge : an edge whose removal from the graph (preserving incident vertices) increases the number of components 1 a 1 b 2 3 c d e 4 a 8 5 g f 6 Edge f is a bridge i h 7 b 8 2 3 c d e 4 g 6 5 After removal of edge f • edge connectivity : minimum number of edges that must be removed in a graph G to disconnect G, denoted (G) i h 7

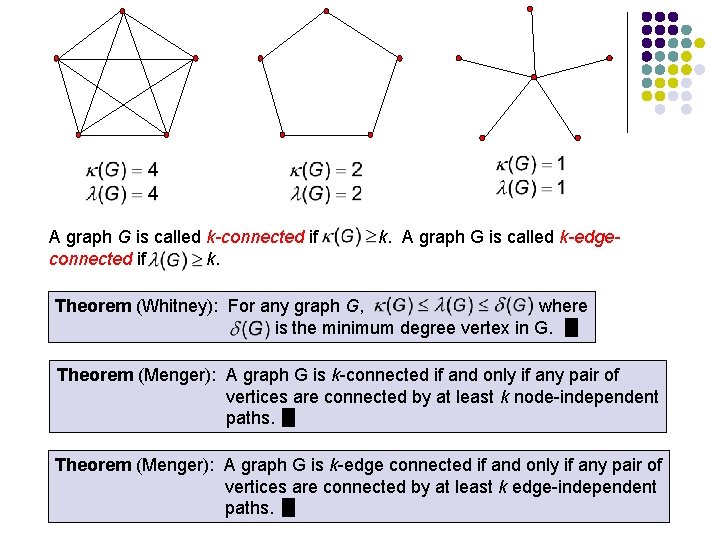
A graph G is called k-connected if k. k. A graph G is called k-edge- Theorem (Whitney): For any graph G, where is the minimum degree vertex in G. Theorem (Menger): A graph G is k-connected if and only if any pair of vertices are connected by at least k node-independent paths. Theorem (Menger): A graph G is k-edge connected if and only if any pair of vertices are connected by at least k edge-independent paths.

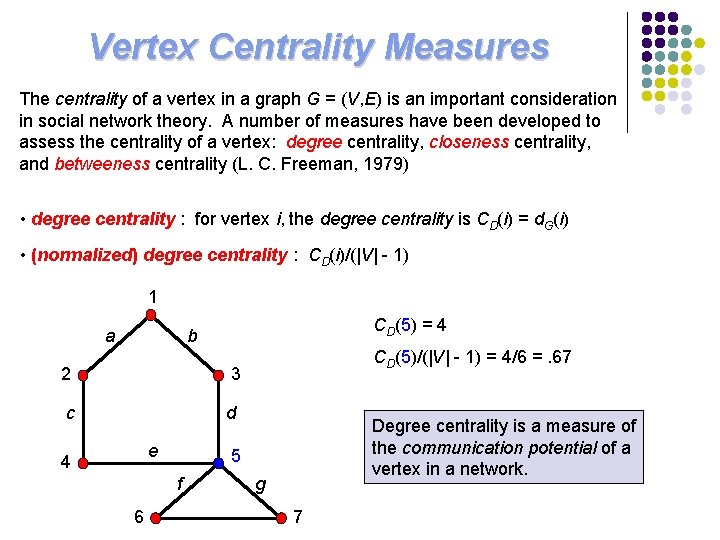
Vertex Centrality Measures The centrality of a vertex in a graph G = (V, E) is an important consideration in social network theory. A number of measures have been developed to assess the centrality of a vertex: degree centrality, closeness centrality, and betweeness centrality (L. C. Freeman, 1979) • degree centrality : for vertex i, the degree centrality is CD(i) = d. G(i) • (normalized) degree centrality : CD(i)/(|V| - 1) 1 a CD(5) = 4 b 2 3 c d e 4 Degree centrality is a measure of the communication potential of a vertex in a network. 5 f 6 CD(5)/(|V| - 1) = 4/6 =. 67 g 7

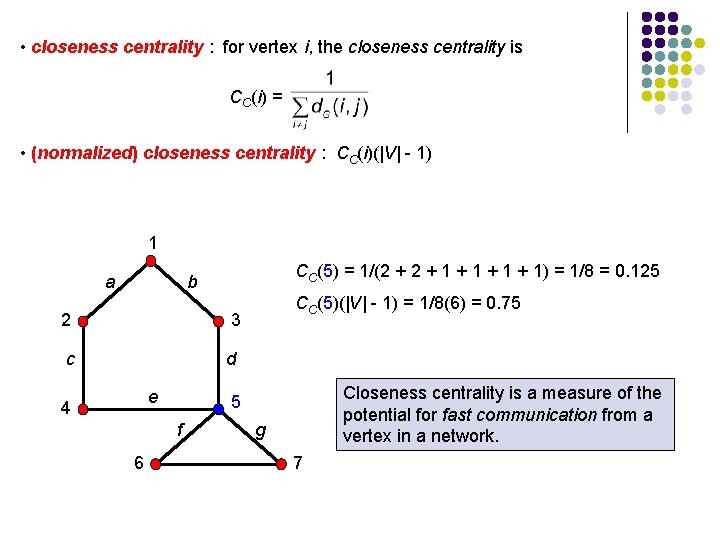
• closeness centrality : for vertex i, the closeness centrality is CC(i) = • (normalized) closeness centrality : CC(i)(|V| - 1) 1 a CC(5) = 1/(2 + 1 + 1 + 1) = 1/8 = 0. 125 b 2 3 c d e 4 Closeness centrality is a measure of the potential for fast communication from a vertex in a network. 5 f 6 CC(5)(|V| - 1) = 1/8(6) = 0. 75 g 7

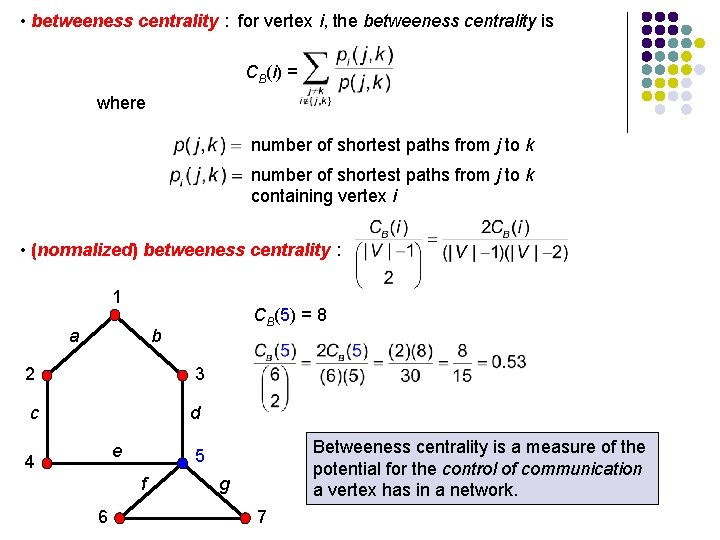
• betweeness centrality : for vertex i, the betweeness centrality is CB(i) = where number of shortest paths from j to k containing vertex i • (normalized) betweeness centrality : 1 a CB(5) = 8 b 2 3 c d e 4 f 6 Betweeness centrality is a measure of the potential for the control of communication a vertex has in a network. 5 g 7

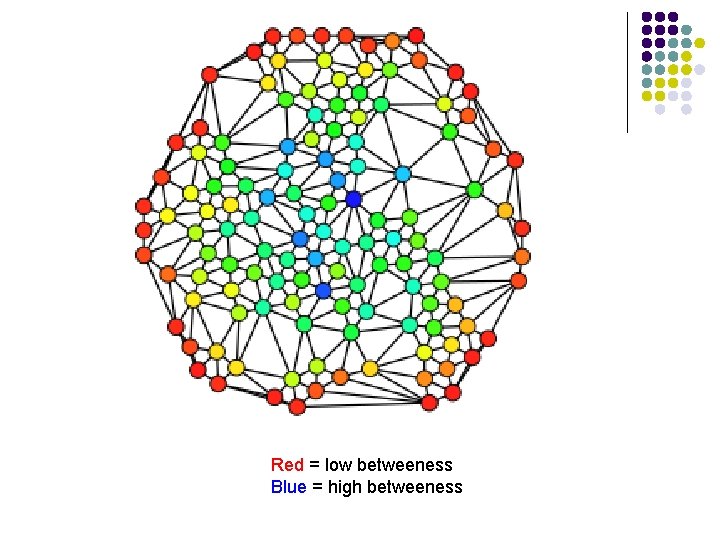
Red = low betweeness Blue = high betweeness

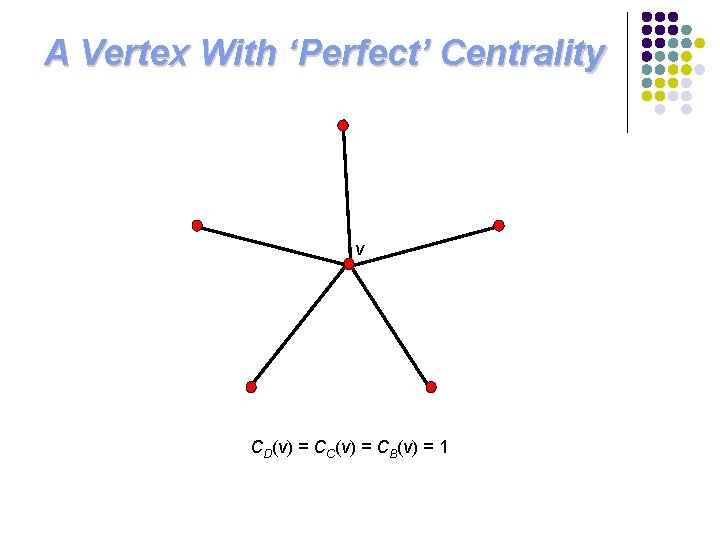
A Vertex With ‘Perfect’ Centrality v CD(v) = CC(v) = CB(v) = 1

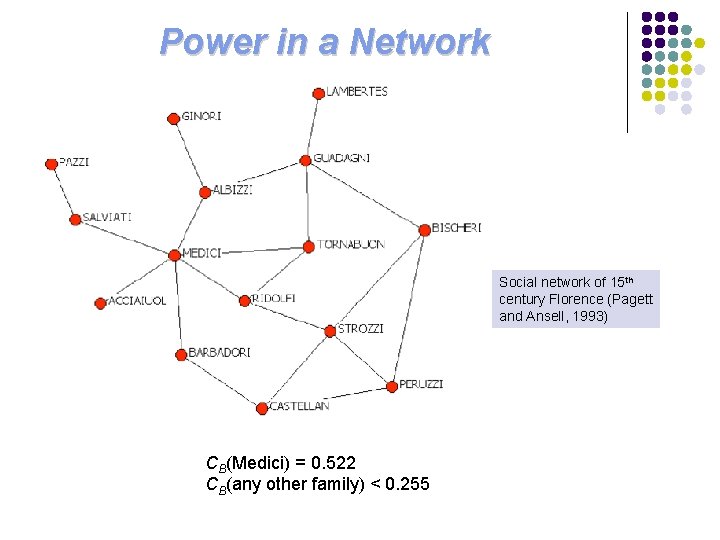
Power in a Network Social network of 15 th century Florence (Pagett and Ansell, 1993) CB(Medici) = 0. 522 CB(any other family) < 0. 255