Graph Theory as it Relates to Sports Scheduling

Graph Theory as it Relates to Sports Scheduling By: Kelly Kinder

Overview Terminology of Graph Theory n How Graph Theory Relates to Scheduling n How I used Graph Theory to Create a Schedule for the National Basketball Association n

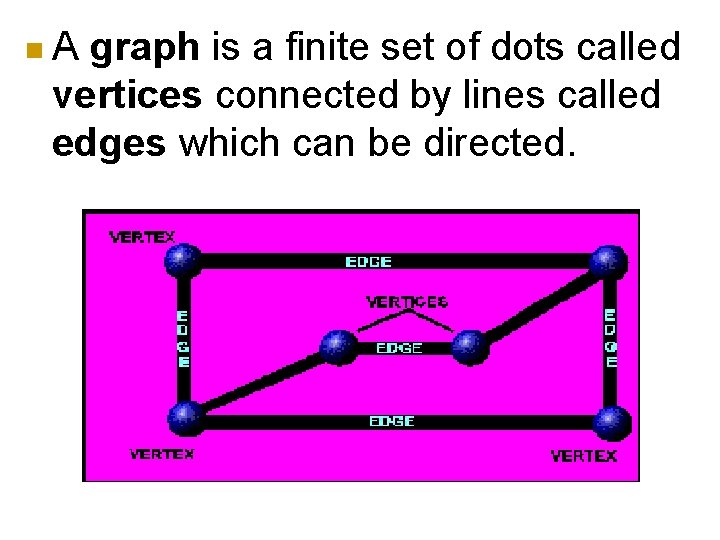
n. A graph is a finite set of dots called vertices connected by lines called edges which can be directed.

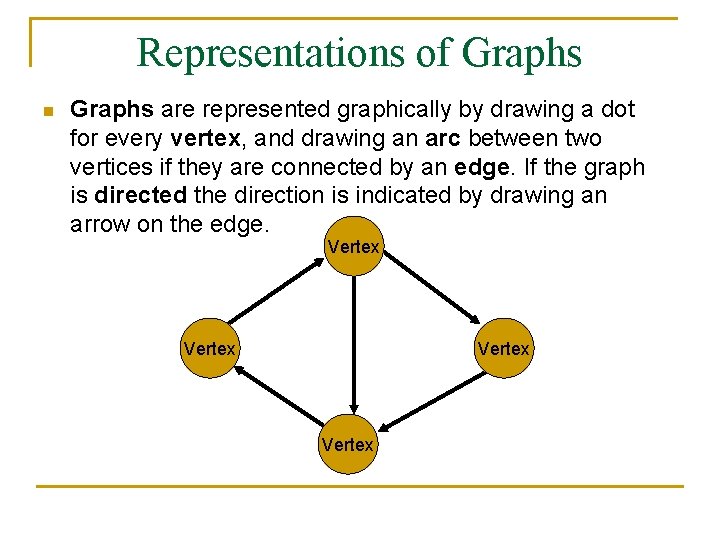
Representations of Graphs n Graphs are represented graphically by drawing a dot for every vertex, and drawing an arc between two vertices if they are connected by an edge. If the graph is directed the direction is indicated by drawing an arrow on the edge. Vertex

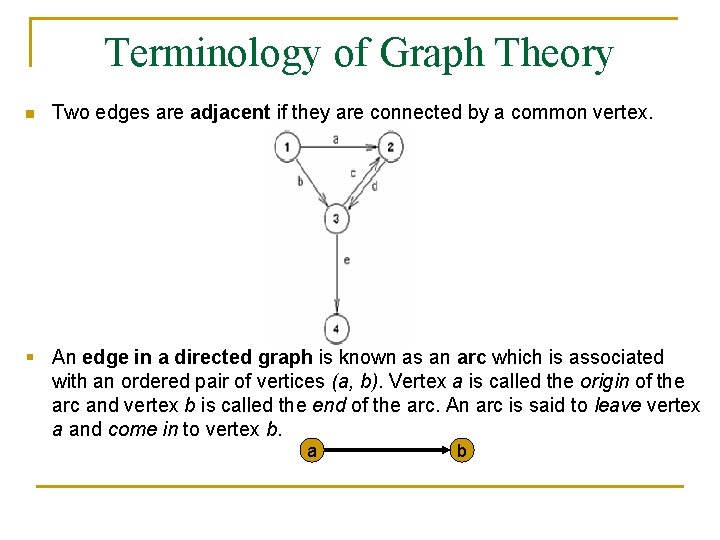
Terminology of Graph Theory n Two edges are adjacent if they are connected by a common vertex. § An edge in a directed graph is known as an arc which is associated with an ordered pair of vertices (a, b). Vertex a is called the origin of the arc and vertex b is called the end of the arc. An arc is said to leave vertex a and come in to vertex b. a b

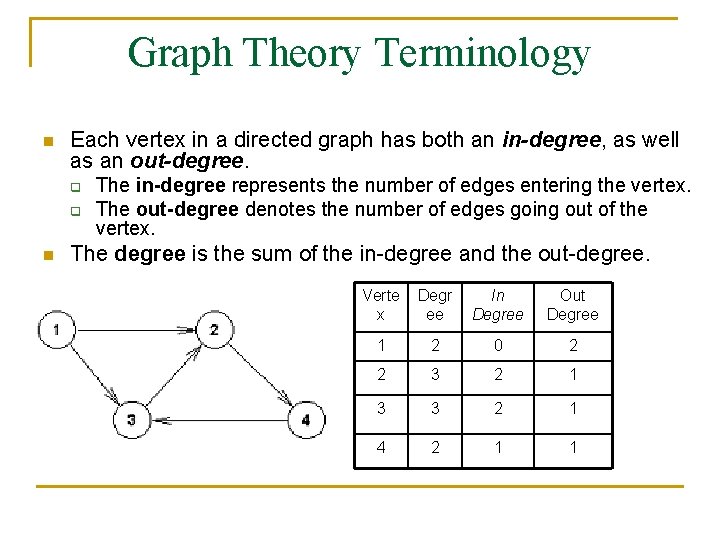
Graph Theory Terminology n Each vertex in a directed graph has both an in-degree, as well as an out-degree. q q n The in-degree represents the number of edges entering the vertex. The out-degree denotes the number of edges going out of the vertex. The degree is the sum of the in-degree and the out-degree. Verte x Degr ee In Degree Out Degree 1 2 0 2 2 3 2 1 3 3 2 1 4 2 1 1

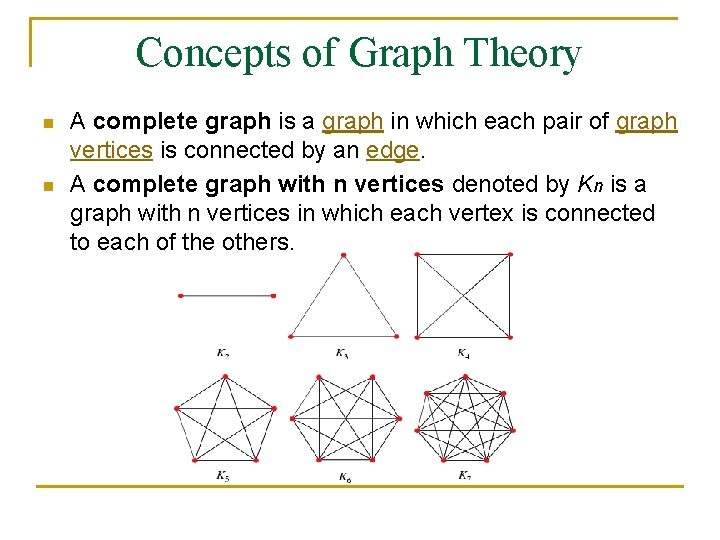
Concepts of Graph Theory n n A complete graph is a graph in which each pair of graph vertices is connected by an edge. A complete graph with n vertices denoted by Kn is a graph with n vertices in which each vertex is connected to each of the others.

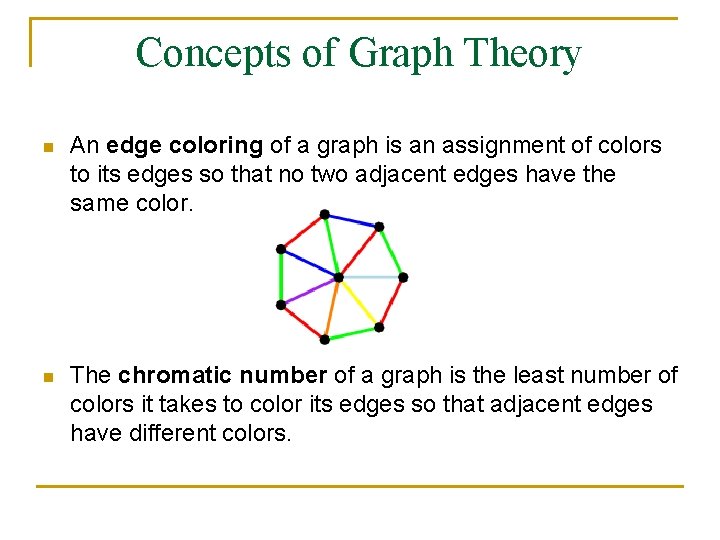
Concepts of Graph Theory n An edge coloring of a graph is an assignment of colors to its edges so that no two adjacent edges have the same color. n The chromatic number of a graph is the least number of colors it takes to color its edges so that adjacent edges have different colors.

Concepts of Graph Theory n A graph is bipartite if its vertices can be partitioned into two disjoint subsets U and V such that no two graph vertices within the same set are adjacent. U n V A Bipartite graph is a complete bipartite graph if every vertex in U is connected to every vertex in V. U V

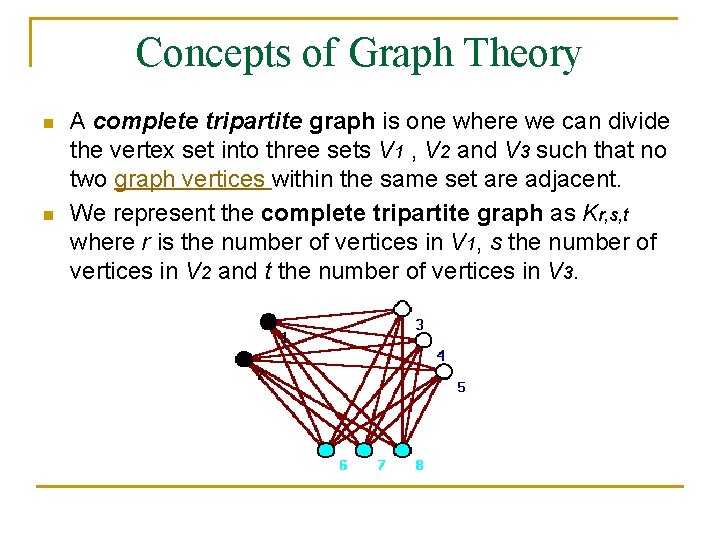
Concepts of Graph Theory n n A complete tripartite graph is one where we can divide the vertex set into three sets V 1 , V 2 and V 3 such that no two graph vertices within the same set are adjacent. We represent the complete tripartite graph as Kr, s, t where r is the number of vertices in V 1, s the number of vertices in V 2 and t the number of vertices in V 3.

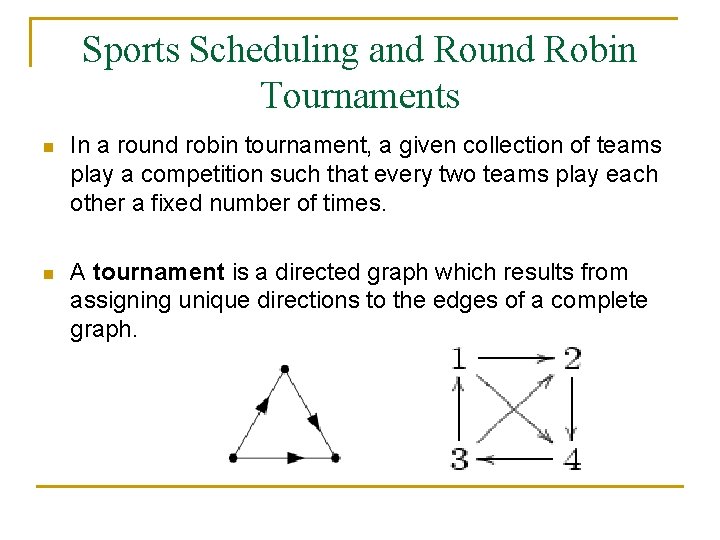
Sports Scheduling and Round Robin Tournaments n In a round robin tournament, a given collection of teams play a competition such that every two teams play each other a fixed number of times. n A tournament is a directed graph which results from assigning unique directions to the edges of a complete graph.

Representations of Graphs as they relate to Round Robin Tournaments n n We can represent every tournament by a tournament T where the vertices of T correspond to the individual teams. The teams are represented by points and for each pair of points an arc is drawn from the visiting team to the home team. 1 2 3 4

Representations of Graphs as they relate to Round Robin Tournaments n If a game i and j is played in the home-city of team i, it is a home game for i and an away game for j. Which can be represented by an arc (j, i). j i n Likewise, if the game is played in the home city of team j, the game can be represented by an arc (i, j). j i

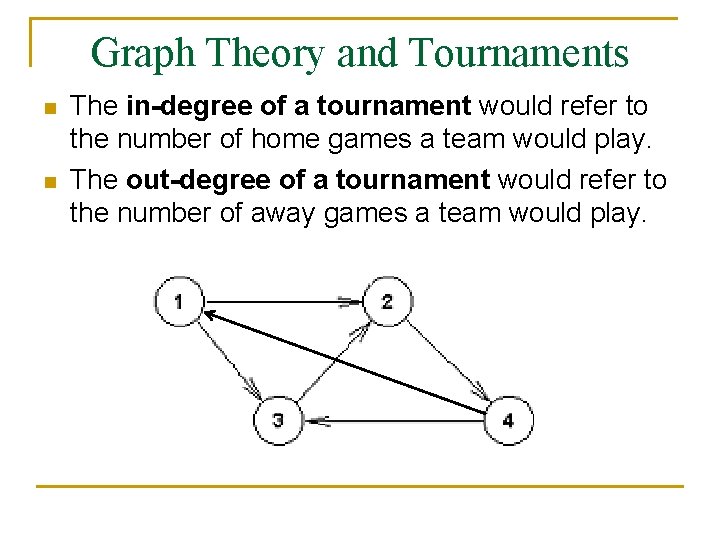
Graph Theory and Tournaments n n The in-degree of a tournament would refer to the number of home games a team would play. The out-degree of a tournament would refer to the number of away games a team would play.

Representations of Graphs as they relate to Round Robin Tournaments n An oriented coloring in tournaments is obtained by partitioning the edges into n color classes such that no two adjacent edges have the same color. T R B n F Such a coloring defines a schedule as the following: if arc (i, j) has color p, it means that team i and team j play against each other in the home city of team j on day p. i j Team i plays team j on the day assigned to the blue coloring.

Putting Everything Together: 1 3 n n n In this graph we have four teams: Team 1, Team 2, Team 3, and Team 4 Each edge represents a competition between each team that it connects q n 4 This graph represents a tournament T with four vertices. Each vertex of the graph represents an individual team, q n 2 In this graph their consists 6 edges and therefore there are 6 competitions in this tournament. For each pair of vertices an arc is drawn from the visiting team to the home team Each coloring corresponds to a specific day.

Scheduling for the NBA q q The National Basketball Association consists of thirty teams that play during a season running from the first week of November to the last week of April. The NBA is divided into two conferences which is even further divided into divisions such that each conference is divided into 3 divisions: q 1) The Eastern (15 Teams) q Atlantic Division (5 Teams) Central Division (5 Teams) q South East Division (5 Teams) q q 2) The Western (15 Teams) q q q North West Division (5 Teams) Pacific Division (5 Teams) South West Division (5 Teams)

Constraints for Scheduling the perfect NBA Season n Developing a schedule entails assigning a date for each of the 1, 140 games to be played, such that these certain requirements are met: q q Each team can only play one game on a given day. Twenty-four hour turn around period after each game. No team can play more than four home or away games in a row. Each team will play every team in their division four times: n q q Two of which must be away games and Two of which must be home games. Each team will play every team that is in their conference but not in their division three separate times. n Maximum of two home games for each team played. n Maximum of two away games for each team played. Each team will play every team that is not in their conference two times. n One of which must be an away game and One of which must be a home game.

Constraints for Scheduling the perfect NBA Season n Every Team will play 16 Division Games. q n Every Team Will Play 30 Conference Games. q n n Home and Away Games will vary. Every Team Will Play 30 Non-Conference Games. q n 8 Home Games and 8 Away Games 15 Home Games and 15 Away Games Therefore, each team will play a total of 76 games For a total of 1, 140 games to be scheduled. q q q 240 Division Games 450 Conference Games 450 Non-Conference Games

Scheduling for the NBA using Graph Theory Each NBA team will represent a vertex on the above map.

Scheduling for the NBA using Graph Theory n Divisions- Each Division is a Complete Graph with 5 vertices or T 5 1 2 4 3 5 n Conference- Each Conference is a Complete Tripartite Graph T 5, 5, 5 n Non-Conference (League)- A Complete Bipartite T 15, 15

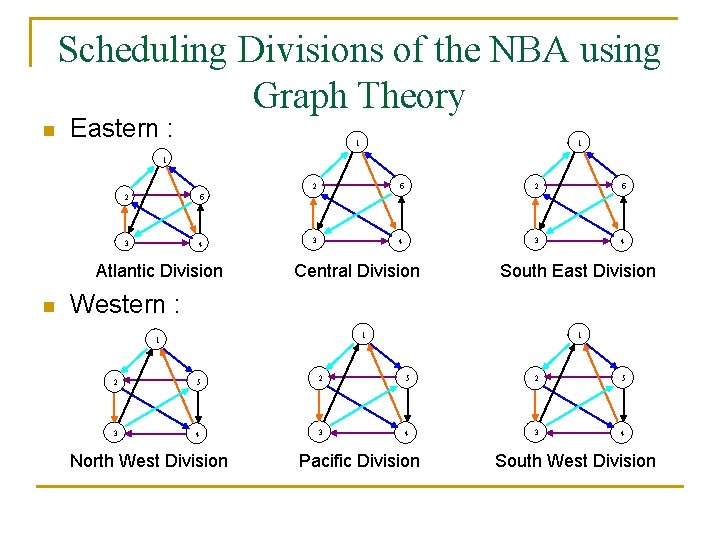
Scheduling Divisions of the NBA using Graph Theory n Eastern : 1 1 1 2 5 3 4 Atlantic Division n 2 5 3 4 Central Division South East Division Western : 1 1 1 2 5 2 5 3 4 3 4 North West Division Pacific Division South West Division

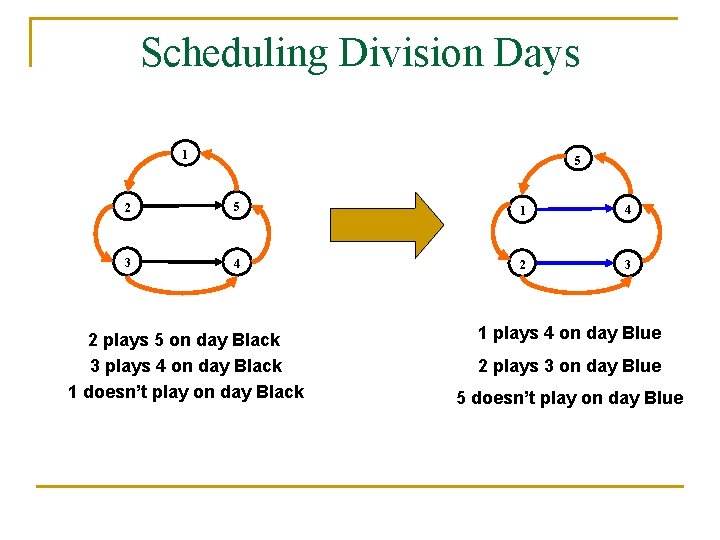
Scheduling Division Days 1 5 2 5 1 4 3 4 2 3 2 plays 5 on day Black 3 plays 4 on day Black 1 doesn’t play on day Black 1 plays 4 on day Blue 2 plays 3 on day Blue 5 doesn’t play on day Blue

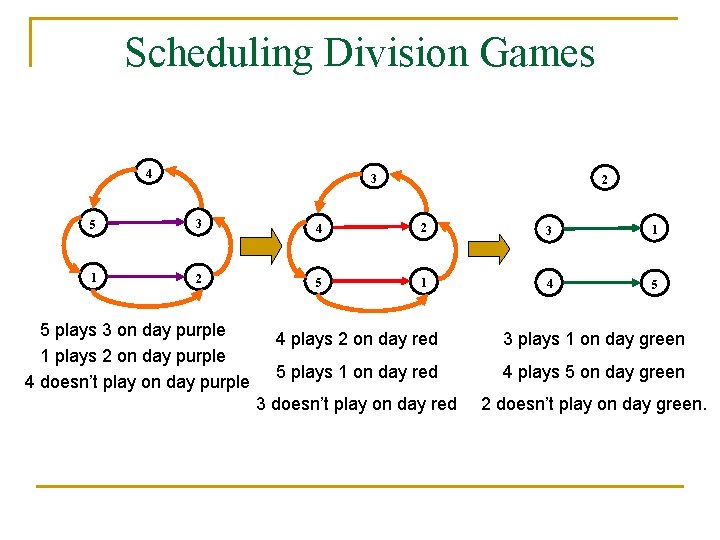
Scheduling Division Games 4 3 2 5 3 4 2 3 1 1 2 5 1 4 5 5 plays 3 on day purple 1 plays 2 on day purple 4 doesn’t play on day purple 4 plays 2 on day red 3 plays 1 on day green 5 plays 1 on day red 4 plays 5 on day green 3 doesn’t play on day red 2 doesn’t play on day green.

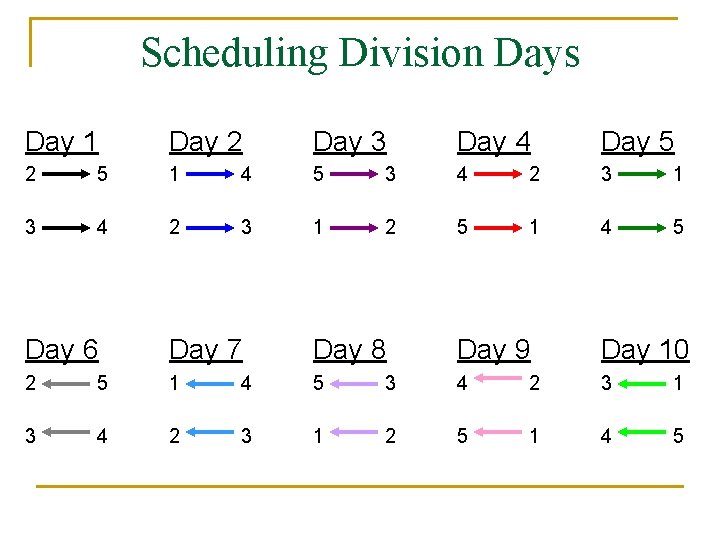
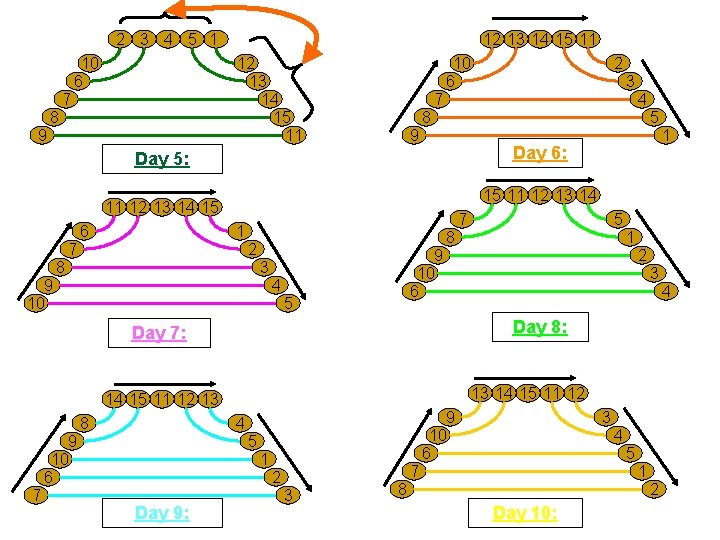
Scheduling Division Days Day 1 Day 2 Day 3 Day 4 Day 5 2 5 1 4 5 3 4 2 3 1 2 5 1 4 5 Day 6 Day 7 Day 8 Day 9 Day 10 2 5 1 4 5 3 4 2 3 1 2 5 1 4 5

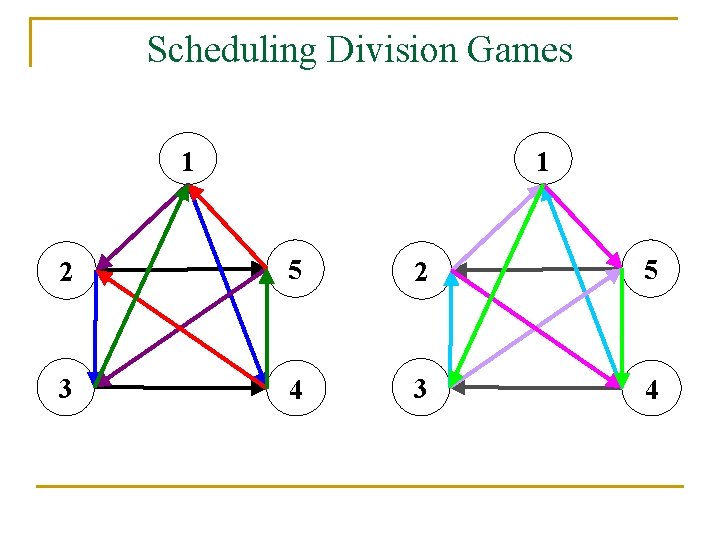
Scheduling Division Games 1 1 2 5 3 4

Scheduling Conference Games

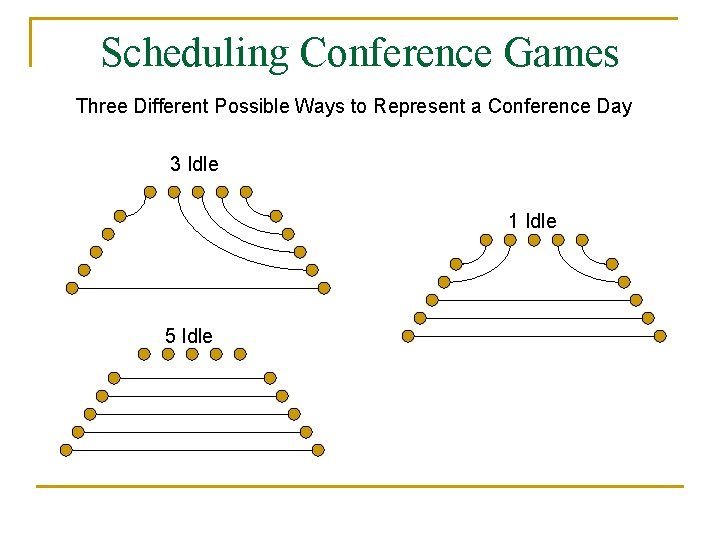
Scheduling Conference Games Three Different Possible Ways to Represent a Conference Day 3 Idle 1 Idle 5 Idle

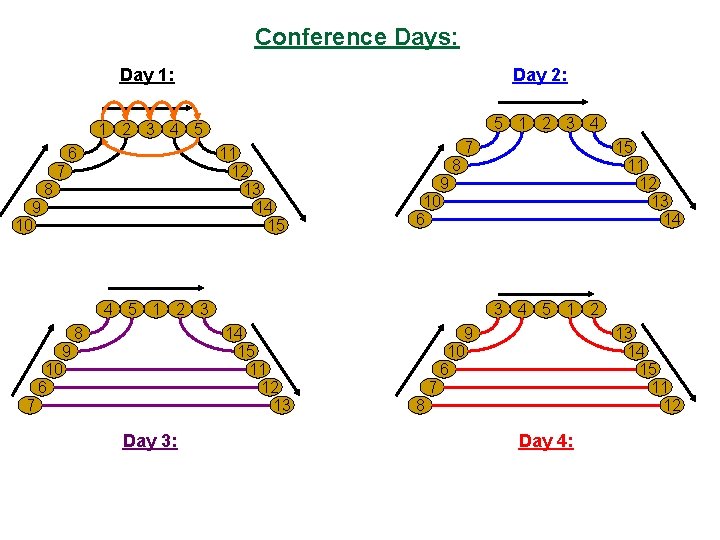
Conference Days: Day 1: Day 2: 5 1 2 3 4 5 6 11 12 13 14 15 7 8 9 10 6 4 5 1 2 3 8 3 4 5 1 2 14 15 11 12 13 9 10 6 7 Day 3: 15 11 12 13 14 9 10 6 13 14 15 11 12 7 8 Day 4:

2 3 4 5 1 10 6 12 13 14 15 11 7 8 9 10 6 4 8 5 9 15 11 12 13 14 7 1 7 8 4 5 2 3 4 Day 8: Day 7: 13 14 15 11 12 13 9 10 6 4 5 1 3 4 5 7 2 Day 9: 1 9 10 6 3 9 10 7 5 8 2 9 10 6 1 Day 6: 11 12 13 14 15 8 3 7 Day 5: 6 2 3 1 8 2 Day 10:

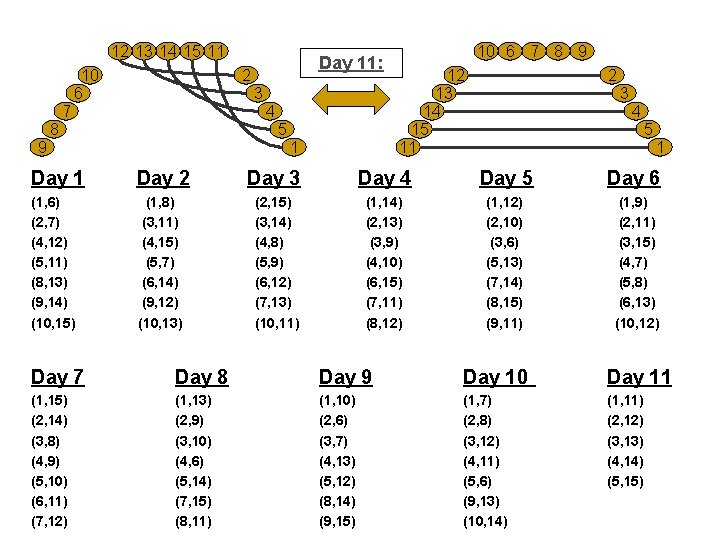
12 13 14 15 11 10 6 Day 11: 2 3 7 4 8 5 9 1 10 6 7 8 9 12 13 14 15 11 2 3 4 5 1 Day 2 Day 3 Day 4 Day 5 Day 6 (1, 6) (2, 7) (4, 12) (5, 11) (8, 13) (9, 14) (10, 15) (1, 8) (3, 11) (4, 15) (5, 7) (6, 14) (9, 12) (10, 13) (2, 15) (3, 14) (4, 8) (5, 9) (6, 12) (7, 13) (10, 11) (1, 14) (2, 13) (3, 9) (4, 10) (6, 15) (7, 11) (8, 12) (1, 12) (2, 10) (3, 6) (5, 13) (7, 14) (8, 15) (9, 11) (1, 9) (2, 11) (3, 15) (4, 7) (5, 8) (6, 13) (10, 12) Day 7 Day 8 Day 9 Day 10 Day 11 (1, 15) (2, 14) (3, 8) (4, 9) (5, 10) (6, 11) (7, 12) (1, 13) (2, 9) (3, 10) (4, 6) (5, 14) (7, 15) (8, 11) (1, 10) (2, 6) (3, 7) (4, 13) (5, 12) (8, 14) (9, 15) (1, 7) (2, 8) (3, 12) (4, 11) (5, 6) (9, 13) (10, 14) (1, 11) (2, 12) (3, 13) (4, 14) (5, 15)

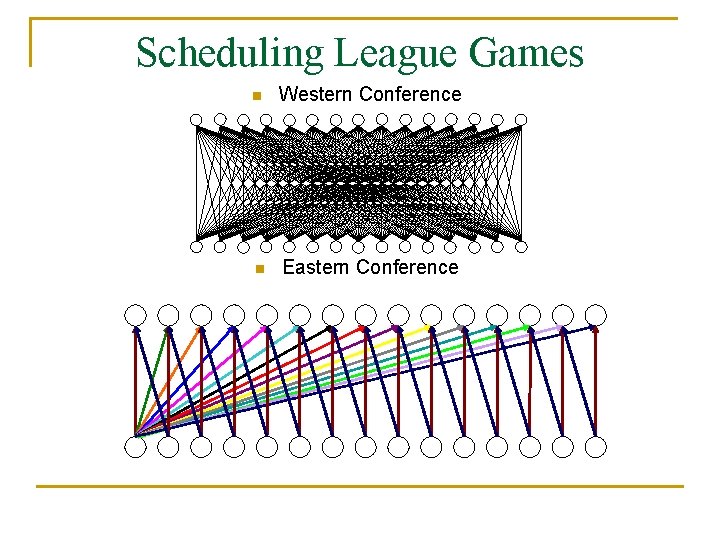
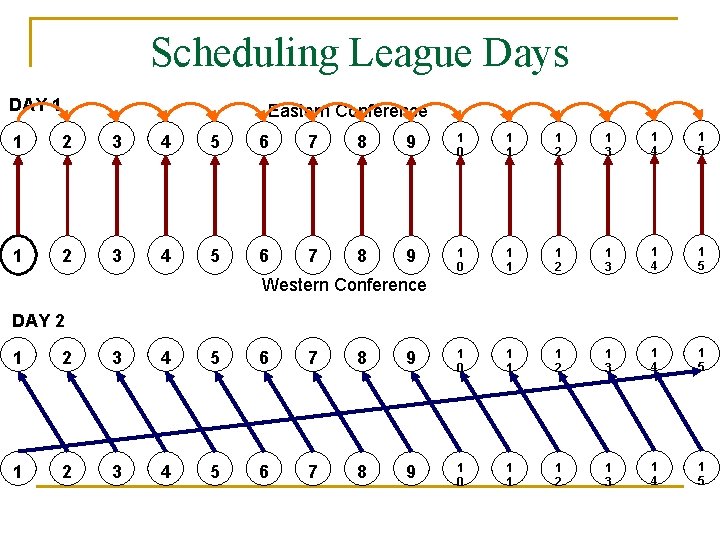
Scheduling League Games n Western Conference n Eastern Conference

Scheduling League Days DAY 1 Eastern Conference 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 Western Conference DAY 2 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5

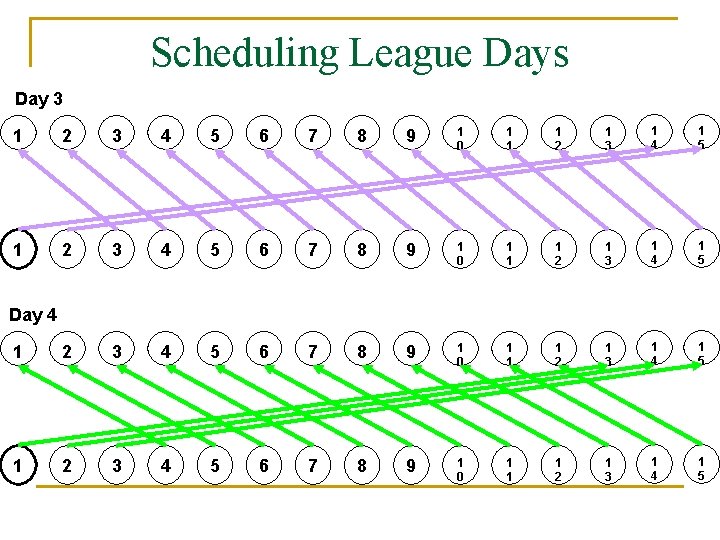
Scheduling League Days Day 3 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 Day 4

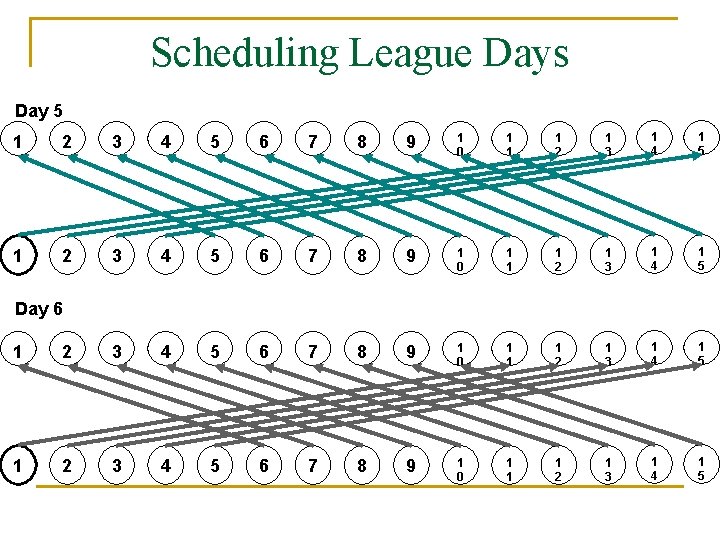
Scheduling League Days Day 5 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 Day 6 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5

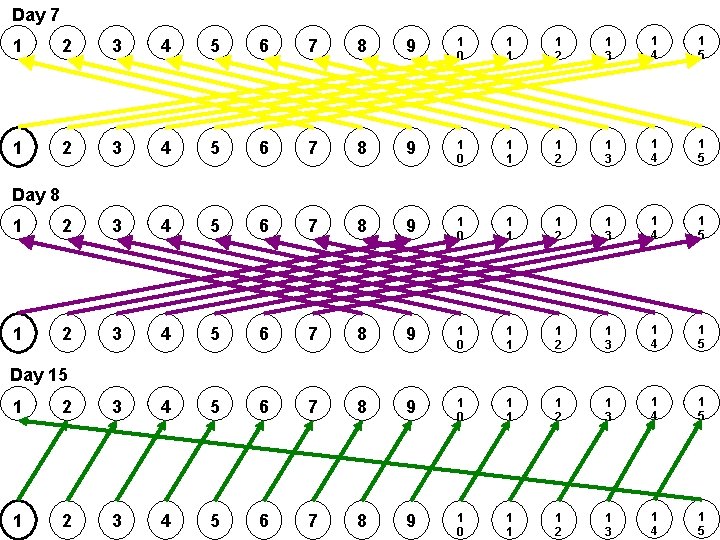
Day 7 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 Day 8 Day 15 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5

Day 1 (1, 1) (6, 6) (2, 2) (7, 7) (3, 3) (8, 8) (4, 4) (9, 9) (5, 5) (10, 10) (11, 11) (12, 12) (13, 13) (14, 14) (15, 15) Day 2 (1, 15) (6, 5) (2, 1) (7, 6) (3, 2) (8, 7) (4, 3) (9, 8) (5, 4) (10, 9) (11, 10) (12, 11) (13, 12) (14, 13) (15, 14) Day 3 (1, 14) (6, 4) (2, 15) (7, 5) (3, 1) (8, 6) (4, 2) (9, 7) (5, 3) (10, 8) (11, 9) (12, 10) (13, 11) (14, 12) (15, 13) Day 4 (1, 13) (6, 3) (11, 8) (2, 14) (7, 4) (12, 9) (3, 15) (8, 5) (13, 10) (4, 1) (9, 6) (14, 11) (5, 2) (10, 7) (15, 12) Day 5 (1, 12) (6, 2) (11, 7) (2, 13) (7, 3) (12, 8) (3, 14) (8, 4) (13, 9) (4, 15) (9, 5) (14, 10) (5, 1) (10, 6) (15, 11) Day 6 Day 7 Day 8 Day 9 Day 10 (1, 11) (6, 1) (11, 6) (2, 12) (7, 2) (12, 7) (3, 13) (8, 3) (13, 8) (4, 14) (9, 4) (14, 9) (5, 15) (10, 5) (15, 10) (1, 10) (6, 15) (11, 5) (2, 11) (7, 1) (12, 6) (3, 12) (8, 2) (13, 7) (4, 13) (9, 3) (14, 8) (5, 14) (10, 4) (15, 9) (1, 9) (6, 14) (11, 4) (2, 10) (7, 15) (12, 5) (3, 11) (8, 1) (13, 6) (4, 12) (9, 2) (14, 7) (5, 13) (10, 3) (15, 8) (1, 8) (6, 13) (11, 3) (2, 9) (7, 14) (12, 4) (3, 10) (8, 15) (13, 5) (4, 11) (9, 1) (14, 6) (5, 12) (10, 2) (15, 7) (1, 7) (6, 12) (11, 2) (2, 8) (7, 13) (12, 3) (3, 9) (8, 14) (13, 4) (4, 10) (9, 15) (14, 5) (5, 11) (10, 1) (15, 6) Day 11 Day 12 (1, 6) (6, 11) (11, 1) (2, 7) (7, 12) (12, 2) (3, 8) (8, 13) (13, 3) (4, 9) (9, 14) (14, 4) (5, 10) (10, 15) (15, 5) (1, 5) (6, 10) (11, 15) (2, 6) (7, 11) (12, 1) (3, 7) (8, 12) (13, 2) (4, 8) (9, 13) (14, 3) (5, 9) (10, 14) (15, 4) Day 13 (1, 4) (6, 9) (11, 14) (2, 5) (7, 10) (12, 15) (3, 6) (8, 11) (13, 1) (4, 7) (9, 12) (14, 2) (5, 8) (10, 13) (15, 3) Day 14 (1, 3) (6, 8) (11, 13) (2, 4) (7, 9) (12, 14) (3, 5) (8, 10) (13, 15) (4, 6) (9, 11) (14, 1) (5, 7) (10, 12) (15, 2) Day 15 (1, 2) (6, 7) (11, 12) (2, 3) (7, 8) (12, 13) (3, 4) (8, 9) (13, 14) (4, 5) (9, 10) (14, 15) (5, 6) (10, 11) (15, 1)

Conclusion n Scheduling the National Basketball Association is a large and difficult problem. The many complicated constraints involved make it nearly impossible to find a guaranteed optimal solution. We have found, however, the best possible schedule such that fatigue and stress for the NBA players is minimized.

Graph Theory Web Quest

THE END