Graph Theory 1 FUNDAMENTAL CONCEPTS Fundamental Concept Graph

Graph Theory 1 FUNDAMENTAL CONCEPTS Fundamental Concept Graph Theory

Agenda 2 1 WHAT IS A GRAPH? 2 PATHS, CYCLES, AND TRAILS 3 VERTEX DEGREE AND COUNTING 4 DIRECTED GRAPHS Fundamental Concept

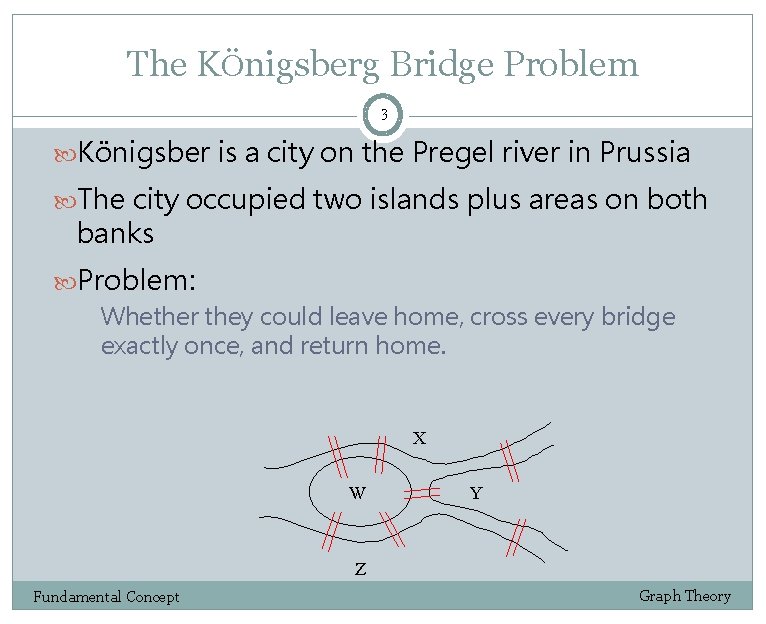
The KÖnigsberg Bridge Problem 3 Königsber is a city on the Pregel river in Prussia The city occupied two islands plus areas on both banks Problem: Whether they could leave home, cross every bridge exactly once, and return home. X W Y Z Fundamental Concept Graph Theory

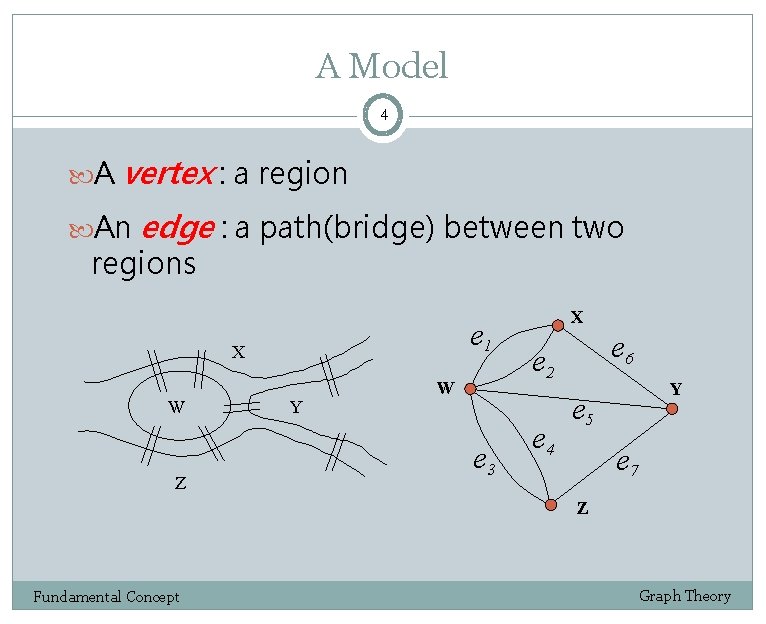
A Model 4 A vertex : a region An edge : a path(bridge) between two regions e 1 X W Z Y W e 3 X e 6 e 2 e 4 Y e 5 e 7 Z Fundamental Concept Graph Theory

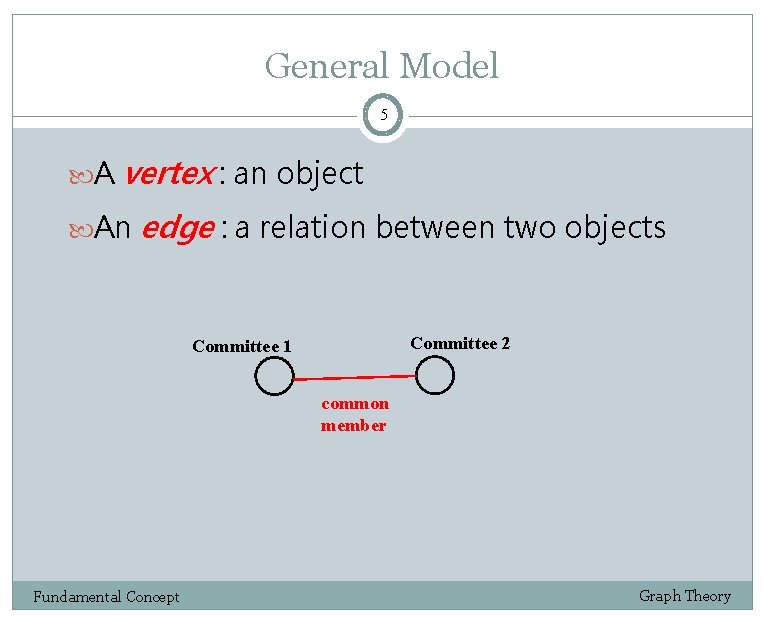
General Model 5 A vertex : an object An edge : a relation between two objects Committee 2 Committee 1 common member Fundamental Concept Graph Theory

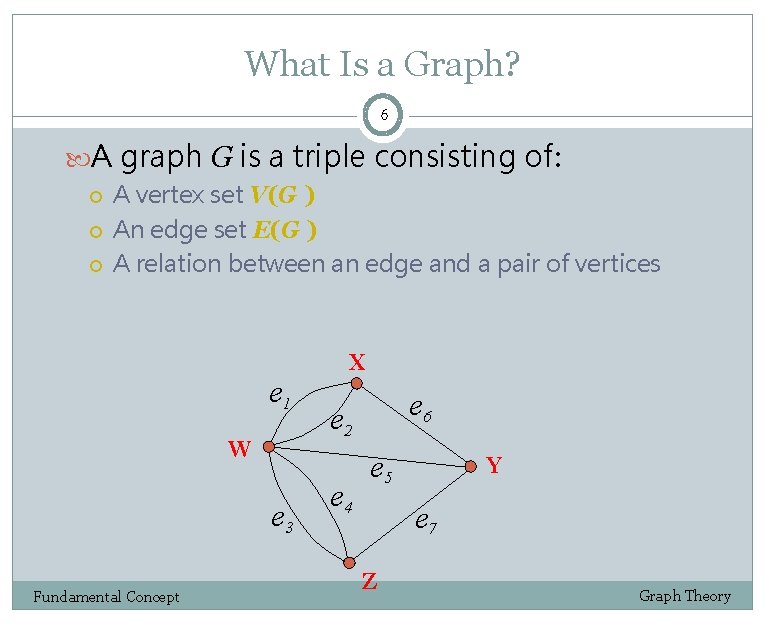
What Is a Graph? 6 A graph G is a triple consisting of: A vertex set V(G ) An edge set E(G ) A relation between an edge and a pair of vertices e 1 W e 3 Fundamental Concept X e 6 e 2 e 4 e 5 Y e 7 Z Graph Theory

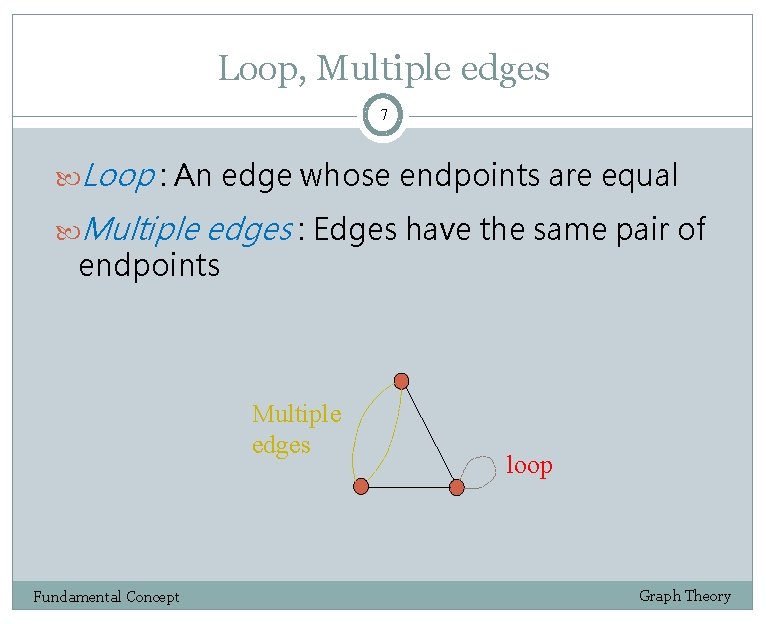
Loop, Multiple edges 7 Loop : An edge whose endpoints are equal Multiple edges : Edges have the same pair of endpoints Multiple edges Fundamental Concept loop Graph Theory

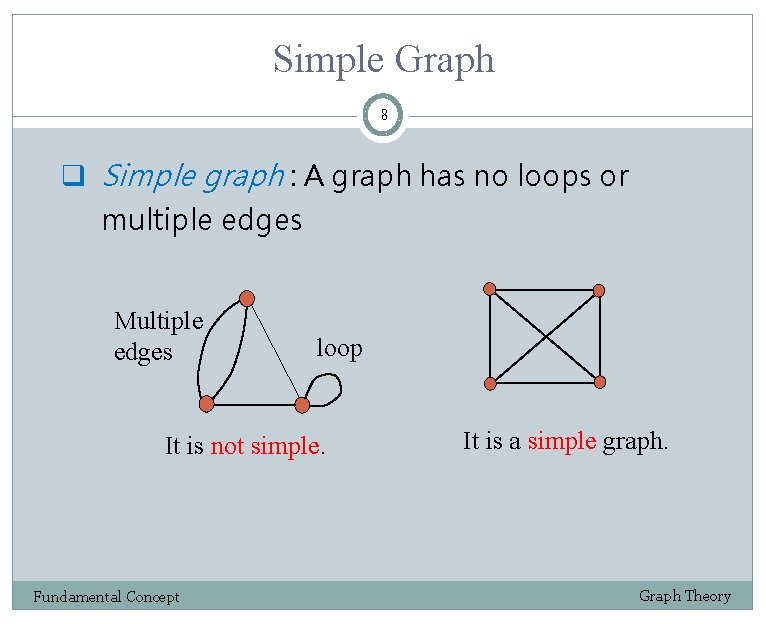
Simple Graph 8 q Simple graph : A graph has no loops or multiple edges Multiple edges loop It is not simple. Fundamental Concept It is a simple graph. Graph Theory

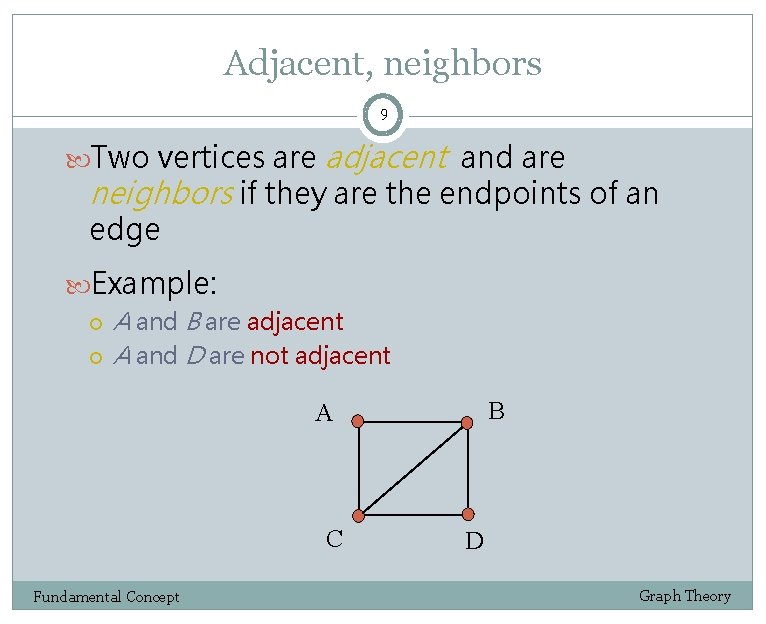
Adjacent, neighbors 9 Two vertices are adjacent and are neighbors if they are the endpoints of an edge Example: A and B are adjacent A and D are not adjacent B A C Fundamental Concept D Graph Theory

Finite Graph, Null Graph 10 Finite graph : an graph whose vertex set and edge set are finite Null graph : the graph whose vertex set and edges are empty Fundamental Concept Graph Theory

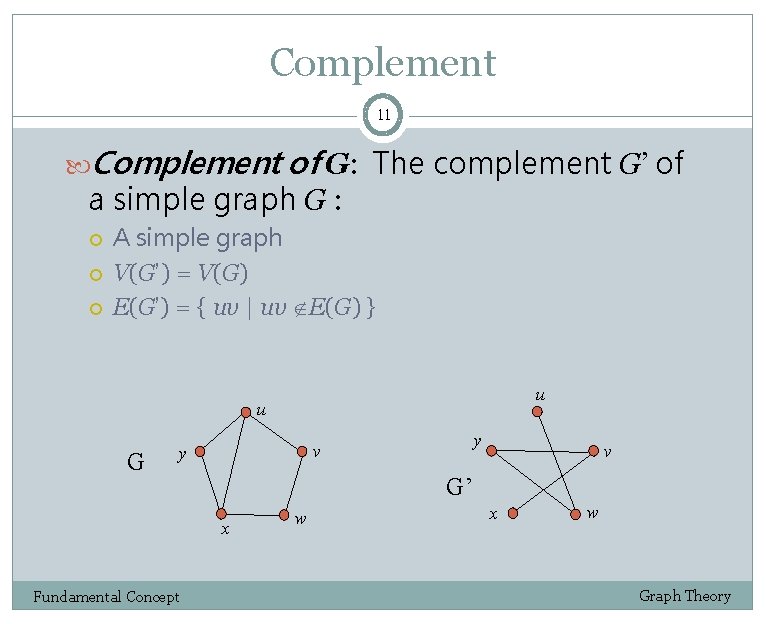
Complement 11 Complement of G: The complement G’ of a simple graph G : A simple graph V(G’) = V(G) E(G’) = { uv | uv E(G) } u u G v G’ x Fundamental Concept y v y w x w Graph Theory

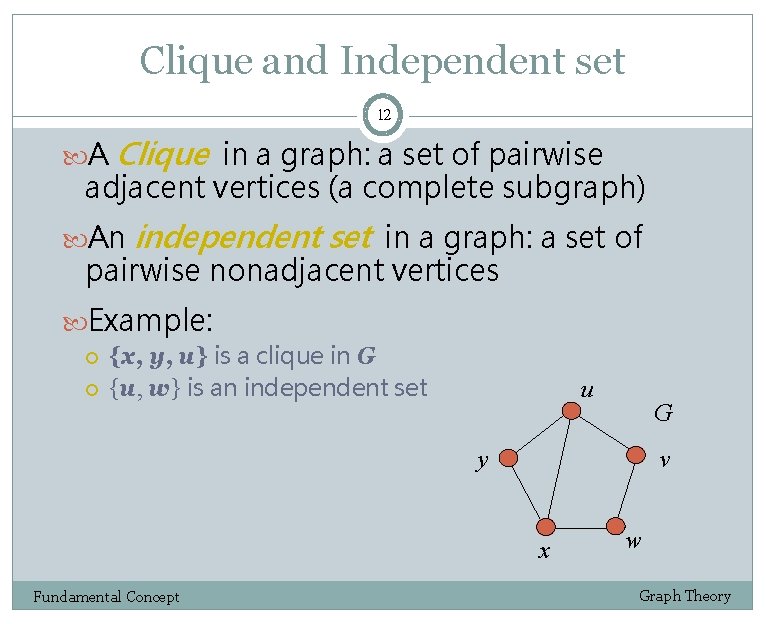
Clique and Independent set 12 A Clique in a graph: a set of pairwise adjacent vertices (a complete subgraph) An independent set in a graph: a set of pairwise nonadjacent vertices Example: {x, y, u} is a clique in G {u, w} is an independent set u G v y x Fundamental Concept w Graph Theory

Bipartite Graphs 13 A graph G is bipartite if V(G) is the union of two disjoint independent sets called partite sets of G Also: The vertices can be partitioned into two sets such that each set is independent Matching Problem Job Assignment Problem Boys Girls Fundamental Concept Workers Jobs Graph Theory

Chromatic Number 14 The chromatic number of a graph G, written x(G), is the minimum number of colors needed to label the vertices so that adjacent vertices receive different colors Blue Green x(G) = 3 Red Fundamental Concept Blue Graph Theory

Maps and coloring 15 A map is a partition of the plane into connected regions Can we color the regions of every map using at most four colors so that neighboring regions have different colors? Map Coloring graph coloring A region A vertex Adjacency An edge Fundamental Concept Graph Theory

Scheduling and graph Coloring 1 16 Two committees can not hold meetings at the same time if two committees have common member Committee 2 Committee 1 common member Fundamental Concept Graph Theory

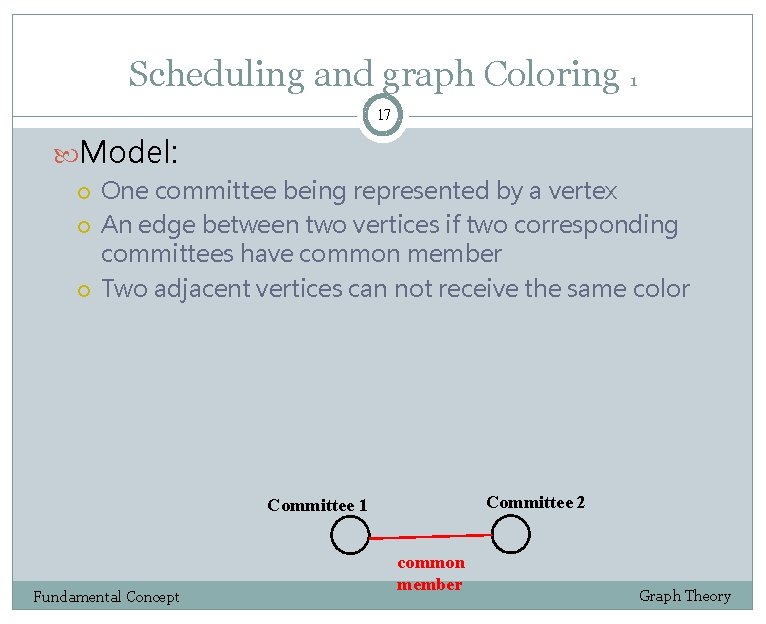
Scheduling and graph Coloring 1 17 Model: One committee being represented by a vertex An edge between two vertices if two corresponding committees have common member Two adjacent vertices can not receive the same color Committee 2 Committee 1 Fundamental Concept common member Graph Theory

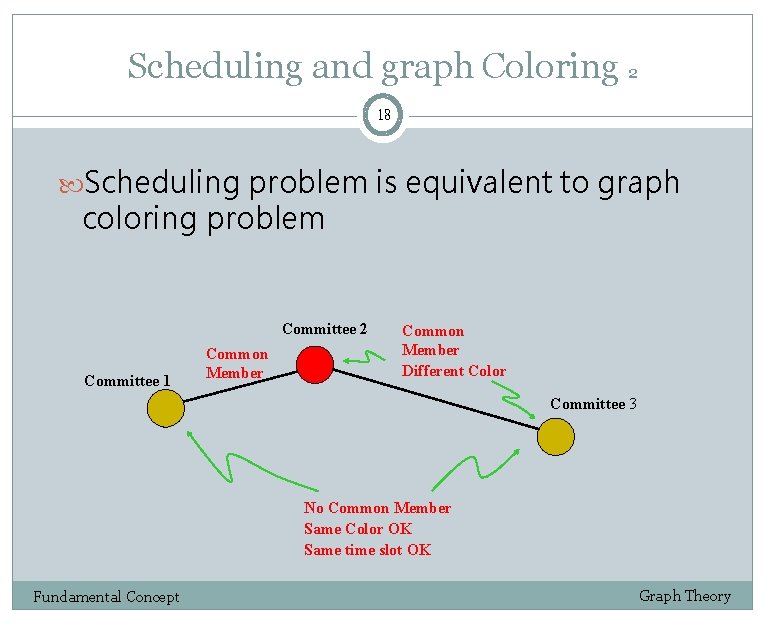
Scheduling and graph Coloring 2 18 Scheduling problem is equivalent to graph coloring problem Committee 2 Committee 1 Common Member Different Color Committee 3 No Common Member Same Color OK Same time slot OK Fundamental Concept Graph Theory

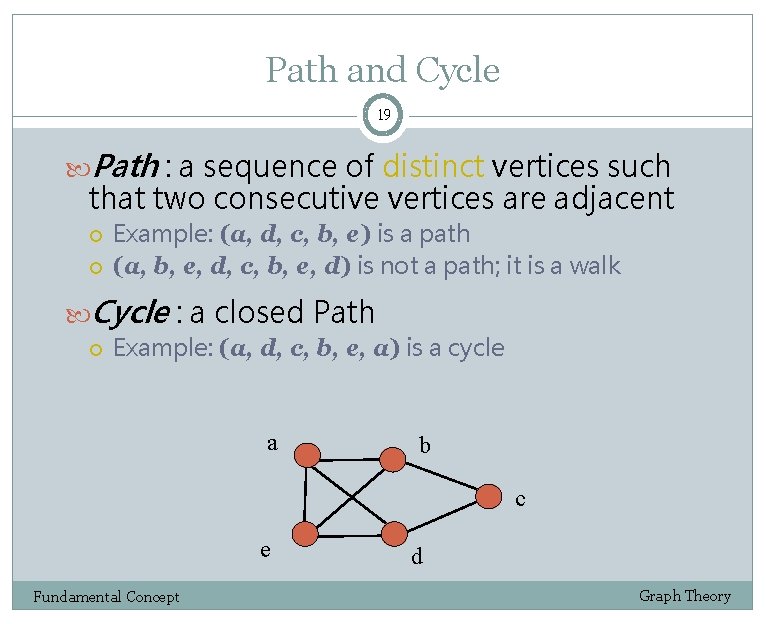
Path and Cycle 19 Path : a sequence of distinct vertices such that two consecutive vertices are adjacent Example: (a, d, c, b, e) is a path (a, b, e, d, c, b, e, d) is not a path; it is a walk Cycle : a closed Path Example: (a, d, c, b, e, a) is a cycle a b c e Fundamental Concept d Graph Theory

Subgraphs 20 A subgraph of a graph G is a graph H such that: V(H) V(G) and E(H) E(G) and The assignment of endpoints to edges in H is the same as in G. Fundamental Concept Graph Theory

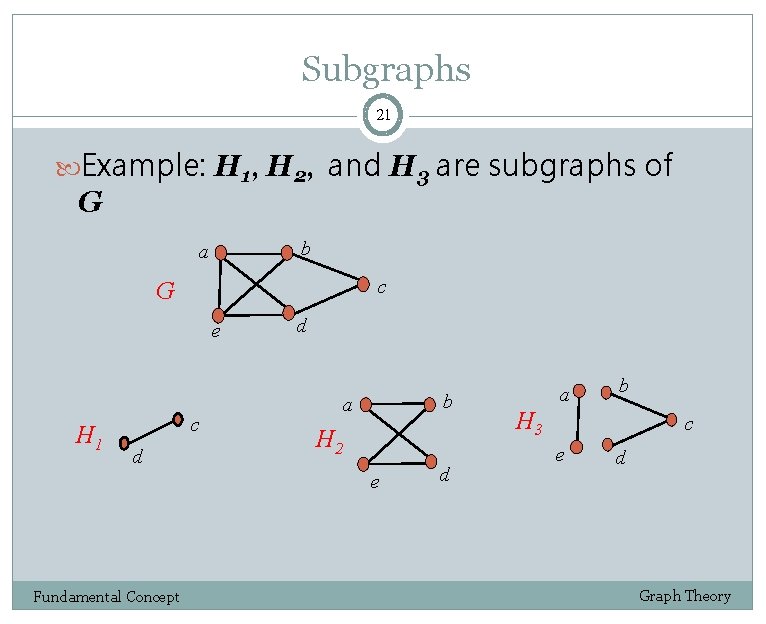
Subgraphs 21 Example: H 1, H 2, and H 3 are subgraphs of G b a c G e H 1 c d d b a H 2 e Fundamental Concept d a b H 3 c e d Graph Theory

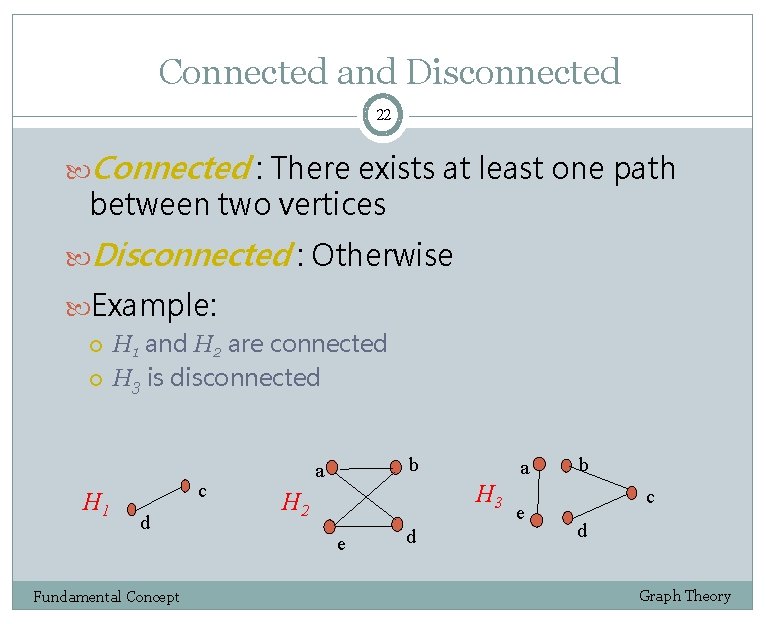
Connected and Disconnected 22 Connected : There exists at least one path between two vertices Disconnected : Otherwise Example: H 1 and H 2 are connected H 3 is disconnected c d Fundamental Concept b a a H 3 H 2 e d e b c d Graph Theory

Adjacency, Incidence, and Degree 23 Assume ei is an edge whose endpoints are (vj, vk) The vertices vj and vk are said to be adjacent The edge ei is said to be incident upon vj Degree of a vertex vk is the number of edges incident upon vk. It is denoted as d(vk) vj Fundamental Concept ei vk Graph Theory

Adjacency matrix 24 Let G = (V, E), |V| = n and |E|=m The adjacency matrix of G written A(G), is the n-by-n matrix in which entry ai, j is the number of edges in G with endpoints {vi, vj}. w b a x y c z e d Fundamental Concept w x y z w 0 1 1 0 x 1 0 2 0 y 1 2 0 1 z 0 0 1 0 Graph Theory

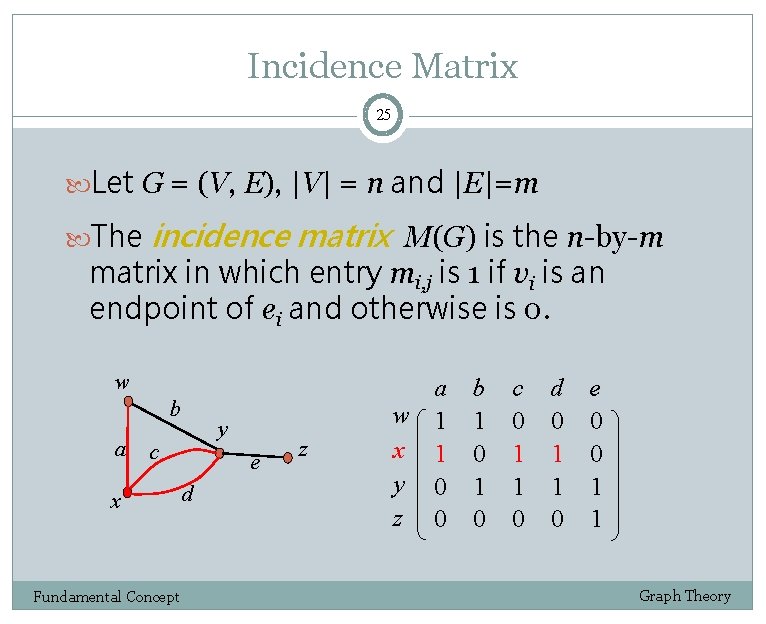
Incidence Matrix 25 Let G = (V, E), |V| = n and |E|=m The incidence matrix M(G) is the n-by-m matrix in which entry mi, j is 1 if vi is an endpoint of ei and otherwise is 0. w b a y c x Fundamental Concept e d z a b c d e w 1 1 0 0 0 x 1 0 1 1 0 y 0 1 1 z 0 0 1 Graph Theory

Isomorphism 26 An isomorphism from a simple graph G to a simple graph H is a bijection f: V(G) V(H) such that uv E(G) if and only if f(u)f(v) E(H) We say “G is isomorphic to H”, written G H w y c d H G x Fundamental Concept z a b f 1: w x y z c b d a f 2: w x y z a d b c Graph Theory

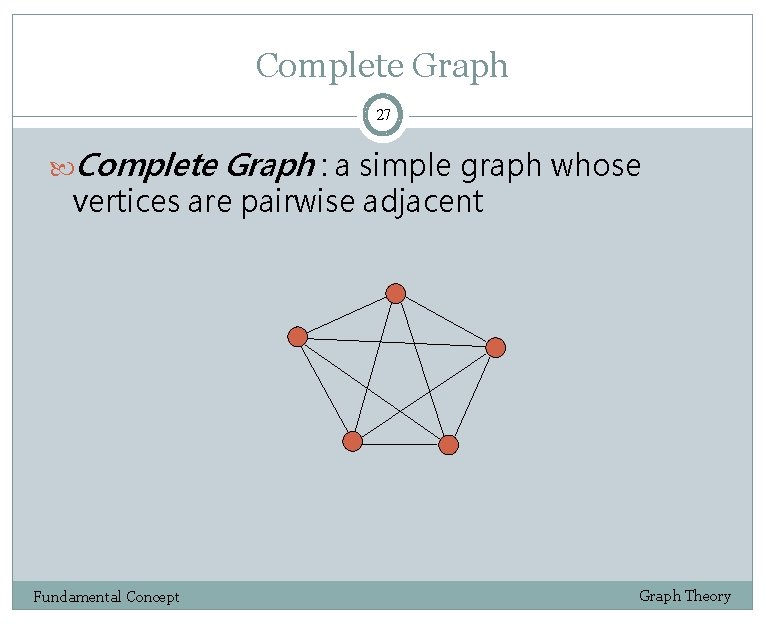
Complete Graph 27 Complete Graph : a simple graph whose vertices are pairwise adjacent Fundamental Concept Graph Theory

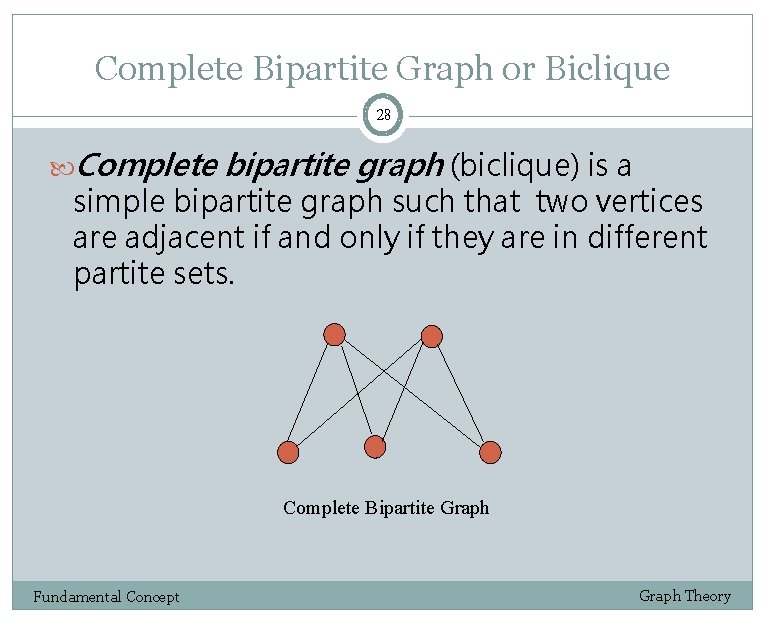
Complete Bipartite Graph or Biclique 28 Complete bipartite graph (biclique) is a simple bipartite graph such that two vertices are adjacent if and only if they are in different partite sets. Complete Bipartite Graph Fundamental Concept Graph Theory

Petersen Graph 1. 1. 36 29 The petersen graph is the simple graph whose vertices are the 2 -element subsets of a 5 -element set and whose edges are pairs of disjoint 2 -element subsets Fundamental Concept Graph Theory

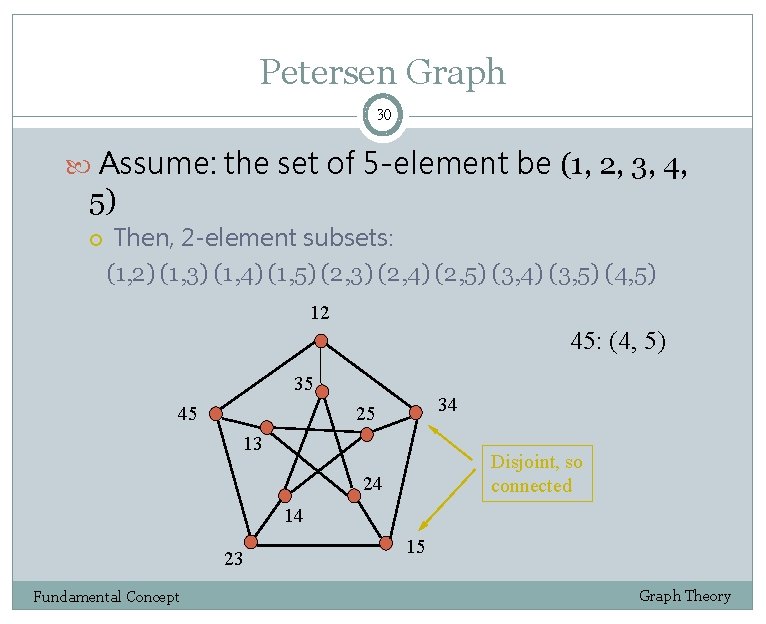
Petersen Graph 30 Assume: the set of 5 -element be (1, 2, 3, 4, 5) Then, 2 -element subsets: (1, 2) (1, 3) (1, 4) (1, 5) (2, 3) (2, 4) (2, 5) (3, 4) (3, 5) (4, 5) 12 45: (4, 5) 35 45 34 25 13 Disjoint, so connected 24 14 23 Fundamental Concept 15 Graph Theory

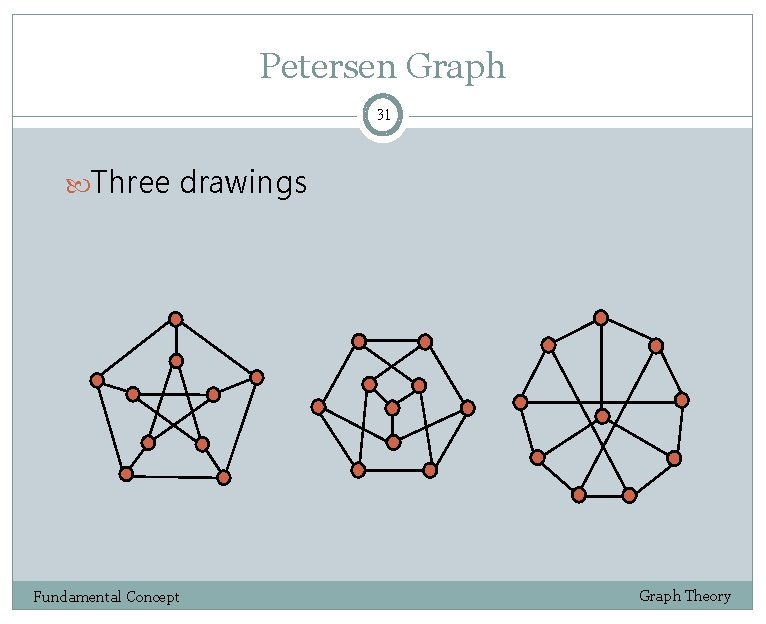
Petersen Graph 31 Three drawings Fundamental Concept Graph Theory

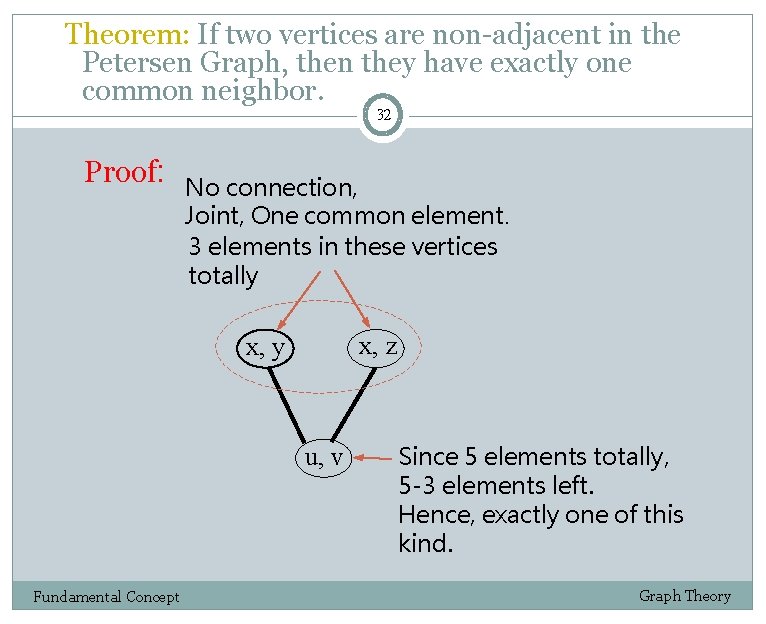
Theorem: If two vertices are non-adjacent in the Petersen Graph, then they have exactly one common neighbor. 32 Proof: No connection, Joint, One common element. 3 elements in these vertices totally x, z x, y u, v Fundamental Concept Since 5 elements totally, 5 -3 elements left. Hence, exactly one of this kind. Graph Theory

Girth 33 Girth : the length of its shortest cycle. If no cycles, girth is infinite Fundamental Concept Graph Theory

Girth and Petersen graph 34 Theorem: The Petersen Graph has girth 5. Proof: Simple no loop no 1 -cycle (cycle of length 1) Simple no multiple no 2 -cycle 5 elements no three pair-disjoint 2 -sets no 3 -cycle By previous theorem, two nonadjacent vertices has exactly one common neighbor no 4 -cycle 12 -34 -51 -23 -45 -12 is a 5 -cycle. Fundamental Concept Graph Theory

Walks, Trails 35 A walk : a list of vertices and edges v 0, e 1, v 1, …. , ek, vk such that, for 1 i k, the edge ei has endpoints vi-1 and vi. A trail : a walk with no repeated edge. Fundamental Concept Graph Theory

Paths 36 A u, v-walk or u, v-trail has first vertex u and last vertex v; these are its endpoints. A u, v-path: a u, v-trail with no repeated vertex. The length of a walk, trail, path, or cycle is its number of edges. A walk or trail is closed if its endpoints are the same. Fundamental Concept Graph Theory

Lemma: Every u, v-walk contains a u, v-path 37 Proof: Use induction on the length of a u, v-walk W. Basis step: l = 0. Having no edge, W consists of a single vertex (u=v). This vertex is a u, v-path of length 0. Induction step : l 1. Suppose that the claim holds for walks of length less than l. If W has no repeated vertex, then its vertices and edges form a u, v-path. Fundamental Concept Graph Theory

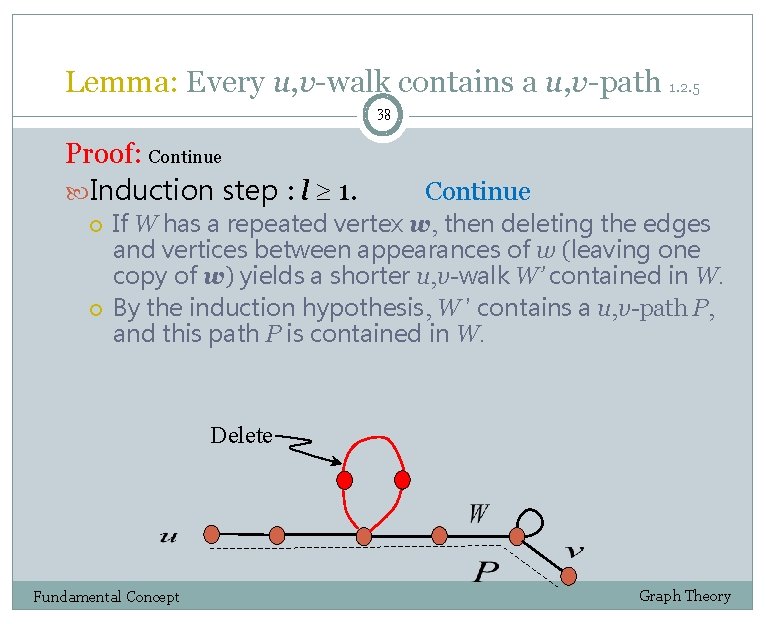
Lemma: Every u, v-walk contains a u, v-path 1. 2. 5 38 Proof: Continue Induction step : l 1. Continue If W has a repeated vertex w, then deleting the edges and vertices between appearances of w (leaving one copy of w) yields a shorter u, v-walk W’ contained in W. By the induction hypothesis, W ’ contains a u, v-path P, and this path P is contained in W. Delete Fundamental Concept Graph Theory

Components 39 The components of a graph G are its maximal connected subgraphs A component (or graph) is trivial if it has no edges; otherwise it is nontrivial An isolated vertex is a vertex of degree 0 Fundamental Concept Graph Theory

Theorem: Every graph with n vertices and k edges has at least n-k components 40 Proof: An n-vertex graph with no edges has n components Each edge added reduces this by at most 1 If k edges are added, then the number of components is at least n - k Fundamental Concept Graph Theory

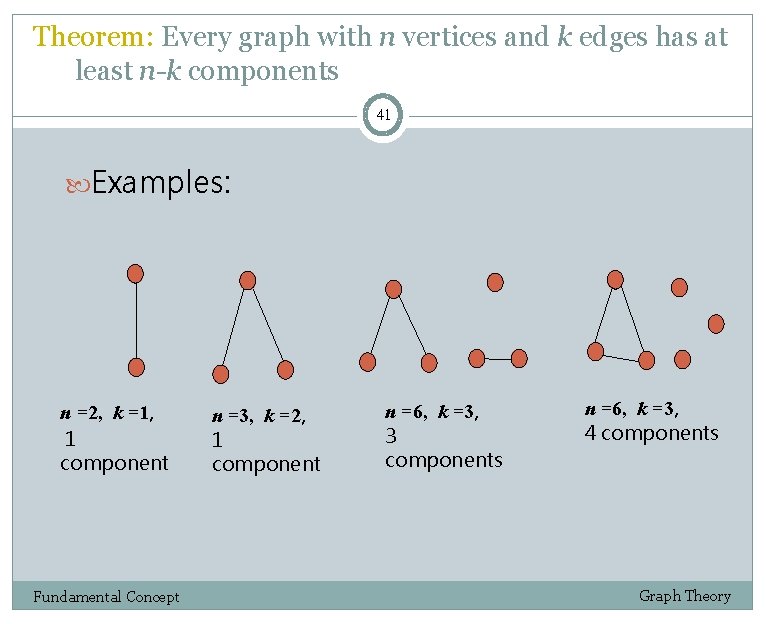
Theorem: Every graph with n vertices and k edges has at least n-k components 41 Examples: n =2, k =1, 1 component Fundamental Concept n =3, k =2, 1 component n =6, k =3, 3 components n =6, k =3, 4 components Graph Theory

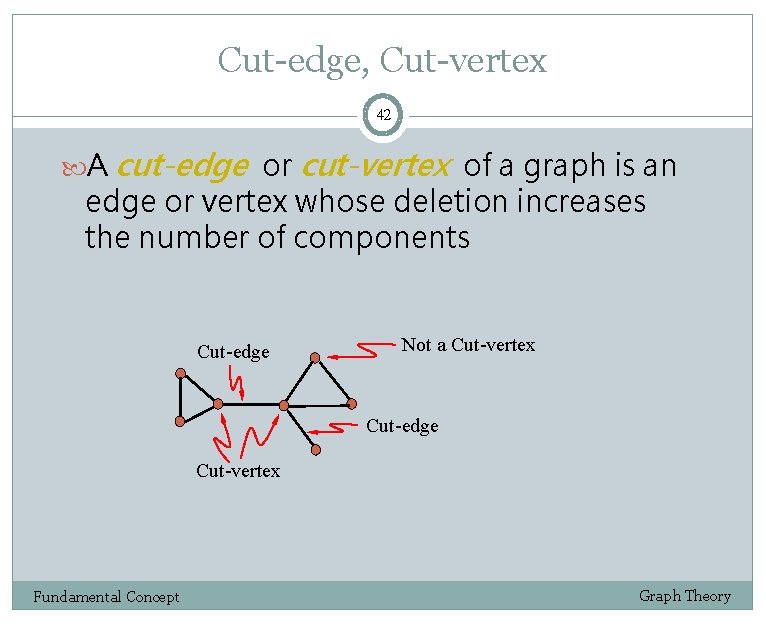
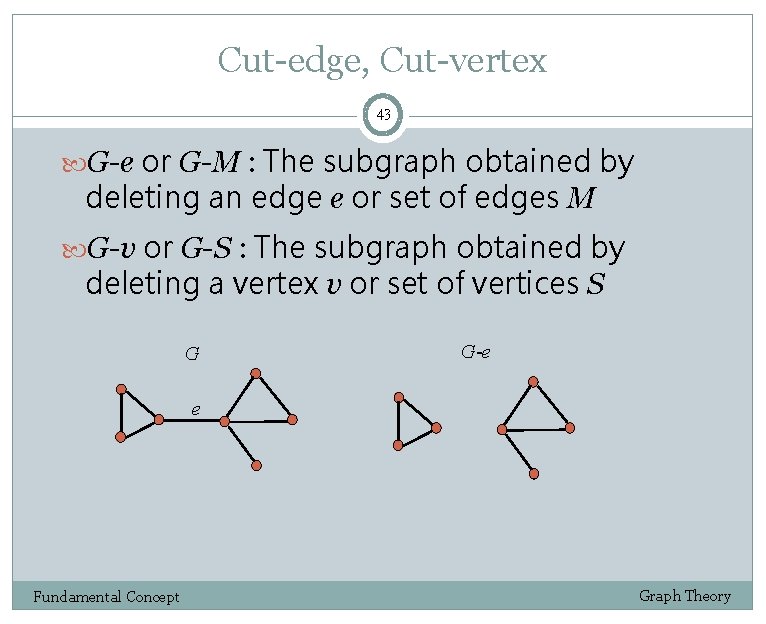
Cut-edge, Cut-vertex 42 A cut-edge or cut-vertex of a graph is an edge or vertex whose deletion increases the number of components Cut-edge Not a Cut-vertex Cut-edge Cut-vertex Fundamental Concept Graph Theory

Cut-edge, Cut-vertex 43 G-e or G-M : The subgraph obtained by deleting an edge e or set of edges M G-v or G-S : The subgraph obtained by deleting a vertex v or set of vertices S G G-e e Fundamental Concept Graph Theory

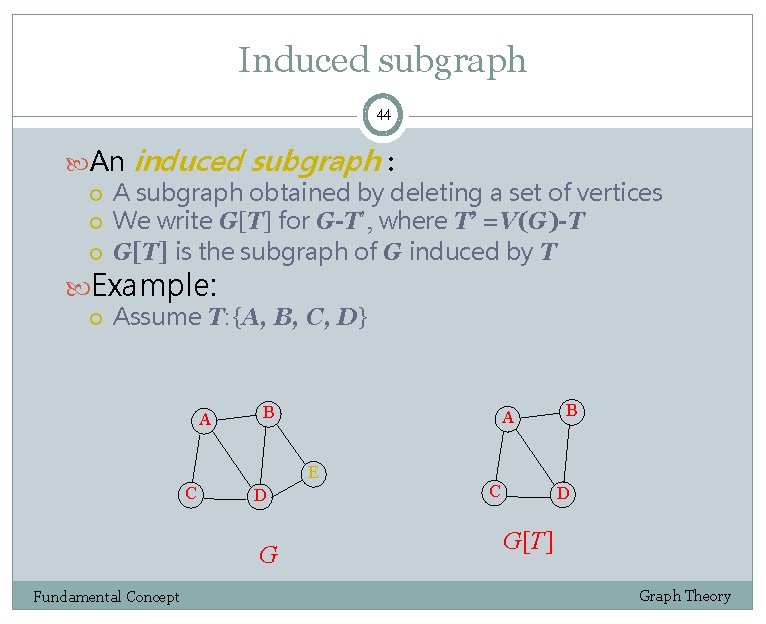
Induced subgraph 44 An induced subgraph : A subgraph obtained by deleting a set of vertices We write G[T] for G-T’, where T’ =V(G)-T G[T] is the subgraph of G induced by T Example: Assume T: {A, B, C, D} A B A E C D G Fundamental Concept C B D G[T] Graph Theory

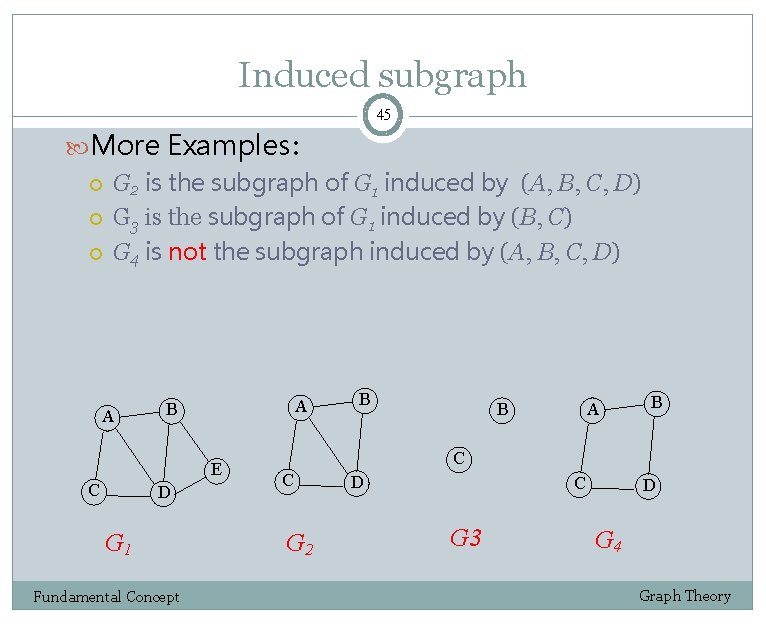
Induced subgraph 45 More Examples: G 2 is the subgraph of G 1 induced by (A, B, C, D) G 3 is the subgraph of G 1 induced by (B, C) G 4 is not the subgraph induced by (A, B, C, D) A A B E C D G 1 Fundamental Concept B B A B C C G 2 D C G 3 D G 4 Graph Theory

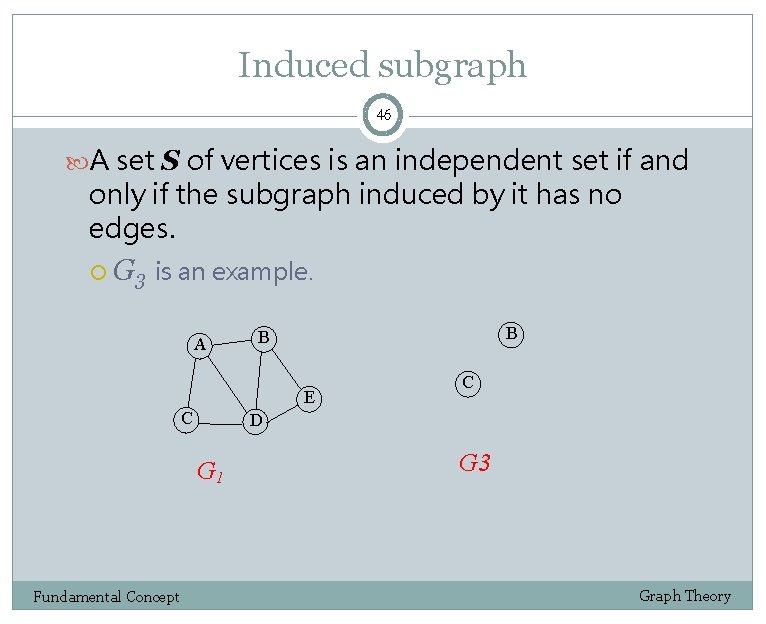
Induced subgraph 46 A set S of vertices is an independent set if and only if the subgraph induced by it has no edges. G 3 is an example. A B B E C D G 1 Fundamental Concept C G 3 Graph Theory

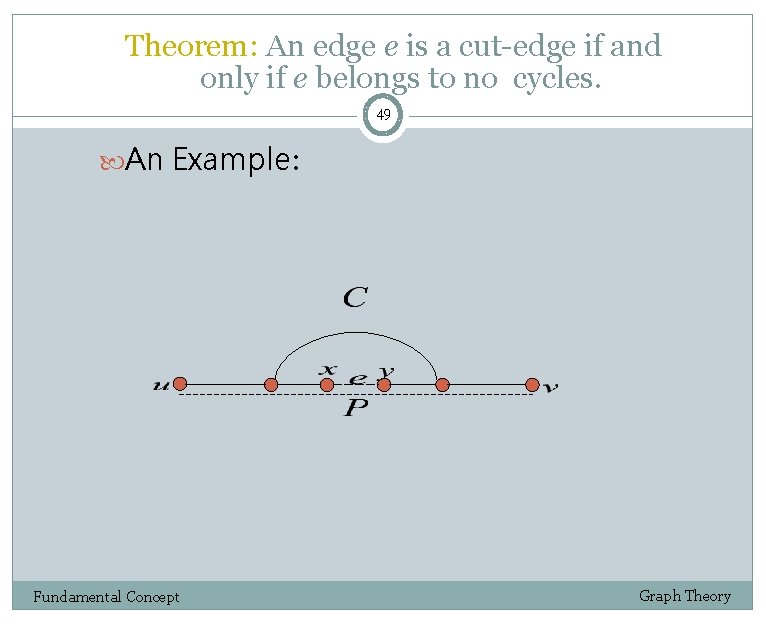
Theorem: An edge e is a cut-edge if and only if e belongs to no cycles. 47 Proof : 1/2 Let e= (x, y) be an edge in a graph G and H be the component containing e. Since deletion of e effects no other component, it suffices to prove that H-e is connected if and only if e belongs to a cycle. First suppose that H-e is connected. This implies that H-e contains an x, y-path, This path completes a cycle with e. Fundamental Concept Graph Theory

Theorem: An edge e is a cut-edge if and only if e belongs to no cycles. 48 Proof : 2/2 Now suppose that e lies in a cycle C. Choose u, v V(H) Since H is connected, H has a u, v-path P If P does not contain e Then P exists in H-e Otherwise (P contains e) Suppose by symmetry that x is between u and y on P Since H-e contains a u, x-path along P, the transitivity of the connection relation implies that H-e has a u, v-path We did this for all u, v V(H), so H-e is connected. Fundamental Concept Graph Theory

Theorem: An edge e is a cut-edge if and only if e belongs to no cycles. 49 An Example: Fundamental Concept Graph Theory

Lemma: Every closed odd walk contains an odd cycle 50 Proof: 1/3 Use induction on the length l of a closed odd walk W. l=1. A closed walk of length 1 traverses a cycle of length 1. We need to prove the claim holds if it holds for closed odd walks shorter than W. Fundamental Concept Graph Theory

Lemma: Every closed odd walk contains an odd cycle 51 Proof: 2/3 Suppose that the claim holds for closed odd walks shorter than W. If W has no repeated vertex (other than first = last), then W itself forms a cycle of odd length. Otherwise, (W has repeated vertex ) Need to prove: If repeated, W includes a shorter closed odd walk. By induction, theorem hold Fundamental Concept Graph Theory

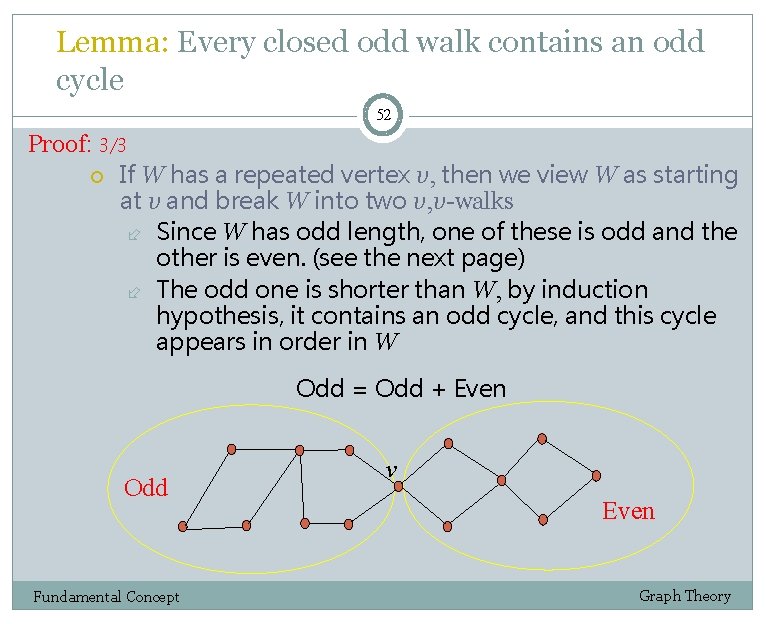
Lemma: Every closed odd walk contains an odd cycle 52 Proof: 3/3 If W has a repeated vertex v, then we view W as starting at v and break W into two v, v-walks Since W has odd length, one of these is odd and the other is even. (see the next page) The odd one is shorter than W, by induction hypothesis, it contains an odd cycle, and this cycle appears in order in W Odd = Odd + Even Odd Fundamental Concept v Even Graph Theory

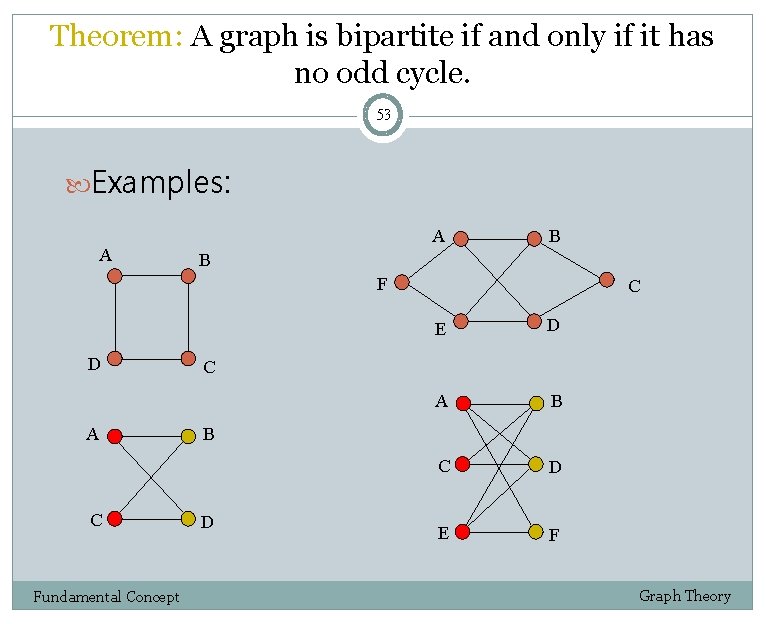
Theorem: A graph is bipartite if and only if it has no odd cycle. 53 Examples: A A B B F D A C Fundamental Concept C E D A B C D E F C B D Graph Theory

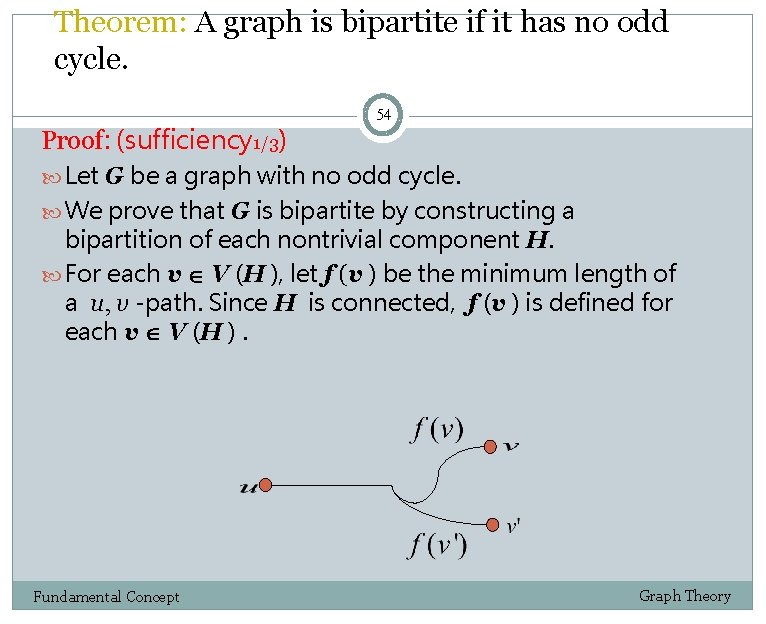
Theorem: A graph is bipartite if it has no odd cycle. Proof: (sufficiency 1/3) 54 Let G be a graph with no odd cycle. We prove that G is bipartite by constructing a bipartition of each nontrivial component H. For each v V (H ), let f (v ) be the minimum length of a u, v -path. Since H is connected, f (v ) is defined for each v V (H ). Fundamental Concept Graph Theory

Theorem: A graph is bipartite if it has no odd cycle. 55 Proof: (sufficiency 2/3) Let X={v V (H ): f (v ) is even} and Y={v V(H ): f (v ) is odd} An edge v, v’ within X (or Y ) would create a closed odd walk using a shortest u, v-path, the edge v, v’ within X (or Y ) and the reverse of a shortest u, v’-path. A closed odd walk using 1) a shortest u, v-path, 2) the edge v, v’ within X (or Y) , and 3) the reverse of a shortest u, v’-path. Fundamental Concept Graph Theory

Theorem: A graph is bipartite if it has no odd cycle. 56 Proof: (sufficiency 3/3) By Lemma 1. 2. 15, such a walk must contain an odd cycle, which contradicts our hypothesis Hence X and Y are independent sets. Also X Y = V(H), so H is an X, Y-bipartite graph Even (or Odd) Odd Cycle Even (or Odd) Fundamental Concept Because: even (or odd) + even (or odd) = even + 1 = odd Since no odd cycles, vv’ doesn’t exist. We have: X and Y are independent sets Graph Theory

Theorem: A graph is bipartite only if it has no odd cycle. 57 Proof: (necessity) Let G be a bipartite graph. Every walk alternates between the two sets of a bipartition So every return to the original partite set happens after an even number of steps Hence G has no odd cycle Fundamental Concept Graph Theory

Eulerian Circuits 58 A graph is Eulerian if it has a closed trail containing all edges. We call a closed trail a circuit when we do not specify the first vertex but keep the list in cyclic order. An Eulerian circuit or Eulerian trail in a graph is a circuit or trail containing all the edges. Fundamental Concept Graph Theory

Even Graph, Even Vertex 59 An even graph is a graph with vertex degrees all even. A vertex is odd [even] when its degree is odd [even]. Fundamental Concept Graph Theory

Maximal Path 60 A maximal path in a graph G is a path P in G that is not contained in a longer path. When a graph is finite, no path can extend forever , so maximal (non-extendible) paths exist. Fundamental Concept Graph Theory

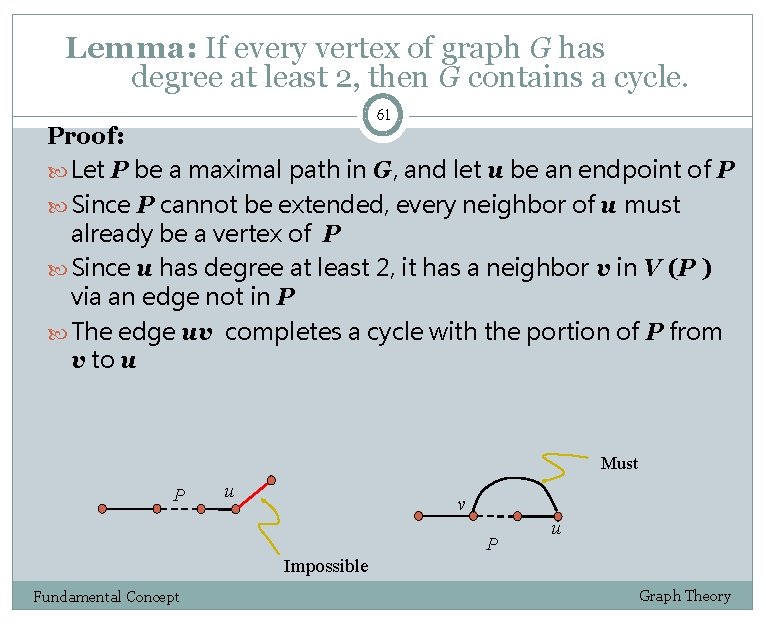
Lemma: If every vertex of graph G has degree at least 2, then G contains a cycle. 61 Proof: Let P be a maximal path in G, and let u be an endpoint of P Since P cannot be extended, every neighbor of u must already be a vertex of P Since u has degree at least 2, it has a neighbor v in V (P ) via an edge not in P The edge uv completes a cycle with the portion of P from v to u Must P u v P u Impossible Fundamental Concept Graph Theory

Theorem: A graph G is Eulerian if and only if it has at most one nontrivial component and its vertices all have even degree. 62 Proof: (Necessity) Suppose that G has an Eulerian circuit C Each passage of C through a vertex uses two incident edges And the first edge is paired with the last at the first vertex Hence every vertex has even degree In End (The last) Fundamental Concept Start (The 1 st) Out Graph Theory

Theorem: A graph G is Eulerian if and only if it has at most one nontrivial component and its vertices all have even degree. 63 Proof: (Necessity) Also, two edges can be in the same trail only when they lie in the same component, so there is at most one nontrivial component. Component 1 Fundamental Concept Component 2 If more than one components, can’t walk across the graph Graph Theory

Theorem: A graph G is Eulerian if and only if it has at most one nontrivial component and its vertices all have even degree 64 Proof: (Sufficiency 1/3) Assuming that the condition holds, we obtain an Eulerian circuit using induction on the number of edges, m Basis step: m= 0. A closed trail consisting of one vertex suffices Fundamental Concept Graph Theory

Theorem: A graph G is Eulerian if and only if it has at most one nontrivial component and its vertices all have even degree. 65 Proof: (Sufficiency 2/3) Induction step: m>0. When even degrees, each vertex in the nontrivial component of G has degree at least 2. By Lemma 1. 2. 25, the nontrivial component has a cycle C. Let G’ be the graph obtained from G by deleting E(C). Since C has 0 or 2 edges at each vertex, each component of G’ is also an even graph. Since each component is also connected and has fewer than m edges, we can apply the induction hypothesis to conclude that each component of G’ has an Eulerian circuit. Fundamental Concept Graph Theory

Theorem: A graph G is Eulerian if and only if it has at most one nontrivial component and its vertices all have even degree. 66 Proof: (Sufficiency 3/3) Induction step: m>0. (continued) To combine these into an Eulerian circuit of G, we traverse C, but when a component of G’ is entered for the first time we detour along an Eulerian circuit of that component. This circuit ends at the vertex where we began the detour. When we complete the traversal of C, we have completed an Eulerian circuit of G. Fundamental Concept Graph Theory

Proposition: Every even graph decomposes into cycles 67 Proof: In the proof of Theorem 1. 2. 26 It is noted that every even nontrivial graph has a cycle The deletion of a cycle leaves an even graph Thus this proposition follows by induction on the number of edges Fundamental Concept Graph Theory

Proposition: If G is a simple graph in which every vertex has degree at least k, then G contains a path of length at least k. If k 2, then G also contains a cycle of length at least k+1. 68 Proof: (1/2) Let u be an endpoint of a maximal path P in G. Since P does not extend, every neighbor of u is in V(P). Since u has at least k neighbors and G is simple, P therefore has at least k vertices other than u and has length at least k. Fundamental Concept Graph Theory

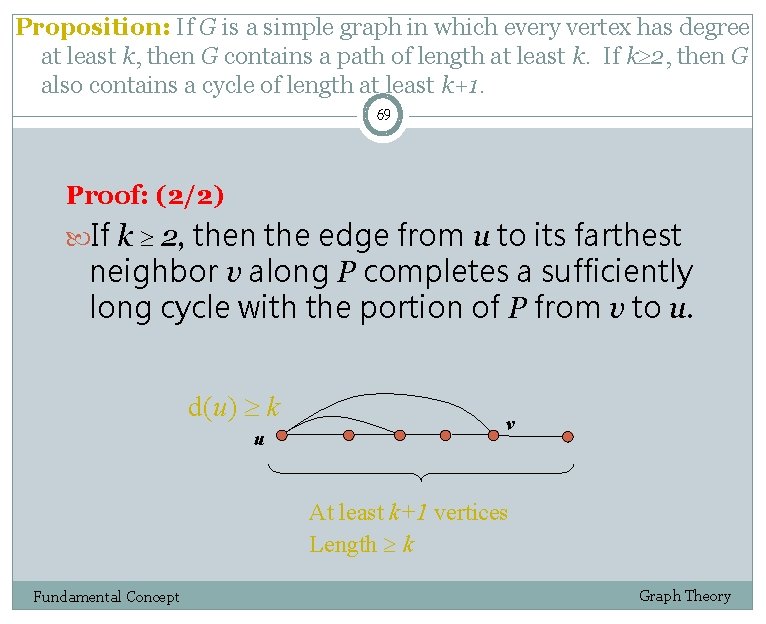
Proposition: If G is a simple graph in which every vertex has degree at least k, then G contains a path of length at least k. If k 2, then G also contains a cycle of length at least k+1. 69 Proof: (2/2) If k 2, then the edge from u to its farthest neighbor v along P completes a sufficiently long cycle with the portion of P from v to u. d(u) k u v At least k+1 vertices Length k Fundamental Concept Graph Theory

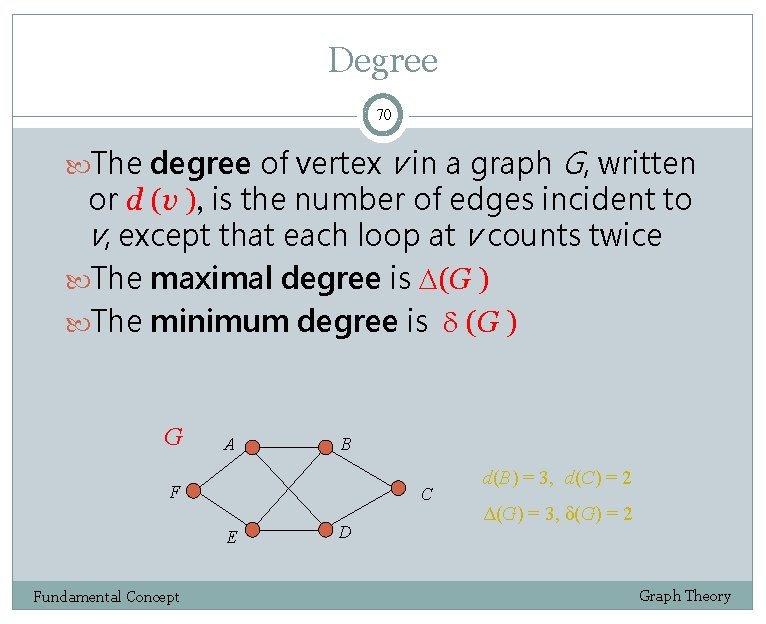
Degree 70 The degree of vertex v in a graph G, written or d (v ), is the number of edges incident to v, except that each loop at v counts twice The maximal degree is (G ) The minimum degree is (G ) G A B F C E Fundamental Concept D d(B) = 3, d(C) = 2 Δ(G) = 3, δ(G) = 2 Graph Theory

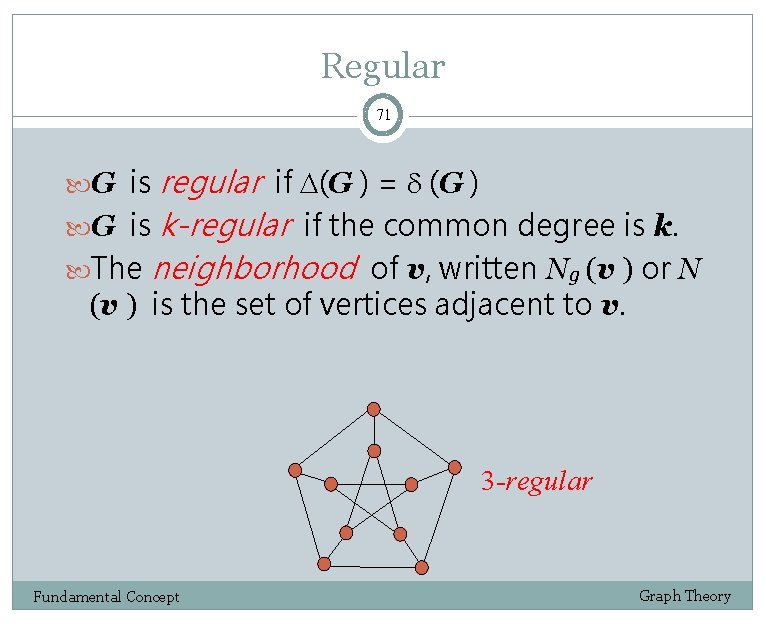
Regular 71 G is regular if (G ) = (G ) G is k-regular if the common degree is k. The neighborhood of v, written Ng (v ) or N (v ) is the set of vertices adjacent to v. 3 -regular Fundamental Concept Graph Theory

Order and size 72 The order of a graph G, written n (G ), is the number of vertices in G. An n-vertex graph is a graph of order n. The size of a graph G, written e (G ), is the number of edges in G. For n N, the notation [n ] indicates the set {1, …, n }. Fundamental Concept Graph Theory

Proposition: (Degree-Sum Formula) If G is a graph, then v V(G)d(v) = 2 e(G) 1. 3. 3 73 Proof: Summing the degrees counts each edge twice, Because each edge has two ends and contributes to the degree at each endpoint. Fundamental Concept Graph Theory

Theorem: If k>0, then a k-regular bipartite graph has the same number of vertices in each partite set. 74 Proof: Let G be an X, Y - bigraph. Counting the edges according to their endpoints in X yields e (G ) = k |X |. d (x) = k Fundamental Concept x Graph Theory

Theorem: If k>0, then a k-regular bipartite graph has the same number of vertices in each partite set. 1. 3. 9 75 Proof: Counting them by their endpoints in Y yields e (G )=k |Y | Thus k |X | = k |Y |, which yields |X |=|Y | when k > 0 d (x) = k Fundamental Concept x y d (y) = k Graph Theory

A technique for counting a set 1/3 1. 3. 10 76 Example: The Petersen graph has ten 6 -cycles Let G be the Petersen graph. Being 3 -regular, G has ten copies of K 1, 3 (claw). We establish a one-to-one correspondence between the 6 -cycles and the claws. Since G has girth 5, every 6 -cycle F is an induced subgraph. see below Each vertex of F has one neighbor outside F. d(v)= 3, v V(G) If Existing, Girth =3. But Girth=5 so no such an edge Fundamental Concept Graph Theory

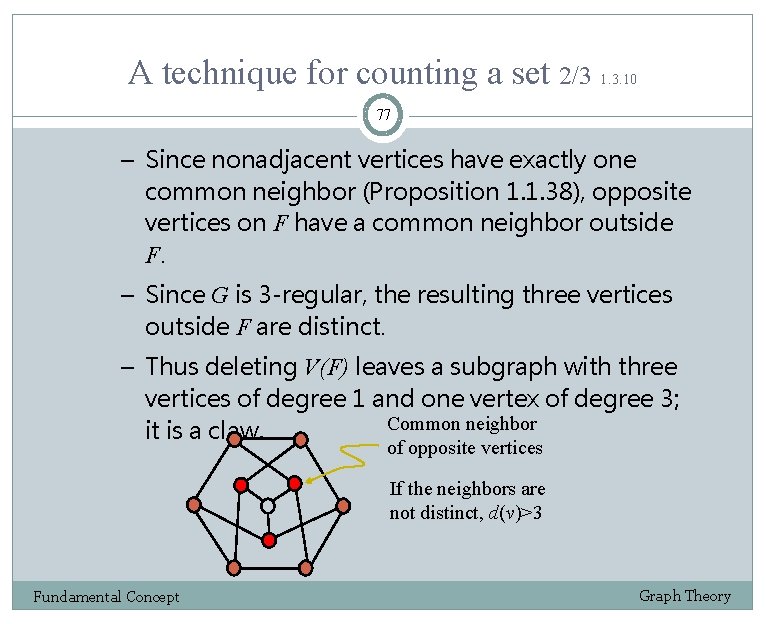
A technique for counting a set 2/3 1. 3. 10 77 – Since nonadjacent vertices have exactly one common neighbor (Proposition 1. 1. 38), opposite vertices on F have a common neighbor outside F. – Since G is 3 -regular, the resulting three vertices outside F are distinct. – Thus deleting V(F) leaves a subgraph with three vertices of degree 1 and one vertex of degree 3; Common neighbor it is a claw. of opposite vertices If the neighbors are not distinct, d(v)>3 Fundamental Concept Graph Theory

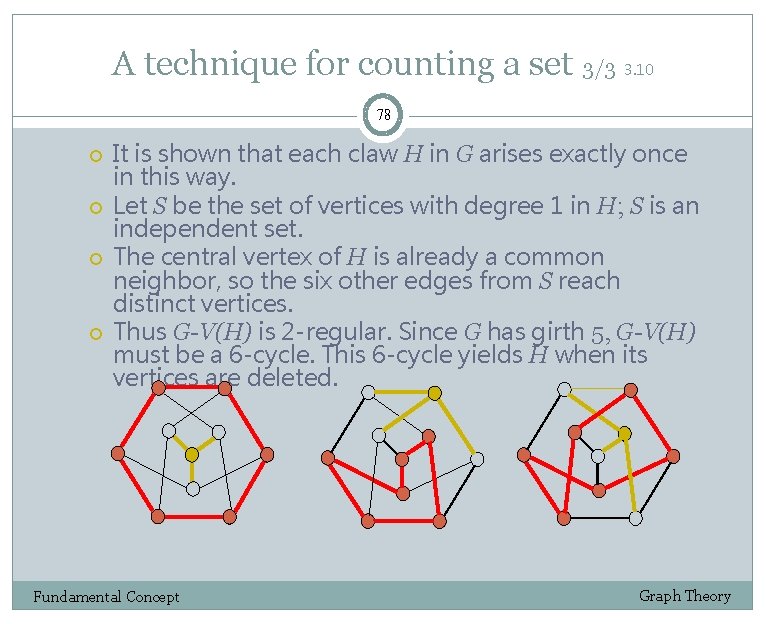
A technique for counting a set 3/3 3. 10 78 It is shown that each claw H in G arises exactly once in this way. Let S be the set of vertices with degree 1 in H; S is an independent set. The central vertex of H is already a common neighbor, so the six other edges from S reach distinct vertices. Thus G-V(H) is 2 -regular. Since G has girth 5, G-V(H) must be a 6 -cycle. This 6 -cycle yields H when its vertices are deleted. Fundamental Concept Graph Theory

Proposition: The minimum number of edges in a connected graph with n vertices is n-1. 3. 13 79 Proof: By proposition 1. 2. 11, every graph with n vertices and k edges has at least n-k components. Hence every n-vertex graph with fewer than n 1 edges has at least two components and is disconnected. The contrapositive of this is that every connected n-vertex graph has at least n-1 edges. This lower bound is achieved by the path Pn. Fundamental Concept Graph Theory

Theorem: If G is simple n-vertex graph with (G) (n-1)/2, then G is connected. 1. 3. 15 80 Proof: 1/2 Choose u, v V (G ). It suffices to show that u, v have a common neighbor if they are not adjacent. Since G is simple, we have |N(u) | (G ) (n-1)/2, and similarly for v. Recall: (G ) is the minimum degree, |N(u)| = d(u) Hence: |N(u) | (G ) Fundamental Concept Graph Theory

Theorem: If G is simple n-vertex graph with (G) (n-1)/2, then G is connected. 1. 3. 15 81 Proof: 2/2 When u and v are not connected, we have |N(u ) N(v )| n - 2 since u and v are not in the union Using Remark A. 13 of Appendix A, we thus compute Fundamental Concept Graph Theory

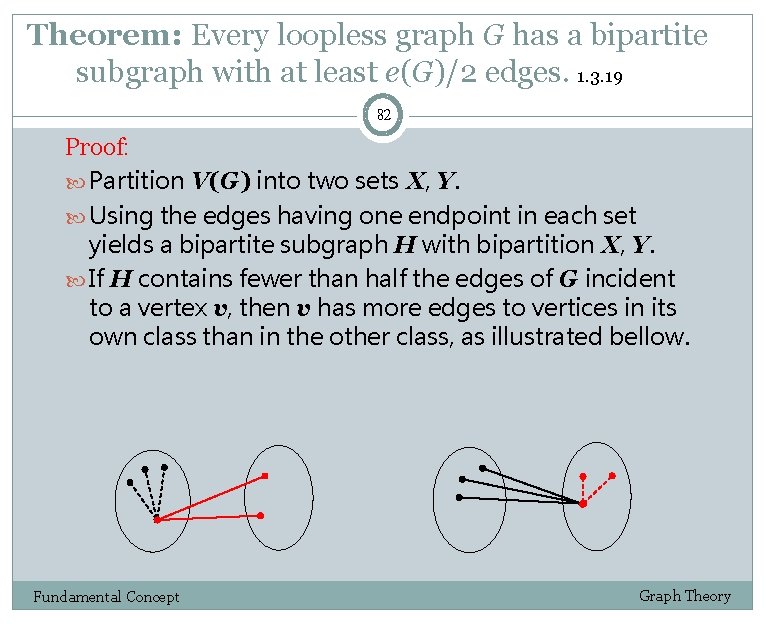
Theorem: Every loopless graph G has a bipartite subgraph with at least e(G)/2 edges. 1. 3. 19 82 Proof: Partition V(G) into two sets X, Y. Using the edges having one endpoint in each set yields a bipartite subgraph H with bipartition X, Y. If H contains fewer than half the edges of G incident to a vertex v, then v has more edges to vertices in its own class than in the other class, as illustrated bellow. Fundamental Concept Graph Theory

Theorem: Every loopless graph G has a bipartite subgraph with at least e(G)/2 edges. 1. 3. 19 83 Proof: 2/2 Moving v to the other class gains more edges of G than it loses. Using Iterative improvement approach When it terminates, we have d. H(v) d. G(v)/2 for every v V(G). Summing this and applying the degree-sum formula yields e(H) e(G)/2. Fundamental Concept Graph Theory

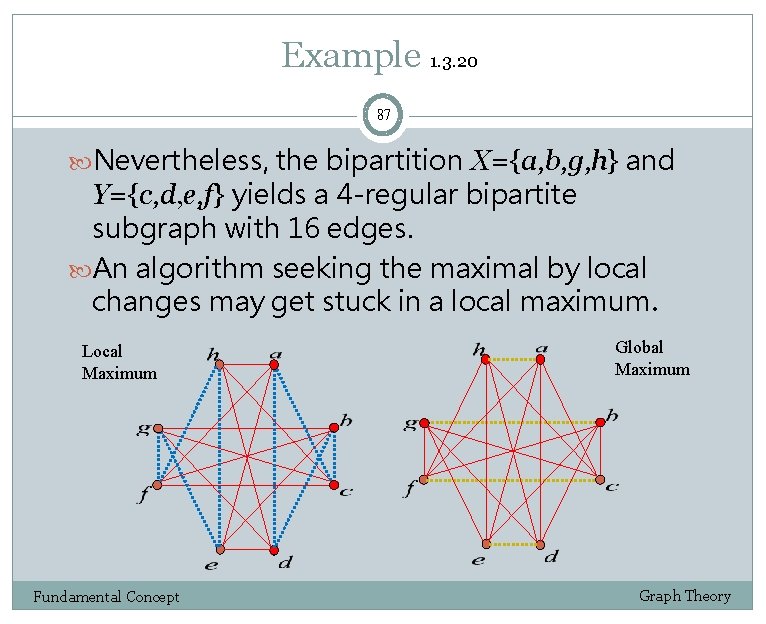
Example 1 1. 3. 20 84 The algorithm in Theorem 1. 3. 19 need not produce a bipartite subgraph with the most edges, merely one with at least half the edges Local Maximum Fundamental Concept Graph Theory

Example 2 1. 3. 20 85 Consider the graph in the next page. It is 5 -regular with 8 vertices and hence has 20 edges. The bipartition X={a, b, c, d} and Y={e, f, g, h} yields a 3 -regular bipartite subgraph with 12 edges. The algorithm terminates here: switching one vertex would pick up two edges but lose three. Fundamental Concept Graph Theory

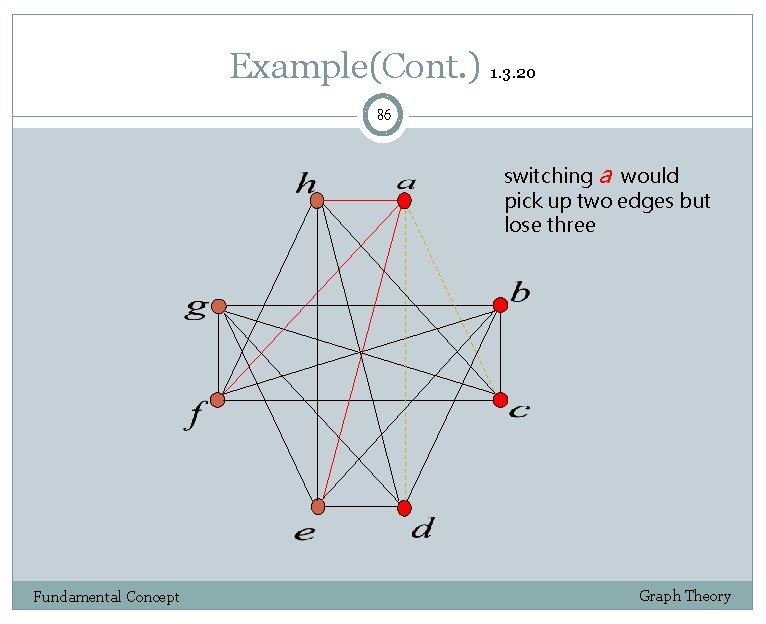
Example(Cont. ) 1. 3. 20 86 switching a would pick up two edges but lose three Fundamental Concept Graph Theory

Example 1. 3. 20 87 Nevertheless, the bipartition X={a, b, g, h} and Y={c, d, e, f} yields a 4 -regular bipartite subgraph with 16 edges. An algorithm seeking the maximal by local changes may get stuck in a local maximum. Local Maximum Fundamental Concept Global Maximum Graph Theory

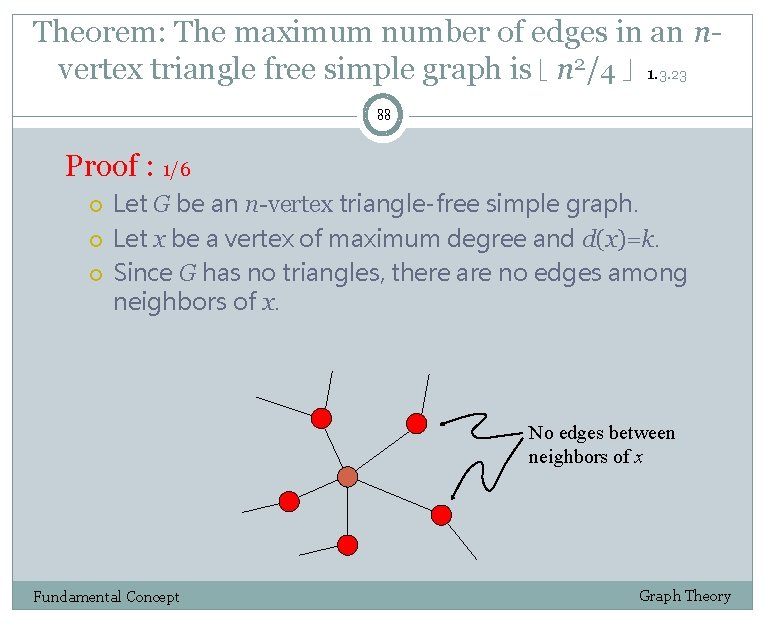
Theorem: The maximum number of edges in an nvertex triangle free simple graph is n 2/4 1. 3. 23 88 Proof : 1/6 Let G be an n-vertex triangle-free simple graph. Let x be a vertex of maximum degree and d(x)=k. Since G has no triangles, there are no edges among neighbors of x. No edges between neighbors of x Fundamental Concept Graph Theory

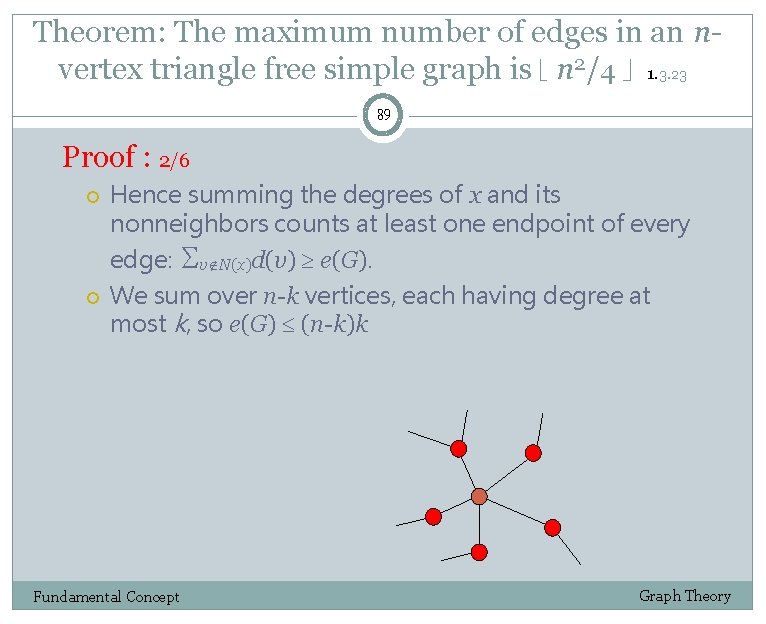
Theorem: The maximum number of edges in an nvertex triangle free simple graph is n 2/4 1. 3. 23 89 Proof : 2/6 Hence summing the degrees of x and its nonneighbors counts at least one endpoint of every edge: v N(x)d(v) e(G). We sum over n-k vertices, each having degree at most k, so e(G) (n-k)k Fundamental Concept Graph Theory

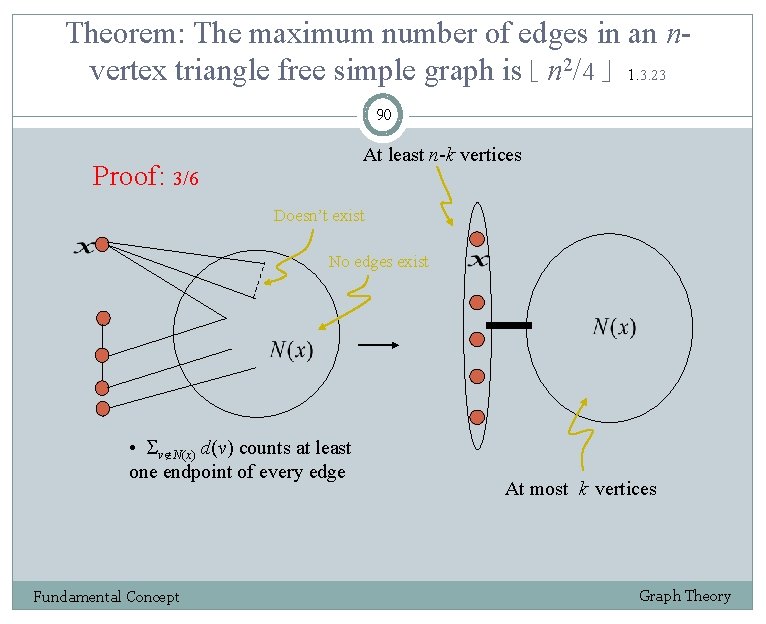
Theorem: The maximum number of edges in an nvertex triangle free simple graph is n 2/4 1. 3. 23 90 At least n-k vertices Proof: 3/6 Doesn’t exist No edges exist • v N(x) d(v) counts at least one endpoint of every edge Fundamental Concept At most k vertices Graph Theory

Theorem: The maximum number of edges in an n-vertex triangle free simple graph is n 2/4 1. 3. 23 91 Proof: 4/6 Since (n-k)k counts the edges in Kn-k, k, we have now proved that e(G) is bounded by the size of some biclique with n vertices. i. e. e(G) (n-k)k = |the edges in Kn-k, k | n-k Fundamental Concept k Graph Theory

Theorem: The maximum number of edges in an nvertex triangle free simple graph is n 2/4 1. 3. 23 92 Proof: 5/6 – Moving a vertex of Kn-k, k from the set of size k to the set of size n-k gains k-1 edges and loses n-k edges. – The net gain is 2 k-1 -n, which is positive for 2 k>n+1 and negative for 2 k<n+1. – Thus e(Kn-k, k) is maximized when k is n/2 or n/2 . n-k Fundamental Concept k Graph Theory

Theorem: The maximum number of edges in an nvertex triangle free simple graph is n 2/4 1. 3. 23 93 Proof: 6/6 The product is then n 2/4 for even n and (n 2 -1)/4 for odd n. Thus e(G) n 2/4 . The bound is best possible. Fundamental Concept It is seen that a triangle-free graph with n 2/4 edges is: K n/2 , n/2 . Graph Theory

Degree sequence 1. 3. 27 94 The Degree Sequence of a graph is the list of vertex degrees, usually written in nonincreasing order, as d 1 …. d n. Example: x v w y Degree sequence: d(w), d(x), d(y), d(z), d(v) z Fundamental Concept Graph Theory

Proposition: The nonnegative integers d 1 , …, dn are the vertex degrees of some graph if and only if di is even. 1. 3. 28 95 Proof: ½ Necessity When some graph G has these numbers as its vertex degrees, the degree-sum formula implies that di = 2 e (G), which is even. Fundamental Concept Graph Theory

Proposition: The nonnegative integers d 1 , …, dn are the vertex degrees of some graph if and only if di is even. 1. 3. 28 96 Proof: 2/2 Sufficiency Suppose that di is even. We construct a graph with vertex set v 1, …, vn and d(vi) = di for all i. Since di is even, the number of odd values is even. First form an arbitrary pairing of the vertices in {vi : di is odd}. For each resulting pair, form an edge having these two vertices as its endpoints The remaining degree needed at each vertex is even and nonnegative; satisfy this for each i by placing [di /2] loops at vi Fundamental Concept Graph Theory

Graphic Sequence 1. 3. 29 97 A graphic sequence is a list of nonnegative numbers that is the degree sequence of some simple graph. A simple graph “realizes” d. means: A simple graph with degree sequence d. Fundamental Concept Graph Theory

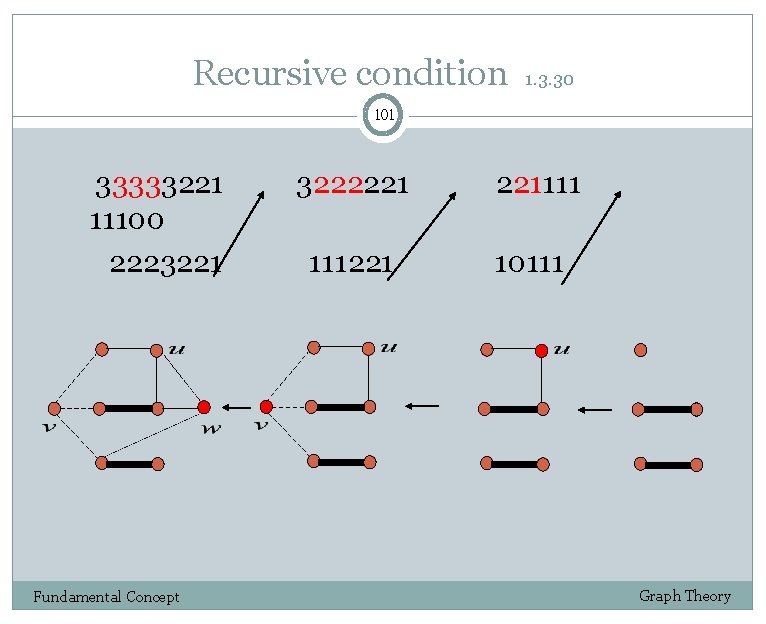
Recursive condition 1. 3. 30 98 The lists (2, 2, 1, 1) and (1, 0, 1) are graphic. The graphic K 2+K 1 realizes 1, 0, 1. Adding a new vertex adjacent to vertices of degrees 1 and 0 yields a graph with degree sequence 2, 2, 1, 1, as shown below. Conversely, if a graph realizing 2, 2, 1, 1 has a vertex w with neighbors of degrees 2 and 1, then deleting w yields a graph with degrees 1, 0, 1. 2 1 K 2 Fundamental Concept 1 2 0 K 1 1 1 Graph Theory

Recursive condition 1. 3. 30 99 Similarly, to test 33333221, we seek a realization with a vertex w of degree 3 having three neighbors of degree 3. Delete this Vertex A new degree sequence Fundamental Concept 33333221 2223221 Graph Theory

Recursive condition 1. 3. 30 100 This exists if and only if 2223221 is graphic. (See next page) We reorder this and test 3222221. We continue deleting and reordering until we can tell whether the remaining list is realizable. If it is, then we insert vertices with the desired neighbors to walk back to a realization of the original list. The realization is not unique. The next theorem implies that this recursive test works. Fundamental Concept Graph Theory

Recursive condition 1. 3. 30 101 33333221 11100 2223221 Fundamental Concept 3222221 221111 111221 10111 Graph Theory

Theorem. For n>1, an integer list d of size n is graphic if and only if d’ is graphic, where d’ is obtained from d by deleting its largest element and subtracting 1 from its next largest elements. The only 1 -element graphic sequence is d 1=0. 1. 3. 31 102 Proof: 1/6 For n =1, the statement is trivial. For n >1, we first prove that the condition is sufficient. Give d with d 1 …. . dn and a simple graph G’ with degree sequence d’ For Example: We have: 1) d = 33333221 2) G’ with d’ = 2223221 G’ We show: d is graphic Fundamental Concept Graph Theory

Theorem. For n>1, an integer list d of size n is graphic if and only if d’ is graphic, where d’ is obtained from d by deleting its largest element and subtracting 1 from its next largest elements. The only 1 -element graphic sequence is d 1=0. 1. 3. 31 103 Proof: 2/6 We add a new vertex adjacent to vertices in G’ with degrees d 2 -1, …. . , d +1 -1. These di are the largest elements of d after (one copy of) itself, Note : d 2 -1, …. . , d +1 -1 need not be the largest numbers in d’ (see example in previous page) G’ d : d 1, d 2, … dn d’ : d 2 -1, …. . , d +1 -1, … dn New added vertex Fundamental Concept May not be the largest numbers Graph Theory

Theorem 1. 3. 31 continue 104 To prove necessity, 3/6 Given a simple graph G realizing d , we produce a simple graph G’ realizing d’ Let w be a vertex of degree in G, and let S be a set of vertices in G having the “desired degrees” d 2, …. . , d +1 w d : d 1, d 2, …d , d +1, … dn d 1= Fundamental Concept S: vertices Graph Theory

Theorem 1. 3. 31 105 Proof: continue 4/6 If N(w)=S, then we delete w to obtain G’. w d : d 1, d 2, …d , d +1, … dn d 1= Vertices, N(w)=S i. e. They are connected to w Delete w than we have d’ : d 2 -1, …. . , d +1 -1, … dn Fundamental Concept Graph Theory

Theorem 1. 3. 31 106 Proof: continue Otherwise, 5/6 Some vertex of S is missing from N(w). In this case, we modify G to increase |N(w) S| without changing any vertex degree. Since |N(w) S| can increase at most times, repeating this converts G into another graph G* that realizes d and has S as the neighborhood of w. From G* we then delete w to obtain the desired graph G’ realizing d’. w d : d 1, d 2, …d , d +1, … dn d 1= Fundamental Concept Vertices, N(w) S i. e. Some vertices are not connected to w. - We make them become connected to w without changing their degree. Graph Theory

Theorem 1. 3. 31 107 Proof: continue 6/6 To find the modification when N(w) S , we choose x S and z S so that w z are connected and w x are not. We want to add wx and delete wz, but we must preserve vertex degrees. Since d(x)>d(z) and already w is a neighbor of z but not x, there must be a vertex y adjacent to x but not to z. Now we delete {wz, xy} and add {wx, yz} to increase |N(w) S|. w z y x This y must exist. Fundamental Concept w z y x It becomes connected w Graph Theory

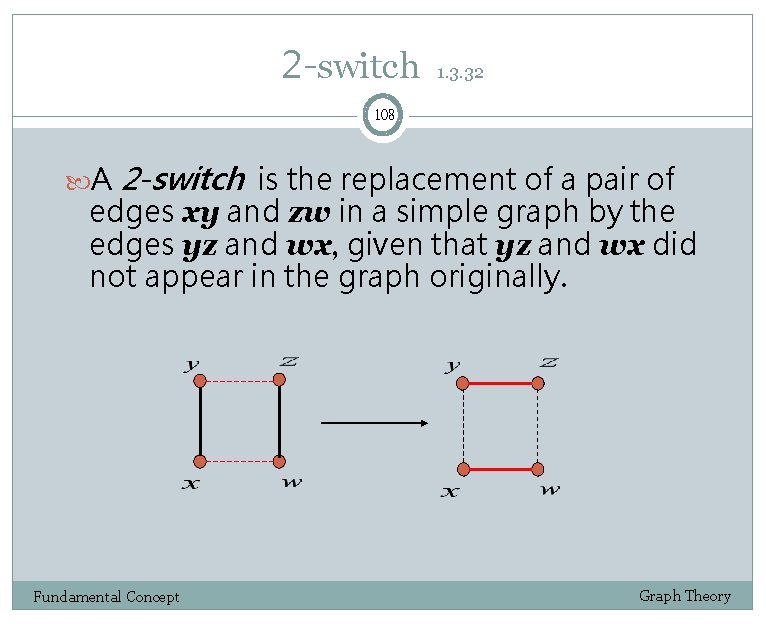
2 -switch 1. 3. 32 108 A 2 -switch is the replacement of a pair of edges xy and zw in a simple graph by the edges yz and wx, given that yz and wx did not appear in the graph originally. Fundamental Concept Graph Theory

Theorem: If G and H are two simple graphs with vertex set V, then d. G(v)=d. H(v) for every v V if and only if there is a sequence of 2 switches that transforms G into H. 1. 3. 33 109 Proof: Every 2 -switch preserves vertex degrees, so the condition is sufficient. Conversely, when d. G(v)=d. H(v) for all v V , we obtain an appropriate sequence of 2 -switches by induction on the number of vertices, n. If n<3, then for each d 1, …. . , dn there is at most one simple graph with d(vi)=di. Hence we can use n=3 as the basis step. Fundamental Concept Graph Theory

Theorem. 1. 3. 33 (Continue) 110 Consider n 4 , and let w be a vertex of maximum degree, Let S={v 1, …. . , v } be a fixed set of vertices with the highest degrees other than w As in the proof of Theorem 1. 3. 31, some sequence of 2 -switches transforms G to a graph G* such that NG*(w)=S, and some such sequence transforms H to a graph H* such that NH*(w)=S Since NG*(w)=NH*(w), deleting w leaves simple graphs G’=G*-w and H’=H*-w with d. G’(v)=d. H’(v) for every vertex v Fundamental Concept Graph Theory

Theorem. 1. 3. 33 Continue 111 By the induction hypothesis, some sequence of 2 - switches transforms G’ to H’. Since these do not involve w, and w has the same neighbors in G* and H*, applying this sequence transforms G* to H*. Hence we can transform G to H by transforming G to G*, then G* to H*, then (in reverse order) the transformation of H to H*. Fundamental Concept Graph Theory

Directed Graph and Its edges 1. 4. 2 112 A directed graph or digraph G is a triple: A vertex set V(G), An edge set E(G), and A function assigning each edge an ordered pair of vertices. The first vertex of the ordered pair is the tail of the edge The second is the head Together, they are the endpoints. An edge is said to be from its tail to its head. The terms “head” and “tail” come from the arrows used to draw digraphs. Fundamental Concept Graph Theory

Directed Graph and its edges 1. 4. 2 113 As with graphs, we assign each vertex a point in the plane and each edge a curve joining its endpoints. When drawing a digraph, we give the curve a direction from the tail to the head. Fundamental Concept Graph Theory

Directed Graph and its edges 1. 4. 2 114 When a digraph models a relation, each ordered pair is the (head, tail) pair for at most one edge. In this setting as with simple graphs, we ignore the technicality of a function assigning endpoints to edges and simply treat an edge as an ordered pair of vertices. Fundamental Concept Graph Theory

Loop and multiple edges in directed graph 1. 4. 3 115 In a graph, a loop is an edge whose endpoints are equal. Multiple edges are edges having the same ordered pair of endpoints. A digraph is simple if each ordered pair is the head and tail of the most one edge; one loop may be present at each vertex. Loop Fundamental Concept Multiple edges Graph Theory

Loop and multiple edges in directed graph 1. 4. 3 116 In the simple digraph, we write uv for an edge with tail u and head v. If there is an edge form u to v, then v is a successor of u, and u is a predecessor of v. We write u v for “there is an edge from u to v”. Predecessor Successor Fundamental Concept Graph Theory

Path and Cycle in Digraph 1. 4. 6 117 A digraph is a path if it is a simple digraph whose vertices can be linearly ordered so that there is an edge with tail u and head v if and only if v immediately follows u in the vertex ordering. A cycle is defined similarly using an ordering of the vertices on the cycle. Fundamental Concept Graph Theory

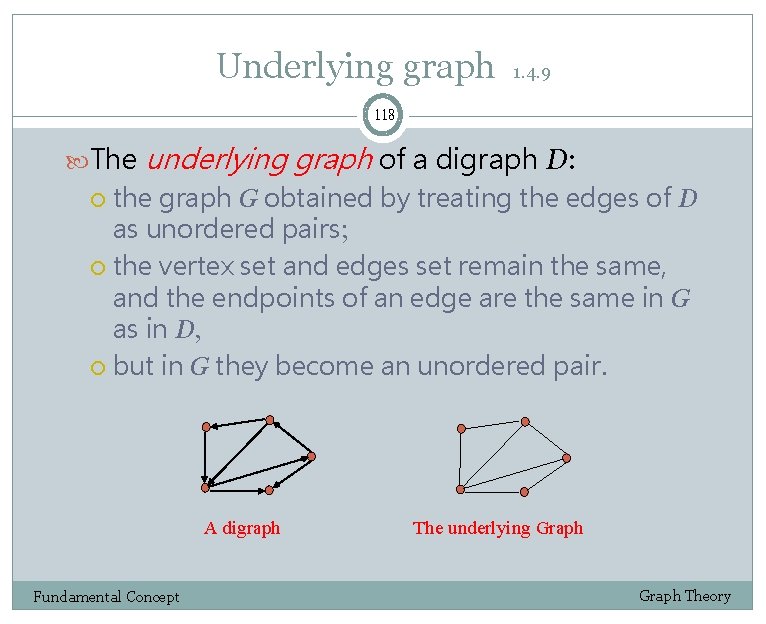
Underlying graph 1. 4. 9 118 The underlying graph of a digraph D: the graph G obtained by treating the edges of D as unordered pairs; the vertex set and edges set remain the same, and the endpoints of an edge are the same in G as in D, but in G they become an unordered pair. A digraph Fundamental Concept The underlying Graph Theory

Underlying graph 1. 4. 9 119 Most ideals and methods of graph theorem arise in the study of ordinary graphs. Digraphs can be a useful additional tool, especially in applications When comparing a digraph with a graph, we usually use G for the graph and D for the digraph. When discussing a single digraph, we often use G. Fundamental Concept Graph Theory

Adjacency Matrix and Incidence Matrix of a Digraph 1. 4. 10 120 In the adjacency matrix A(G) of a digraph G, the entry in position i, j is the number of edges from vi to vj. In the incidence matrix M(G) of a loopless digraph G, we set mi, j=+1 if vi is the tail of ej and mi, j= -1 if vi is the head of ej. Fundamental Concept Graph Theory

Example of adjacency matrix 1. 4. 11 121 The underlying graph of the digraph below is the graph of Example 1. 1. 19; note the similarities and differences in their matrices. Fundamental Concept Graph Theory

Connected Digraph 1. 4. 12 122 To define connected digraphs, two options come to mind. We could require only that the underlying graph be connected. However, this does not capture the most useful sense of connection for digraphs. Fundamental Concept Graph Theory

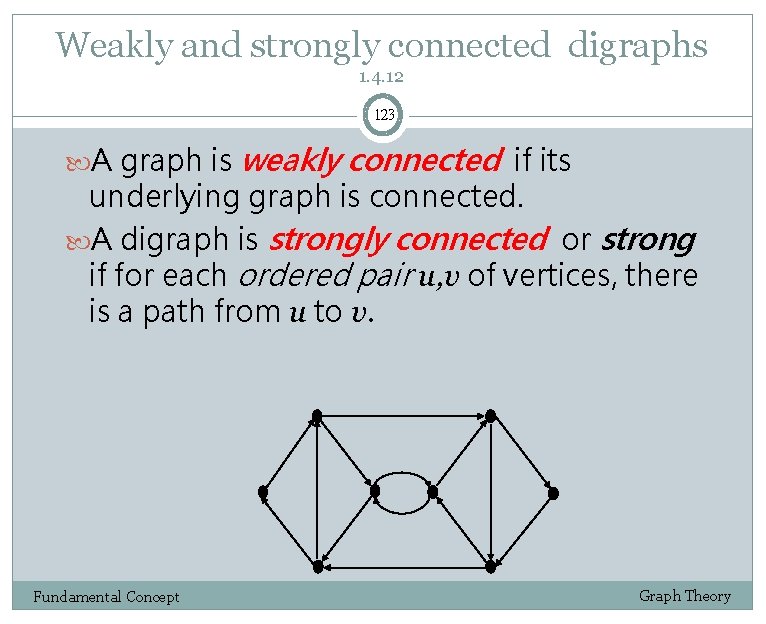
Weakly and strongly connected digraphs 1. 4. 12 123 A graph is weakly connected if its underlying graph is connected. A digraph is strongly connected or strong if for each ordered pair u, v of vertices, there is a path from u to v. Fundamental Concept Graph Theory

Eulerian Digraph 1. 4. 22 124 An Eulerian trail in digraph (or graph) is a trail containing all edges. An Eulerian circuit is a closed trail containing all edges. A digraph is Eulerian if it has an Eulerian circuit. Fundamental Concept Graph Theory

Lemma. If G is a digraph with +(G) 1, then G contains a cycle. The same conclusion holds when -(G) 1. 1. 4. 23 125 Proof. Let P be a maximal path in G, and u be the last vertex of P. Since P cannot be extended, every successor of u must already be a vertex of P. Since +(G) 1, u has a successor v on P. The edge uv completes a cycle with the portion of P from v to u. Fundamental Concept Graph Theory

126 Theorem: A digraph is Eulerian if and only if d+(v)=d-(v) for each vertex v and the underlying graph has at most one nontrivial component. 1. 4. 24 Fundamental Concept Graph Theory

De Bruijn cycles 1. 4. 25 127 Application: There are 2 n binary strings of length n. Is there a cyclic arrangement of 2 n binary digits such that the 2 n strings of n consecutive digitals are all distinct? Example: For n =4, (0000111101100101) works. 0000 0001 0011 0111 1110 1101 1011 … 1 0 0 1 1 Fundamental Concept 0 1 1 Graph Theory

De Bruijn cycles 1. 4. 25 128 We can use such an arrangement to keep track of the position of a rotating drum. One drum has 2 n rotational positions. A band around the circumference is split into 2 n portions that can be coded 0 or 1. Sensors read n consecutive portions. If the coding has the property specified above, then the position of the drum is determined by the string read by the sensors. Fundamental Concept Graph Theory

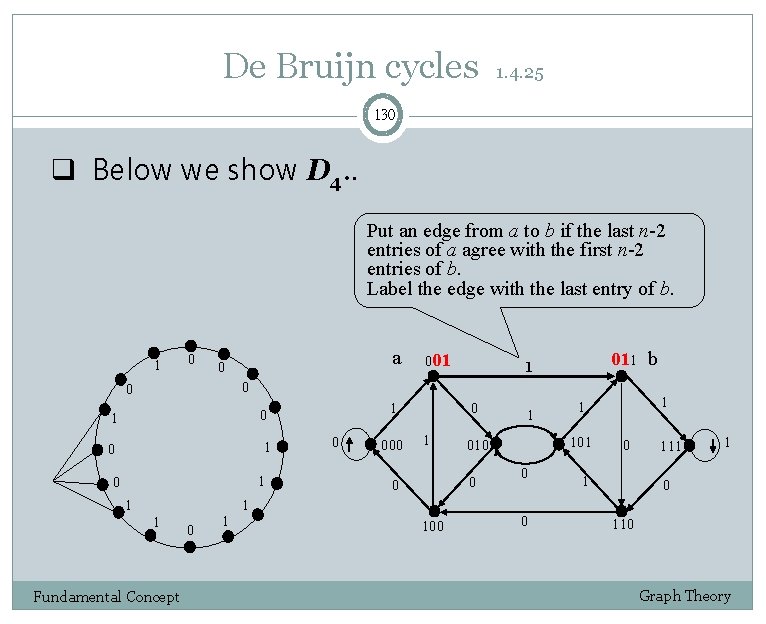
De Bruijn cycles 1. 4. 25 129 To obtain such a circular arrangement, define a digraph Dn whose vertices are the binary (n 1)-tuples. Put an edge from a to b if the last n-2 entries of a agree with the first n-2 entries of b. Label the edge with the last entry of b. Fundamental Concept Graph Theory

De Bruijn cycles 1. 4. 25 130 q Below we show D 4. . Put an edge from a to b if the last n-2 entries of a agree with the first n-2 entries of b. Label the edge with the last entry of b. 1 0 a 0 001 011 b 1 0 0 1 1 Fundamental Concept 0 1 1 0 000 0 1 1 100 0 0 1 1 101 010 0 0 1 111 1 0 110 Graph Theory

De Bruijn cycles 1. 4. 25 131 q We next prove that Dn is Eulerian and show an Eulerian circuit yields the desired circular arrangement. Fundamental Concept Graph Theory

Theorem. The digraph Dn of Application 1. 4. 25 is Eulerian, and the edge labels on the edges in any Eulerian circuit of Dn form a cyclic arrangement in which the 2 n consecutive segments of length n are distinct. 1. 4. 26 132 Proof: We show first that Dn is Eulerian. Then the labels on the edges in any Eulerian circuit of Dn form a cyclic arrangement in which the 2 n consecutive segments of length n are distinct. Fundamental Concept Graph Theory

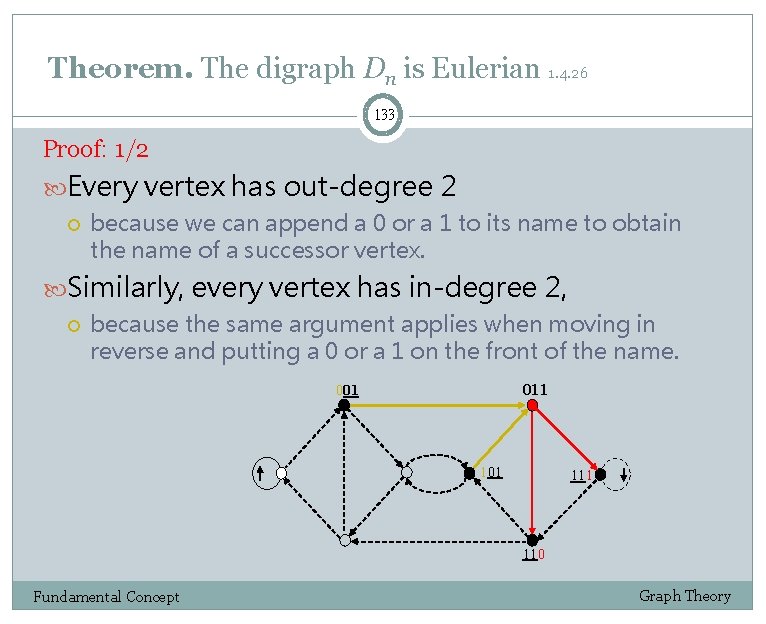
Theorem. The digraph Dn is Eulerian 1. 4. 26 133 Proof: 1/2 Every vertex has out-degree 2 because we can append a 0 or a 1 to its name to obtain the name of a successor vertex. Similarly, every vertex has in-degree 2, because the same argument applies when moving in reverse and putting a 0 or a 1 on the front of the name. 011 001 111 110 Fundamental Concept Graph Theory

Theorem. The digraph Dn is Eulerian 1. 4. 26 134 Proof: 2/2 Also, Dn is strongly connected, because we can reach the vertex b=(b 1, …. . , bn-1) from any vertex by successively follows the edges labeled b 1, …. . , bn-1. Thus Dn satisfies the hypotheses of Theorem 1. 4. 24 and is Eulerian. a 001 1 0 000 0 1 1 100 Fundamental Concept 1 0 0 1 1 101 010 0 0 011 b 1 0 1 111 1 0 110 Graph Theory

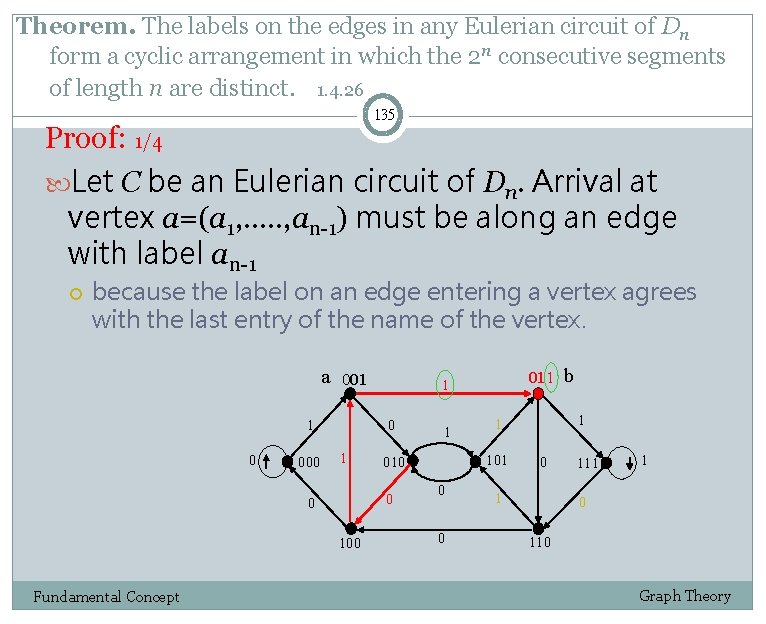
Theorem. The labels on the edges in any Eulerian circuit of Dn form a cyclic arrangement in which the 2 n consecutive segments of length n are distinct. 1. 4. 26 135 Proof: 1/4 Let C be an Eulerian circuit of Dn. Arrival at vertex a=(a 1, …. . , an-1) must be along an edge with label an-1 because the label on an edge entering a vertex agrees with the last entry of the name of the vertex. a 001 1 0 000 0 1 100 Fundamental Concept 1 0 0 1 1 101 010 0 0 011 b 1 0 1 111 1 0 110 Graph Theory

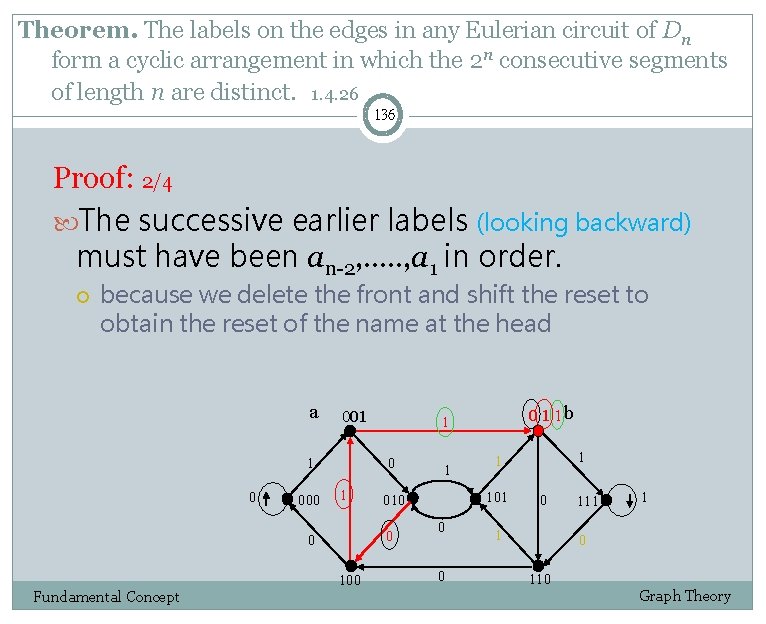
Theorem. The labels on the edges in any Eulerian circuit of Dn form a cyclic arrangement in which the 2 n consecutive segments of length n are distinct. 1. 4. 26 136 Proof: 2/4 The successive earlier labels (looking backward) must have been an-2, …. . , a 1 in order. because we delete the front and shift the reset to obtain the reset of the name at the head a 001 1 0 000 0 1 Fundamental Concept 100 1 0 0 1 1 101 010 0 1 1 b 1 0 1 111 1 0 110 Graph Theory

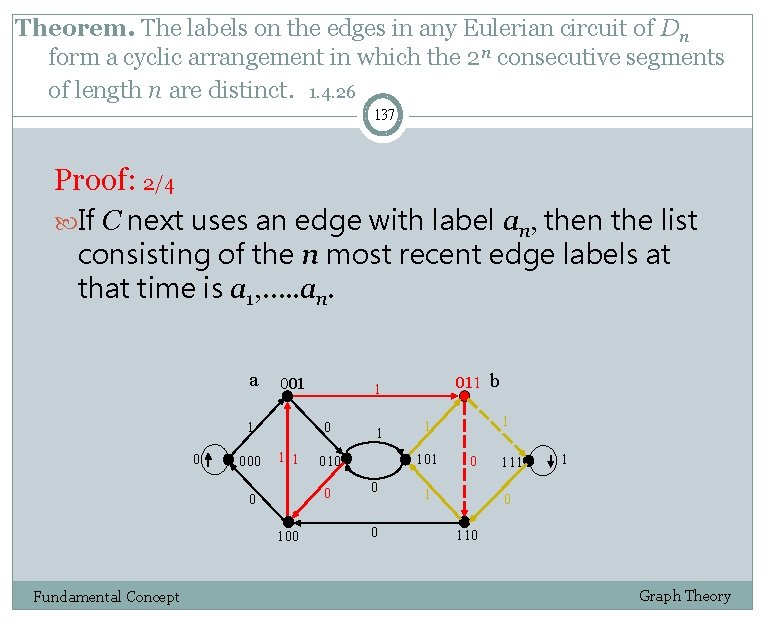
Theorem. The labels on the edges in any Eulerian circuit of Dn form a cyclic arrangement in which the 2 n consecutive segments of length n are distinct. 1. 4. 26 137 Proof: 2/4 If C next uses an edge with label an, then the list consisting of the n most recent edge labels at that time is a 1, …. . an. a 001 1 0 000 0 1 1 100 Fundamental Concept 1 0 0 1 1 101 010 0 0 011 b 1 0 1 111 1 0 110 Graph Theory

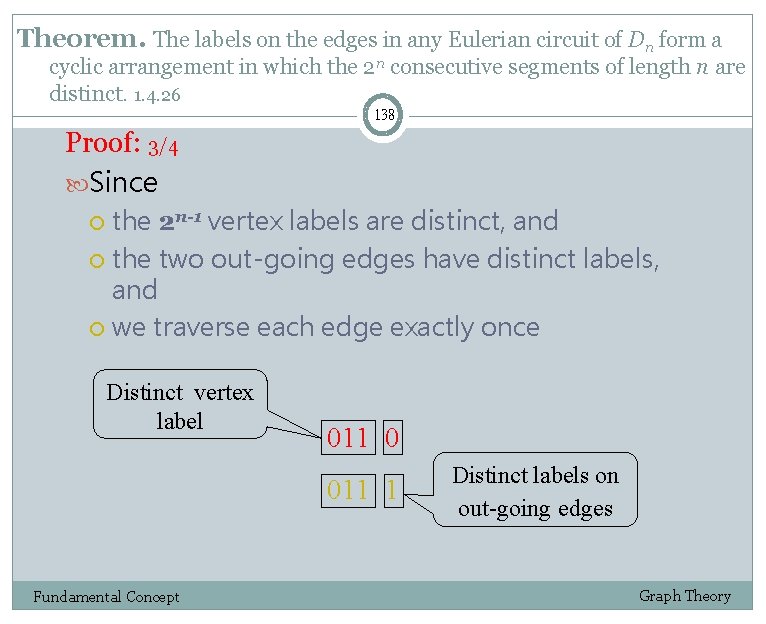
Theorem. The labels on the edges in any Eulerian circuit of Dn form a cyclic arrangement in which the 2 n consecutive segments of length n are distinct. 1. 4. 26 138 Proof: 3/4 Since the 2 n-1 vertex labels are distinct, and the two out-going edges have distinct labels, and we traverse each edge exactly once Distinct vertex label 011 0 011 1 Fundamental Concept Distinct labels on out-going edges Graph Theory

Theorem. The labels on the edges in any Eulerian circuit of Dn form a cyclic arrangement in which the 2 n consecutive segments of length n are distinct. 1. 4. 26 139 Proof: 4/4 We have shown that the 2 n strings of length n in the circular arrangement given by the edge labels along C are distinct. Fundamental Concept Graph Theory