Graph Sparsifiers A Survey Nick Harvey UBC Based

Graph Sparsifiers: A Survey Nick Harvey UBC Based on work by: Batson, Benczur, de Carli Silva, Fung, Hariharan, Harvey, Karger, Panigrahi, Sato, Spielman, Srivastava and Teng

Approximating Dense Objects by Sparse Ones • Floor joists • Image compression

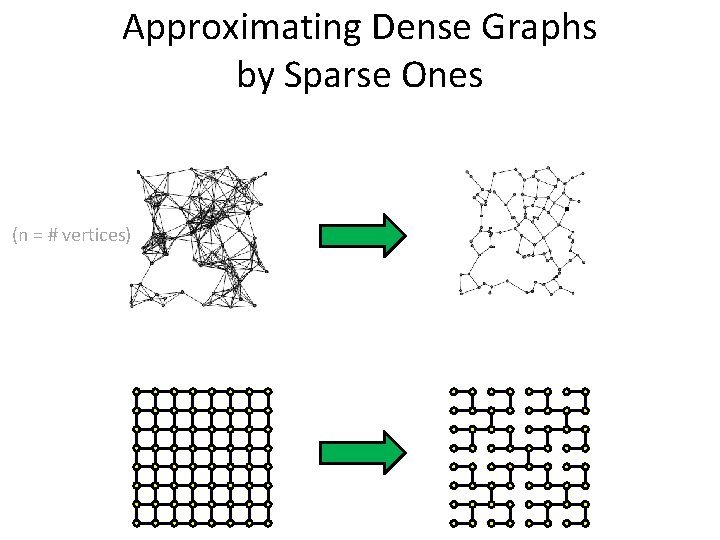
Approximating Dense Graphs by Sparse Ones (n = # vertices)

Overview • Definitions – Cut & Spectral Sparsifiers – Applications • Cut Sparsifiers • Spectral Sparsifiers – A random sampling construction – Derandomization

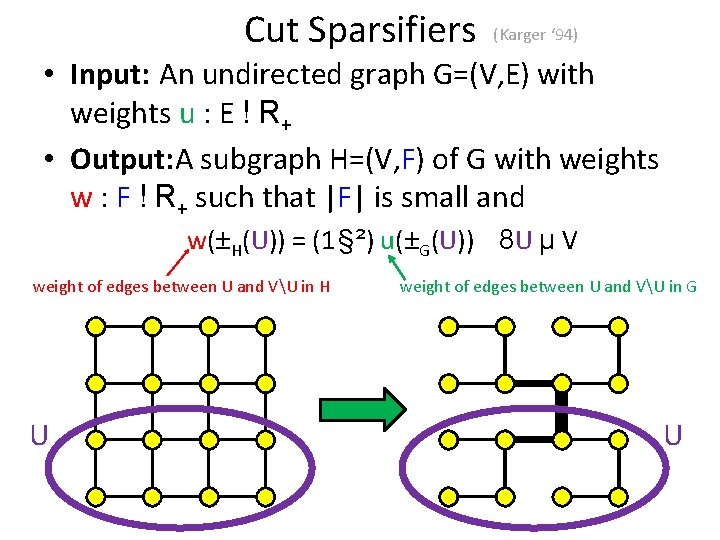
Cut Sparsifiers (Karger ‘ 94) • Input: An undirected graph G=(V, E) with weights u : E ! R+ • Output: A subgraph H=(V, F) of G with weights w : F ! R+ such that |F| is small and w(±H(U)) = (1 § ²) u(±G(U)) 8 U µ V weight of edges between U and VU in H U weight of edges between U and VU in G U

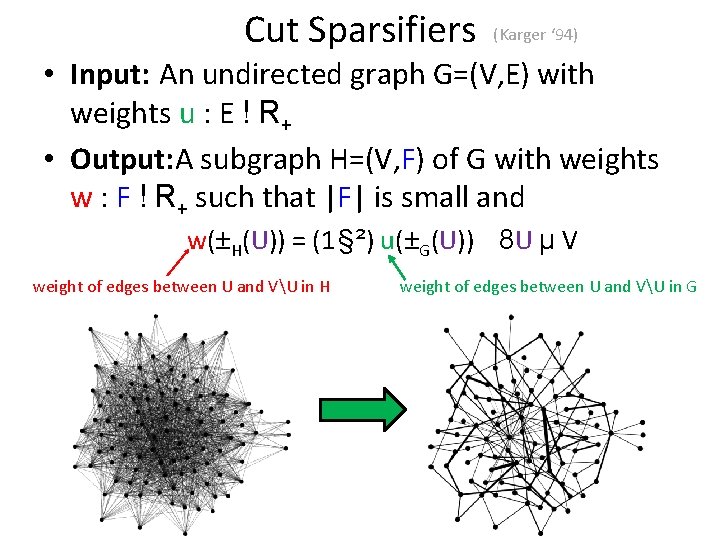
Cut Sparsifiers (Karger ‘ 94) • Input: An undirected graph G=(V, E) with weights u : E ! R+ • Output: A subgraph H=(V, F) of G with weights w : F ! R+ such that |F| is small and w(±H(U)) = (1 § ²) u(±G(U)) 8 U µ V weight of edges between U and VU in H weight of edges between U and VU in G

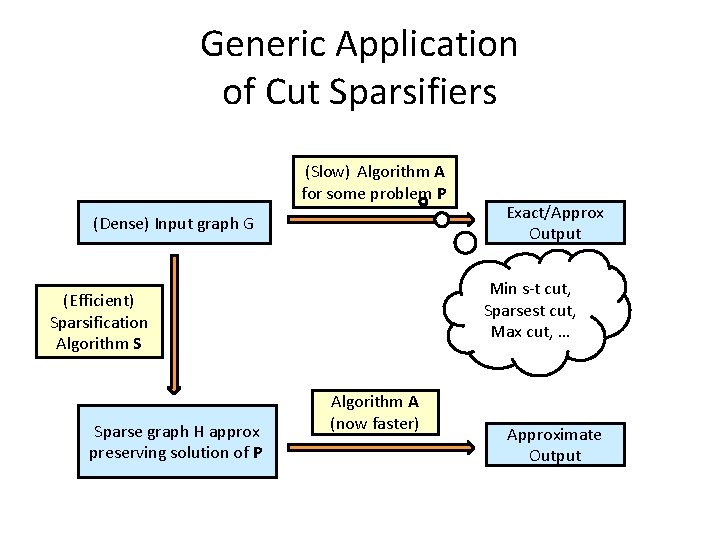
Generic Application of Cut Sparsifiers (Slow) Algorithm A for some problem P (Dense) Input graph G Min s-t cut, Sparsest cut, Max cut, … (Efficient) Sparsification Algorithm S Sparse graph H approx preserving solution of P Exact/Approx Output Algorithm A (now faster) Approximate Output

Relation to Expander Graphs G H

Relation to Expander Graphs • Simple Random Construction: Erdos-Renyi graph Gnp is an expander if p=£(log(n)/n), with high probability. This gives an expander with £(n log n) edges with high probability. But aren’t there much better expanders? G H

Spectral Sparsifiers (Spielman-Teng ‘ 04)

Spectral Sparsifiers (Spielman-Teng ‘ 04) • Input: An undirected graph G=(V, E) with weights u : E ! R+ • Def: The Laplacian is the matrix LG such that x. T LG x = st 2 E ust (xs-xt)2 8 x 2 RV. • Output: A subgraph H=(V, F) of G with weights w : F ! R such that |F| is small and x. T LH x = (1 § ²) x. T LG x 8 x 2 RV w(±H(U)) = (1 § ²) u(±G(U)) 8 U µ V ) ) Restrict to {0, 1}-vectors Spectral Sparsifier Cut Sparsifier

Cut vs Spectral Sparsifiers • Number of Constraints: – Cut: w(±H(U)) = (1§²) u(±G(U)) 8 UµV (2 n constraints) – Spectral: x. TLHx = (1§²) x. TLGx 8 x 2 RV (1 constraints) • Spectral constraints are SDP feasibility constraints: (1 -²) x. T LG x · x. T LH x · (1+²) x. T LG x 8 x 2 RV , (1 -²) LG ¹ LH ¹ (1+²) LG Here X ¹ Y means Y-X is positive semidefinite • Spectral constraints are actually easier to handle – Checking “Is H is a spectral sparsifier of G? ” is in P – Checking “Is H is a cut sparsifier of G? ” is non-uniform sparsest cut, so NP-hard

Application of Spectral Sparsifiers • Suppose you wanted to solve LG x = b • Since (1 -²) LG ¹ LH ¹ (1+²) LG we have (1 -²) LG-1 b · LH-1 b · (1+²) LG-1 b • Hope: Solving LH-1 b is easier since H is sparse • Theorem: [Spielman-Teng ‘ 04, Koutis-Miller-Peng ‘ 10] An approximate solution to LG x = b can be found in O(m log n (log n)2) time. (m = # edges of G)

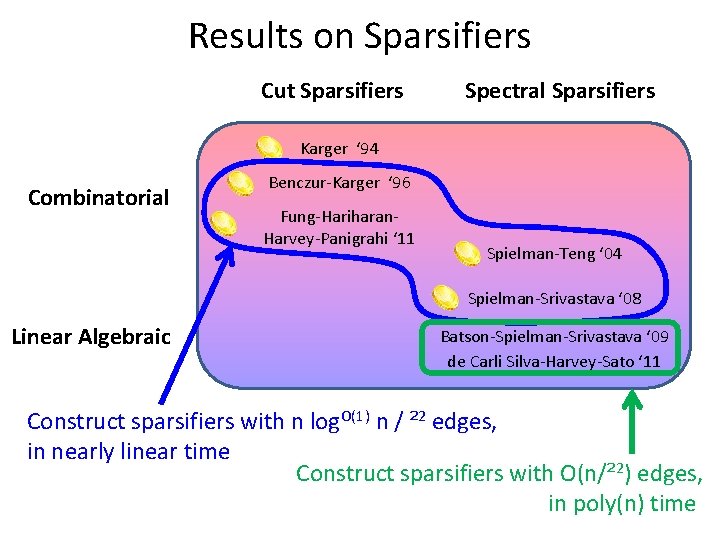
Results on Sparsifiers Cut Sparsifiers Spectral Sparsifiers Karger ‘ 94 Combinatorial Benczur-Karger ‘ 96 Fung-Hariharan. Harvey-Panigrahi ‘ 11 Spielman-Teng ‘ 04 Spielman-Srivastava ‘ 08 Linear Algebraic Batson-Spielman-Srivastava ‘ 09 de Carli Silva-Harvey-Sato ‘ 11 Construct sparsifiers with n log. O(1) n / ² 2 edges, in nearly linear time Construct sparsifiers with O(n/² 2) edges, in poly(n) time

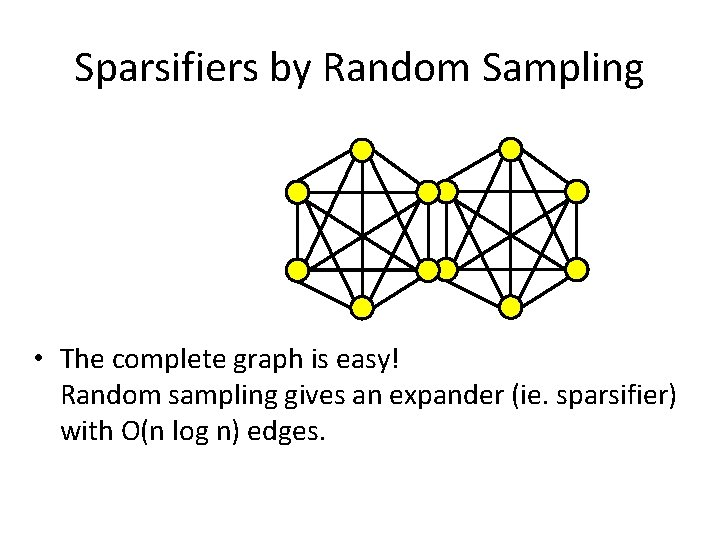
Sparsifiers by Random Sampling • The complete graph is easy! Random sampling gives an expander (ie. sparsifier) with O(n log n) edges.

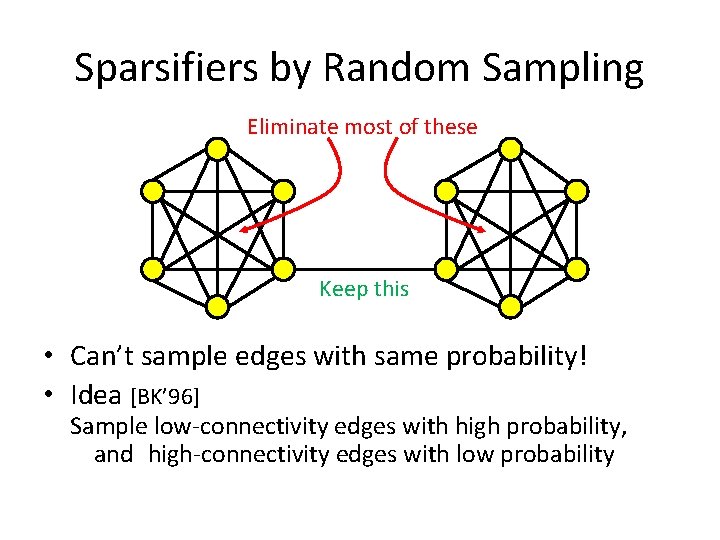
Sparsifiers by Random Sampling Eliminate most of these Keep this • Can’t sample edges with same probability! • Idea [BK’ 96] Sample low-connectivity edges with high probability, and high-connectivity edges with low probability

Non-uniform sampling algorithm [BK’ 96] • Input: Graph G=(V, E), weights u : E ! R+ • Output: A subgraph H=(V, F) with weights w : F ! R+ Choose parameter ½ Compute probabilities { pe : e 2 E } For i=1 to ½ For each edge e 2 E With probability pe, Add e to F Increase we by ue/(½pe) Can we do this so that the cut values are tightly concentrated and E[|F|]=nlog. O(1) n? • Note: E[|F|] · ½ ¢ e pe • Note: E[ we ] = ue 8 e 2 E ) For every UµV, E[ w(±H(U)) ] = u(±G(U))

Benczur-Karger ‘ 96 • Input: Graph G=(V, E), weights u : E ! R+ • Output: A subgraph H=(V, F) with weights w : F ! R+ Choose parameter ½ Compute probabilities { pe : e 2 E } For i=1 to ½ For. But each edge e 2 E what is “strength”? With p e, Can’t weprobability use “connectivity”? Add e to F Increase we by ue/(½pe) Can we do this so that the cut values are tightly concentrated and E[|F|]=nlog. O(1) n? Can approximate all values in m log. O(1) n time.

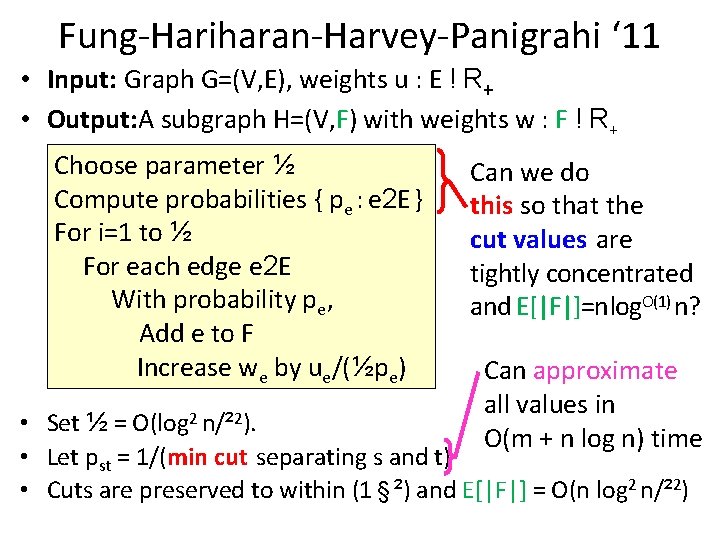
Fung-Hariharan-Harvey-Panigrahi ‘ 11 • Input: Graph G=(V, E), weights u : E ! R+ • Output: A subgraph H=(V, F) with weights w : F ! R+ Choose parameter ½ Compute probabilities { pe : e 2 E } For i=1 to ½ For each edge e 2 E With probability pe, Add e to F Increase we by ue/(½pe) Can we do this so that the cut values are tightly concentrated and E[|F|]=nlog. O(1) n? Can approximate all values in O(m + n log n) time • Set ½ = O(log 2 n/² 2). • Let pst = 1/(min cut separating s and t) • Cuts are preserved to within (1 § ²) and E[|F|] = O(n log 2 n/² 2)

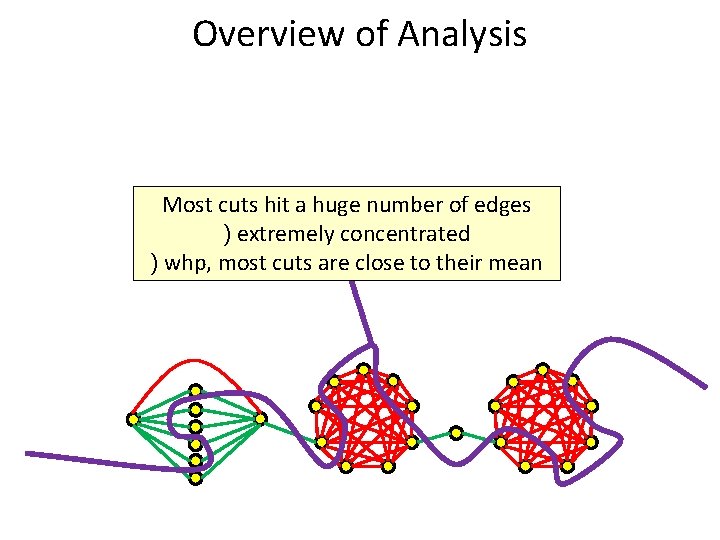
Overview of Analysis Most cuts hit a huge number of edges ) extremely concentrated ) whp, most cuts are close to their mean

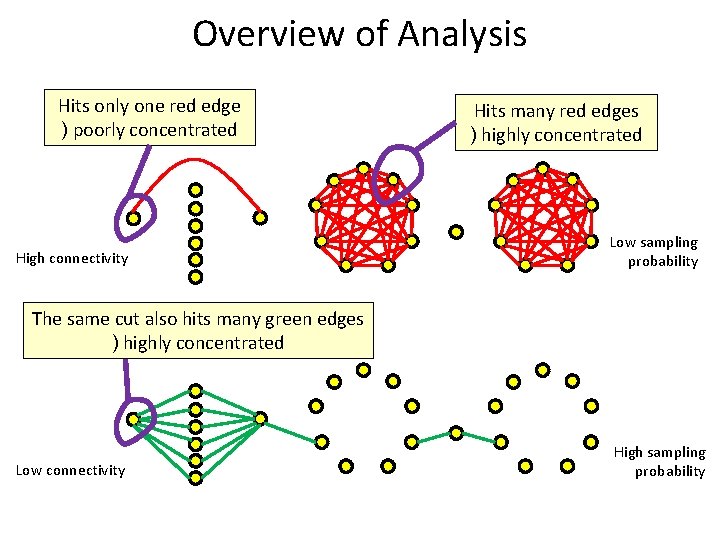
Overview of Analysis Hits only one red edge ) poorly concentrated High connectivity Hits many red edges ) highly concentrated Low sampling probability The same cut also hits many green edges ) highly concentrated Low connectivity High sampling probability

Summary for Cut Sparsifiers • Do non-uniform sampling of edges, with probabilities based on “connectivity” • Decomposes graph into “connectivity classes” and argue concentration of all cuts • BK’ 96 used “strength” not “connectivity” • Can get sparsifiers with O(n log n / ² 2) edges – Optimal for any independent sampling algorithm

Spectral Sparsification • Input: Graph G=(V, E), weights u : E ! R+ • Recall: x. T LG x = st 2 E ust (xs-xt)2 Call this x. T Lst x • Goal: Find weights w : E ! R+ such that most we are zero, and (1 -²) x. T LG x · , (1 - ²) LG ¹ e 2 E we x. T Le x · (1+²) x. T LG x 8 x 2 RV e 2 E we Le ¹ (1+²) LG • General Problem: Given matrices Le satisfying e Le = LG, find coefficients we, mostly zero, such that (1 -²) LG ¹ e we Le ¹ (1+²) LG

The General Problem: Sparsifying Sums of PSD Matrices • General Problem: Given PSD matrices Le s. t. e Le = L, find coefficients we, mostly zero, such that (1 -²) L ¹ e we Le ¹ (1+²) L • Theorem: [Ahlswede-Winter ’ 02] Random sampling gives w with O( n log n/² 2 ) non-zeros. • Theorem: [de Carli Silva-Harvey-Sato ‘ 11], building on [Batson-Spielman-Srivastava ‘ 09] Deterministic alg gives w with O( n/² 2 ) non-zeros. – Cut & spectral sparsifiers with O(n/² 2) edges [BSS’ 09] – Sparsifiers with more properties and O(n/² 2) edges [d. HS’ 11]

Vector Case • General Vector problem: vectors ve 2[0, 1]n. Les. t. Problem: Given PSD matrices s. t. ee v. Lee == v, L, find coefficients we, mostly zero, such that wee w vee L- ev¹ k(1+²) (1 -²)k L ¹e 1 · ² L • Theorem [Althofer ‘ 94, Lipton-Young ‘ 94]: There is a w with O(log n/² 2) non-zeros. • Proof: Random sampling & Hoeffding inequality. • Multiplicative version: There is a w with O(n log n/² 2) non-zeros such that (1 -²) v · e we ve · (1+²) v

Concentration Inequalities The only difference

“Balls & Bins” Example

Solving the General Problem

Derandomization

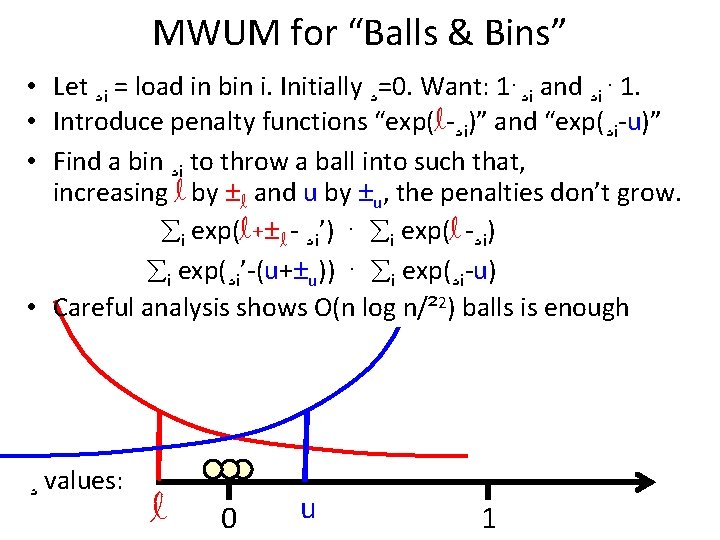
MWUM for “Balls & Bins” • Let ¸i = load in bin i. Initially ¸=0. Want: 1·¸i and ¸i · 1. • Introduce penalty functions “exp(l-¸i)” and “exp(¸i-u)” • Find a bin ¸i to throw a ball into such that, increasing l by ±l and u by ±u, the penalties don’t grow. i exp(l+±l - ¸i’) · i exp(l -¸i) i exp(¸i’-(u+±u)) · i exp(¸i-u) • Careful analysis shows O(n log n/² 2) balls is enough ¸ values: l 0 u 1

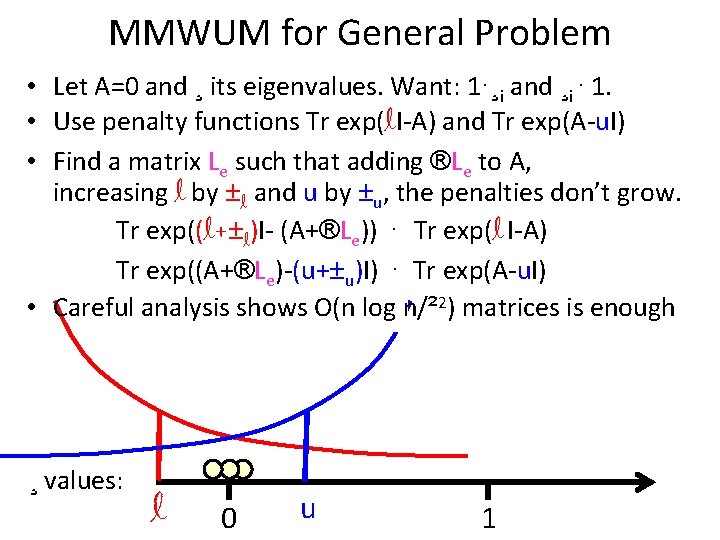
MMWUM for General Problem • Let A=0 and ¸ its eigenvalues. Want: 1·¸i and ¸i · 1. • Use penalty functions Tr exp(l. I-A) and Tr exp(A-u. I) • Find a matrix Le such that adding ®Le to A, increasing l by ±l and u by ±u, the penalties don’t grow. Tr exp((l+±l)I- (A+®Le)) · Tr exp(l I-A) Tr exp((A+®Le)-(u+±u)I) · Tr exp(A-u. I) • Careful analysis shows O(n log n/² 2) matrices is enough ¸ values: l 0 u 1

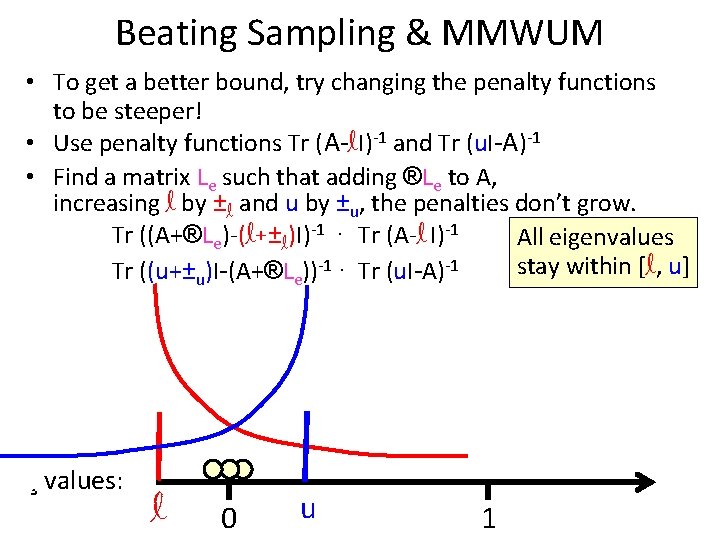
Beating Sampling & MMWUM • To get a better bound, try changing the penalty functions to be steeper! • Use penalty functions Tr (A-l. I)-1 and Tr (u. I-A)-1 • Find a matrix Le such that adding ®Le to A, increasing l by ±l and u by ±u, the penalties don’t grow. Tr ((A+®Le)-(l+±l)I)-1 · Tr (A-l I)-1 All eigenvalues stay within [l, u] Tr ((u+±u)I-(A+®Le))-1 · Tr (u. I-A)-1 ¸ values: l 0 u 1

Beating Sampling & MMWUM

Applications

Open Questions • Sparsifiers for directed graphs • More constructions of sparsifiers with O(n/² 2) edges. Perhaps randomized? • Iterative construction of expander graphs • More control of the weights we • A combinatorial proof of spectral sparsifiers • More applications of our general theorem