Graph Searching Algorithms S Tree BreadthFirst Search BFS

Graph Searching Algorithms S
Tree
Breadth-First Search (BFS)
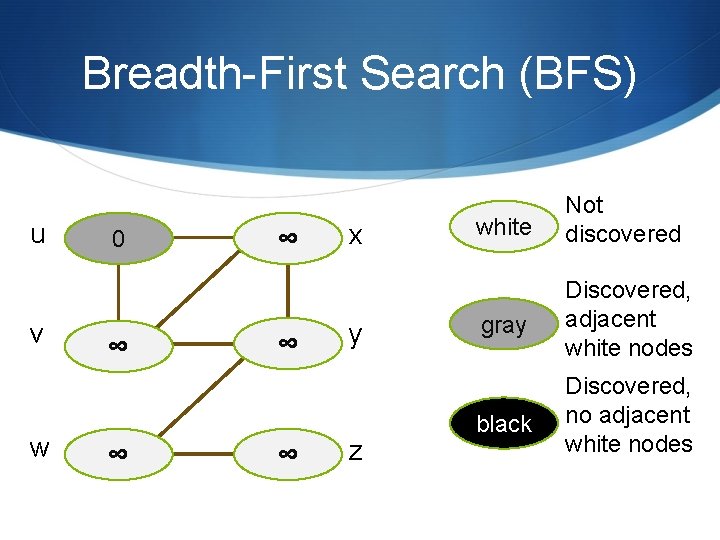
Breadth-First Search (BFS) u v w 0 ∞ ∞ ∞ x y z white Not discovered gray Discovered, adjacent white nodes black Discovered, no adjacent white nodes
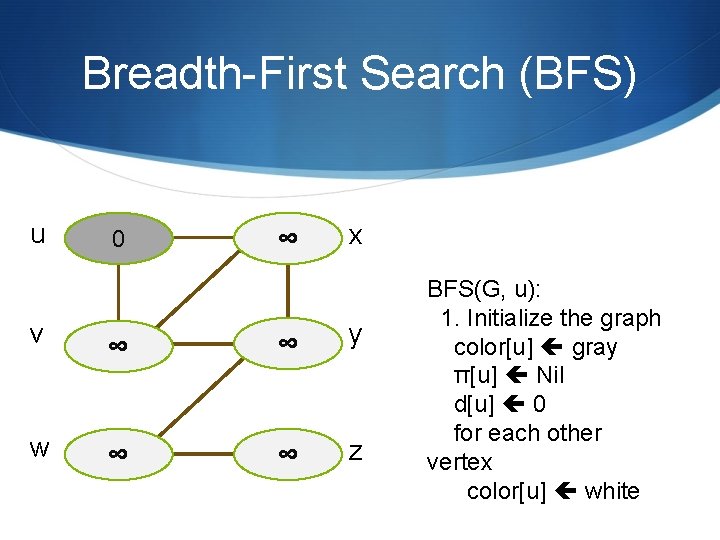
Breadth-First Search (BFS) u v w 0 ∞ x ∞ ∞ y ∞ ∞ z BFS(G, u): 1. Initialize the graph color[u] gray π[u] Nil d[u] 0 for each other vertex color[u] white
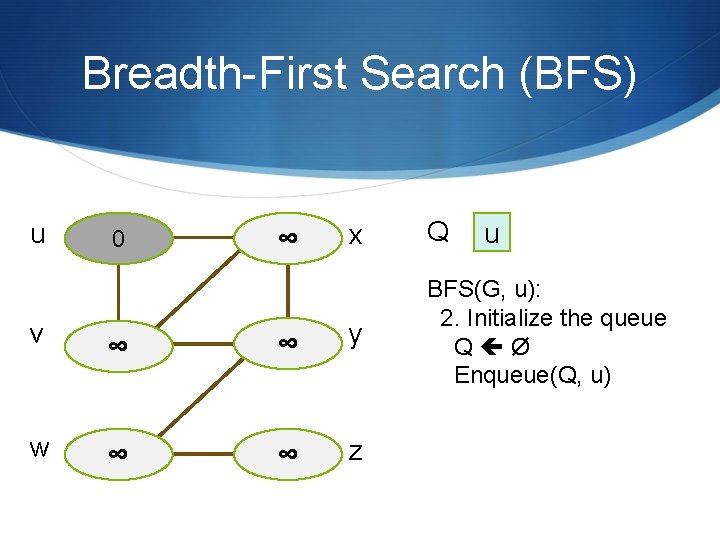
Breadth-First Search (BFS) u 0 ∞ v ∞ ∞ w ∞ ∞ x Q y BFS(G, u): 2. Initialize the queue Q Ø Enqueue(Q, u) z u

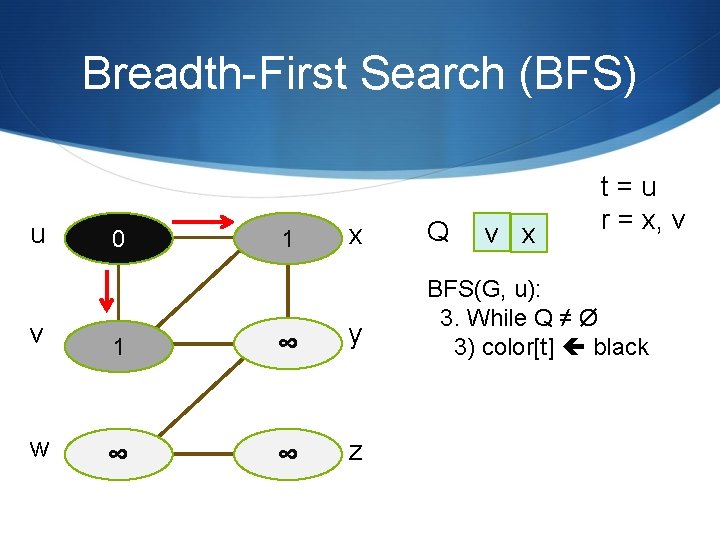
Breadth-First Search (BFS) t=u u 0 ∞ v ∞ ∞ w ∞ ∞ x Q y BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) z

Breadth-First Search (BFS) u 0 1 x v 1 ∞ y w ∞ ∞ z Q v x t=u r = x, v BFS(G, u): 3. While Q ≠ Ø 2) for each r adj to t if color[r] = white color[r] gray π[r] t d[r] d[t] + 1 Enqueue(Q, r)
Breadth-First Search (BFS) u 0 1 t=u r = x, v x Q BFS(G, u): 3. While Q ≠ Ø 3) color[t] black v 1 ∞ y w ∞ ∞ z v x
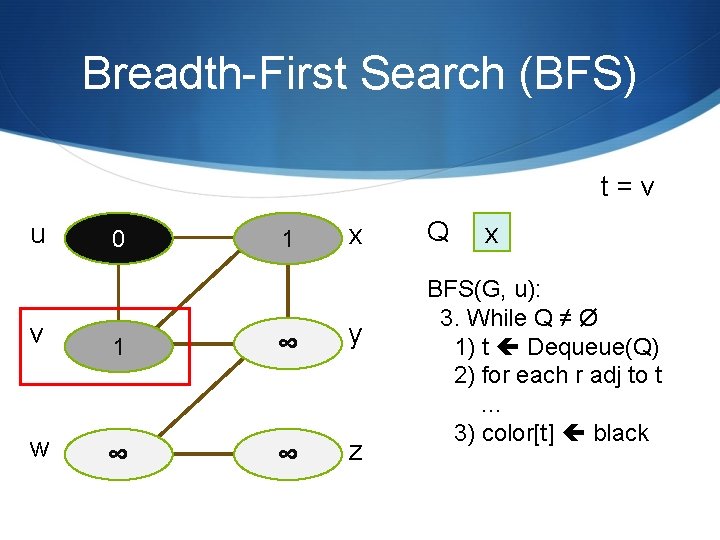
Breadth-First Search (BFS) t=v u 0 1 x v 1 ∞ y w ∞ ∞ z Q x BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) 2) for each r adj to t … 3) color[t] black
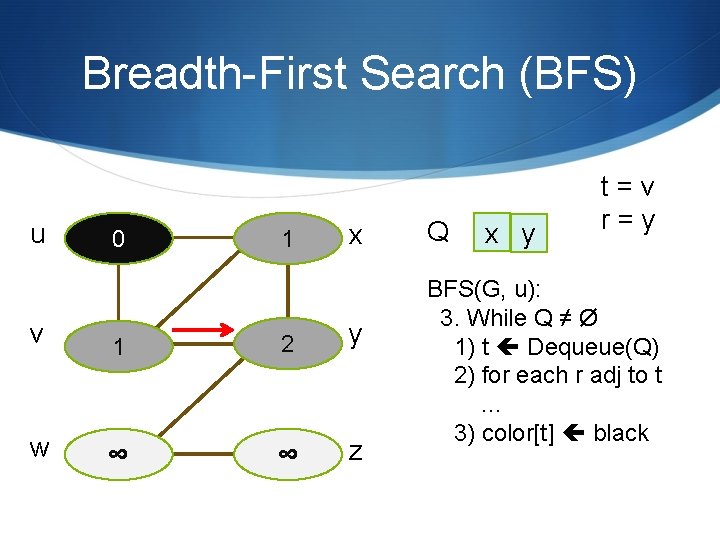
Breadth-First Search (BFS) u 0 1 x v 1 2 y w ∞ ∞ z Q x y t=v r=y BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) 2) for each r adj to t … 3) color[t] black
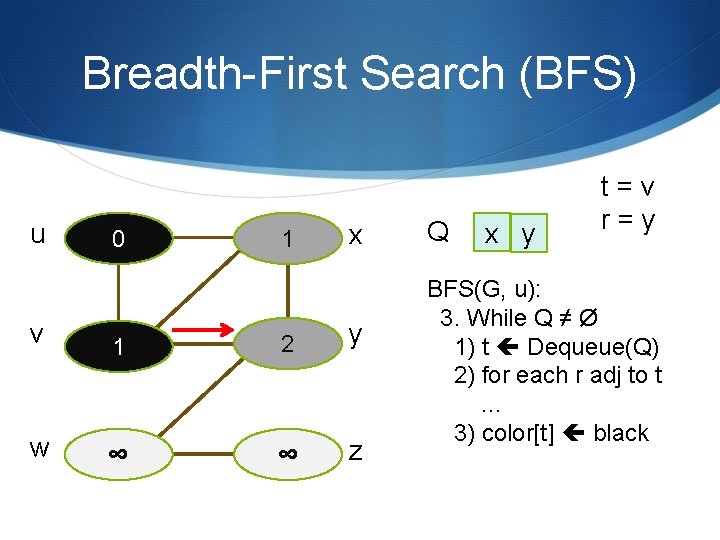
Breadth-First Search (BFS) u 0 1 x v 1 2 y w ∞ ∞ z Q x y t=v r=y BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) 2) for each r adj to t … 3) color[t] black
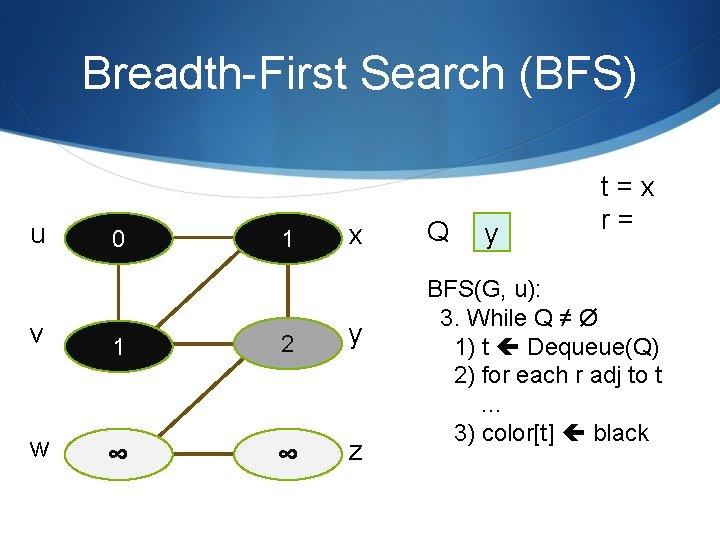
Breadth-First Search (BFS) u 0 1 x v 1 2 y w ∞ ∞ z Q y t=x r= BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) 2) for each r adj to t … 3) color[t] black
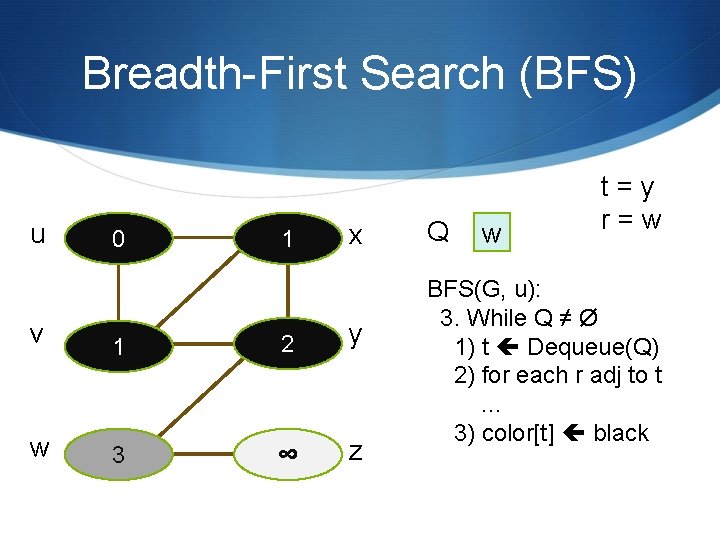
Breadth-First Search (BFS) u 0 1 x v 1 2 y w 3 ∞ z Q w t=y r=w BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) 2) for each r adj to t … 3) color[t] black
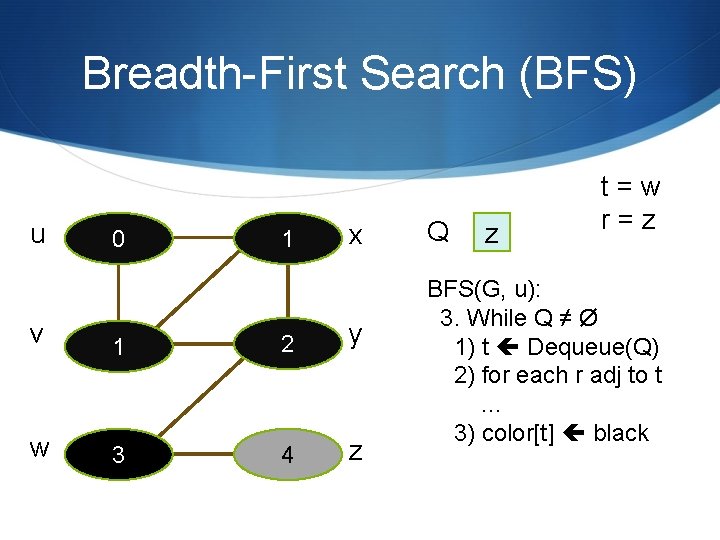
Breadth-First Search (BFS) u 0 1 x v 1 2 y w 3 4 z Q z t=w r=z BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) 2) for each r adj to t … 3) color[t] black

Breadth-First Search (BFS) u 0 1 x v 1 2 y w 3 4 z Q t=z r= BFS(G, u): 3. While Q ≠ Ø 1) t Dequeue(Q) 2) for each r adj to t … 3) color[t] black
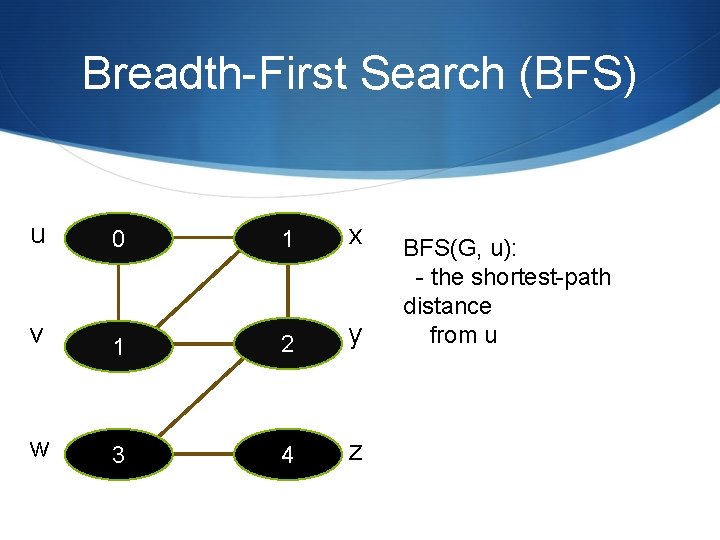
Breadth-First Search (BFS) u 0 1 x v 1 2 y w 3 4 z BFS(G, u): - the shortest-path distance from u
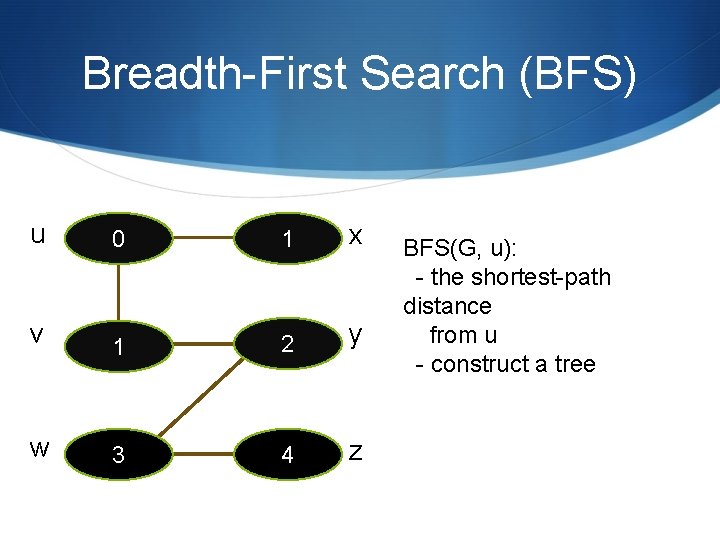
Breadth-First Search (BFS) u 0 1 x v 1 2 y w 3 4 z BFS(G, u): - the shortest-path distance from u - construct a tree
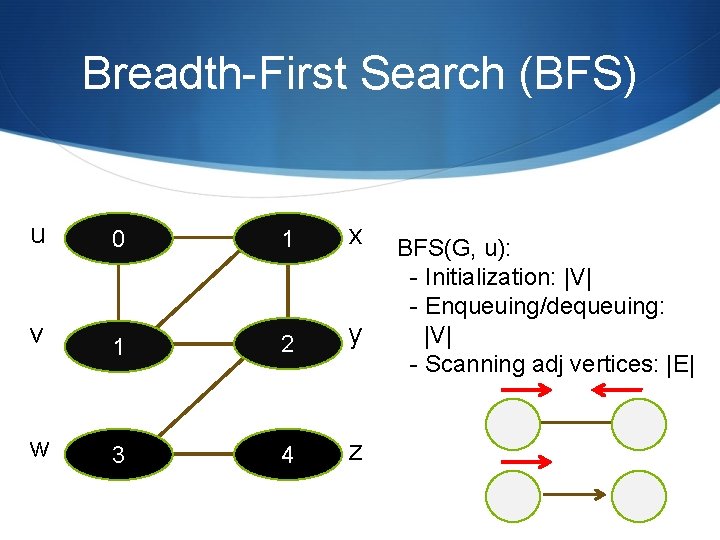
Breadth-First Search (BFS) u 0 1 x v 1 2 y w 3 4 z BFS(G, u): - Initialization: |V| - Enqueuing/dequeuing: |V| - Scanning adj vertices: |E|
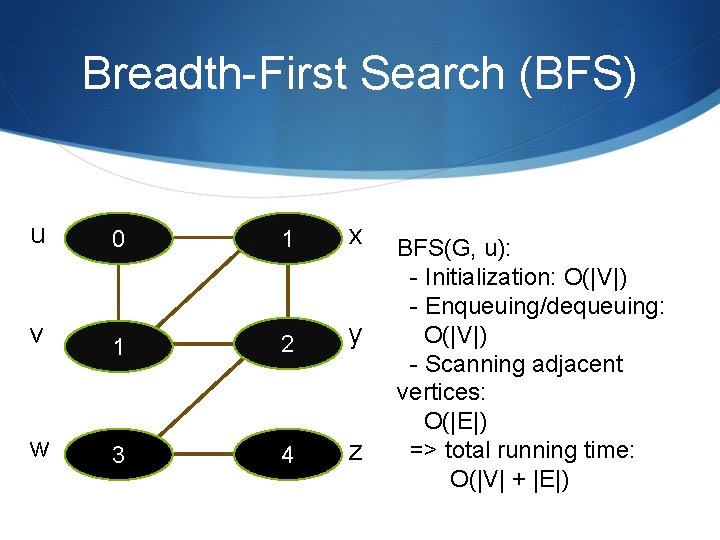
Breadth-First Search (BFS) u 0 1 x v 1 2 y w 3 4 z BFS(G, u): - Initialization: O(|V|) - Enqueuing/dequeuing: O(|V|) - Scanning adjacent vertices: O(|E|) => total running time: O(|V| + |E|)
Depth-First Search (DFS)
![Depth-First Search (DFS) d[u]: when u is discovered f[u]: when searching adj of u Depth-First Search (DFS) d[u]: when u is discovered f[u]: when searching adj of u](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-22.jpg)
Depth-First Search (DFS) d[u]: when u is discovered f[u]: when searching adj of u is finished u v w
![Depth-First Search (DFS) timestamp: t d[u] = t d[u]: when u is discovered f[u]: Depth-First Search (DFS) timestamp: t d[u] = t d[u]: when u is discovered f[u]:](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-23.jpg)
Depth-First Search (DFS) timestamp: t d[u] = t d[u]: when u is discovered f[u]: when searching adj of u is finished u v w
![Depth-First Search (DFS) timestamp: t+1 d[u] = t d[u]: when u is discovered f[u]: Depth-First Search (DFS) timestamp: t+1 d[u] = t d[u]: when u is discovered f[u]:](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-24.jpg)
Depth-First Search (DFS) timestamp: t+1 d[u] = t d[u]: when u is discovered f[u]: when searching adj of u is finished u v d[v] = t+1 w
![Depth-First Search (DFS) timestamp: t+2 d[u] = t d[u]: when u is discovered f[u]: Depth-First Search (DFS) timestamp: t+2 d[u] = t d[u]: when u is discovered f[u]:](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-25.jpg)
Depth-First Search (DFS) timestamp: t+2 d[u] = t d[u]: when u is discovered f[u]: when searching adj of u is finished u v d[v] = t+1 f[v] = t+2 w
![Depth-First Search (DFS) timestamp: t+3 d[u] = t d[u]: when u is discovered f[u]: Depth-First Search (DFS) timestamp: t+3 d[u] = t d[u]: when u is discovered f[u]:](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-26.jpg)
Depth-First Search (DFS) timestamp: t+3 d[u] = t d[u]: when u is discovered f[u]: when searching adj of u is finished u v d[v] = t+1 f[v] = t+2 w d[w] = t+3
![Depth-First Search (DFS) timestamp: t+4 d[u] = t d[u]: when u is discovered f[u]: Depth-First Search (DFS) timestamp: t+4 d[u] = t d[u]: when u is discovered f[u]:](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-27.jpg)
Depth-First Search (DFS) timestamp: t+4 d[u] = t d[u]: when u is discovered f[u]: when searching adj of u is finished u v d[v] = t+1 f[v] = t+2 w d[w] = t+3 f[v] = t+4
![Depth-First Search (DFS) timestamp: t+5 d[u] = t f[u] = t+5 d[u]: when u Depth-First Search (DFS) timestamp: t+5 d[u] = t f[u] = t+5 d[u]: when u](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-28.jpg)
Depth-First Search (DFS) timestamp: t+5 d[u] = t f[u] = t+5 d[u]: when u is discovered f[u]: when searching adj of u is finished u v d[v] = t+1 f[v] = t+2 w d[w] = t+3 f[w] = t+4
![Depth-First Search (DFS) d[u] = t f[u] = t+5 d[u]: when u is discovered Depth-First Search (DFS) d[u] = t f[u] = t+5 d[u]: when u is discovered](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-29.jpg)
Depth-First Search (DFS) d[u] = t f[u] = t+5 d[u]: when u is discovered f[u]: when searching adj of u is finished u v d[v] = t+1 f[v] = t+2 w d[w] = t+3 f[w] = t+4 1. d[u] < f[u] 2. [ d[u], f[u] ] entirely contains [ d[v], f[v] ] 3. [ d[v], f[v] ] and [ d[w], f[w] ] are entirely disjoint
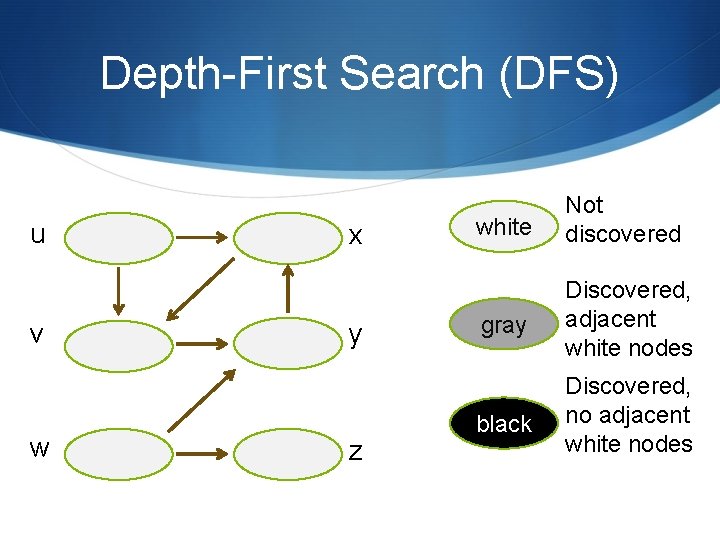
Depth-First Search (DFS) u v w x y z white Not discovered gray Discovered, adjacent white nodes black Discovered, no adjacent white nodes
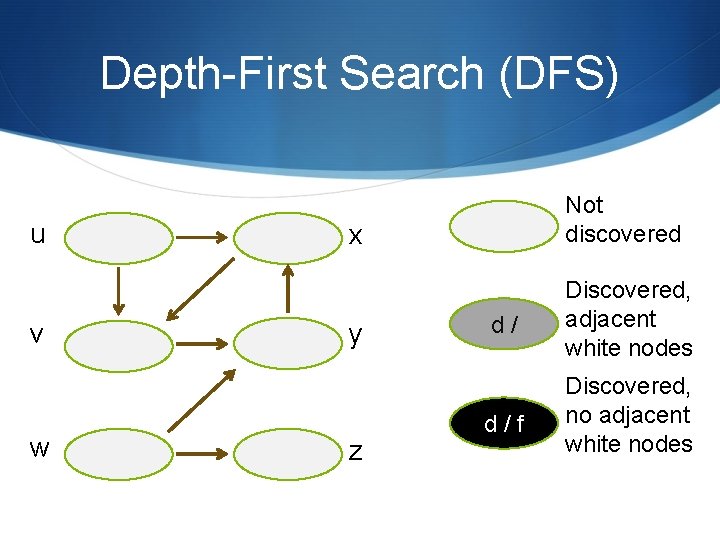
Depth-First Search (DFS) u v w Not discovered x y z d/ Discovered, adjacent white nodes d/f Discovered, no adjacent white nodes
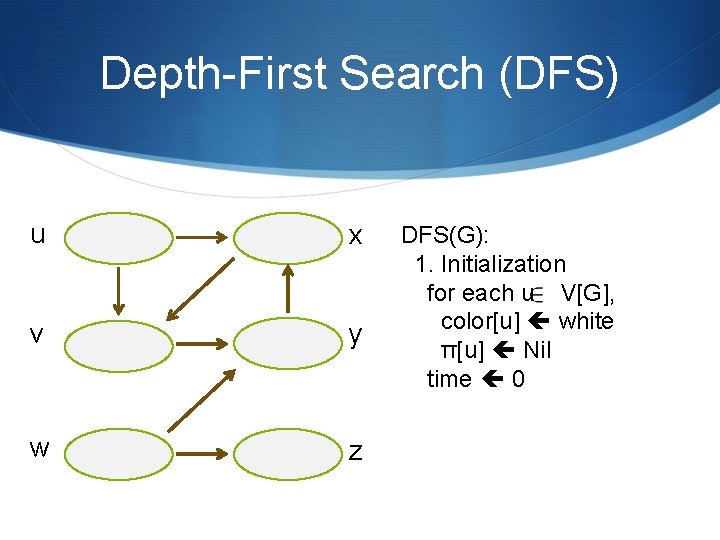
Depth-First Search (DFS) u x v y w z DFS(G): 1. Initialization for each u V[G], color[u] white π[u] Nil time 0
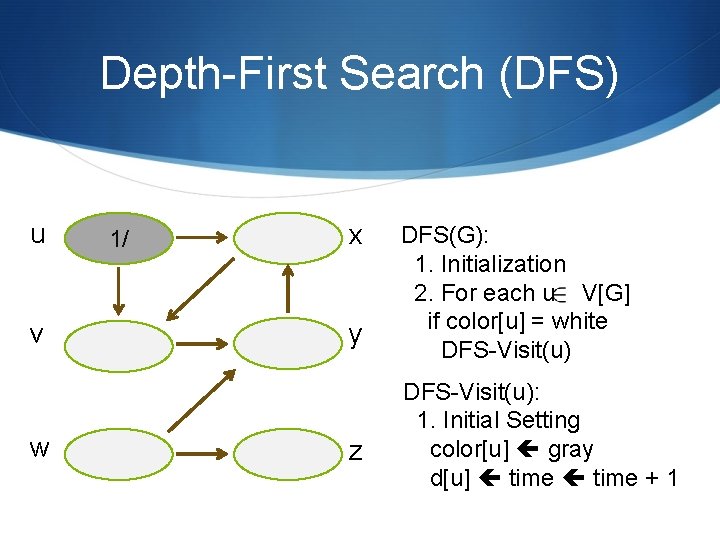
Depth-First Search (DFS) u v w 1/ x y z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting color[u] gray d[u] time + 1
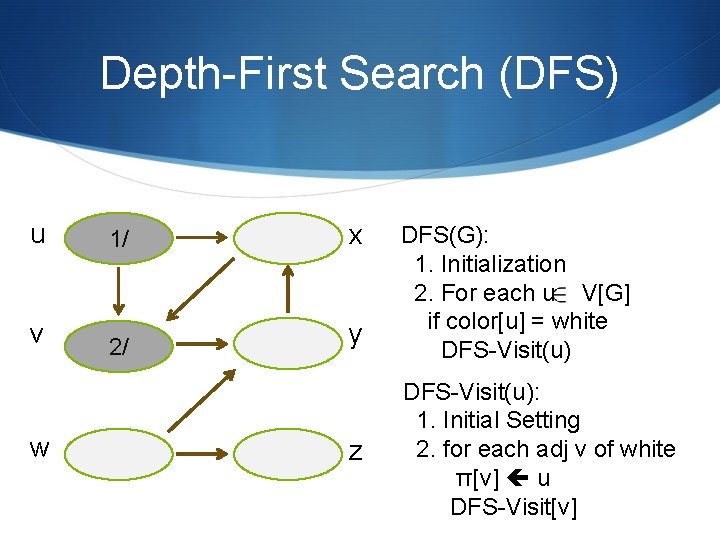
Depth-First Search (DFS) u 1/ x v 2/ y w z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. for each adj v of white π[v] u DFS-Visit[v]
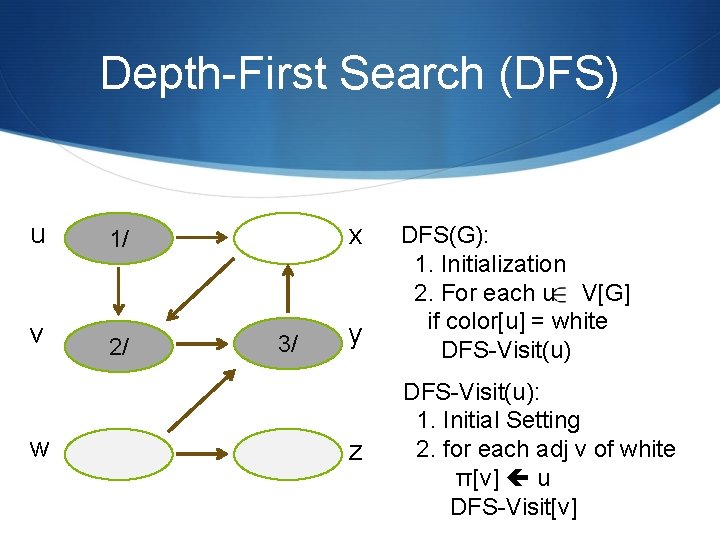
Depth-First Search (DFS) u 1/ v 2/ w x 3/ y z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. for each adj v of white π[v] u DFS-Visit[v]
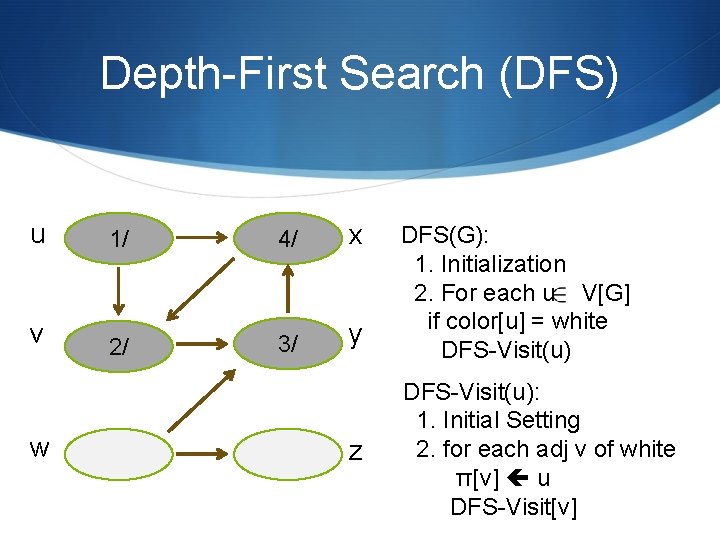
Depth-First Search (DFS) u 1/ 4/ x v 2/ 3/ y w z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. for each adj v of white π[v] u DFS-Visit[v]
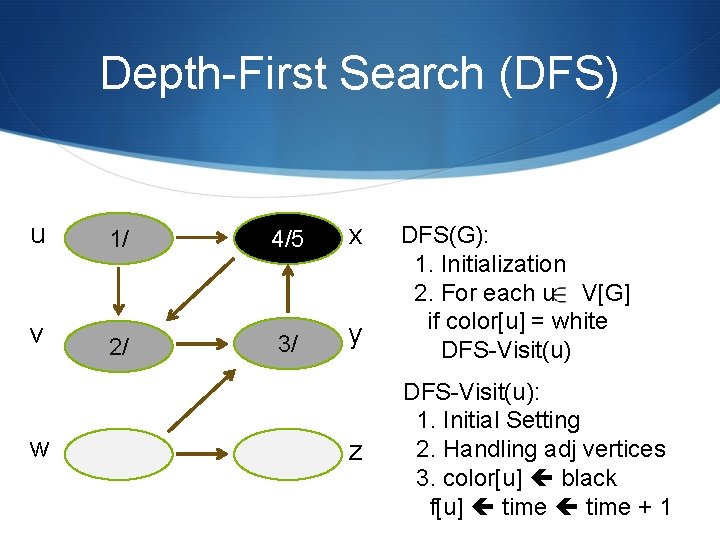
Depth-First Search (DFS) u 1/ 4/5 x v 2/ 3/ y w z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1
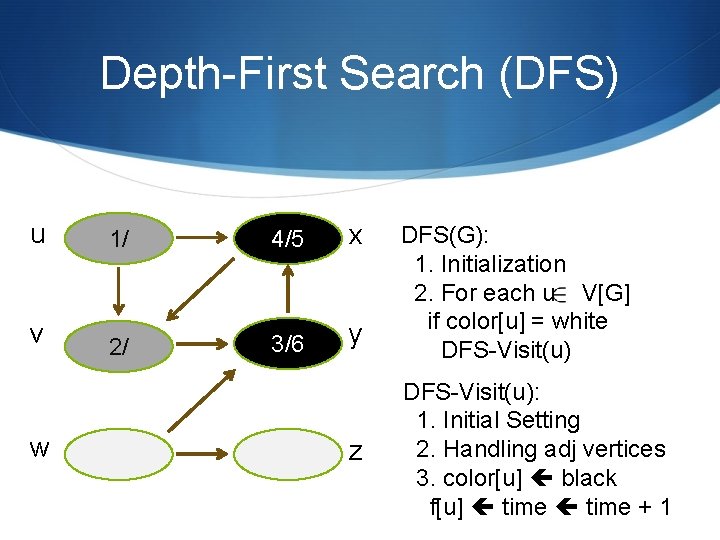
Depth-First Search (DFS) u 1/ 4/5 x v 2/ 3/6 y w z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1
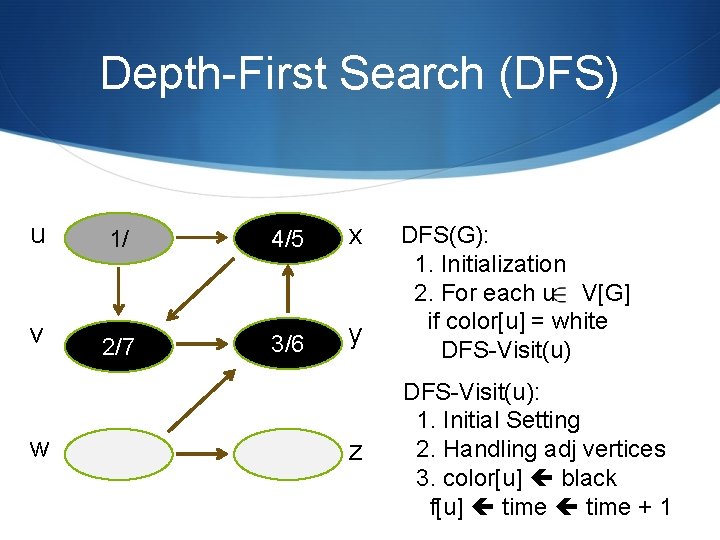
Depth-First Search (DFS) u 1/ 4/5 x v 2/7 3/6 y w z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1
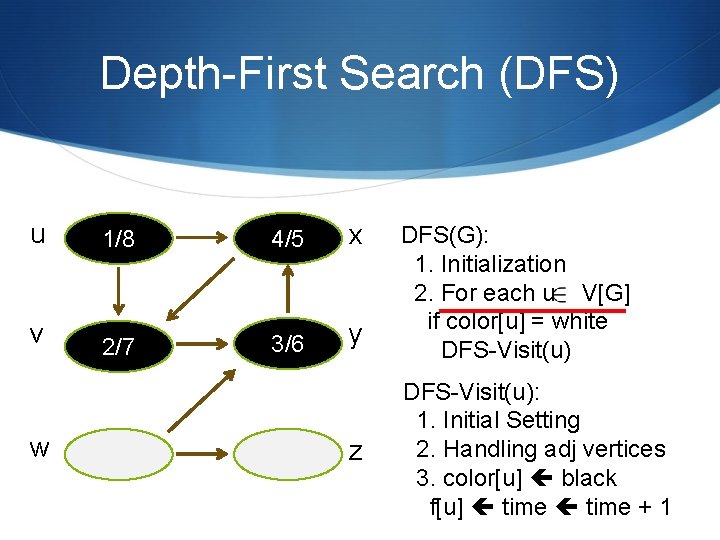
Depth-First Search (DFS) u 1/8 4/5 x v 2/7 3/6 y w z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1

Depth-First Search (DFS) u 1/8 4/5 x v 2/7 3/6 y w 9/ z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1

Depth-First Search (DFS) u 1/8 4/5 x v 2/7 3/6 y w 9/ 10/ z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1
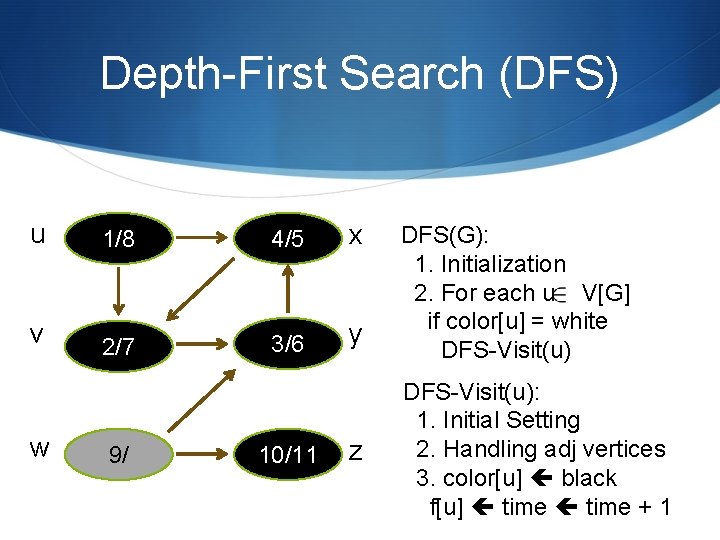
Depth-First Search (DFS) u 1/8 4/5 x v 2/7 3/6 y w 9/ 10/11 z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1
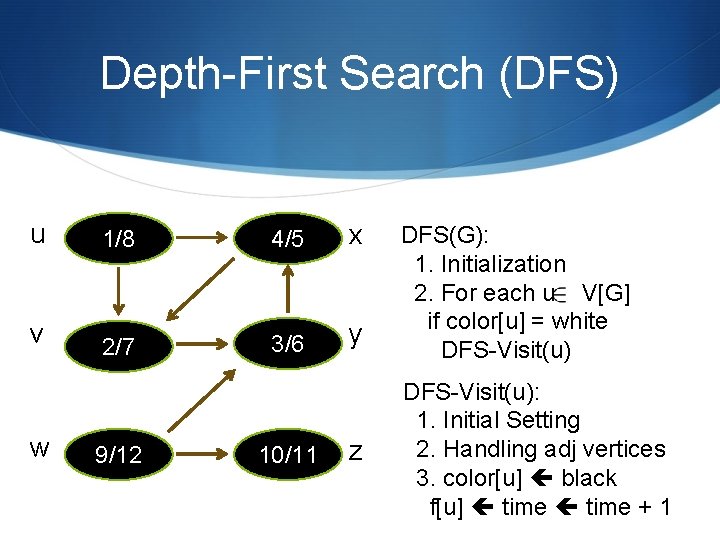
Depth-First Search (DFS) u 1/8 4/5 x v 2/7 3/6 y w 9/12 10/11 z DFS(G): 1. Initialization 2. For each u V[G] if color[u] = white DFS-Visit(u): 1. Initial Setting 2. Handling adj vertices 3. color[u] black f[u] time + 1
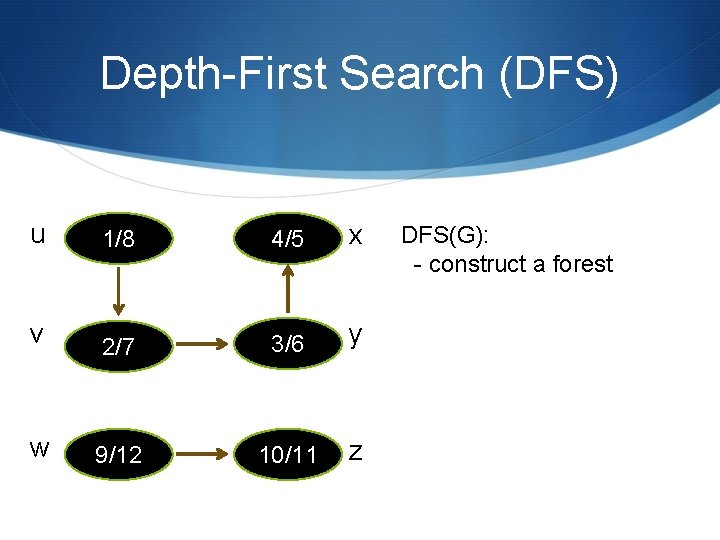
Depth-First Search (DFS) u 1/8 4/5 x v 2/7 3/6 y w 9/12 10/11 z DFS(G): - construct a forest
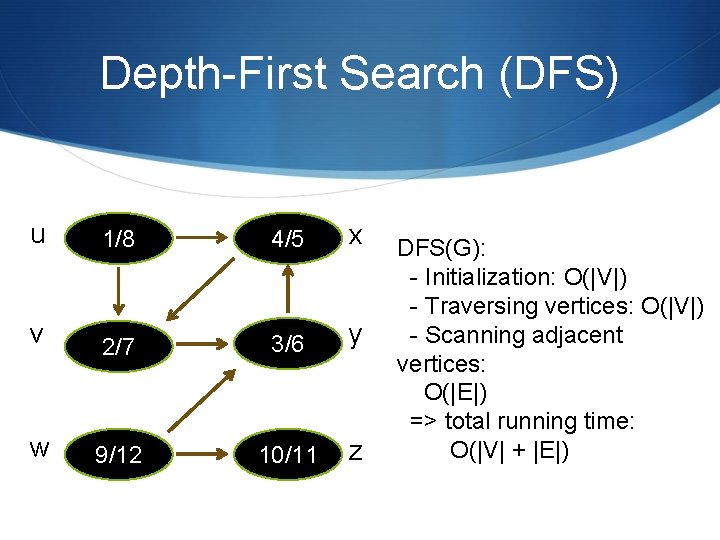
Depth-First Search (DFS) u 1/8 4/5 x v 2/7 3/6 y w 9/12 10/11 z DFS(G): - Initialization: O(|V|) - Traversing vertices: O(|V|) - Scanning adjacent vertices: O(|E|) => total running time: O(|V| + |E|)
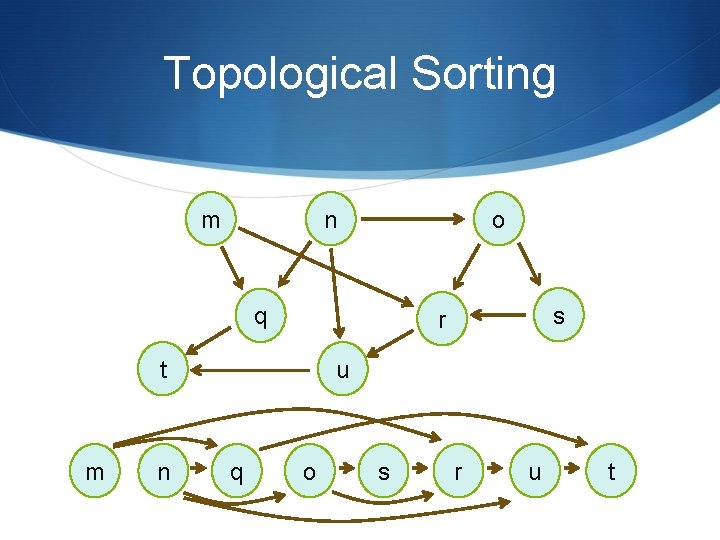
Topological Sorting m n o q t m n s r u q o s r u t
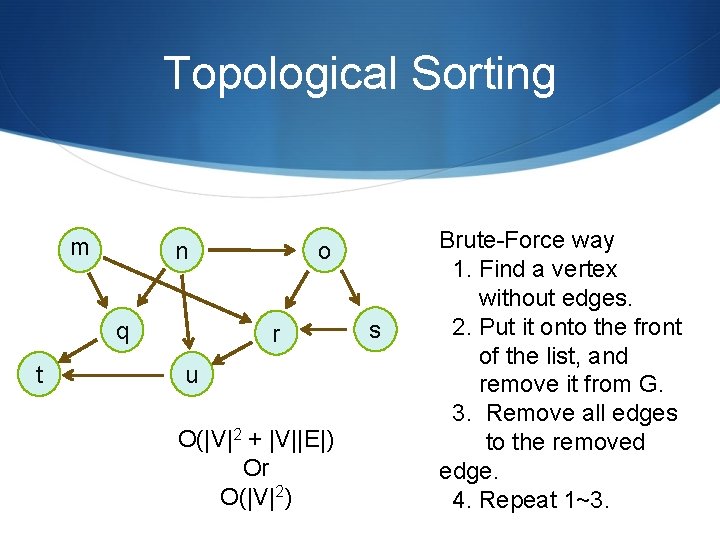
Topological Sorting m n q t o r u O(|V|2 + |V||E|) Or O(|V|2) s Brute-Force way 1. Find a vertex without edges. 2. Put it onto the front of the list, and remove it from G. 3. Remove all edges to the removed edge. 4. Repeat 1~3.
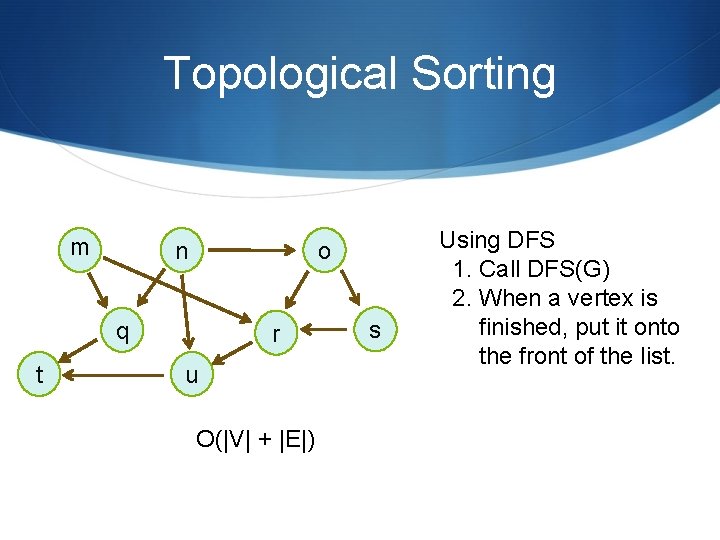
Topological Sorting m n o q t r u O(|V| + |E|) s Using DFS 1. Call DFS(G) 2. When a vertex is finished, put it onto the front of the list.
![Topological Sorting v enters the list before u? v At d[u]: u Using DFS Topological Sorting v enters the list before u? v At d[u]: u Using DFS](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-50.jpg)
Topological Sorting v enters the list before u? v At d[u]: u Using DFS 1. Call DFS(G) 2. When a vertex is finished, put it onto the front of the list. 1) v is white: d[u] < d[v] < f[u] 2) v is black: f[v] < d[u] 3) v is gray: d[v] < d[u] < f[v]
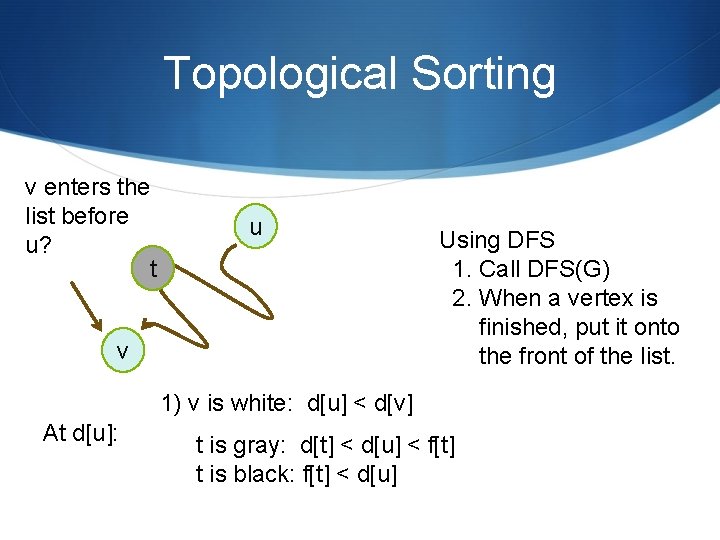
Topological Sorting v enters the list before u? t u v Using DFS 1. Call DFS(G) 2. When a vertex is finished, put it onto the front of the list. 1) v is white: d[u] < d[v] At d[u]: t is gray: d[t] < d[u] < f[t] t is black: f[t] < d[u]
![Topological Sorting u v w 1. If v is a descendant, d[u] < d[v] Topological Sorting u v w 1. If v is a descendant, d[u] < d[v]](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-52.jpg)
Topological Sorting u v w 1. If v is a descendant, d[u] < d[v] < f[u] 2. If v is an anscestor, d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v]
![Depth-First Search (DFS) 1. d[u] < f[u] 2. [ d[u], f[u] ] entirely contains Depth-First Search (DFS) 1. d[u] < f[u] 2. [ d[u], f[u] ] entirely contains](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-53.jpg)
Depth-First Search (DFS) 1. d[u] < f[u] 2. [ d[u], f[u] ] entirely contains [ d[v], f[v] ] 3. [ d[v], f[v] ] and [ d[w], f[w] ] are entirely disjoint u v w In a depth-first forest, v is a descendant of u if and only if d[u] < d[v] < f[u]
![Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u] Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u]](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-54.jpg)
Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u] G is not acyclic. 2. If v is an anscestor, d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v] u t At d[u]: 1) v is white: d[u] < d[v] t is gray: d[t] < d[u] < f[t] t is black: f[t] < d[u] v
![Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u] Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u]](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-55.jpg)
Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u] v should be 2. If v is an anscestor, black. d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v] u t At d[u]: 1) v is white: d[u] < d[v] t is gray: d[t] < d[u] < f[t] t is black: f[t] < d[u] v
![Topological Sorting 1. If v is a descendant, d[u] < d[v] < f[u] 2. Topological Sorting 1. If v is a descendant, d[u] < d[v] < f[u] 2.](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-56.jpg)
Topological Sorting 1. If v is a descendant, d[u] < d[v] < f[u] 2. If v is an anscestor, d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v] u t At d[u]: 1) v is white: d[u] < d[v] t is white. v
![Topological Sorting 1. If v is a descendant, d[u] < d[v] < f[u] 2. Topological Sorting 1. If v is a descendant, d[u] < d[v] < f[u] 2.](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-57.jpg)
Topological Sorting 1. If v is a descendant, d[u] < d[v] < f[u] 2. If v is an anscestor, d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v] u t At d[u]: 1) v is white: d[u] < d[v] < f[u] t is white. v
![Topological Sorting 1. If v is a descendant, v will enter the d[u] < Topological Sorting 1. If v is a descendant, v will enter the d[u] <](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-58.jpg)
Topological Sorting 1. If v is a descendant, v will enter the d[u] < d[v] < f[u] list before u. 2. If v is an anscestor, d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v] u v At d[u]: 1) v is white: d[u] < d[v] < f[u] 2) v is black: f[v] < d[u] 3) v is gray: d[v] < d[u] < f[v]
![Topological Sorting 1. If v is a descendant, v is already in d[u] < Topological Sorting 1. If v is a descendant, v is already in d[u] <](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-59.jpg)
Topological Sorting 1. If v is a descendant, v is already in d[u] < d[v] < f[u] the list. 2. If v is an anscestor, d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v] u v At d[u]: 1) v is white: d[u] < d[v] < f[u] 2) v is black: f[v] < d[u] 3) v is gray: d[v] < d[u] < f[v]
![Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u] Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u]](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-60.jpg)
Topological Sorting 1. If v is a descendant, Contradiction: d[u] < d[v] < f[u] G is not acyclic. 2. If v is an anscestor, d[v] < d[u] < f[v] 3. Otherwise, d[v] < f[v] < d[u] < f[u] or d[u] < f[u] < d[v] < f[v] u v At d[u]: 1) v is white: d[u] < d[v] < f[u] 2) v is black: f[v] < d[u] 3) v is gray: d[v] < d[u] < f[v]
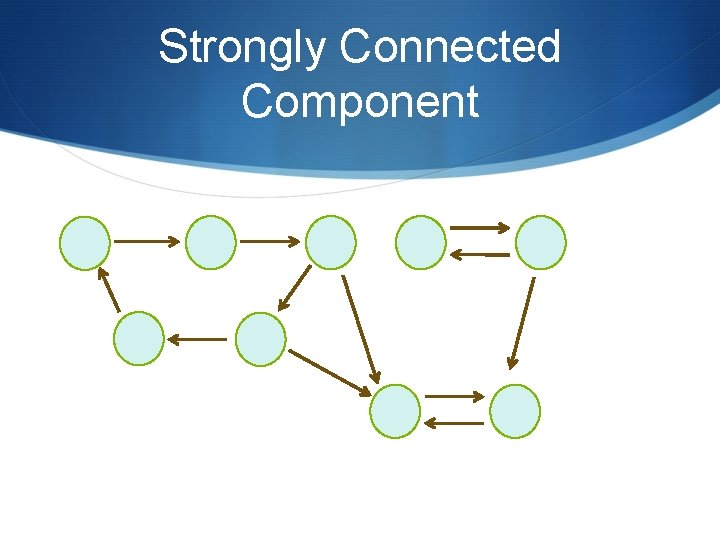
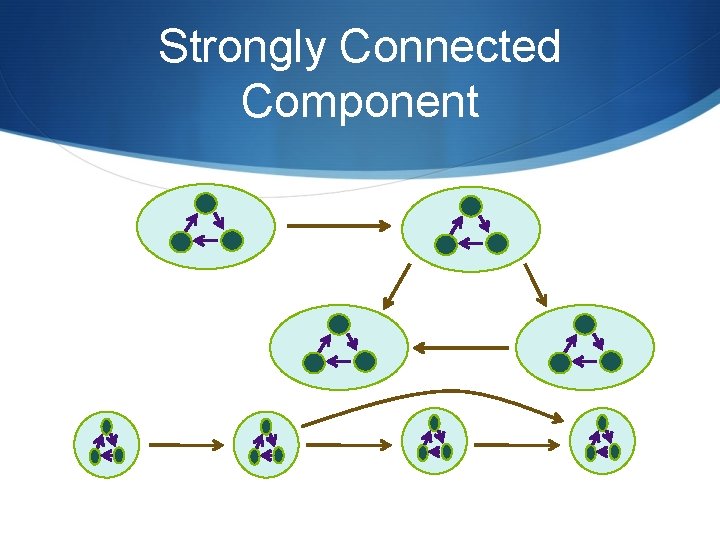
Strongly Connected Component
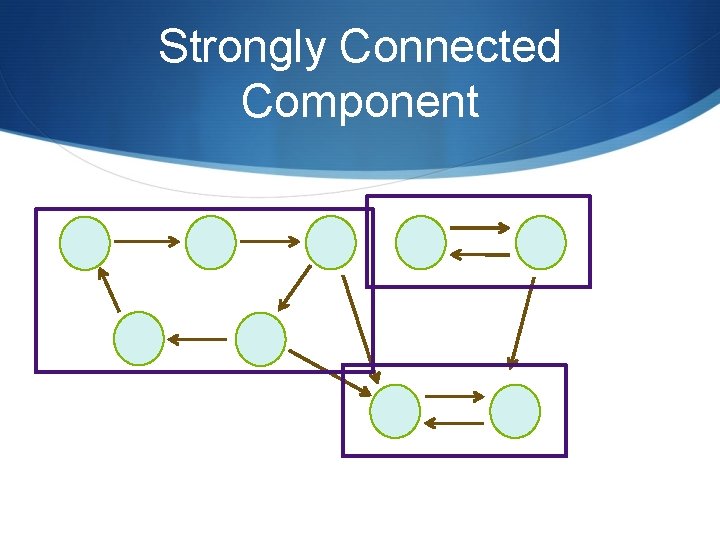
Strongly Connected Component
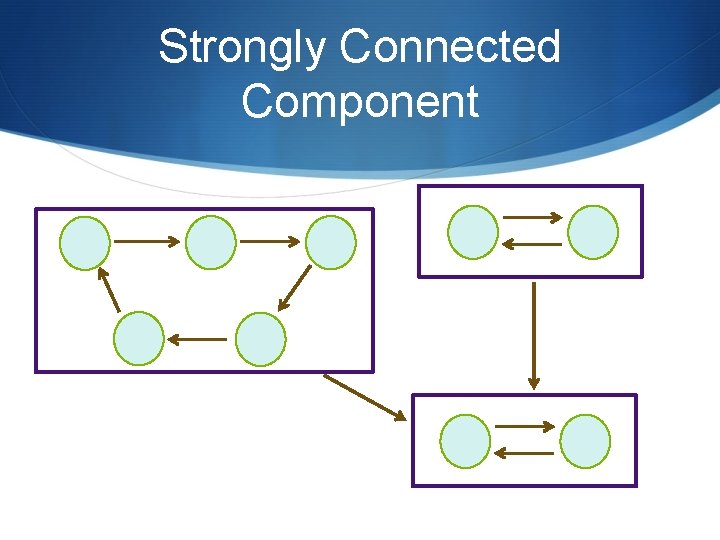
Strongly Connected Component
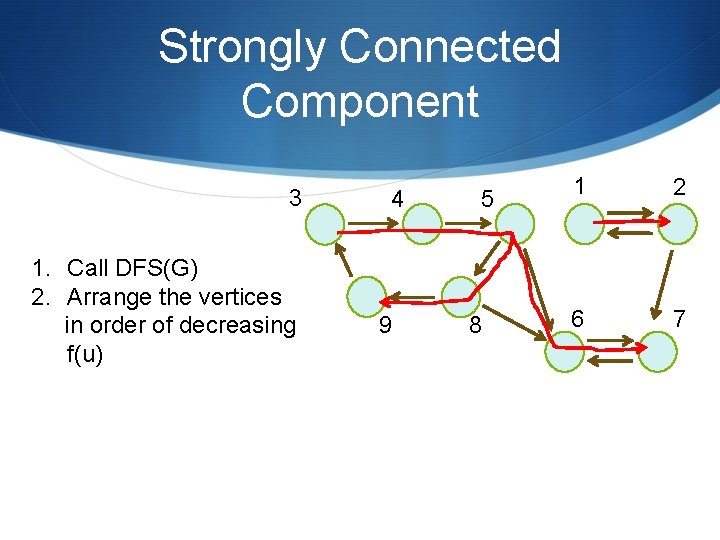
Strongly Connected Component 3 1. Call DFS(G) 2. Arrange the vertices in order of decreasing f(u) 4 9 5 8 1 2 6 7
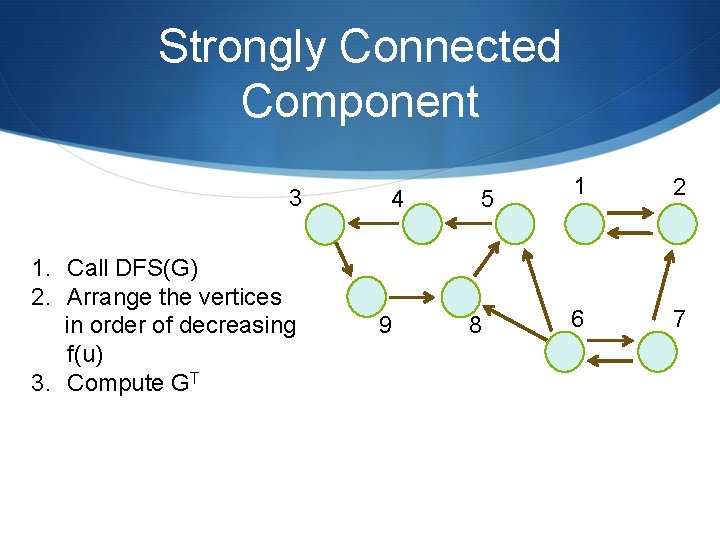
Strongly Connected Component 3 1. Call DFS(G) 2. Arrange the vertices in order of decreasing f(u) 3. Compute GT 4 9 5 8 1 2 6 7
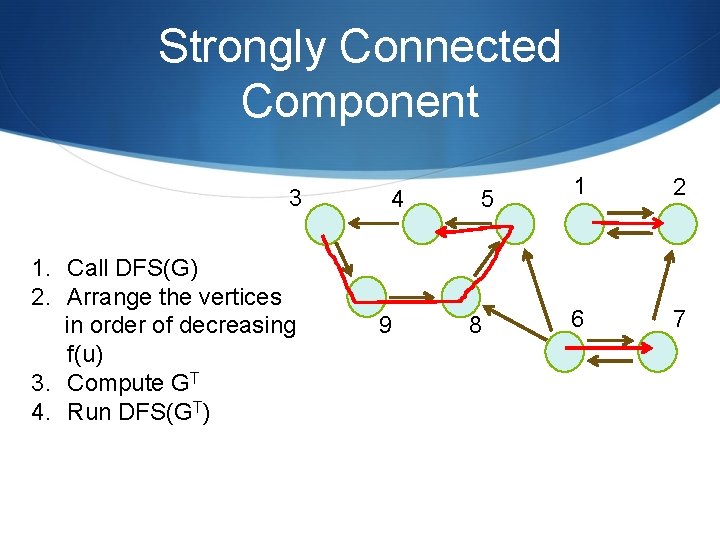
Strongly Connected Component 3 1. Call DFS(G) 2. Arrange the vertices in order of decreasing f(u) 3. Compute GT 4. Run DFS(GT) 4 9 5 8 1 2 6 7
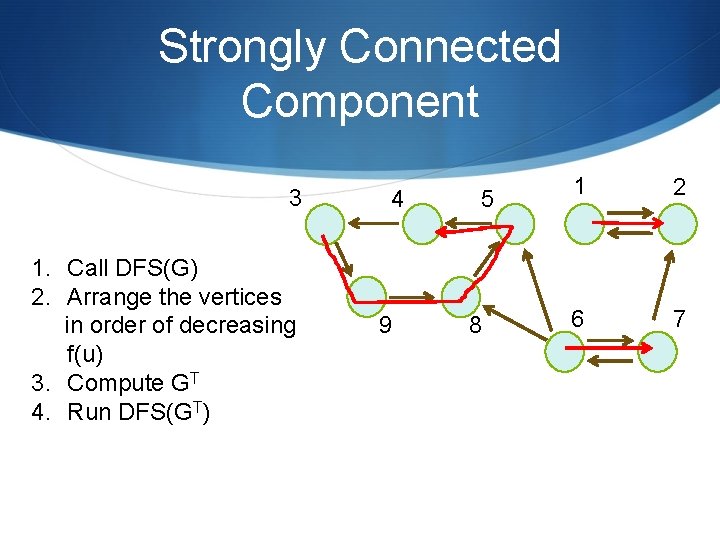
Strongly Connected Component 3 1. Call DFS(G) 2. Arrange the vertices in order of decreasing f(u) 3. Compute GT 4. Run DFS(GT) 4 9 5 8 1 2 6 7
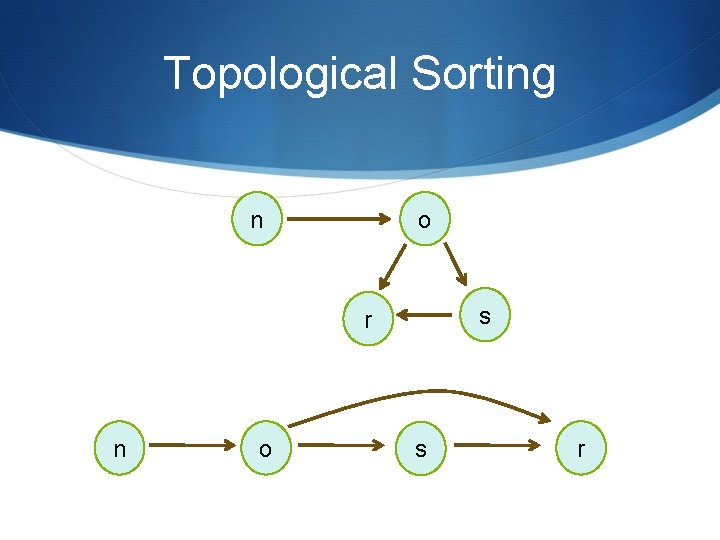
Topological Sorting n o s r
Strongly Connected Component
![Strongly Connected Component Last f[u] > Last f[u] Strongly Connected Component Last f[u] > Last f[u]](http://slidetodoc.com/presentation_image_h/8a8f49c577a55fe058956e0d59d3f823/image-70.jpg)
Strongly Connected Component Last f[u] > Last f[u]
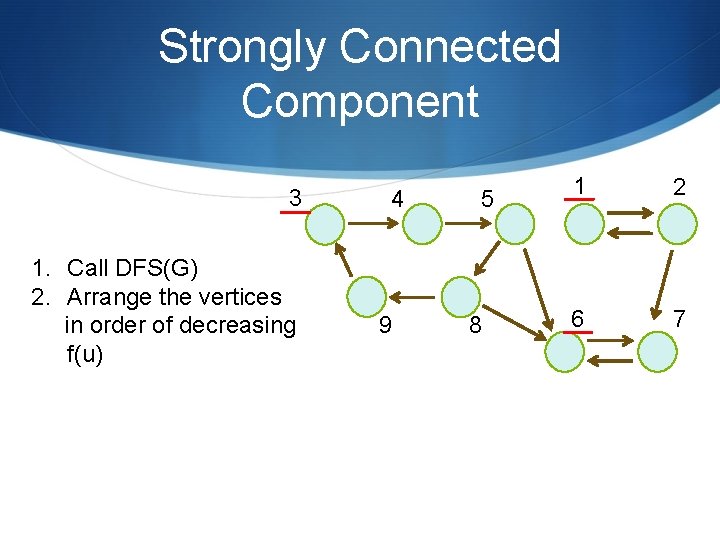
Strongly Connected Component 3 1. Call DFS(G) 2. Arrange the vertices in order of decreasing f(u) 4 9 5 8 1 2 6 7
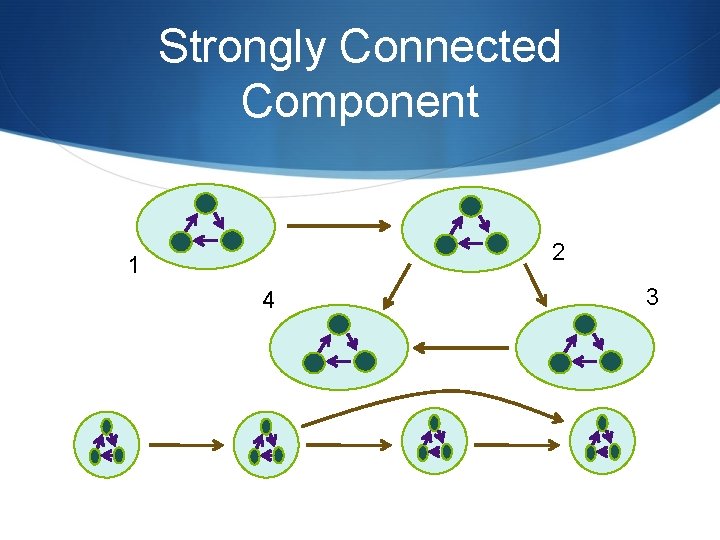
Strongly Connected Component 2 1 4 3
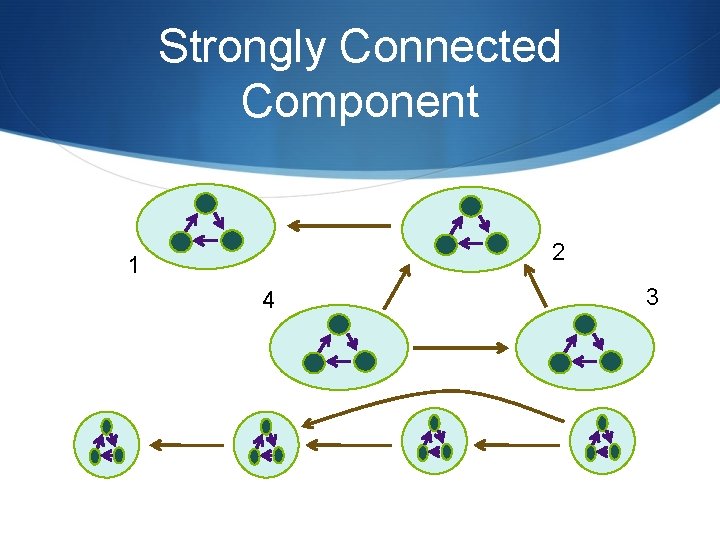
Strongly Connected Component 2 1 4 3
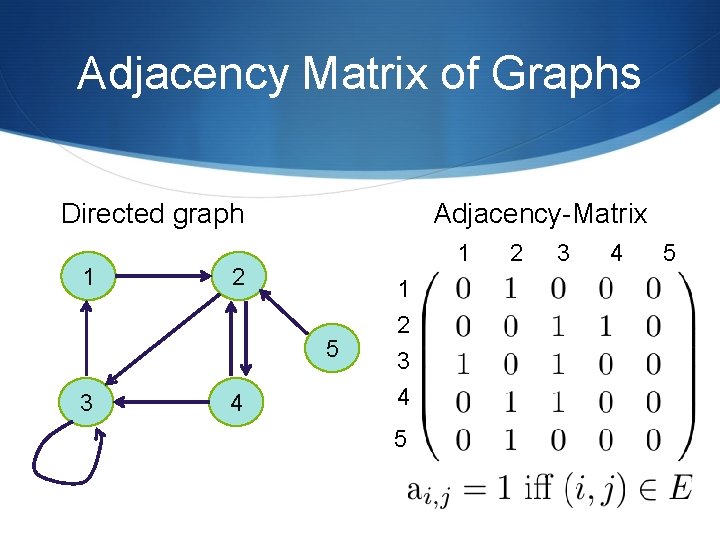
Adjacency Matrix of Graphs Directed graph 1 Adjacency-Matrix 1 2 5 3 4 1 2 3 4 5
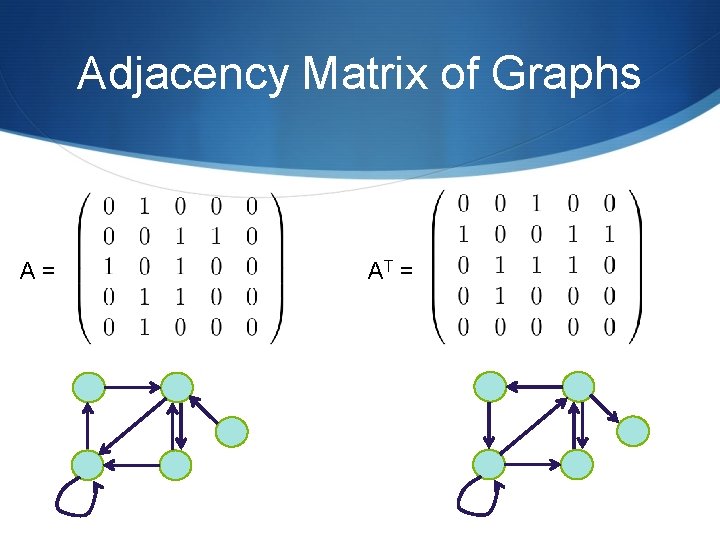
Adjacency Matrix of Graphs A= AT =
- Slides: 75