Graph Revisited Fei Chen CSCI 2100 B Data

Graph Revisited Fei Chen CSCI 2100 B Data Structures Tutorial 12 1

Outline • Graph Adjacency Representation • Topological Sort • Minimum Spanning Tree – Kruskal’s Algorithm – Prim’s Algorithm • Shortest Path – Dijkstra’ Algorithm 2
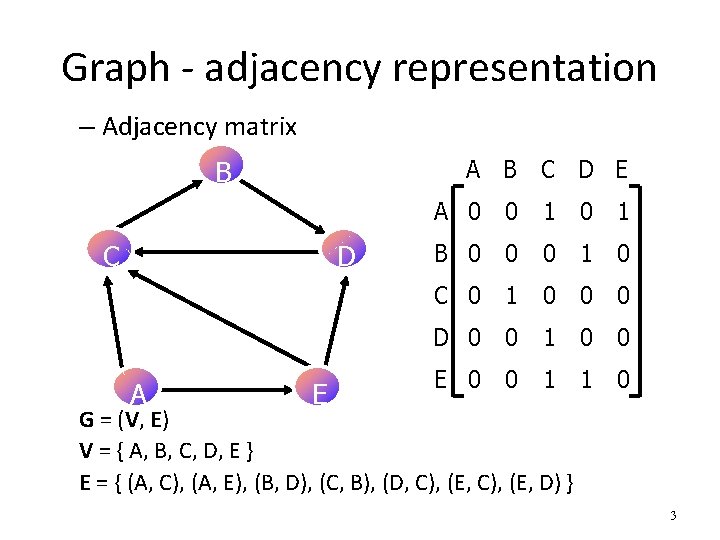
Graph - adjacency representation – Adjacency matrix A B C D E B C D A E A 0 0 1 B 0 0 0 1 0 C 0 1 0 0 0 D 0 0 1 0 0 E 0 0 1 1 0 G = (V, E) V = { A, B, C, D, E } E = { (A, C), (A, E), (B, D), (C, B), (D, C), (E, D) } 3
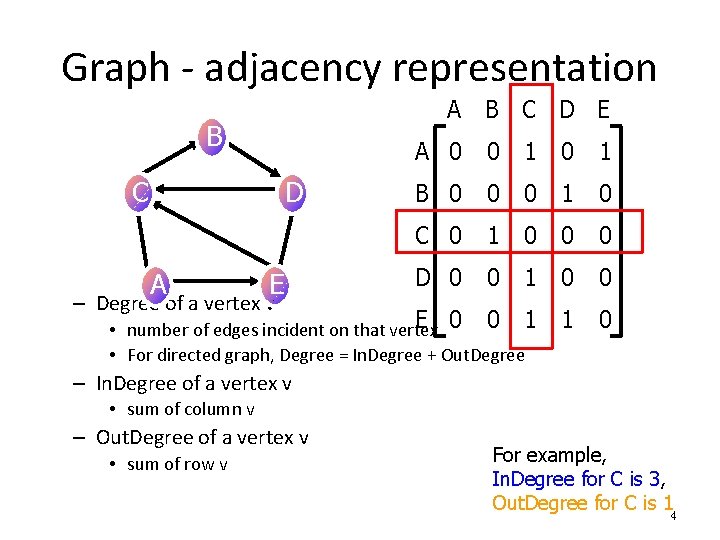
Graph - adjacency representation A B C D E B A 0 0 1 B 0 0 0 1 0 C 0 1 0 0 0 D 0 0 1 0 0 E 0 0 1 • number of edges incident on that vertex • For directed graph, Degree = In. Degree + Out. Degree 1 0 C D A E – Degree of a vertex v – In. Degree of a vertex v • sum of column v – Out. Degree of a vertex v • sum of row v For example, In. Degree for C is 3, Out. Degree for C is 14
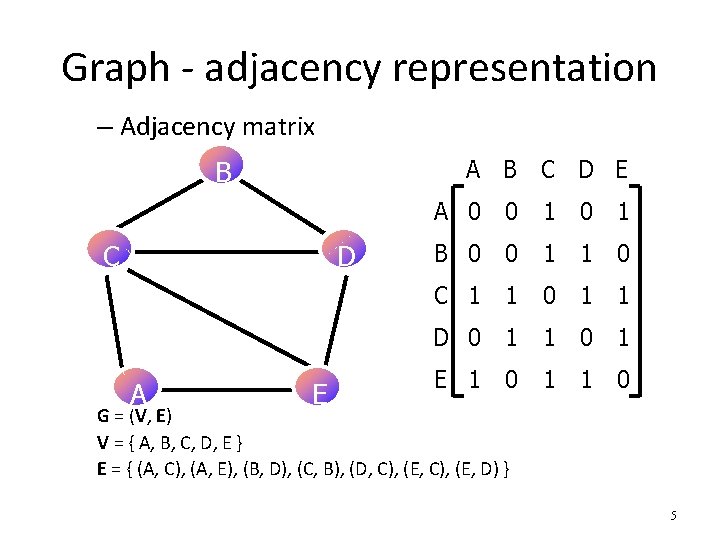
Graph - adjacency representation – Adjacency matrix A B C D E B C D A E A 0 0 1 B 0 0 1 1 0 C 1 1 0 1 1 D 0 1 1 0 1 E 1 0 1 1 0 G = (V, E) V = { A, B, C, D, E } E = { (A, C), (A, E), (B, D), (C, B), (D, C), (E, D) } 5
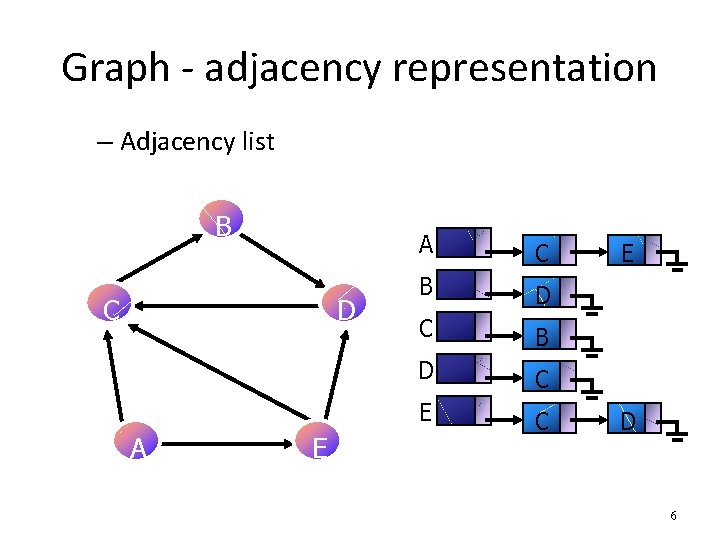
Graph - adjacency representation – Adjacency list B C D A E A C B D C E D 6

Topological Sort • A topological sort of a DAG (Directed Acyclic Graph) G is a linear ordering of all its vertices such that if G contains an edge (u, v), then u appears before v in the ordering. 7
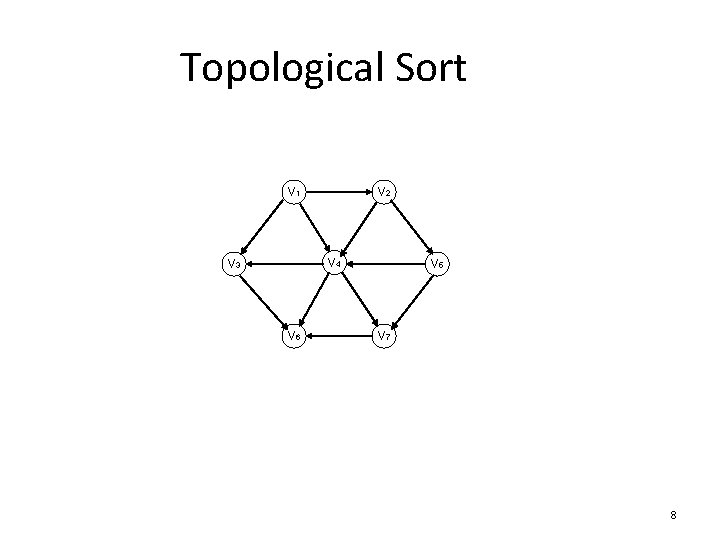
Topological Sort V 1 V 2 V 4 V 3 V 6 V 5 V 7 8

How to find the topological ordering? • Define the indegree of a vertex v as the # of edges (u, v). We compute the indegrees of all vertices in the graph. • Find any vertex with no incoming edges (or the indegree is 0). • We print this vertex, and remove it, along with its edges, from the graph. • Then we apply this same strategy to the rest of the graph. 9
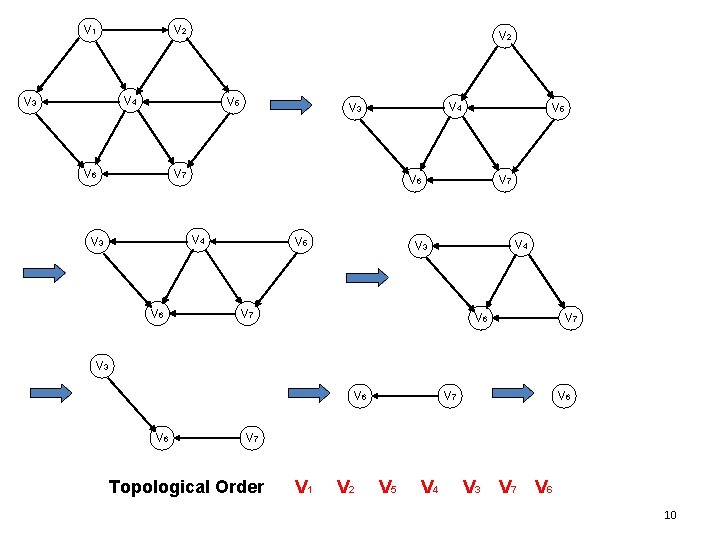
V 1 V 2 V 4 V 3 V 5 V 6 V 4 V 3 V 7 V 6 V 4 V 3 V 6 V 5 V 7 V 4 V 3 V 7 V 6 V 7 V 3 V 6 V 7 Topological Order V 1 V 2 V 5 V 4 V 3 V 7 V 6 10
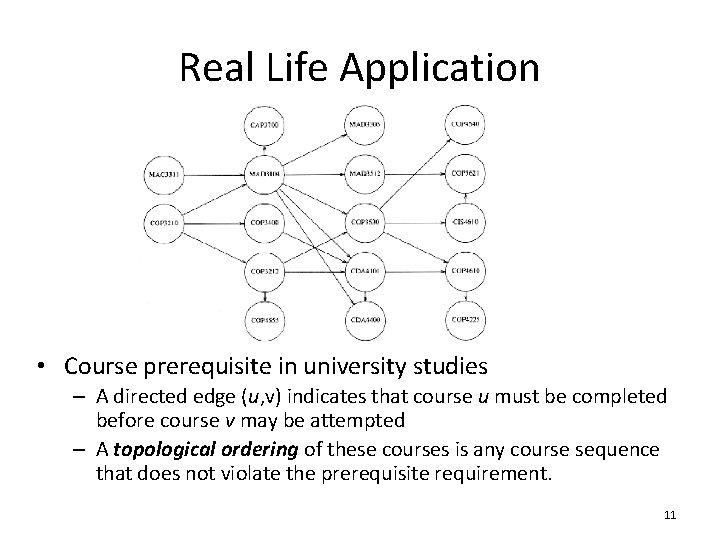
Real Life Application • Course prerequisite in university studies – A directed edge (u, v) indicates that course u must be completed before course v may be attempted – A topological ordering of these courses is any course sequence that does not violate the prerequisite requirement. 11

Notes • Is topological ordering possible with a cyclic graph? – No, since for two vertices v and w on the cycle, v precedes w and w precedes v. • Is the ordering unique? – It is not necessarily unique; any legal ordering will do (e. g. , v 1, v 2, v 5, v 4, v 3, v 7, v 6 and v 1, v 2, v 5, v 4, v 7, v 3, v 6 are topological orderings). 12
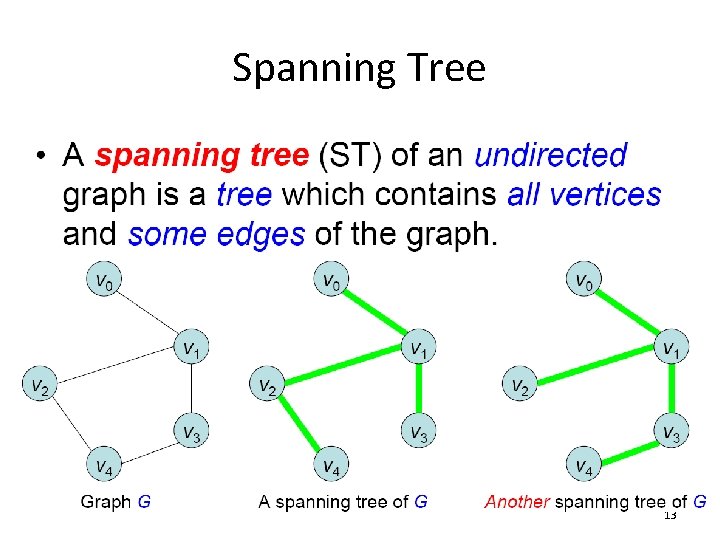
Spanning Tree 13
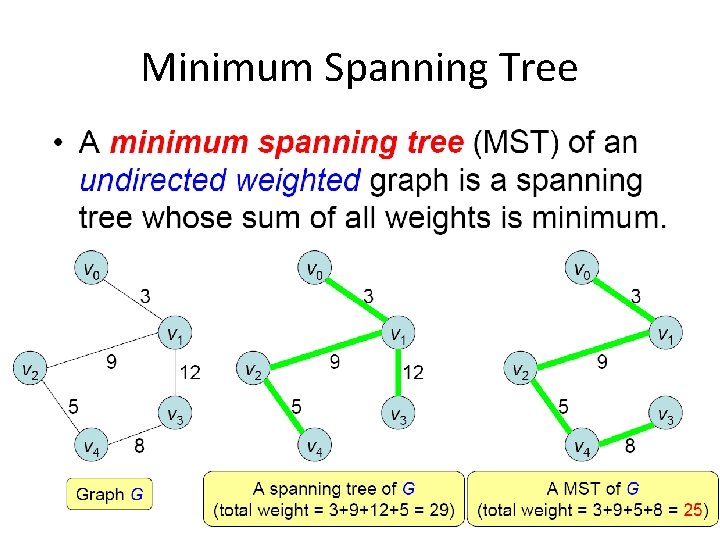
Minimum Spanning Tree 14
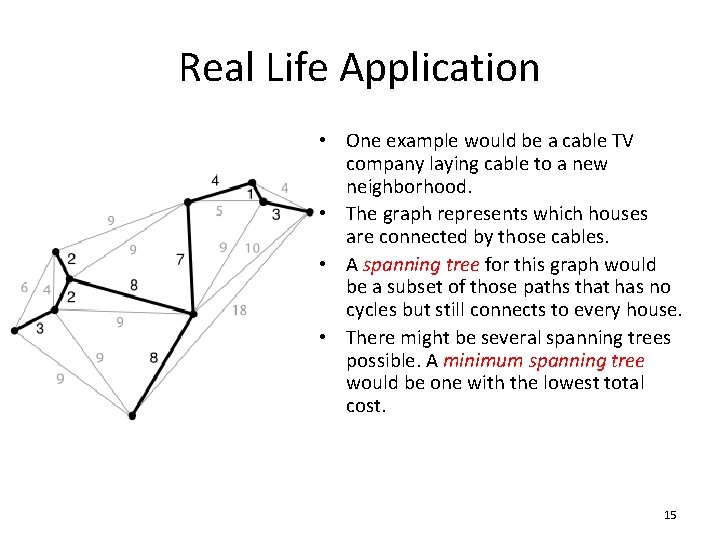
Real Life Application • One example would be a cable TV company laying cable to a new neighborhood. • The graph represents which houses are connected by those cables. • A spanning tree for this graph would be a subset of those paths that has no cycles but still connects to every house. • There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost. 15

MST Algorithm 16
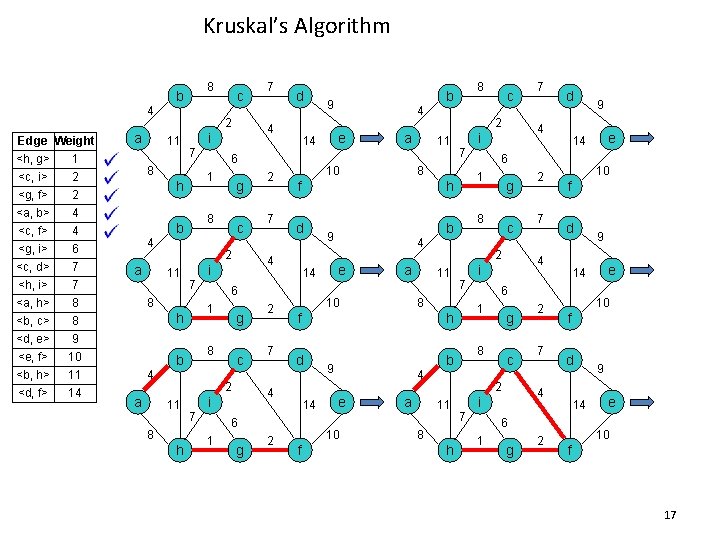
Kruskal’s Algorithm 8 b 4 Edge Weight <h, g> 1 <c, i> 2 <g, f> 2 <a, b> 4 <c, f> <g, i> <c, d> <h, i> <a, h> 4 6 7 7 8 <b, c> <d, e> <e, f> <b, h> <d, f> 8 9 10 11 14 a 2 11 7 4 c 2 11 7 g 8 b 4 c 2 11 8 h 7 7 g 2 a 11 d b 9 a 10 h d b 9 10 f a c 7 8 h 7 1 g 8 c f d 7 g 2 e 10 f d 14 6 1 9 14 4 i 7 2 e 10 6 2 11 2 9 14 4 i 4 e g 8 8 f 14 1 2 11 d 6 4 e 14 7 7 4 i 8 h 6 1 e c 2 f 4 i 7 2 4 10 6 1 h 2 8 b 9 14 4 i 8 a g 8 b d 6 1 h 7 4 i 8 a c 9 e 10 f 17
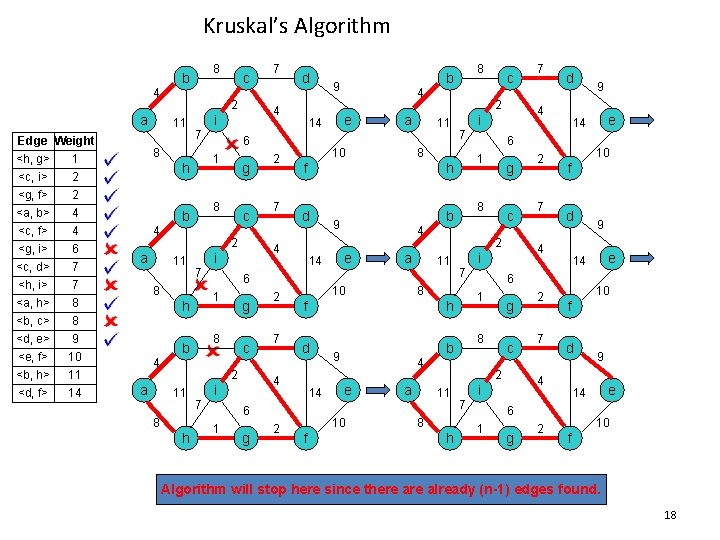
Kruskal’s Algorithm 8 b 4 a Edge Weight <h, g> 1 <c, i> 2 <g, f> 2 <a, b> 4 <c, f> <g, i> <c, d> <h, i> <a, h> 4 6 7 7 8 <b, c> <d, e> <e, f> <b, h> <d, f> 8 9 10 11 14 2 11 7 4 c 2 11 7 g 8 b 4 c 2 11 8 h 7 7 g 2 a 11 d b 9 a 10 h d b 9 10 f a c 7 8 h 7 1 g 8 c f d 7 g 2 e 10 f d 9 e 14 6 1 9 14 4 i 7 2 e 10 6 2 11 2 9 14 4 i 4 e g 8 8 f 14 1 2 11 d 6 4 e 14 7 7 4 i 8 h 6 1 e c 2 f 4 i 7 2 4 10 6 1 h 2 8 b 9 14 4 i 8 a g 8 b d 6 1 h 7 4 i 8 a c 10 f Algorithm will stop here since there already (n-1) edges found. 18

19
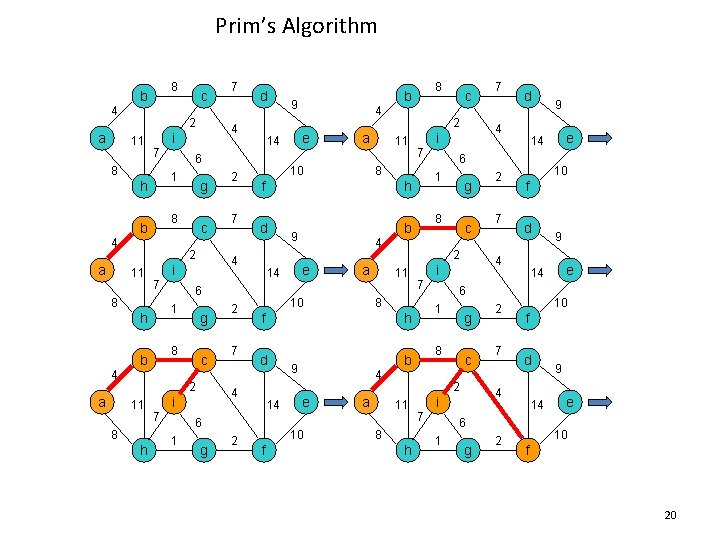
Prim’s Algorithm 8 b 4 a 2 11 7 4 c 2 11 7 g 8 b 4 c 2 11 8 h 7 7 g 2 a 11 d b 9 a 10 h d b 9 10 f a c 7 8 h 7 1 g 8 c f d 7 g 2 e 10 f d 14 6 1 9 14 4 i 7 2 e 10 6 2 11 2 9 14 4 i 4 e g 8 8 f 14 1 2 11 d 6 4 e 14 7 7 4 i 8 h 6 1 e c 2 f 4 i 7 2 4 10 6 1 h 2 8 b 9 14 4 i 8 a g 8 b d 6 1 h 7 4 i 8 a c 9 e 10 f 20
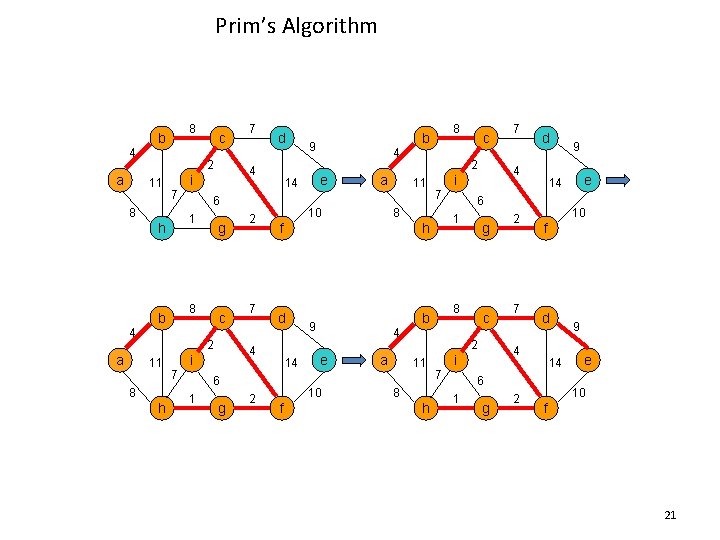
Prim’s Algorithm 8 b 4 a 2 11 7 g 8 b 4 c 2 11 8 h d 7 g 2 e a 11 h d b 14 e a 1 g 8 c 2 11 8 h d 7 f d 14 6 1 g 2 e 10 4 i 7 2 9 14 6 4 10 f 7 7 4 i 8 9 c 2 f 6 1 4 10 4 i 7 2 8 b 9 14 6 1 h 7 4 i 8 a c 9 e 10 f 21

22
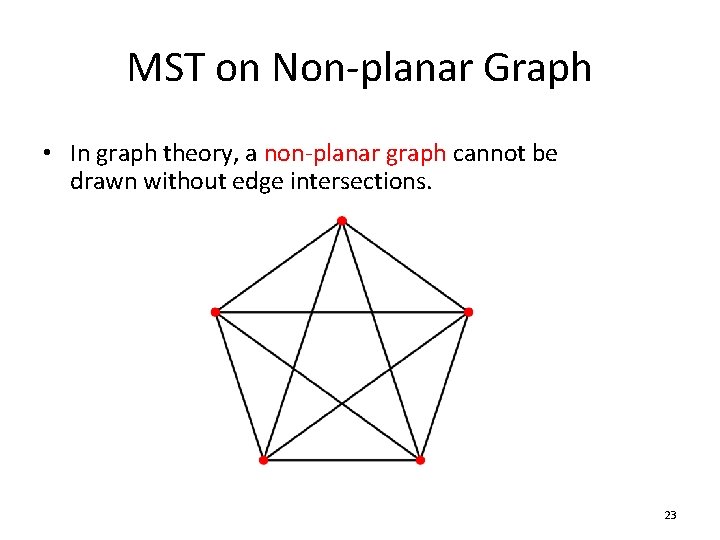
MST on Non-planar Graph • In graph theory, a non-planar graph cannot be drawn without edge intersections. 23
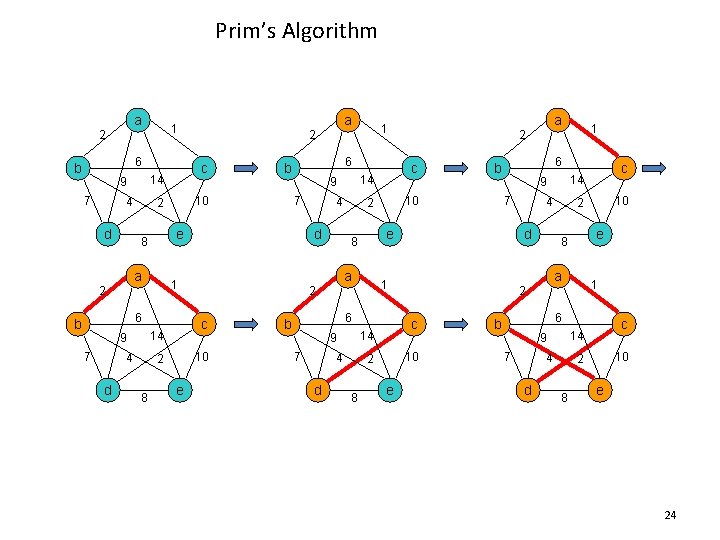
Prim’s Algorithm a 6 b 7 4 d 10 2 a 7 4 d 10 2 8 e 7 4 d 8 e e 8 a 10 2 1 2 c 14 4 d 1 6 9 7 c 14 9 e 8 a b 6 b 10 2 2 c 14 4 d 1 6 9 7 1 2 c 14 9 e 8 2 b 6 b a 1 2 c 14 9 a 1 2 6 b 7 4 d c 14 9 10 2 8 e 24
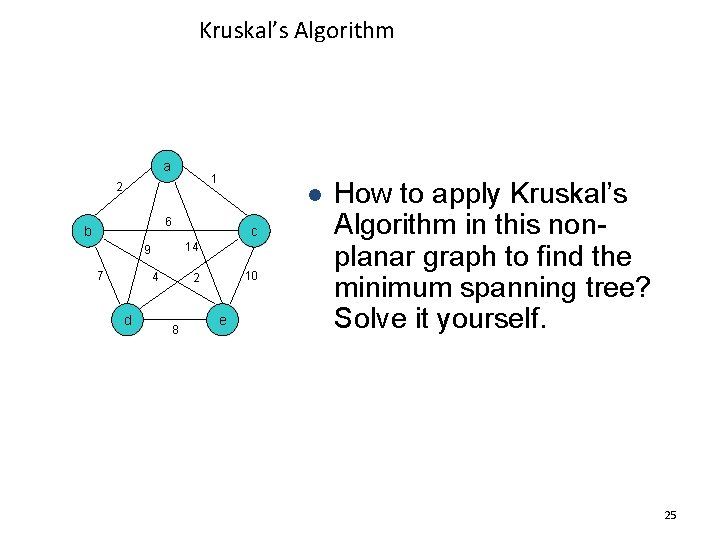
Kruskal’s Algorithm a 1 2 l 6 b c 14 9 7 4 d 10 2 8 e How to apply Kruskal’s Algorithm in this nonplanar graph to find the minimum spanning tree? Solve it yourself. 25
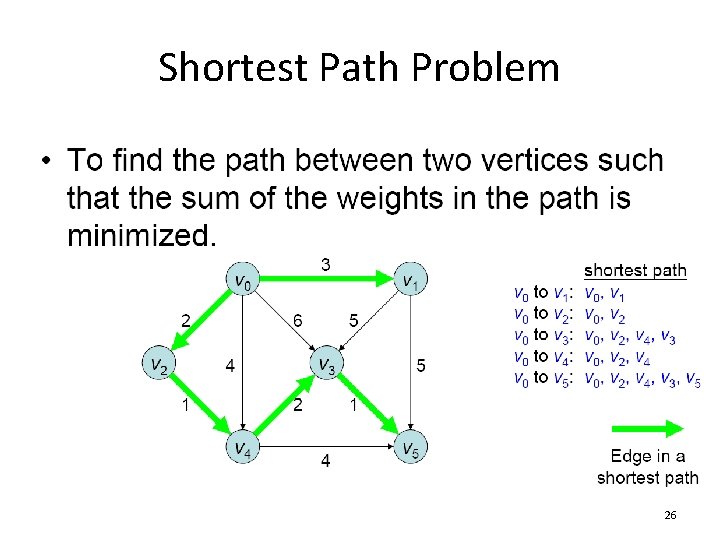
Shortest Path Problem 26
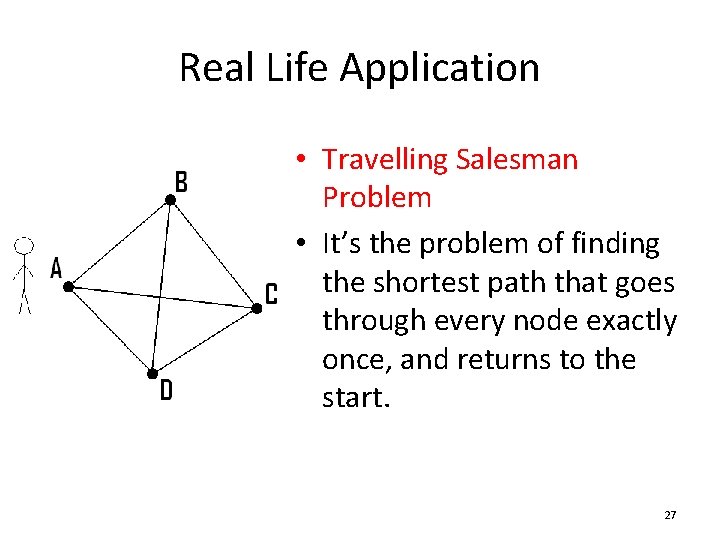
Real Life Application • Travelling Salesman Problem • It’s the problem of finding the shortest path that goes through every node exactly once, and returns to the start. 27
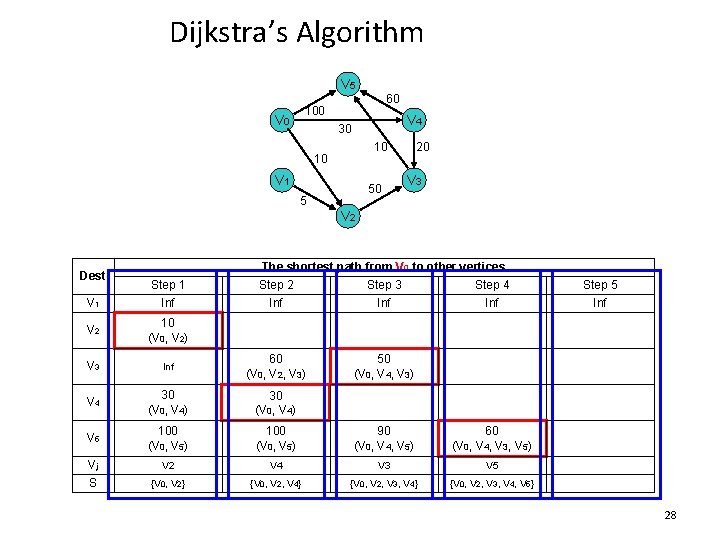
Dijkstra’s Algorithm V 5 60 100 V 4 30 10 10 V 1 50 5 20 V 3 V 2 Dest V 1 Step 1 Inf The shortest path from V 0 to other vertices Step 2 Step 3 Step 4 Inf Inf V 2 10 (V 0, V 2) V 3 Inf 60 (V 0, V 2, V 3) V 4 30 (V 0, V 4) V 5 100 (V 0, V 5) 90 (V 0, V 4, V 5) 60 (V 0, V 4, V 3, V 5) V 2 V 4 V 3 V 5 {V 0, V 2} {V 0, V 2, V 4} {V 0, V 2, V 3, V 4, V 5} Vj S Step 5 Inf 50 (V 0, V 4, V 3) 28

29
- Slides: 29