Graph Reconstruction Conjecture Graph Reconstruction Conjecture Proposed by

Graph Reconstruction Conjecture

Graph Reconstruction Conjecture Proposed by S. M. Ulan & P. J. Kelly in 1941: The conjecture states that every graph with at least 3 vertices is reconstructible; a graph G is reconstructible if it is defined by its vertexdeleted subgraphs.

Definitions v 1 v 2 G= v 4 v 3 DECK = the multi-subset of vertex-deleted subgraphs of G v 2 v 1 v 2 D(G) = v 4 v 3 CARD = a vertex-deleted subgraph of G (we do not worry about graphs that are different through labelling nodes differently, but are isomorphic)

Graph reconstruction Can we obtain G from D(G)? D(G) =

Graph reconstruction Can we obtain G from D(G)? D(G) = G=

Graph Reconstruction Conjecture Every graph with at least three vertices is reconstructible n Unproven n Verified for regular graphs (graphs in which all vertices have same number of edges). n Verified for all graphs with at most 11 vertices. n Bollobás: Used probability to show that almost all graphs are reconstructible; probability that a randomly chosen graph with n vertices is not reconstructible approaches zero as n approaches infinity. n For almost all graphs, there exist 3 cards that uniquely determine the graph.

Reconstruction Number rn(G) n n The number of cards required to reconstruct the original graph. > 2 because at least 2 different graphs can be generated from a deck of 2 (difference between the 2 graphs is 1 edge)

Reconstruction Number Logic 1. 2. 3. Get all cards of a given deck Extend the cards The intersection of the extended cards is the solution Conjecture: rn(G) is at most (n/2 +1) 1. Bollobás used proof via probability to prove rn(G) is at least 3

Finding Reconstruction Number v 1 v 2 G= v 4 1. v 3 Get all cards of a given deck v 2 v 4 D(G) = v 4 v 3 v 1 v 2 v 3

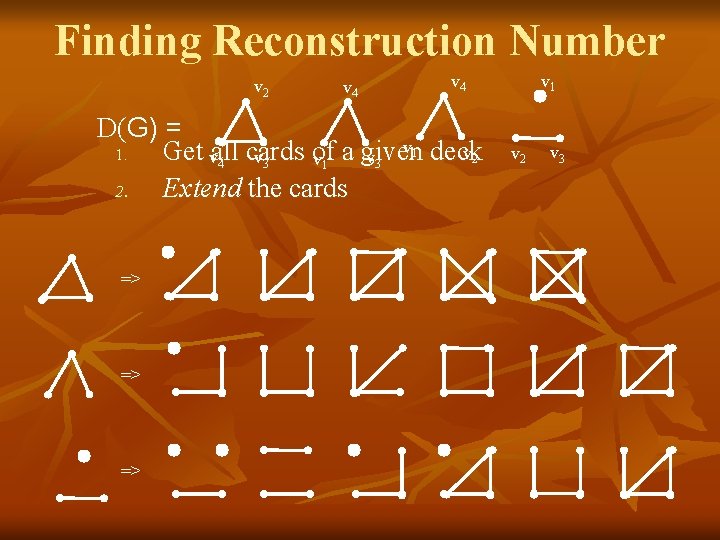
Finding Reconstruction Number v 2 v 4 D(G) = v 1 deck v 2 1. Get vall cards of v 3 v 1 a given 4 2. Extend the cards => => => v 1 v 2 v 3

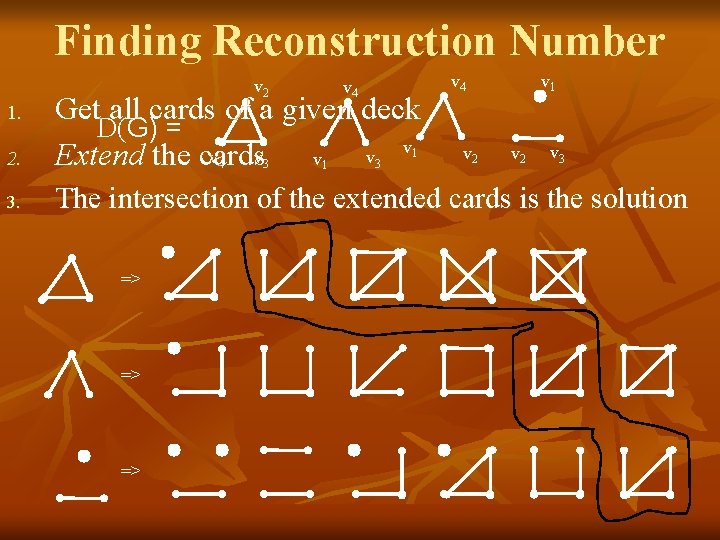
Finding Reconstruction Number v 2 v 4 v 1 2. Get all cards of a given deck D(G) = v v Extend the cards v 3. The intersection of the extended cards is the solution 1. 4 => => => 3 1 v 2 v 3

Proven generally not reconstructible: n n n Digraphs (AKA Directed graph) Hypergraphs: edges can connect to any number of vertices. Infinite Graphs: Infinitely many vertices and/or edges