Graph Partitioning Problem Partition the graph into P

Graph Partitioning Problem • Partition the graph into P (number of processors) parts such that: (a) each partition has equal number of enodes to within one (i. e. we achieve load balance among processors) (b) the partition boundary size is minimized (we reduce expensive communication cost) Can Özturan

Graph Partitioning • Look at bisection problem, i. e. P = 2 • Edge Separator: if removed breaks the graph into two parts with no edges connecting them • Vertex separator Can Özturan 2

Partitioning • Several heuristics have been proposed: – Kernighan-Lin – geometric methods: e. g. Orthogonal Recursive bisection, Moment of Inertia Recursive bisection – Reordering Based (profile minimization): – Spectral Partitioner: (high quality) uses “Laplacian matrix” of the graph and uses the eigenvector corresponding to 2 nd smallest eigenvalue – Multi-level methods: coarsens the graph to get a smaller graph • Software Packages available: Chaco, METIS Can Özturan

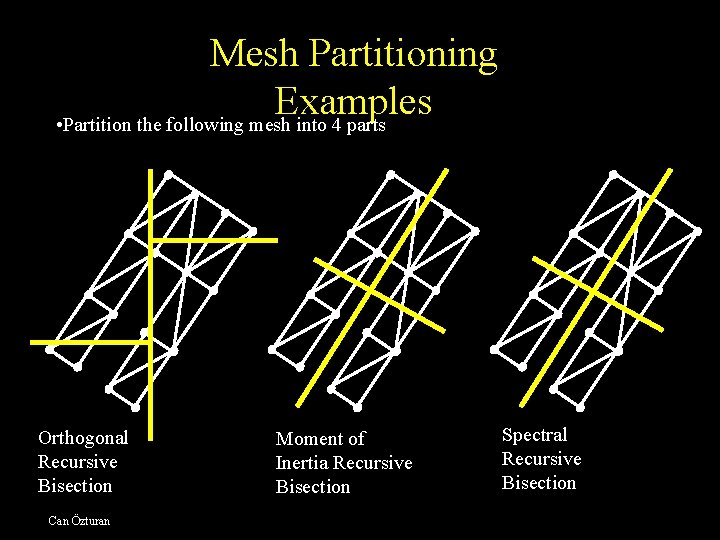
Mesh Partitioning Examples • Partition the following mesh into 4 parts Orthogonal Recursive Bisection Can Özturan Moment of Inertia Recursive Bisection Spectral Recursive Bisection

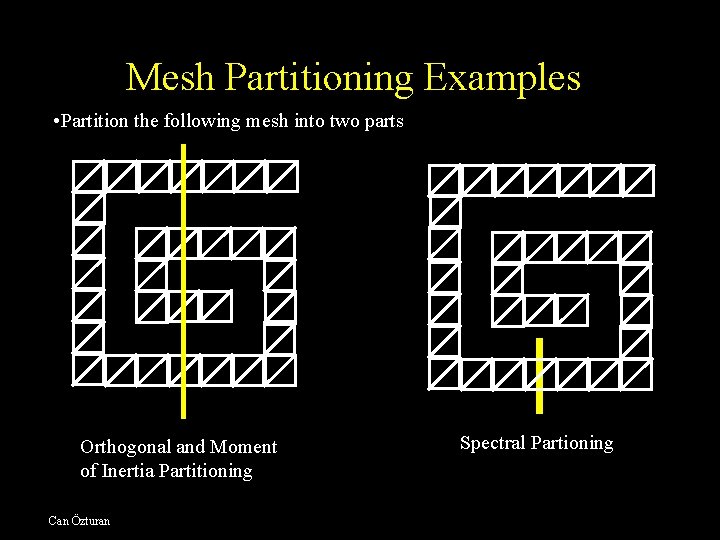
Mesh Partitioning Examples • Partition the following mesh into two parts Orthogonal and Moment of Inertia Partitioning Can Özturan Spectral Partioning

Spectral Graph Partitioning • Laplacian matrix of an undirected graph is defined as: L ij = d i if i = j (degree of each node) 0 if nodes i and j are not adjacent 1 if nodes i and j are adjacent 1 5 2 3 1 Can Özturan 4 L= 6 2 3 4 5 6 1 2 -1 -1 0 0 0 2 -1 3 -1 0 3 -1 -1 3 -1 0 0 4 0 0 -1 3 -1 -1 5 0 -1 3 -1 6 0 0 0 -1 -1 2 6

Spectral Graph Partitioning • Another way to obtain the Laplacian matrix is: - direct the edges of the graph arbitrarily - Let C denote the |V| x |E| vertex incidence matrix, then we have: Cve = +1 -1 0 if v is the head of e if v is the tail of e Otherwise • We then have: L = C CT Can Özturan 7

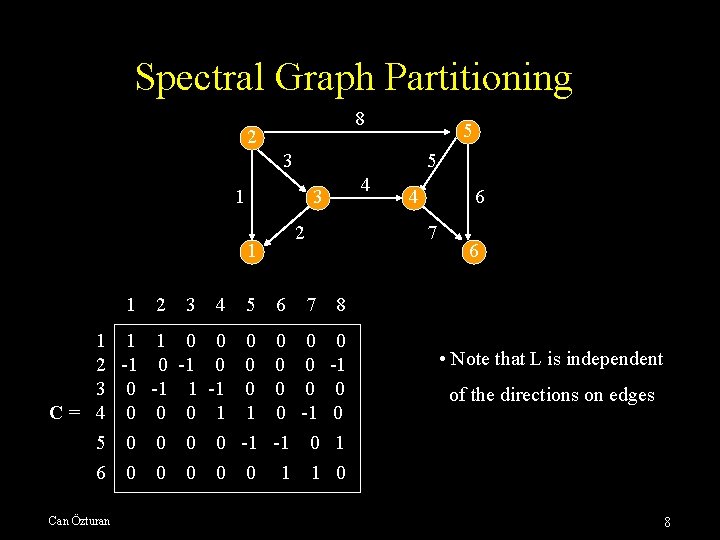
Spectral Graph Partitioning 8 2 5 3 5 1 2 1 1 2 3 1 1 1 0 2 -1 0 -1 3 0 -1 1 C= 4 0 0 0 5 0 0 0 6 0 0 0 Can Özturan 4 4 3 5 4 6 7 8 0 0 0 -1 0 0 1 1 0 0 -1 -1 0 0 0 -1 0 0 1 0 6 • Note that L is independent of the directions on edges 8

Spectral Graph Partitioning • We can show : T T T x L x = x C C x = ( C x) ( CT x) = (x v - 2 xw) (v, w) E Can Özturan 9

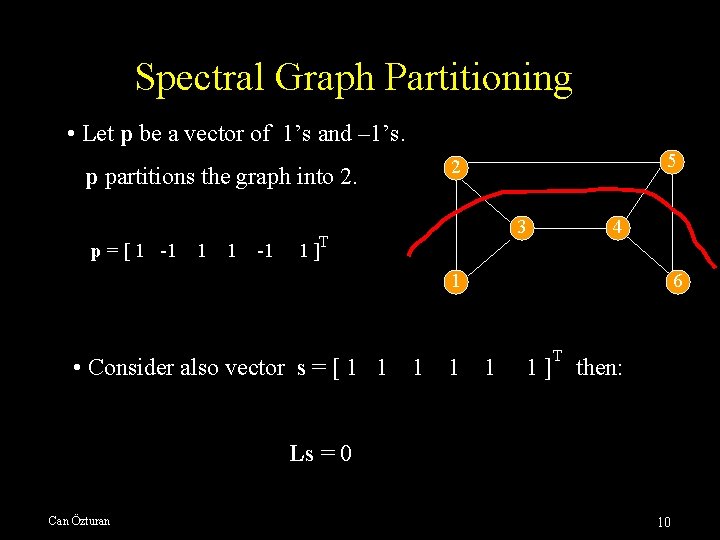
Spectral Graph Partitioning • Let p be a vector of 1’s and – 1’s. p partitions the graph into 2. p = [ 1 -1 1 1 -1 5 2 3 T 4 1] 1 • Consider also vector s = [ 1 1 1 6 1] T then: Ls = 0 Can Özturan 10

Spectral Graph Partitioning • Objectives: divide the graph into two parts such that: (1) We have load balance: p. T s = 0 (2) Number of edges cut is minimized: T p L p = (p (v, w) E Can Özturan v- p w ) 2 = 4 (num. of edges cut) 11

Spectral Graph Partitioning • Problem Statement p. T L p Min pi = + 1 p = 0 i integer version NP-hard Can Özturan p. T L p Min p R i p p 2 = n i i = 0 real version 12

Spectral Graph Partitioning • Since Ls = 0 , then λ 1 = 0 is an eigenvalue of L • It is the smallest eigenvalue of L (use Gerschgorin circle theorem) λ 1 = 0 < λ 2 = …. <= λ n • Since L is symmetric, it has complete set of real eigenvalues which can be orthogonalized with each other • Express p as a linear combination of normalized eigenvectors n p = i=2 Can Özturan ci vi where || vi ||2 = 1 13

Spectral Graph Partitioning T • Solution, i. e. p L p is minimized when p is selected as: q = c’ 2 v 2 • Proof: we can show that: p. T L p - q. T L q 0 (1) as follows: Lp = λ 2 c 2 v 2 + λ 3 c 3 v 3 + …. + λn cn vn T p Lp = Can Özturan 2 λ 2 c 2 + λ 3 2 c 3 + …. + 2 λn cn 14

Spectral Graph Partitioning • Since p. T p = n and vi are normalized: c 22 + c 23 + …. + c 2 n = n (1) becomes: 2 (λ 2 c 2 2 + 2 λ 3 c 3 + …. + 2 2 λ nc n) 2 - λ 2 n 2 2 2 (λ 2 c 2 + λ 3 c 3 + …. + λ nc n) - λ 2 ( c 2 + c 3 + … + c n ) 2 (λ 3 - λ 2 ) c 3 + … + (λ n - λ 2 ) c 2 n 0 Can Özturan Q. E. D. 15

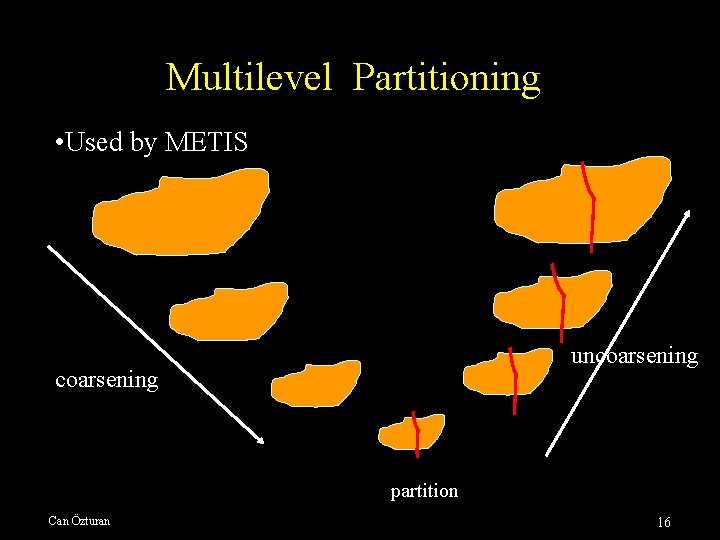
Multilevel Partitioning • Used by METIS uncoarsening partition Can Özturan 16