Graph Orientability and Its Application to Mathematical Modeling

Graph Orientability and Its Application to Mathematical Modeling in the Social Sciences Carmen Frerichs 252 a-ao December 14, 2000

Orientability ØWhat is orientability? ØHow is orientation in a graph determined? ØHow do you give a graph the property of orientability? ØA naïve algorithm ØAnalysis of algorithm

What is orientability? The concept of orientability in graphs was developed as a means of mathematically modeling traffic flow problems. Orientability can only be determined in directed graphs. Essentially, orientability in a graph answers the question is there a way to give each edge in a graph G a direction, or an orientation, so that it is possible to get from any vertex u to every other vertex v.

The concept of orientation is best illustrated using the traffic flow problem that it was designed to model… Given a network of two-way streets in a city, under what circumstances can we make each street oneway in such a way that it is possible to travel from any location to any other. Translating this problem into graph theory, we draw a graph G taking as vertices locations in the city and joining them by an edge if and only if they are connected by a two way street.

We encountered the concept of being able to get from any vertex in a graph to any other vertex in the graph earlier in the semester. This property is that of strong connectivity. Therefore, the orientability of a graph is determined by a. ) whether the graph is strongly connected and b. ) can an orientation (direction) be assigned to each of the edges in the graph while still maintaining this property of strong connectivity.

Graphical representation of traffic flow problem: G = (V, E) V = {a, b, c, d, e, f, g, h, i, j, k} (locations in the city) E = { {a, b}, {a, d}, {b, c}, {b, d}, {c, e}, {d, e}, {e, f}, {e, g}, {e, j}, {e, k}, {f, g}, {f, h}, {f, i}, {g, h}, {h, i}, {j, k} } (two way streets between locations in the city)
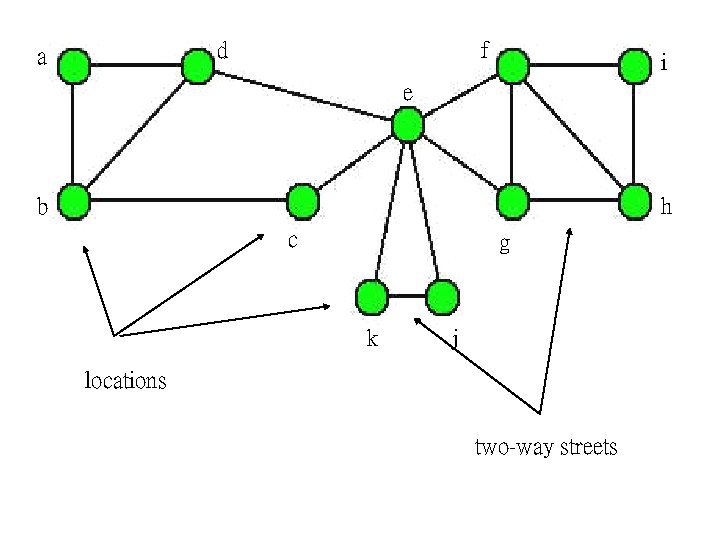
d a f i e b h c g k j locations two-way streets

Naïve algorithm for determining whether or not a strongly connected orientation of graph G is possible: 1. Determine if graph G is strongly connected. 2. Attempt to assign an orientation (direction) to each of the edges in G while maintaining the property of strong connectivity.

1. Determining if G is strongly connected To determine strong connectivity in an undirected graph, the notion of a bridge is introduced. A bridge is an edge {u, v} in a graph G with the property that if the edge {u, v} (but not the vertices u and v) is removed the graph G becomes disconnected.
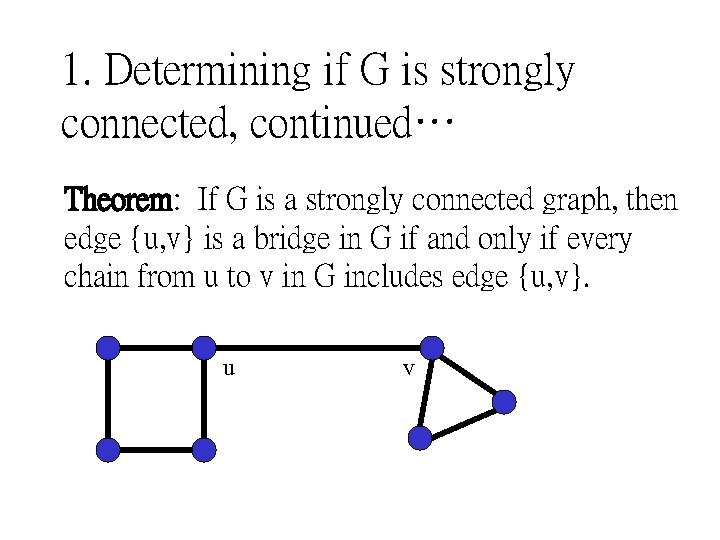
1. Determining if G is strongly connected, continued… Theorem: If G is a strongly connected graph, then edge {u, v} is a bridge in G if and only if every chain from u to v in G includes edge {u, v}. u v

1. Determining if G is strongly connected, continued… From this theorem, we now need to design an algorithm that will test each edge in graph G to determine if it is a bridge. If there are no bridges then G is strongly connected. As it turns out, in the process of assigning orientation (direction) to each of the edges in G (step 2 of the naïve algorithm) we can simultaneously determine whether or not G was a strongly connected graph. So, proceeding to the 2 nd step…

2. Assigning orientation (while maintaining assumed strong connectivity). a. ) pick any vertex and label it 1. b. ) pick any neighbor of the newly labeled vertex 1, label the neighbor 2 and orient the edge between {1, 2} from 1 to 2. c. ) pick any unlabeled neighbor of 2, label it 3 and orient the edge between {2, 3} from 2 to 3.

2. Assigning orientation (while maintaining assumed strong connectivity) continued… d. ) repeat step c. until there are no more unlabeled neighbors. When there are no more unlabeled neighbors for a given vertex, back up to the last vertex with an unlabeled neighbor and proceed from there. e. ) when there are no unlabeled vertices left in G, stop.
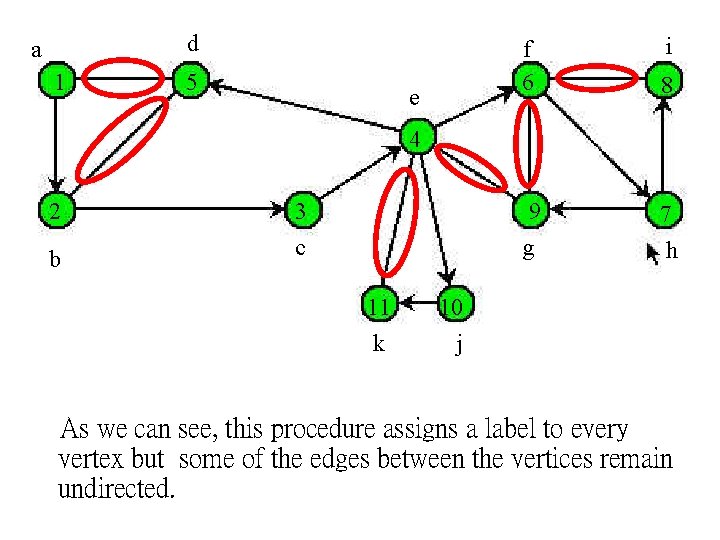
d a 1 5 e i f 6 8 9 g 7 h 4 2 b 3 c 11 k 10 j As we can see, this procedure assigns a label to every vertex but some of the edges between the vertices remain undirected.

2. Assigning orientation (while maintaining assumed strong connectivity) continued… f. ) orient the remaining undirected edges between the now labeled vertices by assigning direction from the vertex with the greater numerical value to the vertex of lesser numerical value.
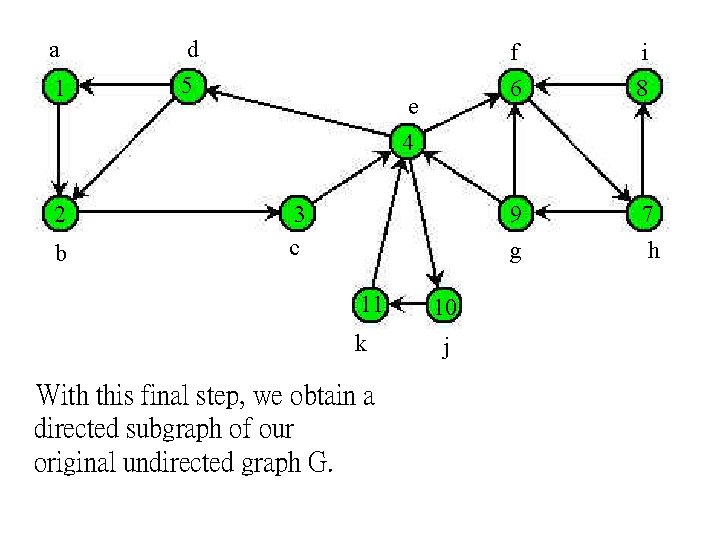
a 1 2 b d 5 e 4 3 c 11 k With this final step, we obtain a directed subgraph of our original undirected graph G. 10 j f i 6 8 9 g 7 h

Some observations This algorithm has essentially performed a Depth First Search on an undirected graph while simultaneously assigning orientation or direction to the edges in the graph. The result of this algorithm is in fact a Depth First Spanning Tree. By evaluating the edges in the resulting spanning tree, we can determine if G was a strongly connected graph.
A Depth First Spanning Tree, T, is the result of the algorithm to determine orientability performed on the original graph G. 1 2 3 4 5 6 10 7 8 11 9

Analysis of algorithm Ø Running time for DFS = O(n+m) Ø Running time for part e. of algorithm (assigning orientability to undirected edges) = O(m)
- Slides: 19