Graph Matching Ilchae Jung Introduction of graph matching

Graph Matching Ilchae Jung

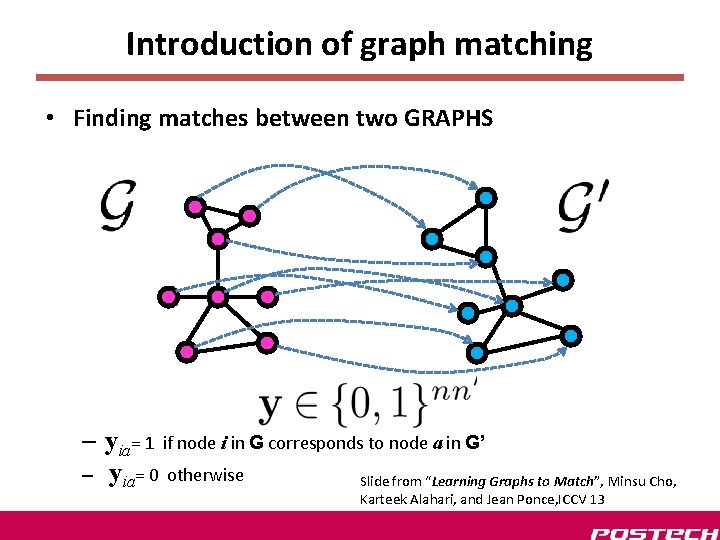
Introduction of graph matching • Finding matches between two GRAPHS – yia= 1 if node i in G corresponds to node a in G’ – yia= 0 otherwise Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

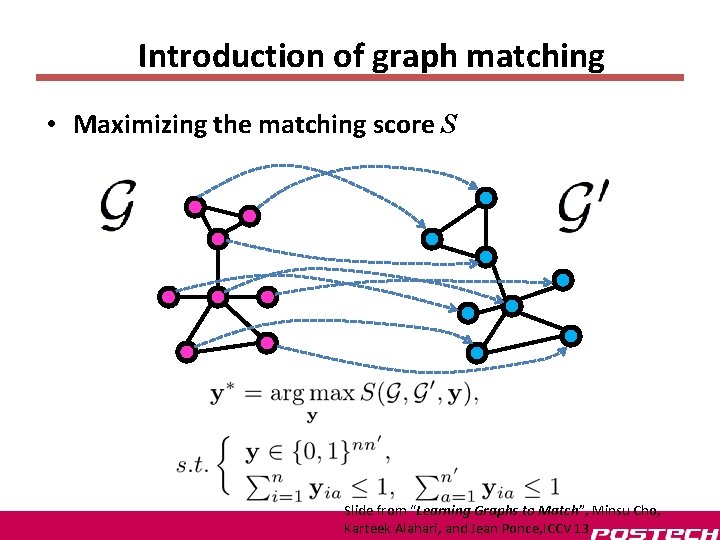
Introduction of graph matching • Maximizing the matching score S Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

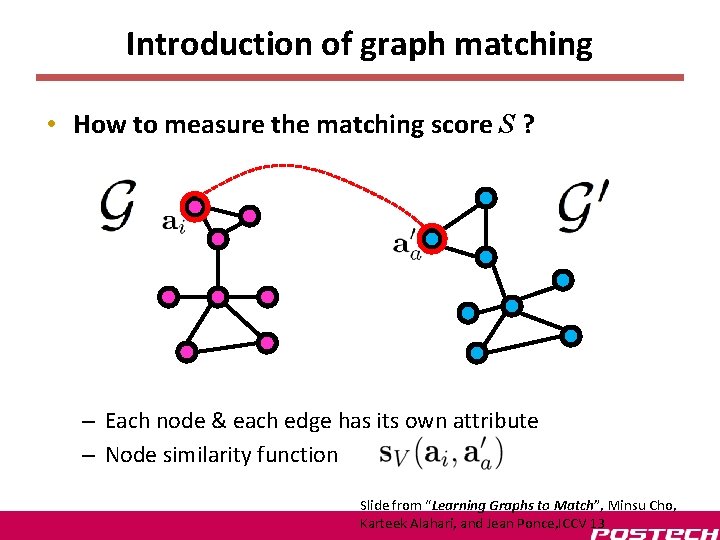
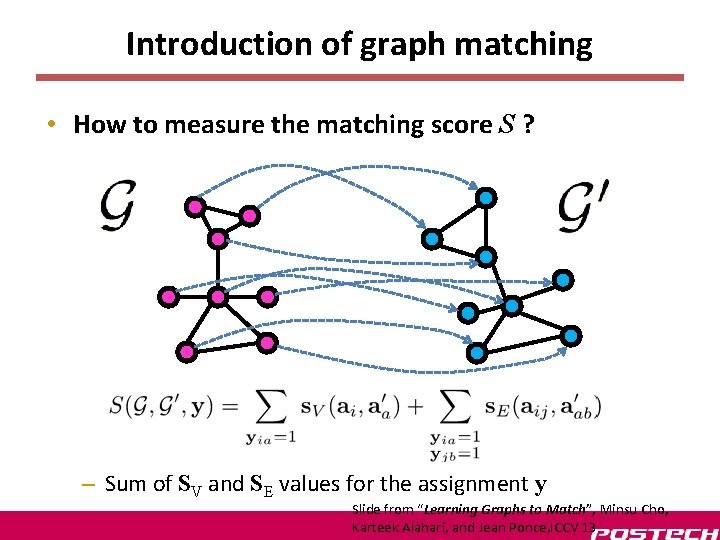
Introduction of graph matching • How to measure the matching score S ? – Each node & each edge has its own attribute – Node similarity function Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

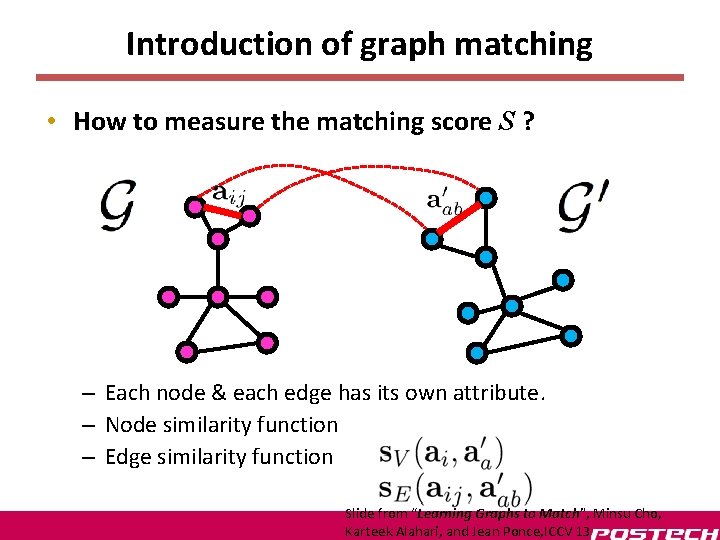
Introduction of graph matching • How to measure the matching score S ? – Each node & each edge has its own attribute. – Node similarity function – Edge similarity function Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

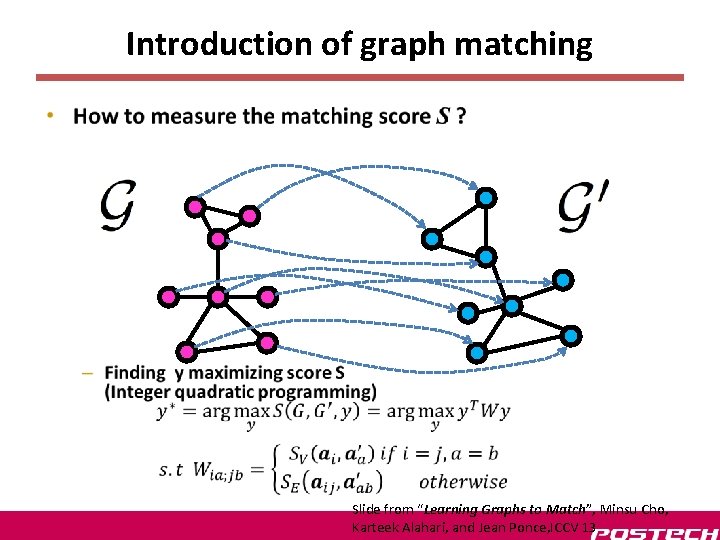
Introduction of graph matching • How to measure the matching score S ? – Sum of SV and SE values for the assignment y Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

Introduction of graph matching • Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

Challenges of graph matching • High time complexity of Integer quadratic programming – NP-hard – Advances in approximate algorithms Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

Paper List • Reweighted Random Walks for Graph Matching - Minsu Cho, Jungmin Lee, and Kyoung Mu Lee, ECCV 10 • Progressive Graph Matching: Making a Move of Graphs via Probabilistic Voting - Minsu Cho and Kyoung Mu Lee, CVPR 12

Reweighted Random Walks for Graph Matching - Minsu Cho, Jungmin Lee, and Kyoung Mu Lee, ECCV 10

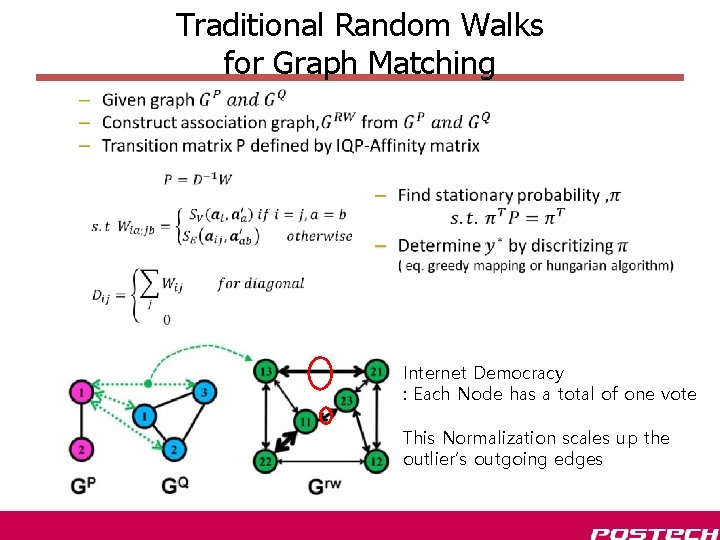
Traditional Random Walks for Graph Matching • Internet Democracy : Each Node has a total of one vote This Normalization scales up the outlier’s outgoing edges

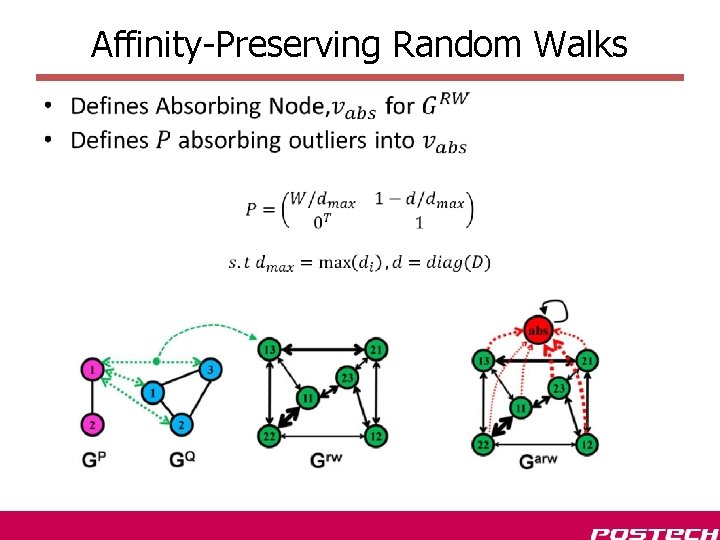
Affinity-Preserving Random Walks •

Affinity-Preserving Random Walks •

Reweighted Random Walks • - Attenuate weak node’s probability - Boost the converging time

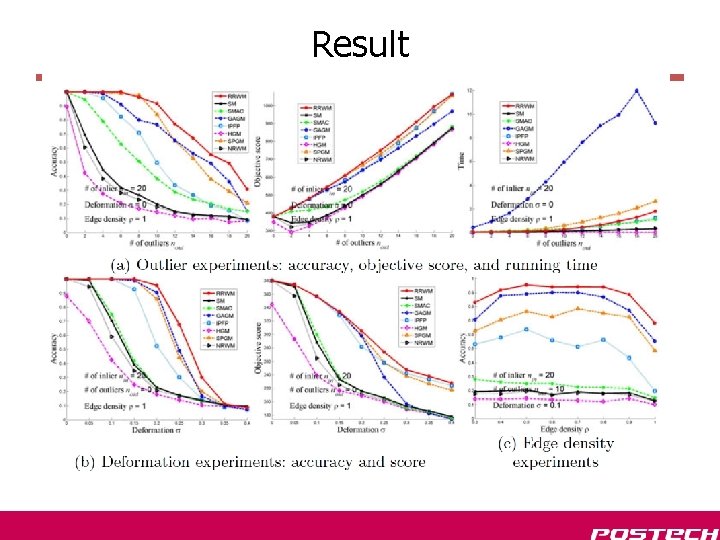
Result

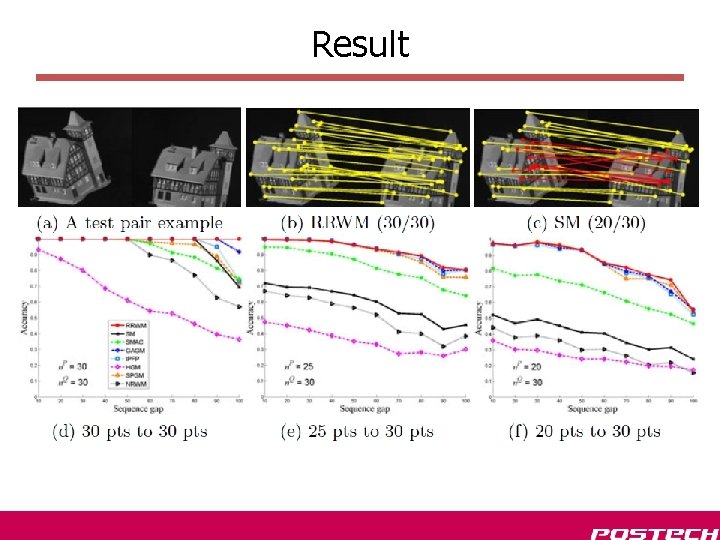
Result

Progressive Graph Matching - Minsu Cho, and Kyoung Mu Lee, CVPR 12

Motivation • Many key points in the images - High time complexity - adverse effect of outliers • Determine sub-graphs active to graph matching : boosting running time • Move the sub-graphs active via probabilistic voting : careful for outliers

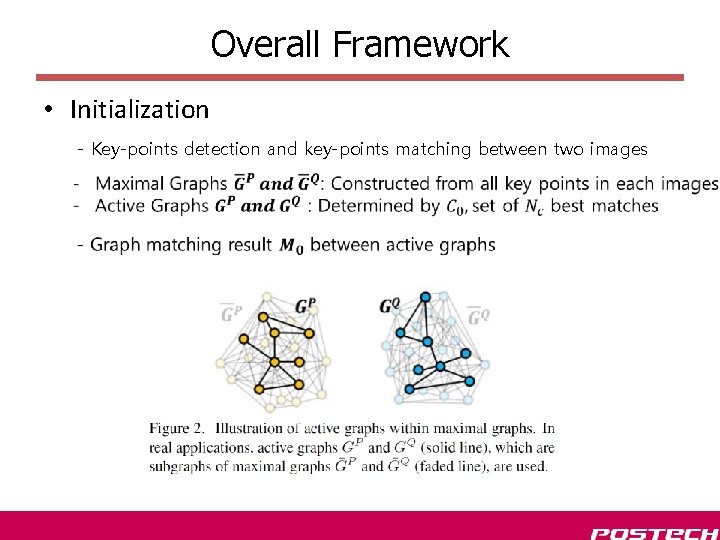
Overall Framework • Initialization - Key-points detection and key-points matching between two images

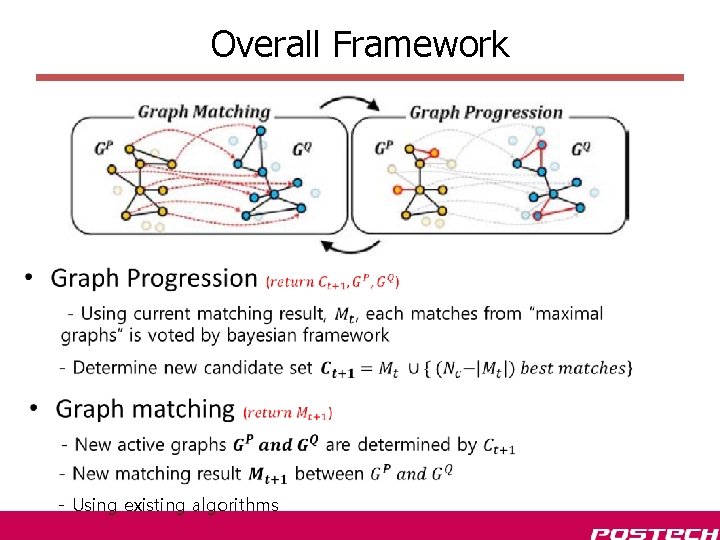
Overall Framework • - Using existing algorithms

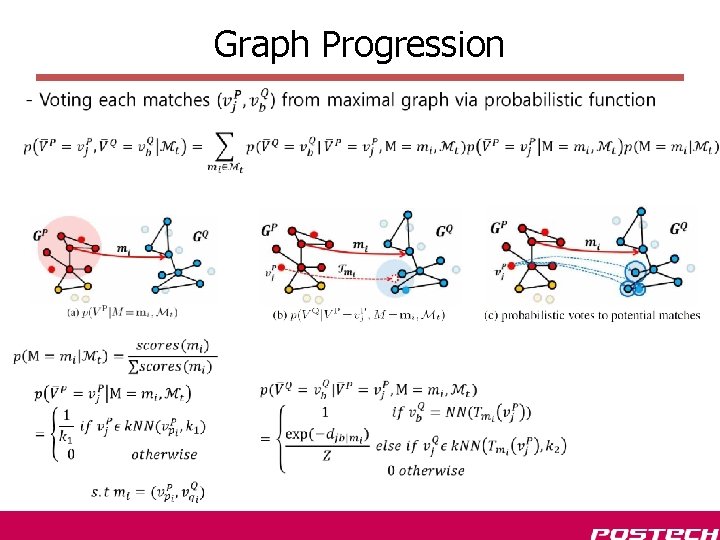
Graph Progression

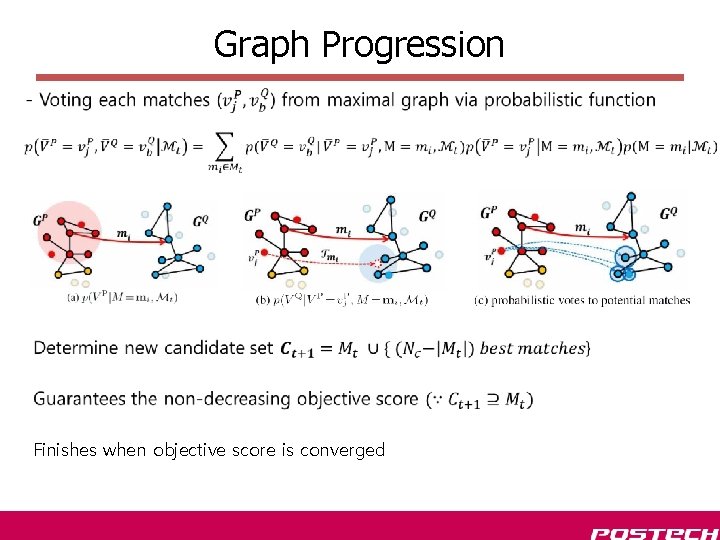
Graph Progression Finishes when objective score is converged

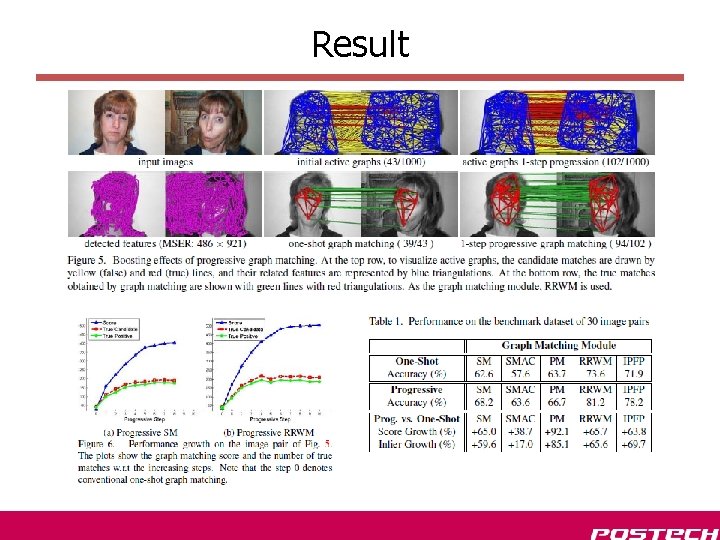
Result

Conclusion • Characteristics of Graph matching - sensitive to outliers • Naïve algorithms • Dependent to definition of attributes