Graph matching algorithms Ilchae Jung Object matching Slide

Graph matching algorithms Ilchae Jung

Object matching Slide from “Linear solution to scale and rotation invariant object matching”, Hao Jiang, Stella X. Yu, CVPR 09

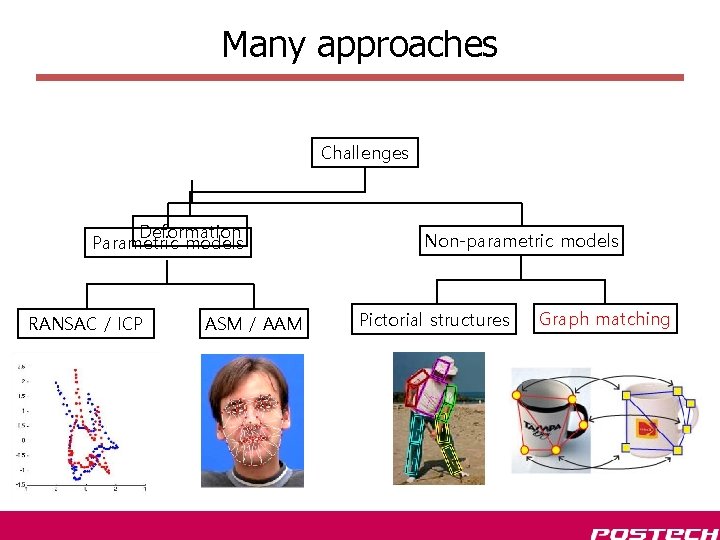
Many approaches Challenges Deformation Parametric models RANSAC / ICP ASM / AAM Non-parametric models Pictorial structures Graph matching

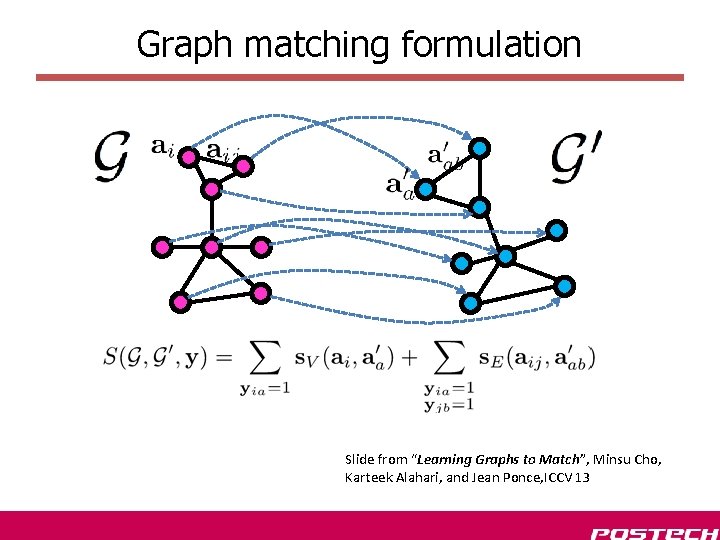
Graph matching formulation Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

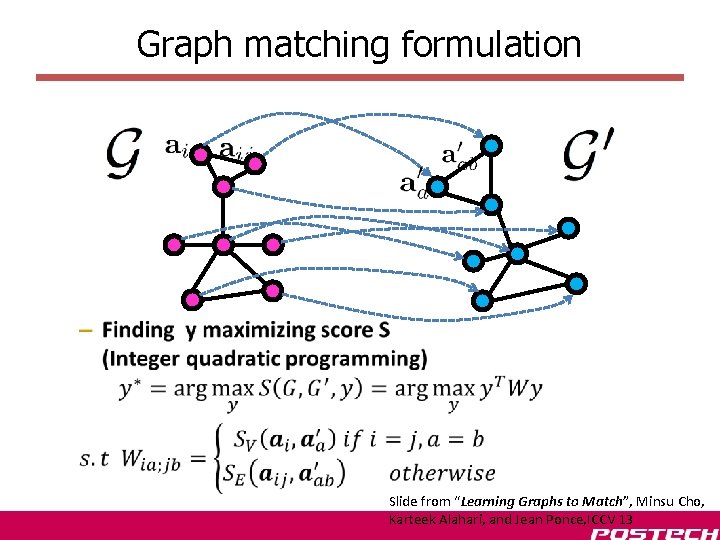
Graph matching formulation • Slide from “Learning Graphs to Match”, Minsu Cho, Karteek Alahari, and Jean Ponce, ICCV 13

Problems • Hardness of application -progressive graph matching • NP-hard problem -relaxed program • Loss of relaxation

papers • Robust feature matching with alternate hough and Inverted Hough Transform (CVPR 2013) - Hsin-Yi Chen, Yen-Yu Lin, Bing-Yu Chen • A Path Following Algorithm for the Graph Matching Problem (PAMI 09) -Mikhail Zaslavskiy, Francis Bach, Jean-Philippe Vert

Robust feature matching with alternate hough and Inverted Hough Transform (CVPR 2013) - Hsin-Yi Chen, Yen-Yu Lin, Bing-Yu Chen

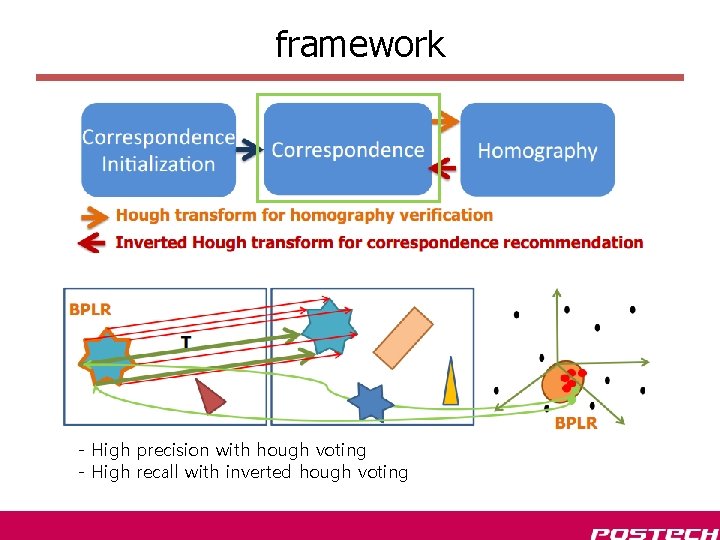
framework - High precision with hough voting - High recall with inverted hough voting

Intialization •

correspondences •

Inverted hough transform •

Whole algorithm

Results

A Path Following Algorithm for the Graph Matching Problem (PAMI 09) -Mikhail Zaslavskiy, Francis Bach, Jean. Philippe Vert

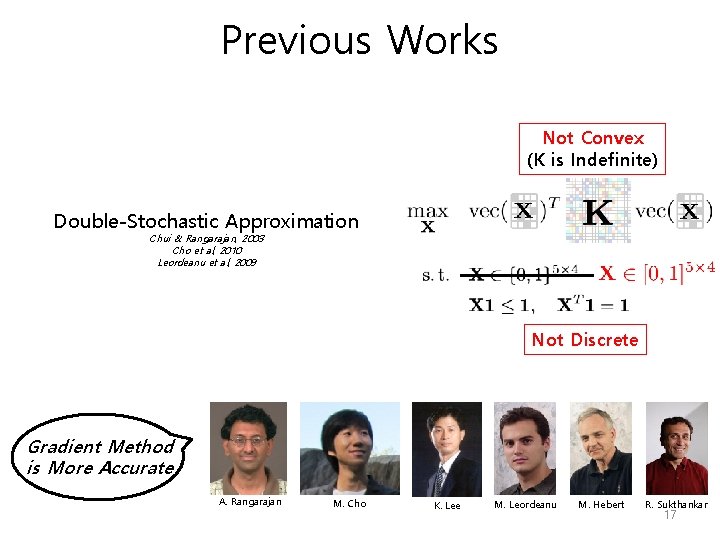
Previous Works Not Convex (K is Indefinite) Double-Stochastic Approximation Chui & Rangarajan, 2003 Cho et al, 2010 Leordeanu et al, 2009 Not Discrete Gradient Method is More Accurate A. Rangarajan M. Cho K. Lee M. Leordeanu M. Hebert R. Sukthankar 17

Hardness of graph matching QAP(quadratic assignment problem) : NP-hard ->Relaxed problem : gradient algorithm with doubly stochastic matrix Not Convex (K is Indefinite) Not Discrete Outperforming rounding algorithm(continous -> discrete) with two equivalent convex/concave relaxation

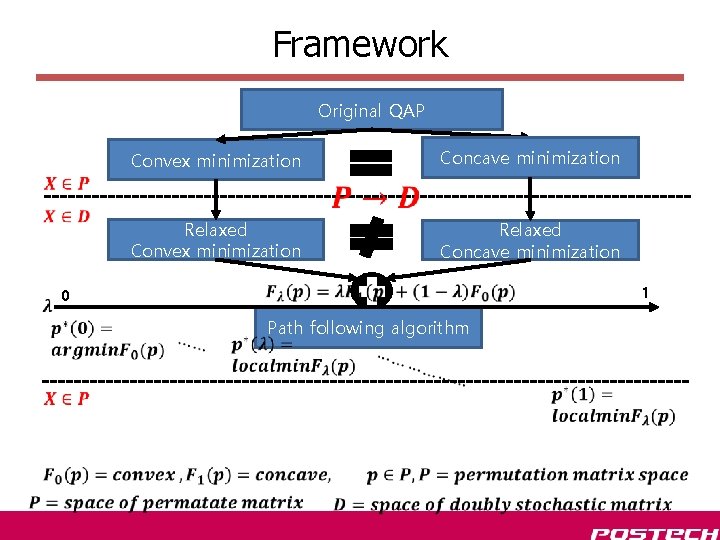
Framework Original QAP Convex minimization Concave minimization Relaxed Convex minimization Relaxed Concave minimization 1 0 Path following algorithm

Example : path following algorithm

Experiment Objective :

Experiment: generated graph 1. Fixing the degree of nodes by Prob. (node degree=k)=VD(k)

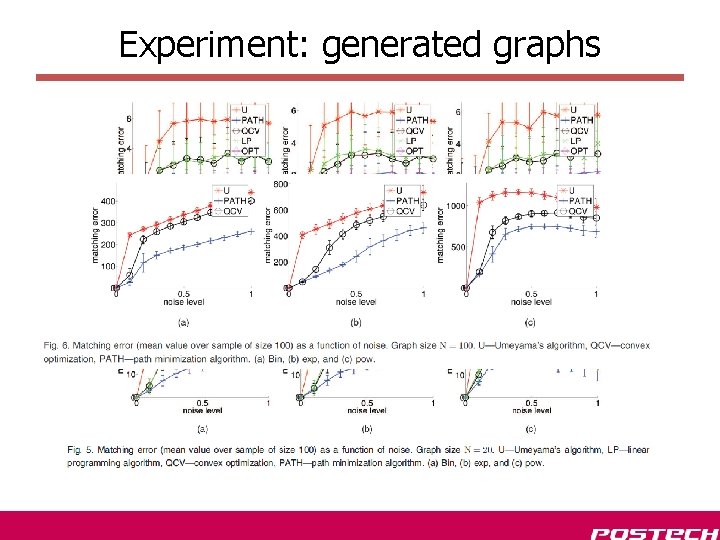
Experiment: generated graphs

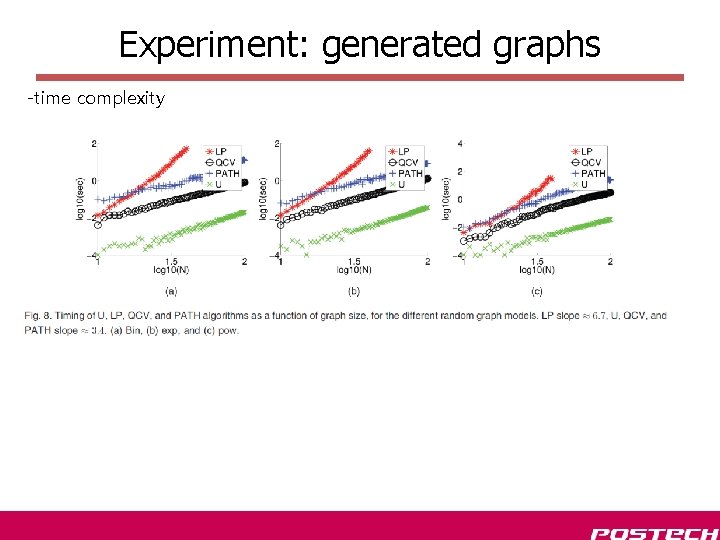
Experiment: generated graphs -time complexity

Discussion • Needs for progressive graph matching • Limitation of relaxation program • High time complexity