Graph in physics education from representation to conceptual

Graph in physics education: from representation to conceptual understanding Marisa Michelini, Alessandra Mossenta, Lorenzo Santi, Alberto Stefanel Research Unit in Physics Education University of Udine, Italy

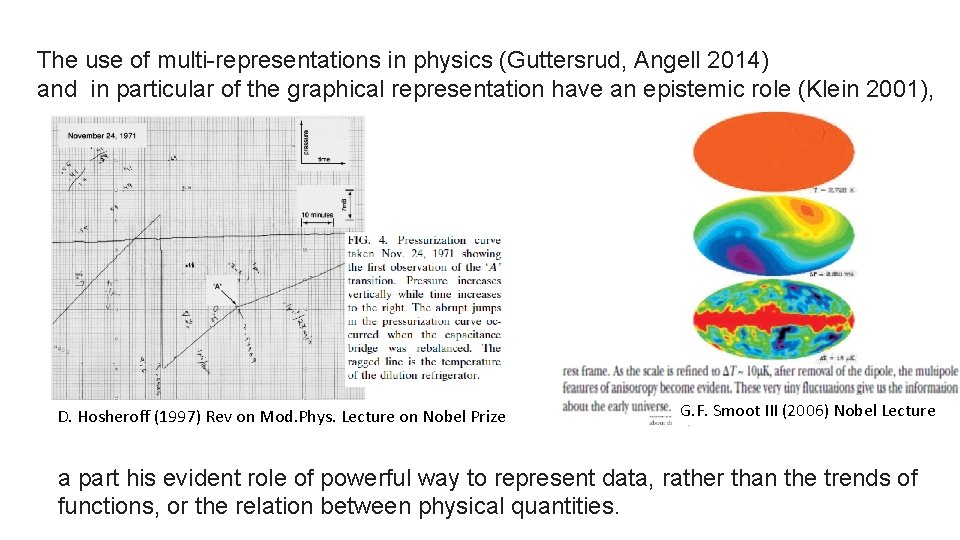
The use of multi-representations in physics (Guttersrud, Angell 2014) and in particular of the graphical representation have an epistemic role (Klein 2001), D. Hosheroff (1997) Rev on Mod. Phys. Lecture on Nobel Prize G. F. Smoot III (2006) Nobel Lecture a part his evident role of powerful way to represent data, rather than the trends of functions, or the relation between physical quantities.

This role has been always stressed in the teaching of physics, but as far as wellknown, with results often ineffective in building students skills such as in reading, interpreting and constructing graphs (Trowbridge, Mc. Dermott 1980, 1981; Beichner 1994; Thornton, Sokoloff 1996; Duit 2009), and in the use of the competencies developed in the purely mathematical field, for such objectives (Beichner 1996). Researches on learning in kinematic stressed that “the ability to relate actual motions and their graphical representations does not automatically develop with acquisition of simple graphing skills, such as plotting points, reading coordinates and finding slopes” (Mc. Dermott 1993)

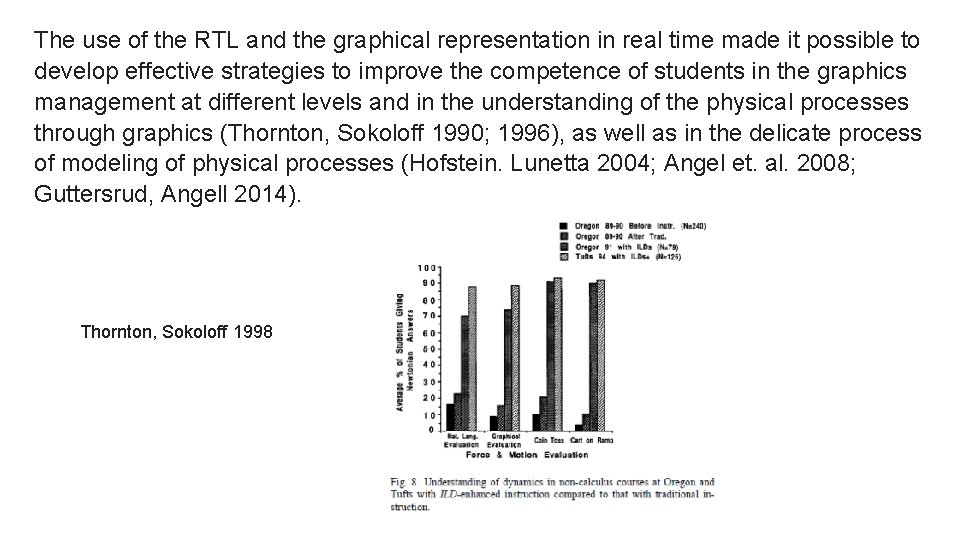
The use of the RTL and the graphical representation in real time made it possible to develop effective strategies to improve the competence of students in the graphics management at different levels and in the understanding of the physical processes through graphics (Thornton, Sokoloff 1990; 1996), as well as in the delicate process of modeling of physical processes (Hofstein. Lunetta 2004; Angel et. al. 2008; Guttersrud, Angell 2014). Thornton, Sokoloff 1998

Many open questions still remain about: - what role can have the graphics in the connection between data and their interpretive meaning - how real-time graphs can act as a bridge in the conceptual construction - and in the building of the laws governing a phenomenon - And finally on how students elaborate a graph acquired with the computer in the experimental laboratory. About these problem areas, this contribution aims to answer four research questions, on which we report examples of research conducted with students of different educational level in the specific topic areas indicated.

RQ. 1. Real-time graphical representation: what conceptual contribution it provides? Case studies are discussed regarding students aged 15 -16 working on motion and forces and students in kindergarten and primary school facing thermal phenomena. RQ. 2. The process of constructing law of the phenomenon: What are the students' representations? What are their difficulties? How do they appropriate of the physical methods? Here we discuss the results of research conducted with students from secondary school in the context of physical optics (Michelini, Santi, Stefanel 2014).

RQ 3. measurement uncertainties on the graphs: what is the significance awareness? Case studies on uncertainty in the analysis of RTL graphs (high school students and college students) RQ 4. Connection of data and their interpretive meaning in a structural model of the matter: what are the reasoning paths of students? It Is presented here a case study of how talent high school students analyzed RBS graphs

Proposals designed according to the MER framework in vertical perspective From phenomenology - to descriptive/phenomenological laws to the interpretative models - to the construction of formal thinking - to the construction of theoretical tought Activity carried out by researchers or teachers prepared by us and monitored using IBL tutorials Analysis according to: - The qualitative research criteria (Erickson F. , 1998; Niedderer 1986; 2010; Denzin N. K. , Lincoln Y. S. , 2011) - Models categorization (Perkins, D. N. , & Grotzer, T. A. 2000; Windschitl, M. A. & Thompson, J. J. 2004) - Representation (Meltzer 2010; Podolefsky, N. S. and N. D. Finkelstein 2006;

Example 1. 1 – Motion graphs N= 74 secondary school students 15 -16 y. o. They know geometry in a cartesian reference 10 h active learning sessions carried out using tutorials and pre/post test Strategy: - presenting the situation - asking for a prevision on graph will be observed in the computer monitor - doing the experiment and report the observed graph - comparing the prevision-experiment graphs - exstrating the analytical forms of the time evolution by the graphs - physical meanings of the parameters Typical sequence: The person walking in front of the sensor The free motion of a car launched on a plane table The motion of the car on an inclined plane ( friction coefficient) The mass-spring oscillator Great increasing in the construction of prevision graphs, in the graphs representation, limited: quantitative, Correct answers in post test

Qualitative behavior (no unit, no values), connection between graphs prevision experiment Comparison: uniform decreasing of v m slope b y intersection (math meanings)

Qualitative behavior (no unit, no values), high attention to the experimental features, connection between graphs prevision experiment Comparison: the experimental curve is not homogeneus [is not smooth] m slope b y intersection (math meanings)

Qualitative behavior (no unit, no values), explicit connection between graphs prevision experiment Comparison: in the experimental graph the part at constant velocity does not appear m (slope) acceleration, negative (physical meaning)

Qualitative behavior (no unit, no values), explicit connection between graphs [but ? ? ] prevision experiment Comparison: «not to much differences. We mantain the correct behavior of precision also in the reality» m slope b y intersection (math meanings) “It is uniform accelerated and it is demonstrated by the comparison between the coefficient of the parabola and the slope of the rectilinear line: if one is double of the other thesis is confirmed. With our curve, we represent correctly the uniform accelerated motion” (Phys meanings)

Example 1. 2 – Temperature graphs Approaching thermal state and processes using on line sensors CLOE LAB ON THERMAL PHENOMENA

The layout of the CLOE Lab on thermal phenomena K 1 – Scenarios: Q: What are the hot/lukewarm/cold objects? A: Let the objects be ordered by groups: hot, lukewarm and cold. O: criteria of order and the way of presentation K 1. 2 - Identify objects which can be considered equally hot: Q 1: The objects which are equally hot, are they all the same? Q 2: There are equal objects that are in different groups? Q 3: There are systems made by equal substance that are in different groups? O: thermal state related to the state and not to the material K 1. 3 – How do you can establish that a system is hot/cold? O 1. “with our hand”, “by touching it”, “by looking O 2: “with a thermometer, others again said at” the object and relying on one’s own experience K 2 – Exploration of thermal properties of system using senses: Objects on the table. K 3 – Exploration of thermal states & processes, with sensors as extension of senses

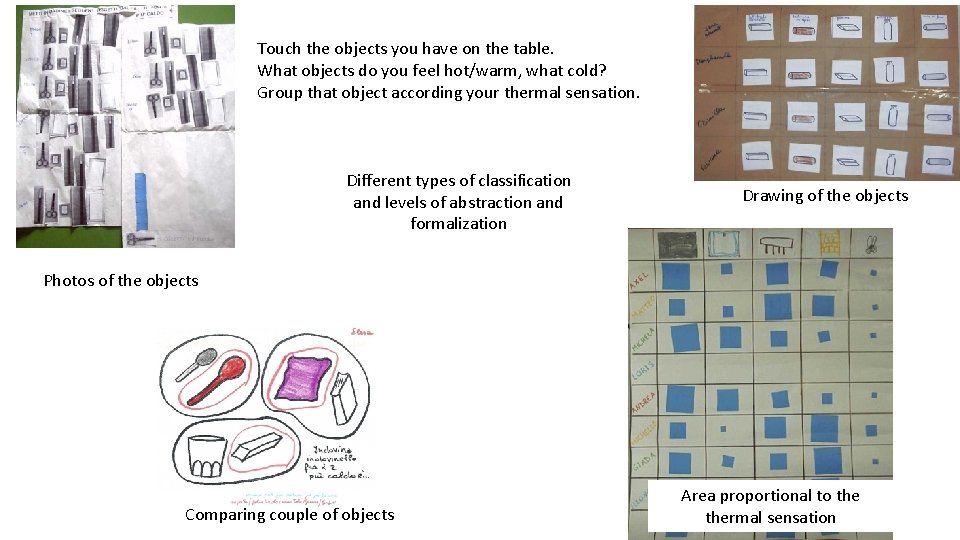
Touch the objects you have on the table. What objects do you feel hot/warm, what cold? Group that object according your thermal sensation. Different types of classification and levels of abstraction and formalization Drawing of the objects Photos of the objects Comparing couple of objects Area proportional to thermal sensation

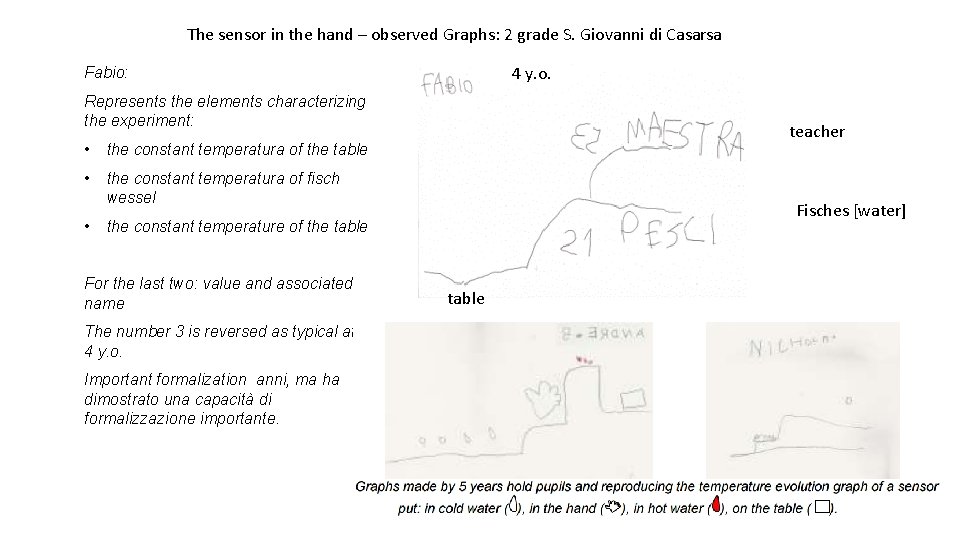
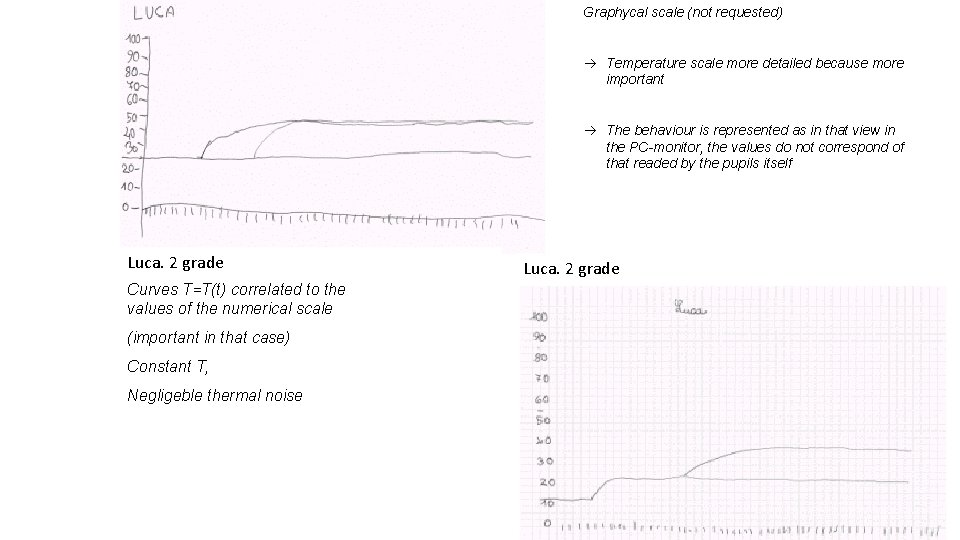
The sensor in the hand – observed Graphs: 2 grade S. Giovanni di Casarsa 4 y. o. Fabio: Represents the elements characterizing the experiment: • the constant temperatura of the table • the constant temperatura of fisch wessel • teacher Fisches [water] the constant temperature of the table For the last two: value and associated name The number 3 is reversed as typical at 34 y. o. Important formalization anni, ma ha dimostrato una capacità di formalizzazione importante. table

Graphycal scale (not requested) Temperature scale more detailed because more important The behaviour is represented as in that view in the PC-monitor, the values do not correspond of that readed by the pupils itself Luca. 2 grade Curves T=T(t) correlated to the values of the numerical scale (important in that case) Constant T, Negligeble thermal noise Luca. 2 grade

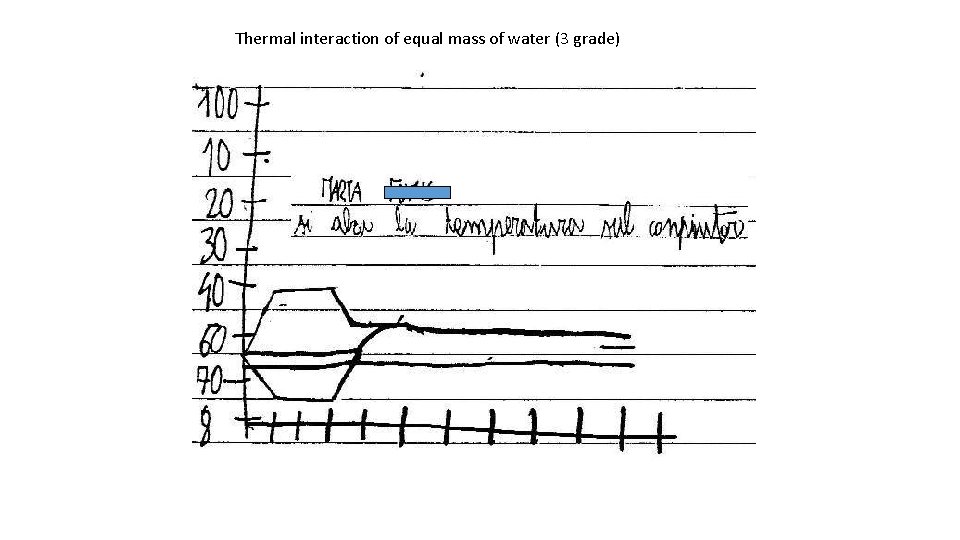
Thermal interaction of equal mass of water (3 grade)

The cursor proved to be decisive: identify quantitative aspects; associate phenomena and data. Identifying critical instant in the evolution of the temperature: from 15%, becomes mastered by 95% (rarely: differences in temperature and time intervals) Analyzing the graph, 60% of the children can predict the final thermal state of a process. 20%: by looking at the way the temperature varies in time (intuitive derivative idea) 72% of the children tends to objectualize the graph (48%) or the temperature (24%) (“the red sensor increases”, “the temperature goes away straight”)(observed also with adults) 78% processes from the graph thermal equilibrium temperature 22 % connect graph representation and numerical data displays …. The cursor helps 66% of the children to overcome the missing connection between numerical values and the graph.

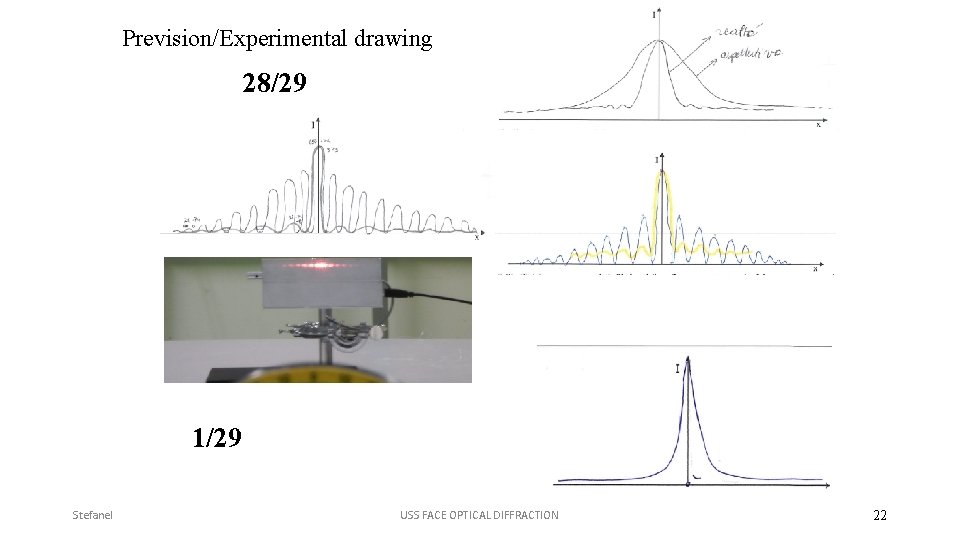
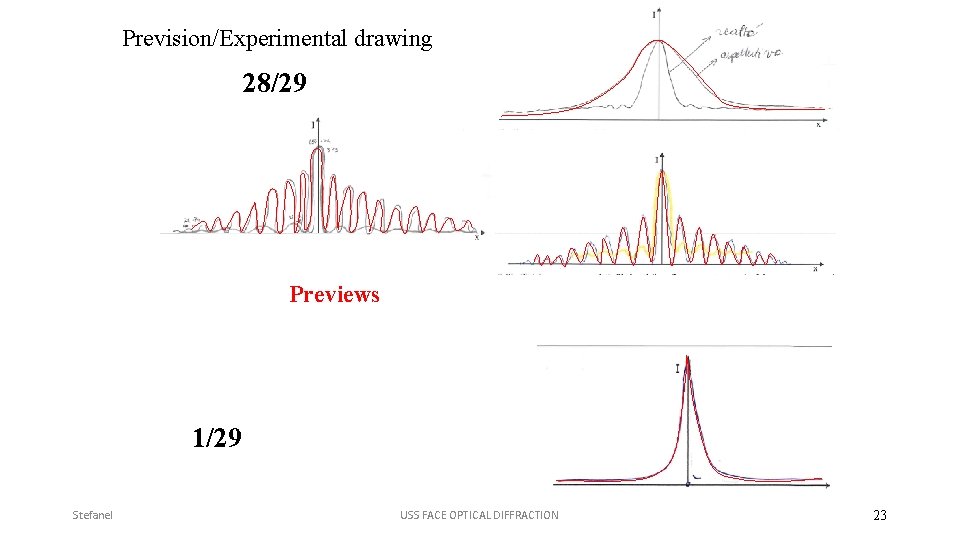
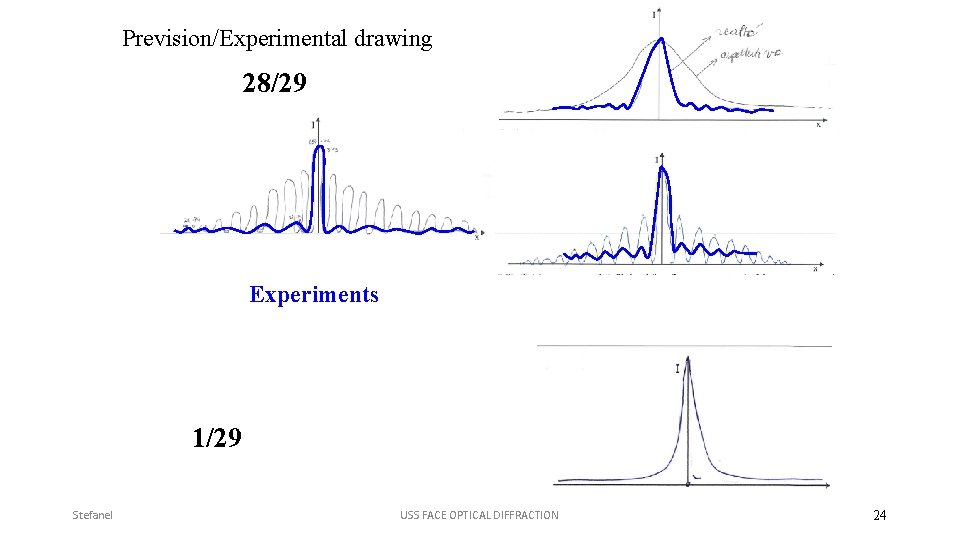
Example 2. 1. – Diffraction graphs 1 h pre-test (by care of school teacher) 4 h: activity carried out by a researcher - qualitative and quantitative exploration of the light diffraction (a laser beam diffracted by a single slit 5 mm 0. 24 mm) using tutorials 1 h test out (by care of school teacher) N= 29 students 17/18 y. o. – Scientific Lyceum (Tarvisio) This students know to study a function using derivative; usually they are involved in the analysis of complicated function like this: x y = ------ 1 -x

Prevision/Experimental drawing 28/29 1/29 Stefanel USS FACE OPTICAL DIFFRACTION 22

Prevision/Experimental drawing 28/29 Previews 1/29 Stefanel USS FACE OPTICAL DIFFRACTION 23

Prevision/Experimental drawing 28/29 Experiments 1/29 Stefanel USS FACE OPTICAL DIFFRACTION 24

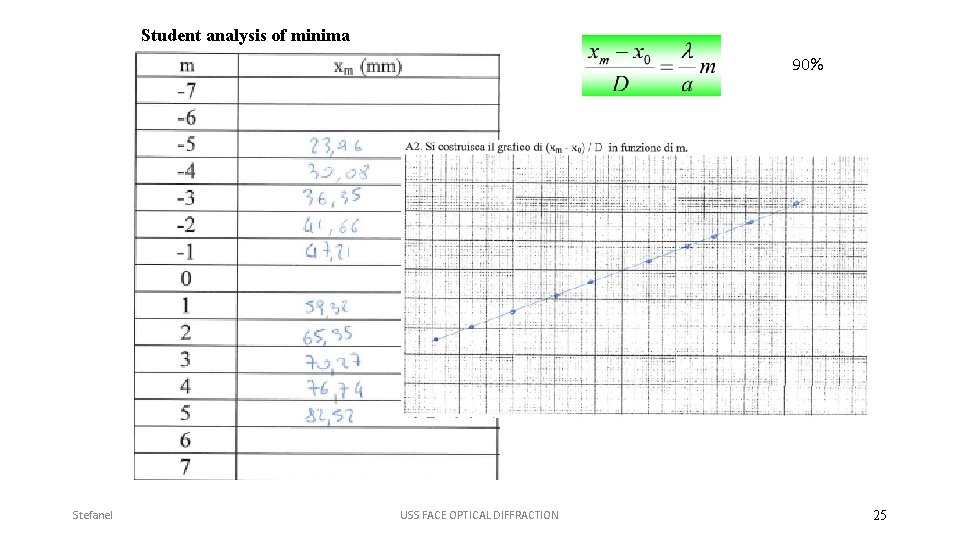
Student analysis of minima 90% Stefanel USS FACE OPTICAL DIFFRACTION 25

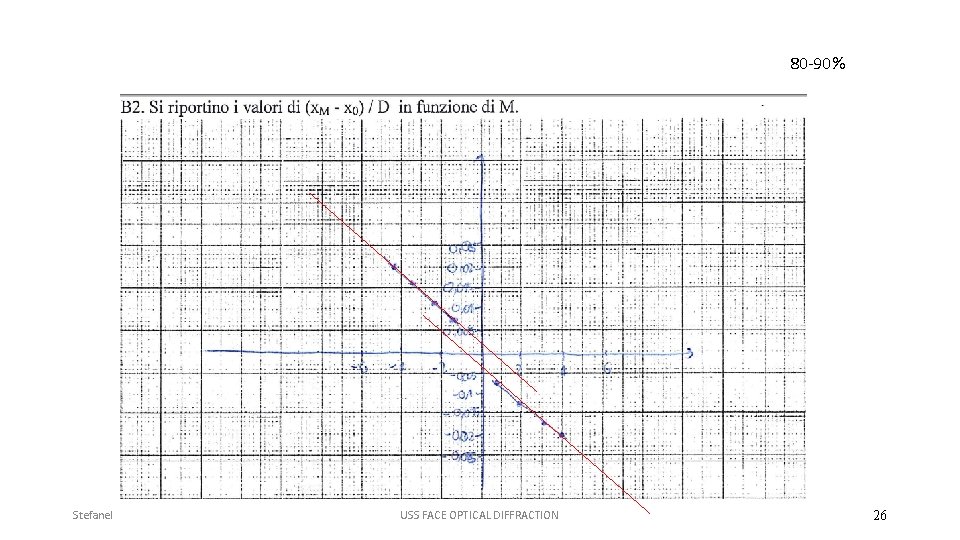
80 -90% Stefanel USS FACE OPTICAL DIFFRACTION 26

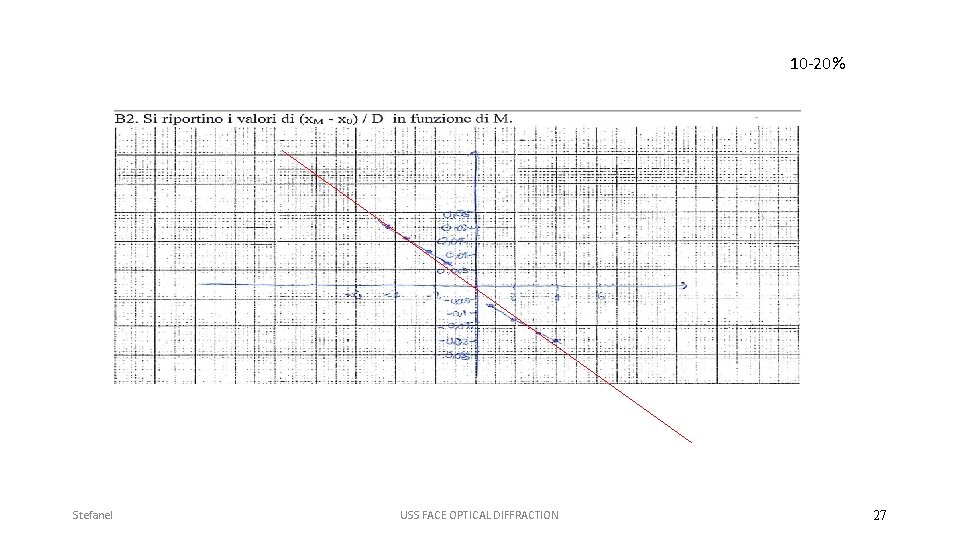
10 -20% Stefanel USS FACE OPTICAL DIFFRACTION 27

60% Stefanel USS FACE OPTICAL DIFFRACTION 28

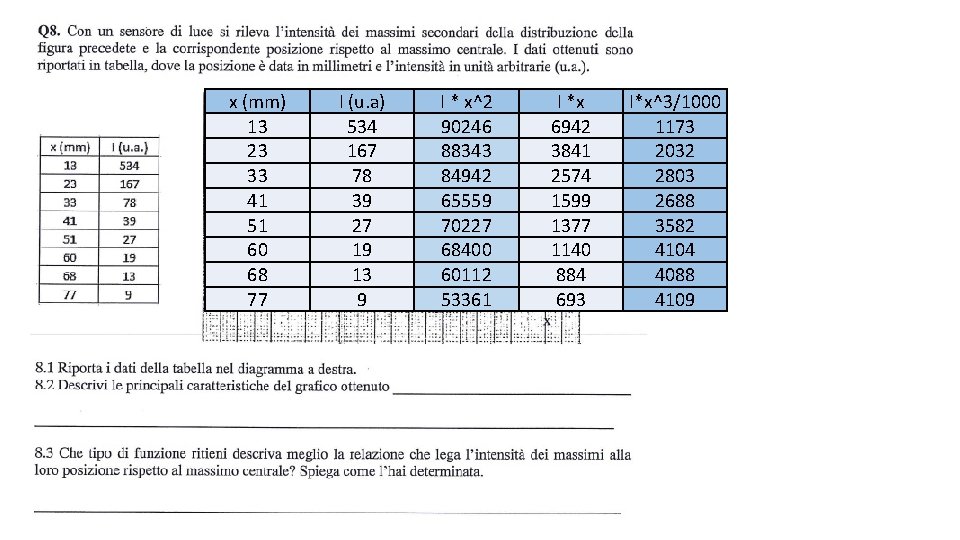
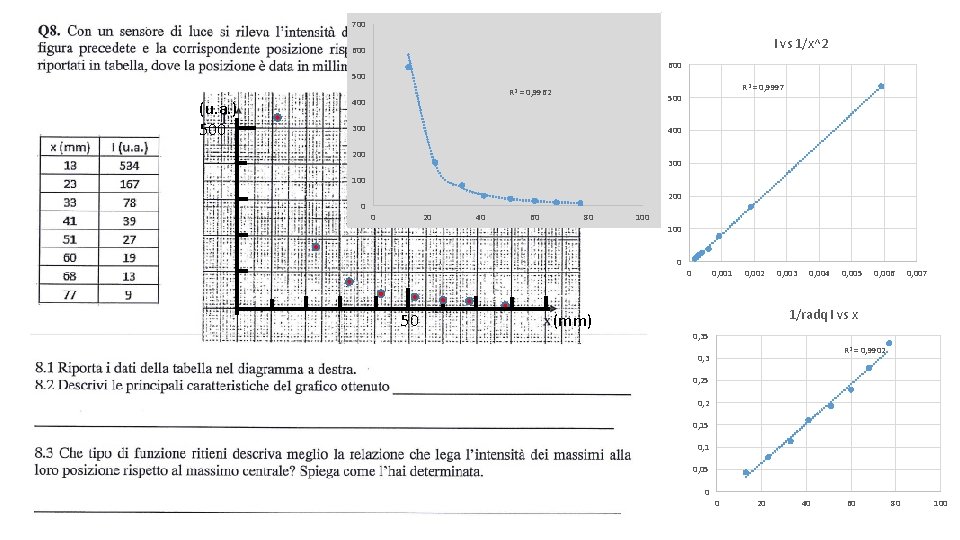
An on-line light sensor measure the intensity of the maxima and the position with respect to the central maximum of the distribution reported in the figure The data are reported in the table • Report the data in the diagram • Describe the principal characteristic of the graph obtained • Which kind of function describe better the relation between the maxima intensity vs their position? Explain how you determine it.

x (mm) 13 23 33 41 51 60 68 77 I (u. a) 534 167 78 39 27 19 13 9 I * x^2 90246 88343 84942 65559 70227 68400 60112 53361 I *x 6942 3841 2574 1599 1377 1140 884 693 I*x^3/1000 1173 2032 2803 2688 3582 4104 4088 4109

700 I vs 1/x^2 600 500 (u. a. ) 500 R 2 = 0, 9962 400 R 2 = 0, 9997 500 300 400 200 300 100 0 20 40 60 80 100 0 50 (mm) 0 0, 001 0, 002 0, 003 0, 004 0, 005 0, 006 0, 007 1/radq I vs x 0, 35 R 2 = 0, 9902 0, 3 0, 25 0, 2 0, 15 0, 1 0, 05 0 0 20 40 60 80 100

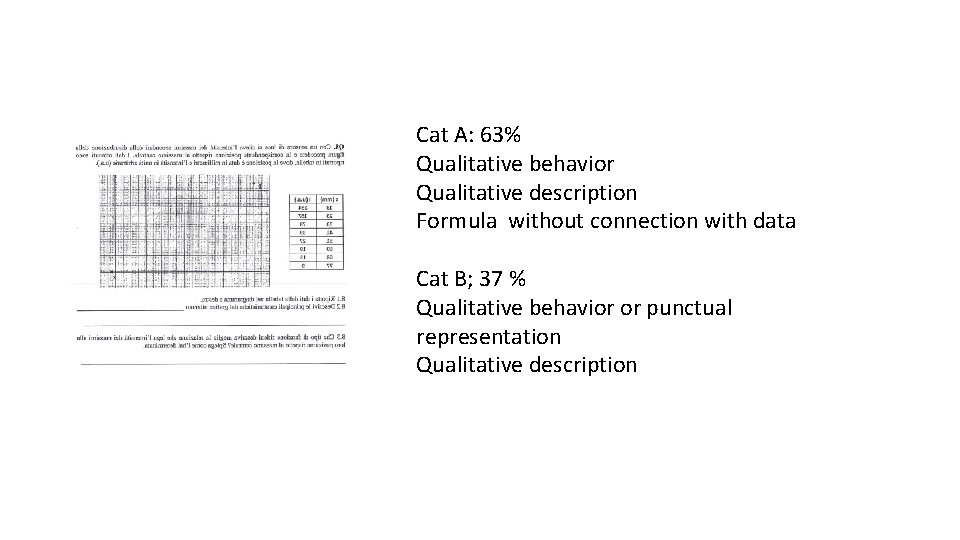
Cat A: 63% Qualitative behavior Qualitative description Formula without connection with data Cat B; 37 % Qualitative behavior or punctual representation Qualitative description

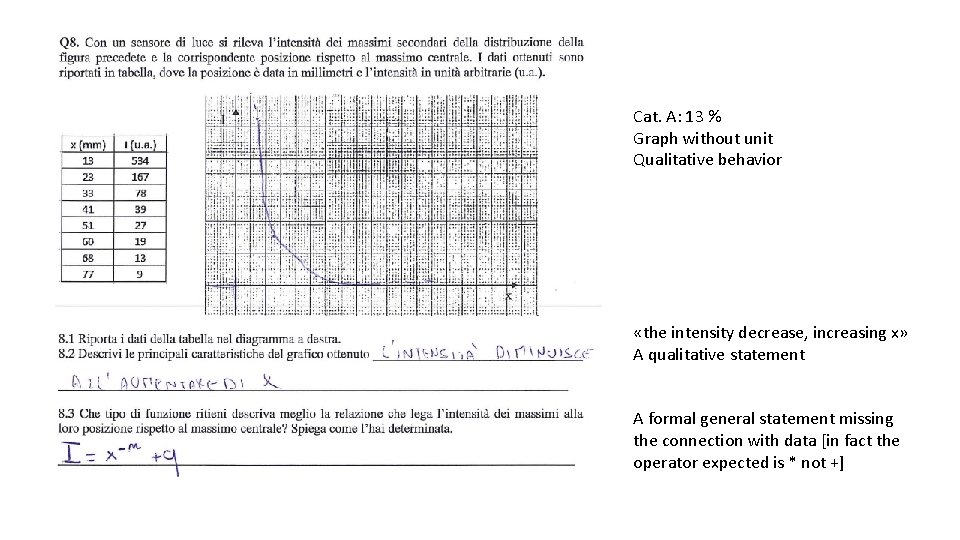
Cat. A: 13 % Graph without unit Qualitative behavior «the intensity decrease, increasing x» A qualitative statement A formal general statement missing the connection with data [in fact the operator expected is * not +]

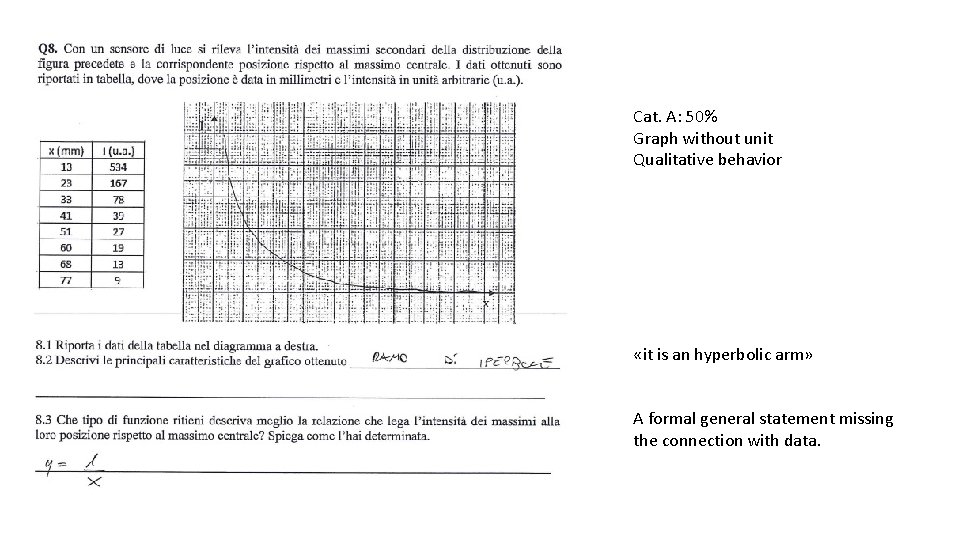
Cat. A: 50% Graph without unit Qualitative behavior «it is an hyperbolic arm» A formal general statement missing the connection with data.

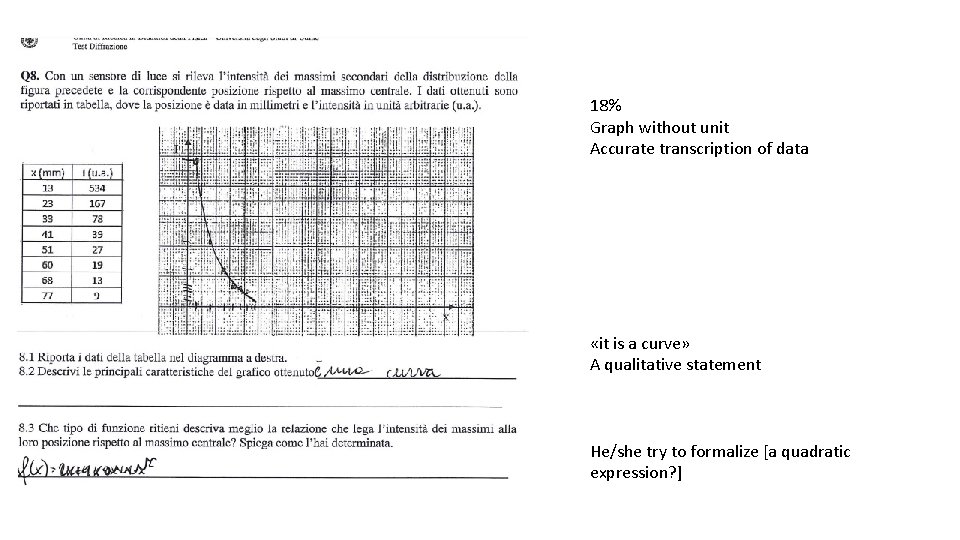
18% Graph without unit Accurate transcription of data «it is a curve» A qualitative statement He/she try to formalize [a quadratic expression? ]

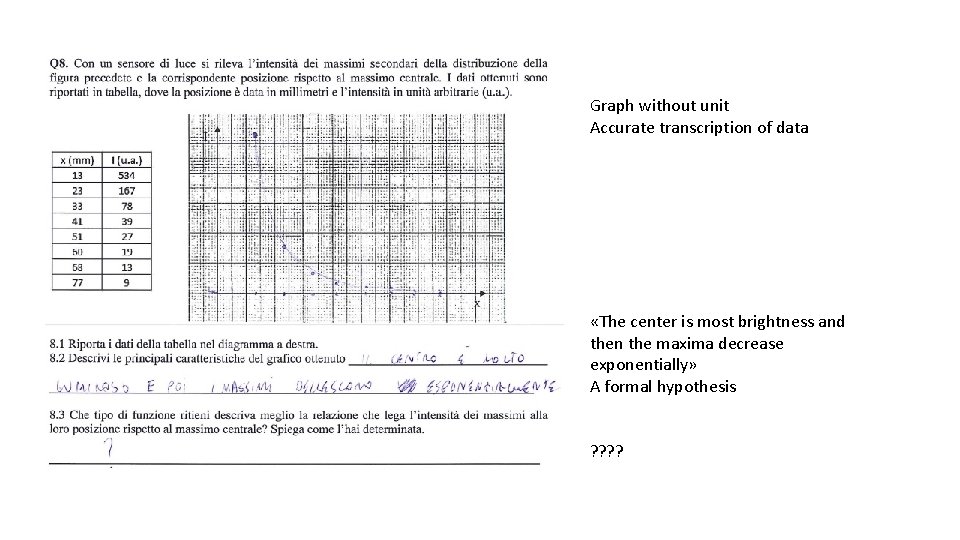
Graph without unit Accurate transcription of data «The center is most brightness and then the maxima decrease exponentially» A formal hypothesis ? ?

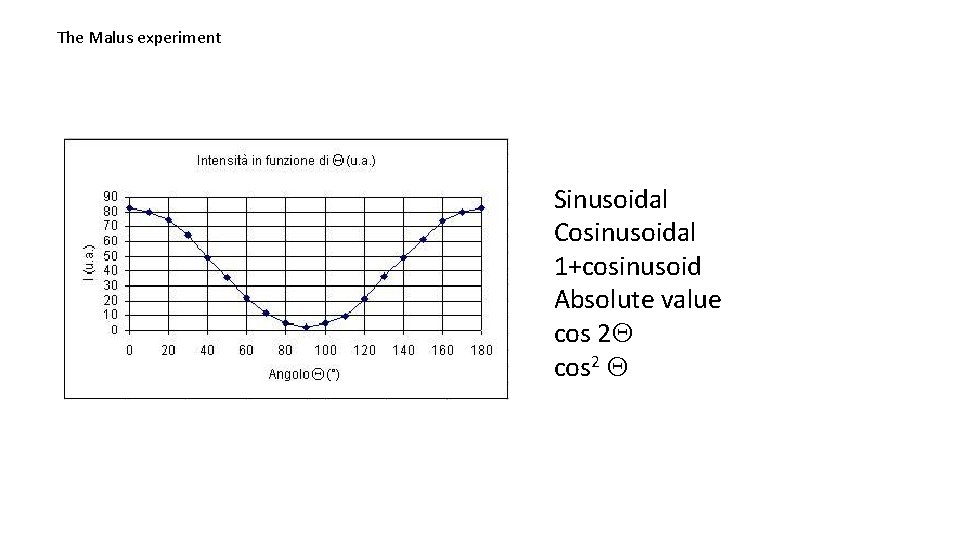
The Malus experiment Sinusoidal Cosinusoidal 1+cosinusoid Absolute value cos 2

Conclusion RQ. 1. Real-time graphical representation: what conceptual contribution it provides? Case studies are discussed regarding students aged 15 -16 working on motion and forces and students in kindergarten and primary school facing thermal phenomena. These shows the role that the graph has in: - linking the phenomenon to its description by physical quantities - in linking the physical processes underlying these phenomena and characteristics of the iconic graphics - in building formal thought - as well as developing skills in mathematical formalization (Michelini et al 2010; Michelini 2010).

Conclusion RQ. 2. The process of constructing law of the phenomenon: What are the students' representations? What are their difficulties? How do they appropriate of the physical methods? Here we discuss the results of research conducted with students from secondary school in the context of physical optics (Michelini, Santi, Stefanel 2014). On one hand it documents how students analyze and manage data related to a distribution of light intensity diffracted by single slit to build the laws that describes the phenomenon and the difficulties of some students in going beyond the use of the only direct proportionality. On the other we will discuss how students construct an analytical description of the results of the experiment of Malus as a transition to the interpretive level (both at the classical level, both quantum).

Conclusion RQ 3. measurement uncertainties on the graphs: what is the significance awareness? About this aspect are discussed case studies related to high school students and college students in the discussion of the uncertainty of measurement related to the analysis of graphs collected with computer, which shows a general tendency to overlook the role of 'measurement uncertainty and thus to be fully aware of the significance of physical build relationships (Michelini, Santi, Stefanel 2014).

Conclusion RQ 4. Connection of data and their interpretive meaning in a structural model of the matter: what are the reasoning paths of students? It Is presented here a case study of how talent high school students analyzed RBS graphs, in particular documenting what is the interpretative contribution and role of graphics transduction into energy to provide information on the impact location and composition of the sample (Mossenta 2010; Michelini, Sainti, Stefanel 2014).