Graph Cut Algorithms for Computer Vision Medical Imaging

Graph Cut Algorithms for Computer Vision & Medical Imaging Ramin Zabih Computer Science & Radiology Cornell University Joint work with Y. Boykov, V. Kolmogorov, A. Raj and O. Veksler

Outline n Pixel labeling problems n n Graph cuts n n Expansion move algorithm Beyond regularity n n Piecewise constant property of the image Reconstructing MRI’s via graph cuts LBP versus graph cuts

Pixel labeling problem Given Find Labeling f = (f 1, …, fn) 2 5 1 3 4 Assignment cost for giving a particular label to a particular node. Written as D. Separation cost for assigning a particular pair of labels to neighboring nodes. Written as V. 3 4 Such that the sum of the assignment costs and separation costs (the energy E) is small

Solving pixel labeling problems n n n We want to minimize the energy E(f) Classical problem in vision and beyond Bayesian justification n Markov Random Fields (MRF’s)

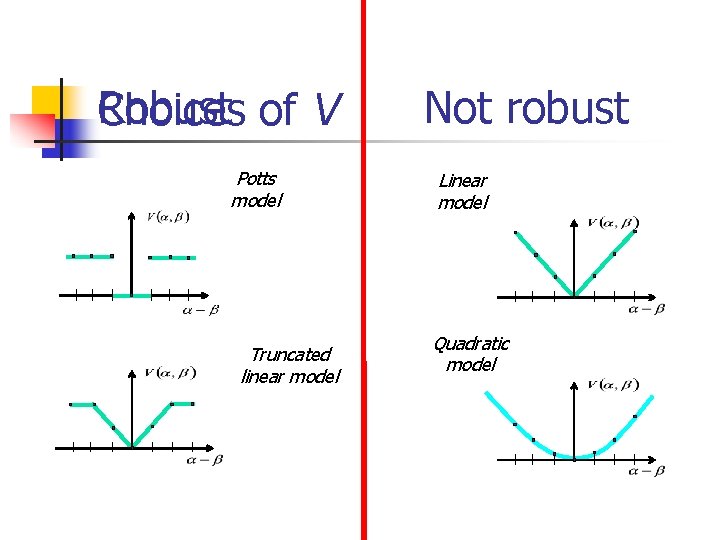
Robust Choices of V Potts model Truncated linear model Not robust Linear model Quadratic model

Pixel labeling for stereo Stereo n n n Labels are shifts (hence depths) Assignment cost from intensity difference Neighboring pixels should be at similar depths n Except at the borders of objects!

How to minimize the energy? n Until late-90’s, poor solutions n n In vision, we tend to focus on the deriving the “right” energy function n n Problem is NP-hard [K/BVZ PAMI ’ 01] Minimize via general-purpose methods Computer scientists disagree n n General-purpose methods must be weak Nearby energy functions can be “easy”

Sample results Right answers Graph cuts Correlation Dynamic programming

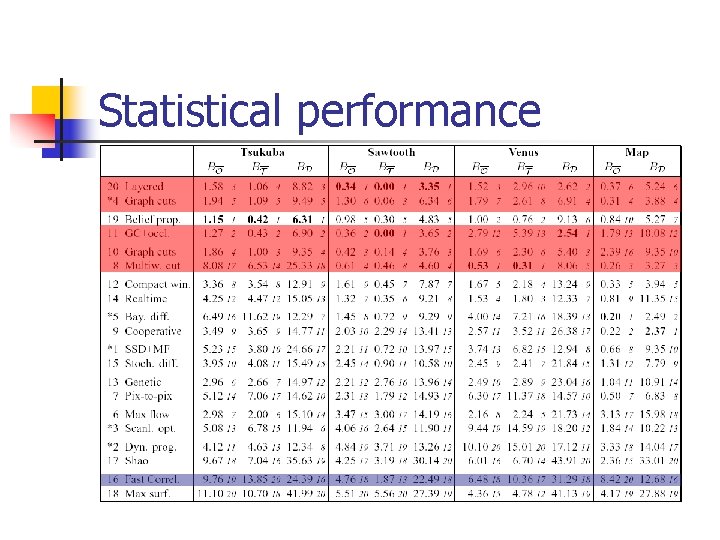
Statistical performance

Graph cuts and expansion moves

Graph cuts n Reduce energy minimization problem to computing the min s-t cut on a graph n n n Cuts are labelings, cut costs are energy Rapidly solvable by max flow Running times are linear in the number of pixels and labels n Asymptotically, low-order polynomial

What do graph cuts provide? n n For less interesting V, polynomial algorithm for global minimum! For a particularly interesting. V, approximation algorithm n n n Proof of NP hardness For many choices of V, algorithms that find a “strong” local minimum Very strong experimental results

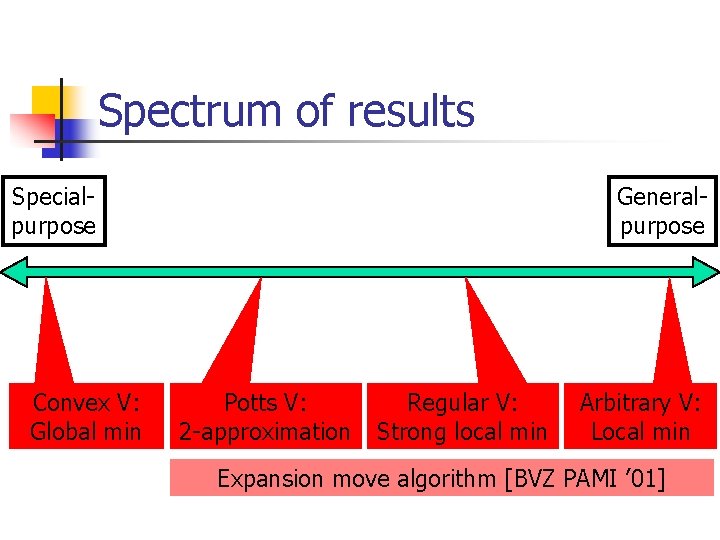
Spectrum of results Specialpurpose Convex V: Global min Generalpurpose Potts V: 2 -approximation Regular V: Strong local min Arbitrary V: Local min Expansion move algorithm [BVZ PAMI ’ 01]

Gradient descent methods n Subproblem: pick a pixel, find the label that minimizes E, repeat n n Minimize restricted version of E Computes a local minimum (line search)

Gradient descent vs. Graph cuts n Continuous vs. discrete n n n Local min in line search vs. global min Minimize over a line vs. hypersurface n n No floating point with graph cuts Containing O(2 n) candidates Local minimum: weak vs. strong n n 2 -approximation for the Potts model Within much less than 1% of global min!

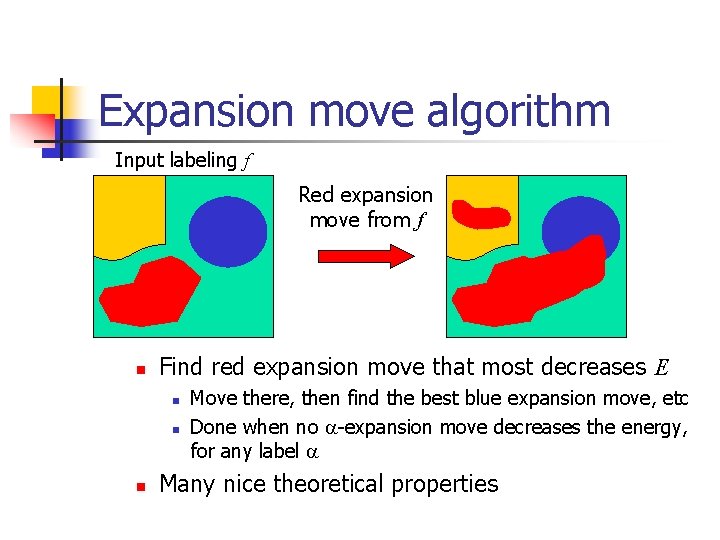
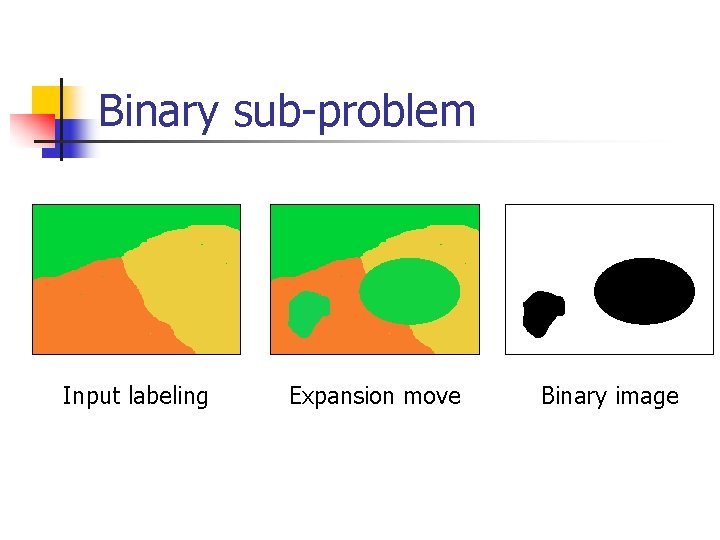
Expansion move algorithm Input labeling f Red expansion move from f n Find red expansion move that most decreases E n n n Move there, then find the best blue expansion move, etc Done when no -expansion move decreases the energy, for any label Many nice theoretical properties

2 -approximation for Potts model optimal solution local minimum Summing up over all labels:

Expansion moves in action initial solution -expansion -expansion For each move we choose expansion that gives the largest decrease in the energy: binary energy minimization subproblem

Binary sub-problem Input labeling Expansion move Binary image

Expansion move energy Goal: find the binary image with lowest energy Binary image energy is a restriction of E Depends on f,

Graph cuts solution n n This can be done as long as V has a specific form (works for arbitrary D) Regularity constraint [KZ PAMI ’ 04] n Can find cheapest -expansion from f if

Regular choices of V n Suppose that V is a metric n Then what?

Applications in vision n n Two tricks to get best stereo answers Monocular cues (“fragile constraint”) combine segmentation and stereo n n Without understanding image statistics Continuous label sets exploit the power of the Potts model n Labels can be planes or smooth surfaces

Applications outside vision n Kleinberg & Tardos [FOCS ’ 98][JACM ’ 02] gave an approximation algorithm when V is a metric n n Recent applications in SIGGRAPH n n Various follow-up papers 1 paper in ’ 03, >5 papers (!) in ’ 04 Key limitation: regularity

Beyond regularity What energy functions can’t be minimized via graph cuts?

Beyond regularity n n Arbitrary non-regular functions are NPhard Only regular functions can be solved via graph cuts n n I. e. , compute optimal expansion move Very recent work has relaxed this restriction n n Kolmogorov & coworkers (Digital Tapestry) Raj & Zabih

Other energy functions? n You can make a non-regular function regular n n n Can find optimal expansion move for new energy What does this say about the original energy? If you do this correctly, the original energy never increases! n n Digital tapestry: careful truncation for arbitrary V Raj & Zabih: linear inverse problems

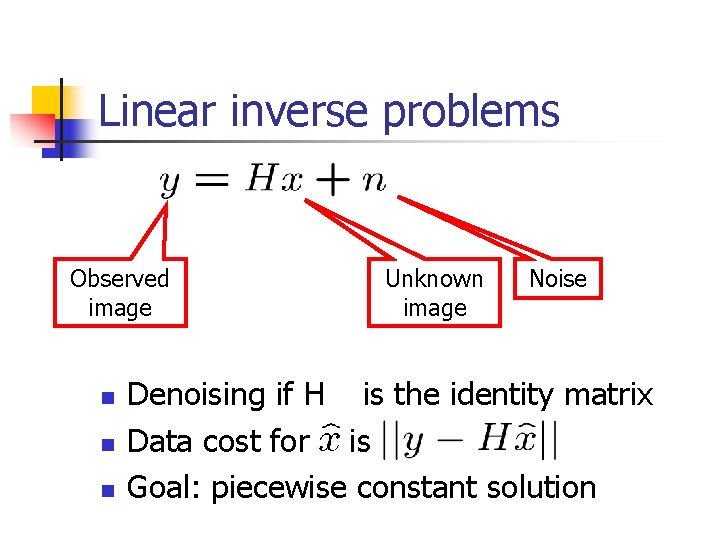
Linear inverse problems Observed image n n n Unknown image Noise Denoising if H is the identity matrix Data cost for is Goal: piecewise constant solution

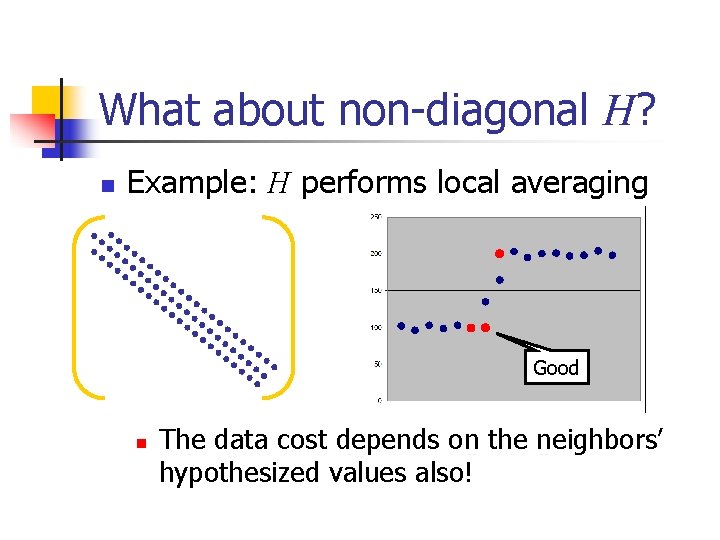
What about non-diagonal H? n Example: H performs local averaging Good n The data cost depends on the neighbors’ hypothesized values also!

Regularity is a challenge n n For non-negative H, the energy function is regular iff Can compute the optimal -expansion move for a pixel below where all its neighbors are above (or vice-versa) n This is true for very few pixels!

Strategy n At a given point we are given f, n The energy function will depend on them n n Dynamically updated as the algorithm runs E’(f, ) is a regular approximation to the non-regular E we want to minimize n Can find -expansion that most reduces E’

Approximation n n For each , split pixel pairs into those with regular cost vs non-regular cost: Approximate E 2 terms using input labeling f :

Approximation properties n n Additional approximations are also made to increase the number of pixels that can move to Reducing the modified energy is guaranteed to reduce the original energy n Modified energy is very close to the original when few pixels move to

Reconstructing MRI’s via Graph Cuts (or: MRF’s for MRI’s)

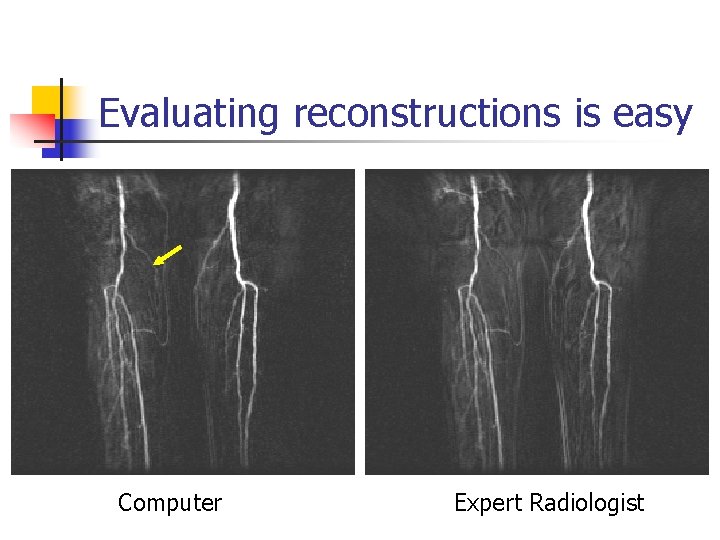
Reconstructing MRI’s n MR requires substantial cleverness in image formation n Unique among image modalities Under-appreciated task of Radiologists Acquisition speed really matters n Physiological processes take place at different timescales n Heartbeat, respiration, etc.

Evaluating reconstructions is easy Computer Expert Radiologist

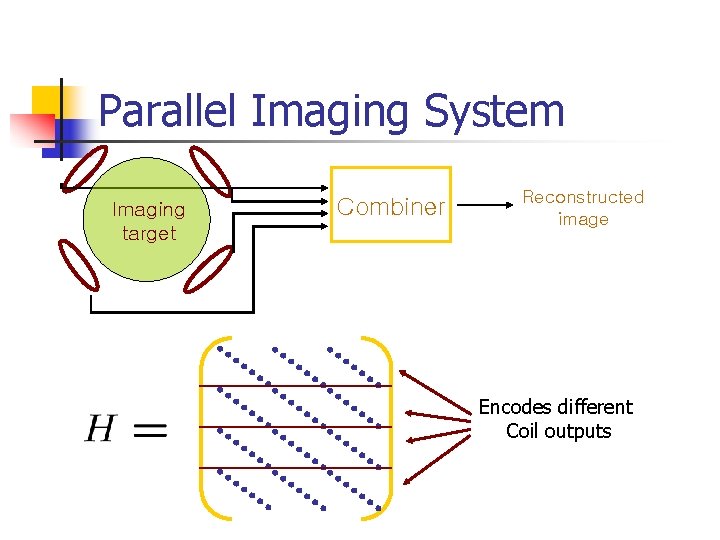
Parallel Imaging System Imaging target Combiner Reconstructed image Encodes different Coil outputs

Graph cut reconstruction n Reconstruct the image to be consistent with the observed data n n n Standard reconstruction algorithm (SENSE) uses least squares n n Each coil gives aliased data Coils have different spatial sensitivities Equivalent to maximum likelihood Graph cuts can impose smoothness

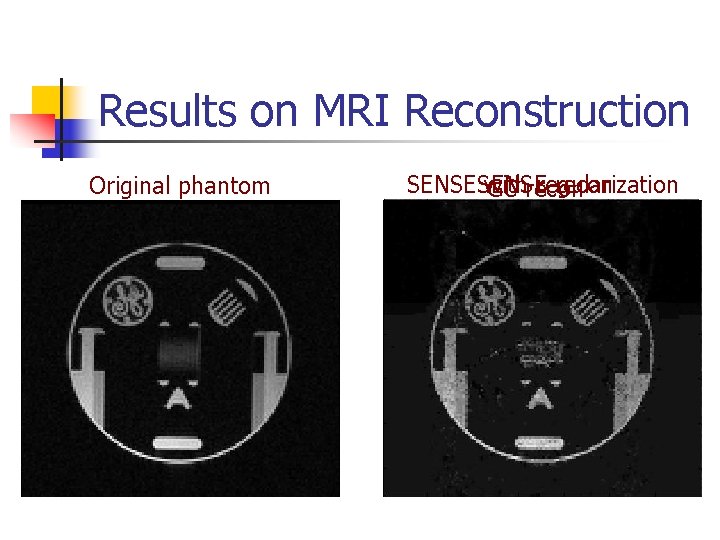
Results on MRI Reconstruction Original phantom recon SENSE with regularization GC recon

Zoomed results Original phantom SENSE with GC recon regularization recon

Conclusions n Powerful optimization tool for vision n And beyond… Trade off generality versus power More general than thought n Even applicable to medical imaging

Graph cuts versus LBP n Evaluation criteria: n n Application effectiveness: comparable n n Probably the most important criterion Speed: LBP is now faster for stereo n n Application effectiveness, speed, quality of minima, guarantees, generality But graph cuts use O(n) space vs O(mn) BP has better ties to statistics

Minima quality: graph cuts Data from [TF ICCV ’ 03 ]

Guarantees and generality n Graph cuts are better understood n n n Always converge to some kind of minimum Global, strong local, or weak local Depends on the class of problem This doesn’t make graph cuts a better method, just one we know more about LBP has gotten faster, graph cuts have gotten more general (just in the last year!)