Graph contd Some special simple graphs Complete Graphs

Graph (cont'd)

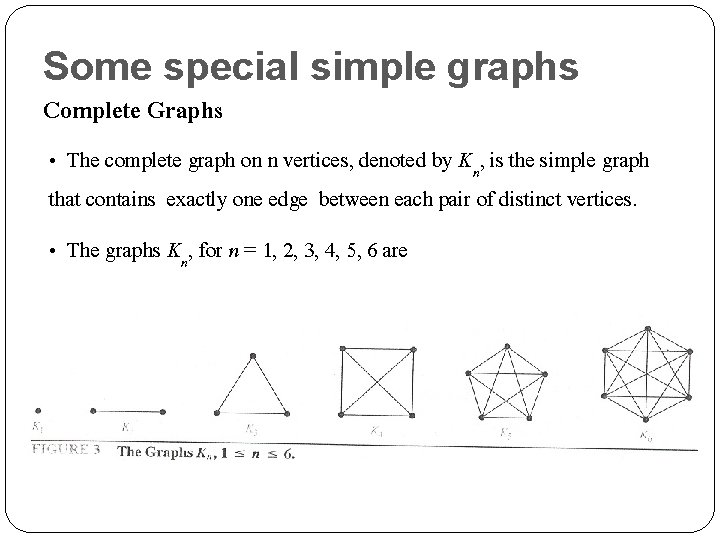
Some special simple graphs Complete Graphs • The complete graph on n vertices, denoted by Kn, is the simple graph that contains exactly one edge between each pair of distinct vertices. • The graphs Kn, for n = 1, 2, 3, 4, 5, 6 are

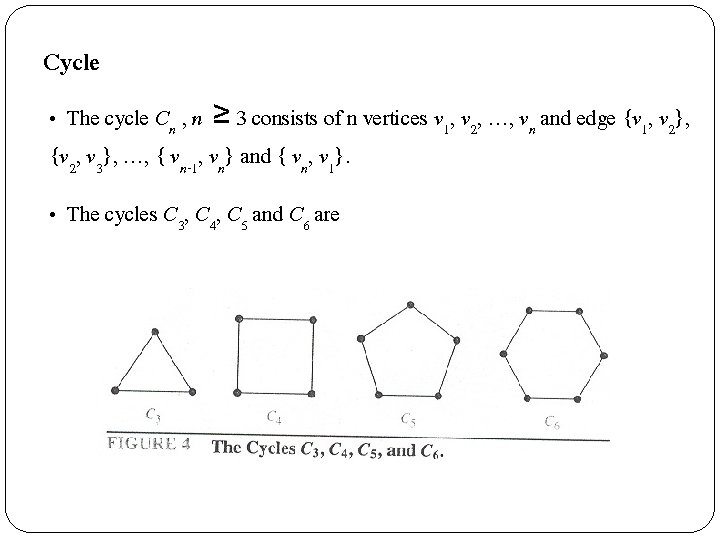
Cycle • The cycle Cn , n ≥ 3 consists of n vertices v 1, v 2, …, vn and edge {v 1, v 2}, {v 2, v 3}, …, { vn-1, vn} and { vn, v 1}. • The cycles C 3, C 4, C 5 and C 6 are

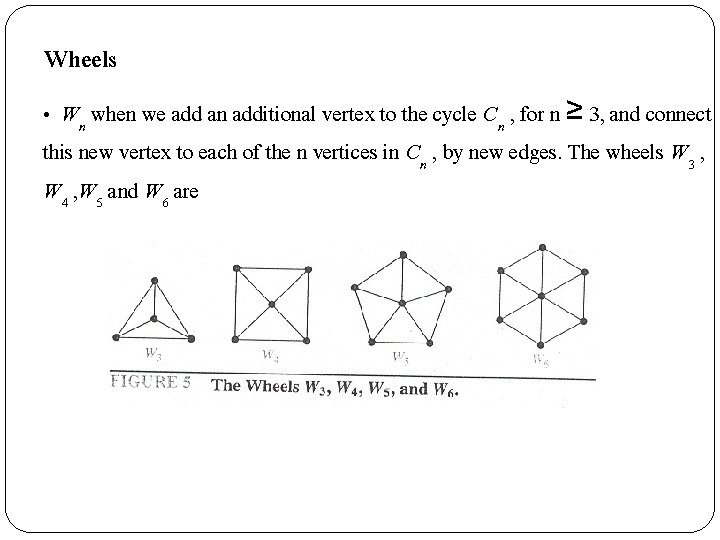
Wheels • Wn when we add an additional vertex to the cycle Cn , for n ≥ 3, and connect this new vertex to each of the n vertices in Cn , by new edges. The wheels W 3 , W 4 , W 5 and W 6 are

Bipartite Graph Definition • A simple graph G is called bipartite if its vertex set V can be partitioned into two disjoint nonempty sets V 1 and V 2 such that every edge in the graph connects a vertex in V 1 and vertex in V 2.

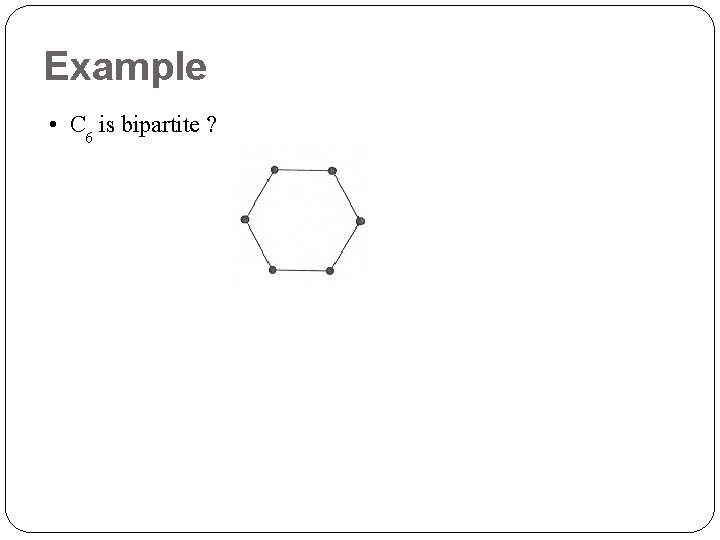
Example • C 6 is bipartite ?

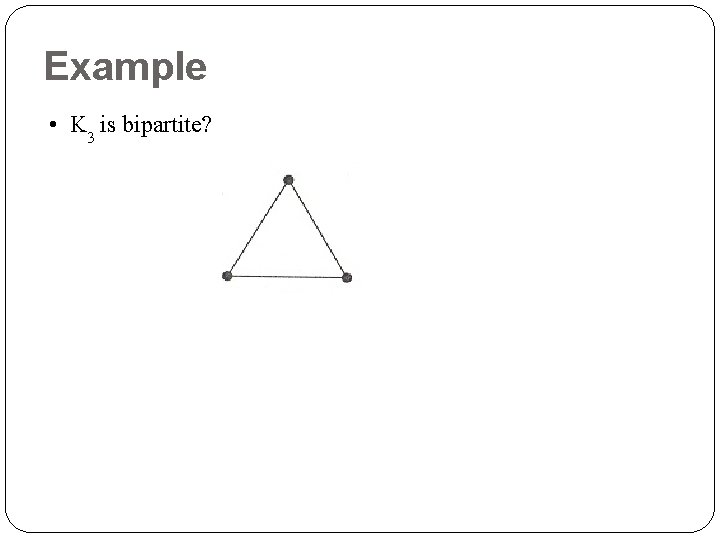
Example • K 3 is bipartite?

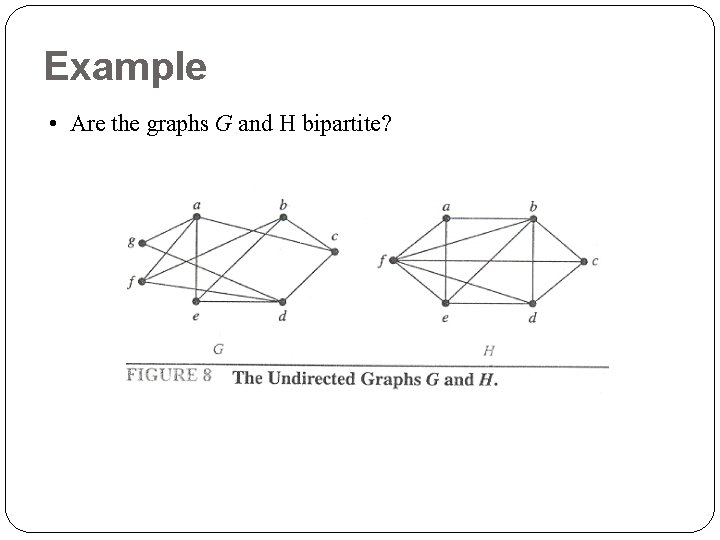
Example • Are the graphs G and H bipartite?

G: H:

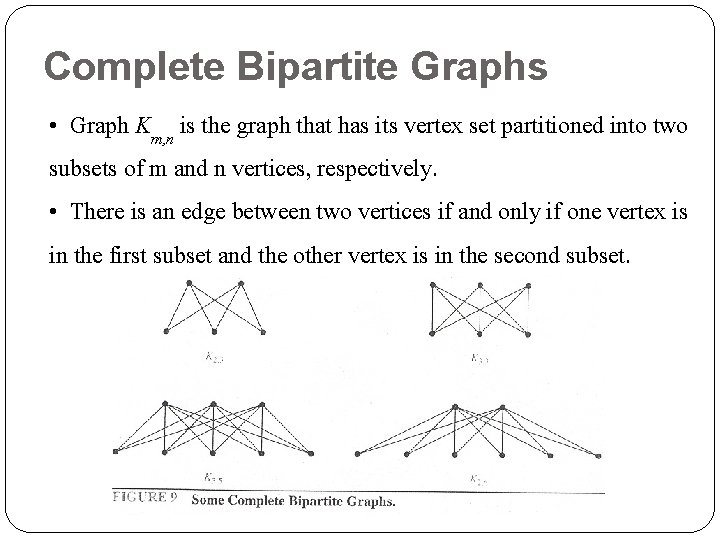
Complete Bipartite Graphs • Graph Km, n is the graph that has its vertex set partitioned into two subsets of m and n vertices, respectively. • There is an edge between two vertices if and only if one vertex is in the first subset and the other vertex is in the second subset.

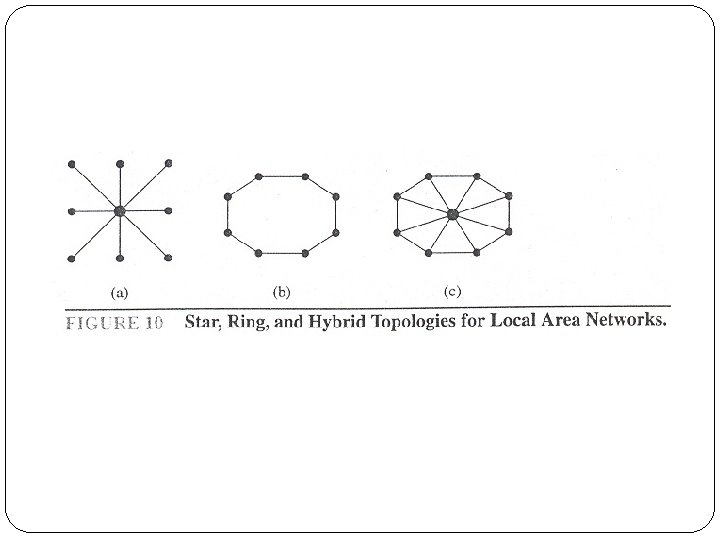
Application Local Area Networks The various computers in a building, such as minicomputers and personal computers, as well as peripheral devices such as printers and plotters, can be connected using a local area network.

q Star topology • All devices are connected to a central control device. • A local area network can be represented using a complete bipartite graph K 1, n. • Messages are sent from device to device through the central control device.

q Ring topology • each device is connected to exactly two others. • Local area networks with a ring topology are modeled using n-cycles, Cn. • Messages are sent from device to device around the cycle until the intended recipient of a message is reached.

q Hybrid topology • Messages may be sent around the ring, or through a central device. • Makes the network more reliable. • Local area networks with this redundancy can be modeled using wheels Wn.

Subgraph Definition • A subgraph of a graph G = (V, E) is a graph H = (W, F) where W V and F E.

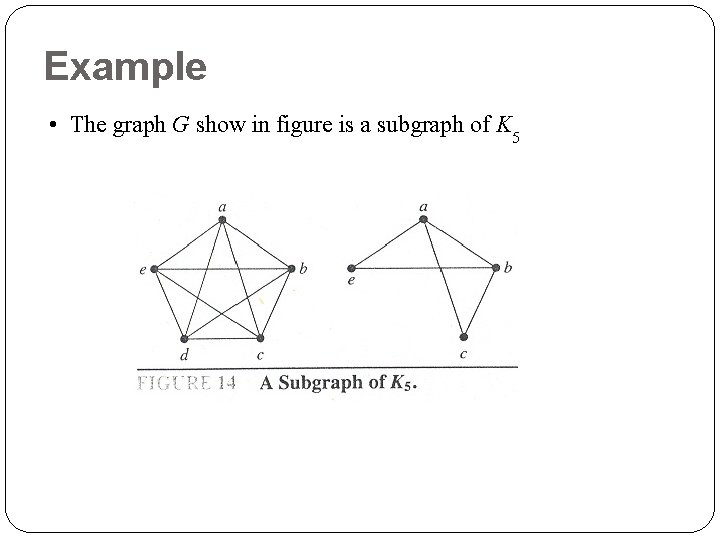
Example • The graph G show in figure is a subgraph of K 5

Union Definition • The union of two simple graphs G 1 = (V 1, E 1) and G 2 = (V 2, E 2) is the simple graph with vertex set V 1 V 2 and edge set E 1 U E 2. The union of G 1 and G 2 is denoted by G 1 G 2.

Example • Find the union of the graphs G 1 and G 2 show in figure. Solution