Graph Concepts Illustrated Using The Leda Library Amanuel

Graph Concepts Illustrated Using The Leda Library Amanuel Lemma CS 252 Algorithms

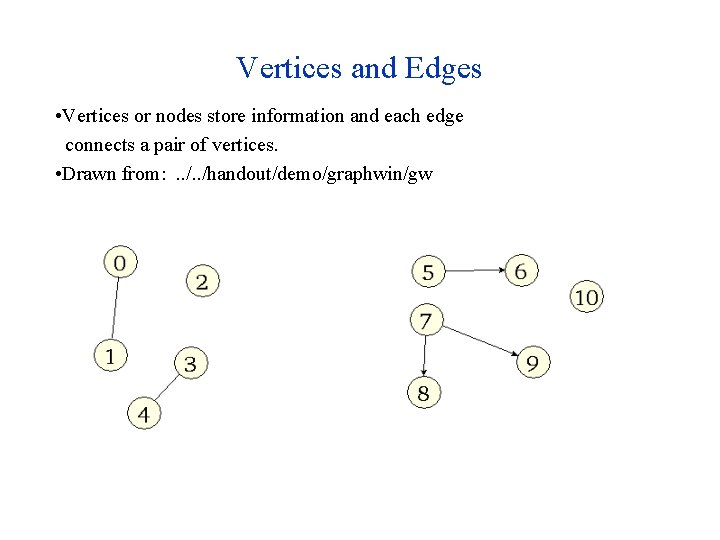
Vertices and Edges • Vertices or nodes store information and each edge connects a pair of vertices. • Drawn from: . . /handout/demo/graphwin/gw

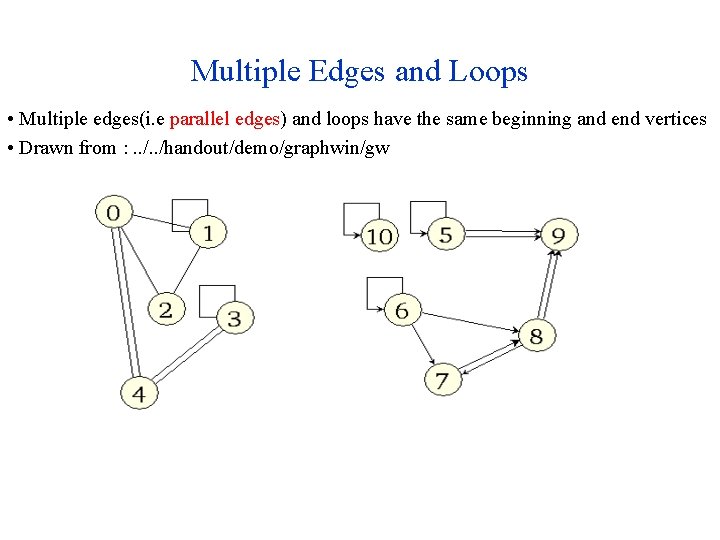
Multiple Edges and Loops • Multiple edges(i. e parallel edges) and loops have the same beginning and end vertices • Drawn from : . . /handout/demo/graphwin/gw

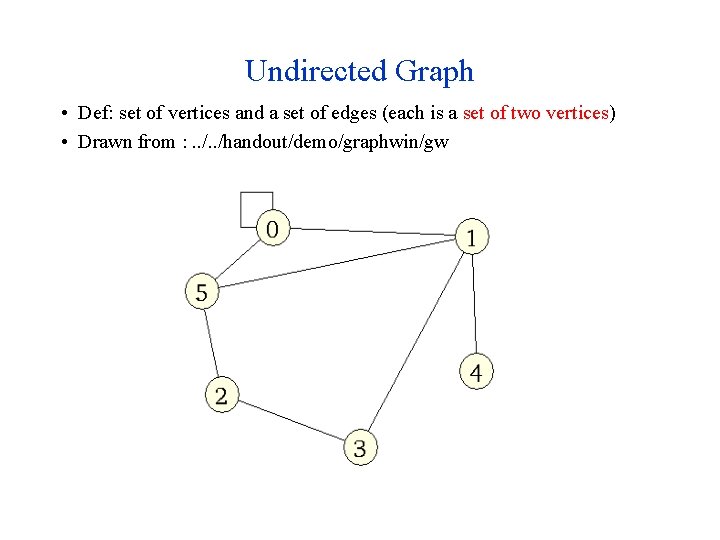
Undirected Graph • Def: set of vertices and a set of edges (each is a set of two vertices) • Drawn from : . . /handout/demo/graphwin/gw

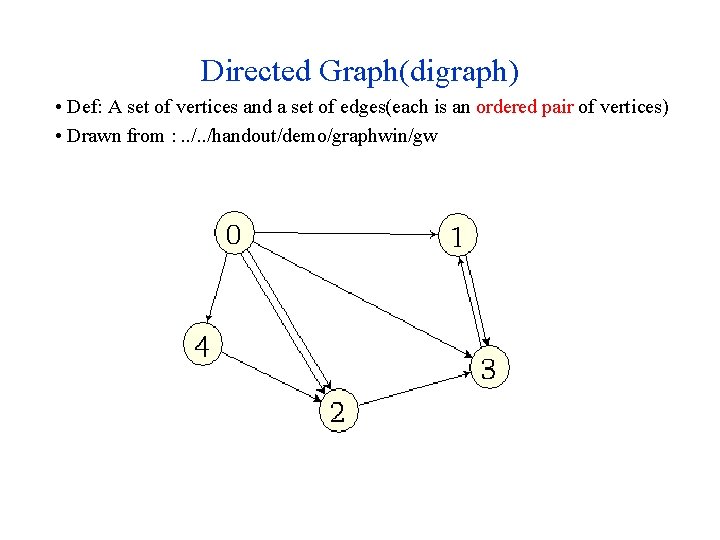
Directed Graph(digraph) • Def: A set of vertices and a set of edges(each is an ordered pair of vertices) • Drawn from : . . /handout/demo/graphwin/gw

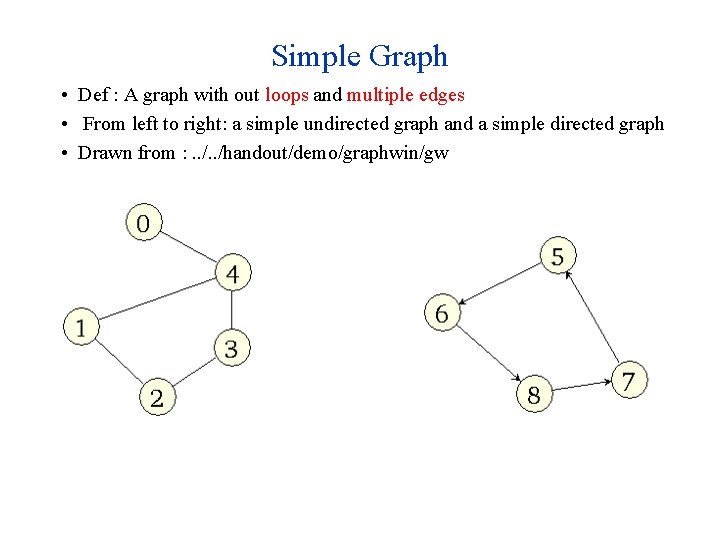
Simple Graph • Def : A graph with out loops and multiple edges • From left to right: a simple undirected graph and a simple directed graph • Drawn from : . . /handout/demo/graphwin/gw

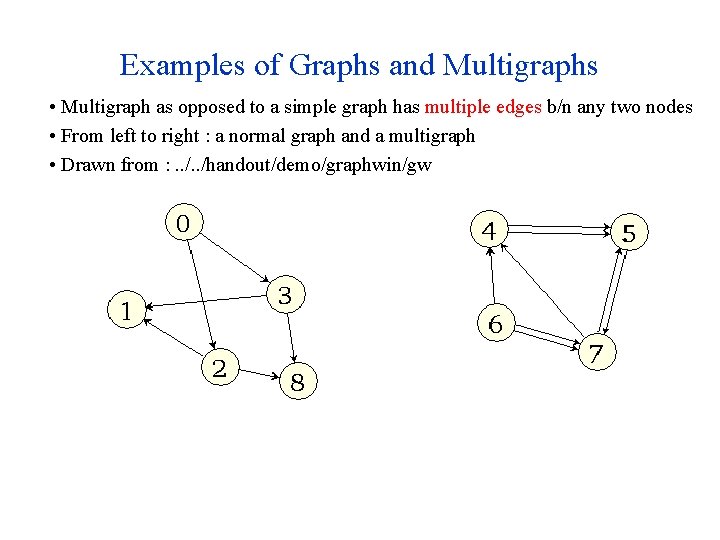
Examples of Graphs and Multigraphs • Multigraph as opposed to a simple graph has multiple edges b/n any two nodes • From left to right : a normal graph and a multigraph • Drawn from : . . /handout/demo/graphwin/gw

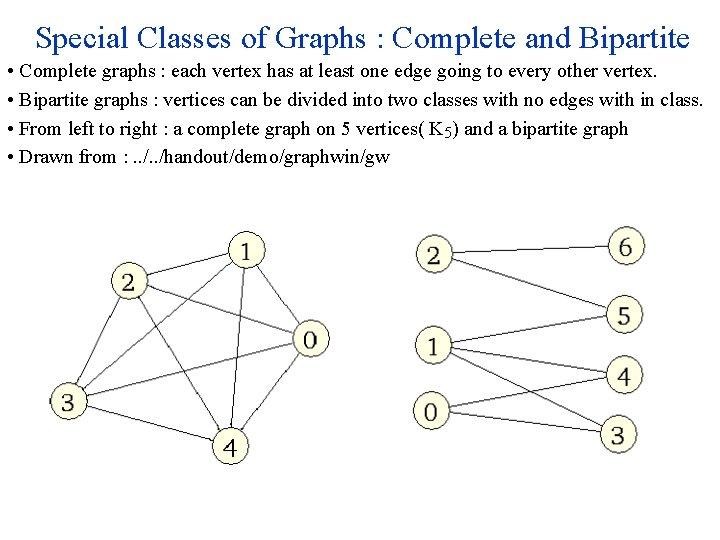
Special Classes of Graphs : Complete and Bipartite • Complete graphs : each vertex has at least one edge going to every other vertex. • Bipartite graphs : vertices can be divided into two classes with no edges with in class. • From left to right : a complete graph on 5 vertices( K 5) and a bipartite graph • Drawn from : . . /handout/demo/graphwin/gw

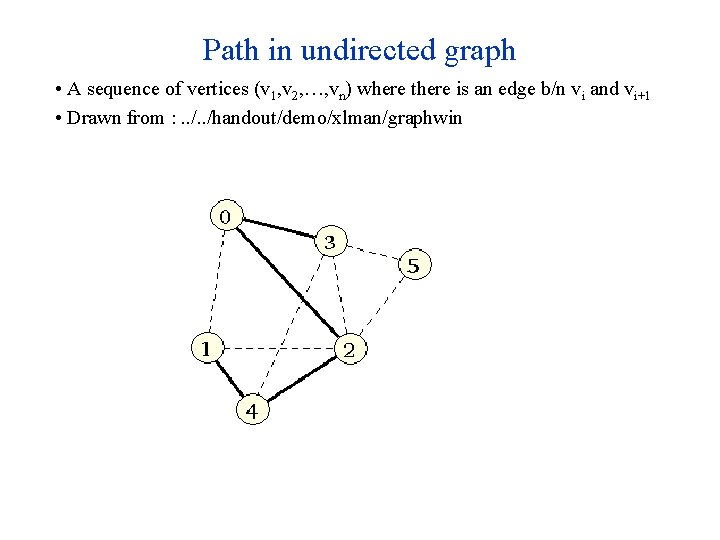
Path in undirected graph • A sequence of vertices (v 1, v 2, …, vn) where there is an edge b/n vi and vi+1 • Drawn from : . . /handout/demo/xlman/graphwin

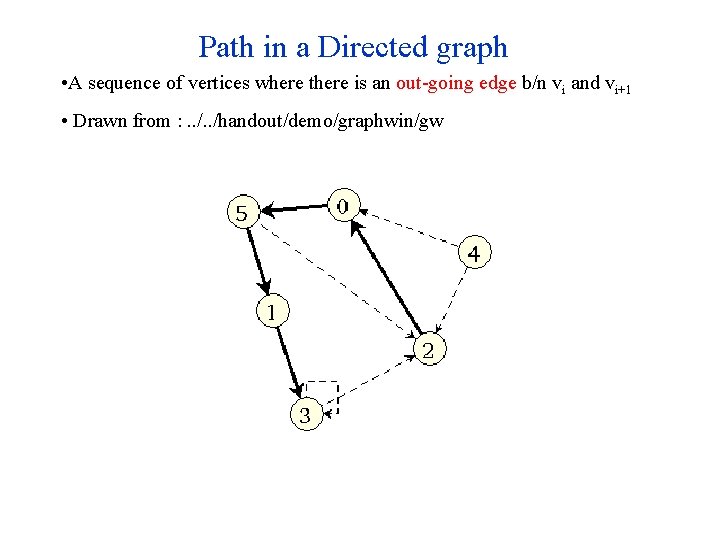
Path in a Directed graph • A sequence of vertices where there is an out-going edge b/n vi and vi+1 • Drawn from : . . /handout/demo/graphwin/gw

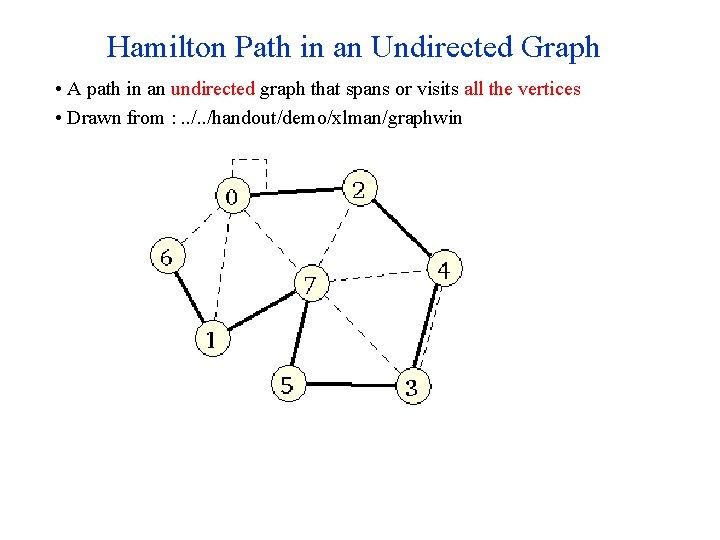
Hamilton Path in an Undirected Graph • A path in an undirected graph that spans or visits all the vertices • Drawn from : . . /handout/demo/xlman/graphwin

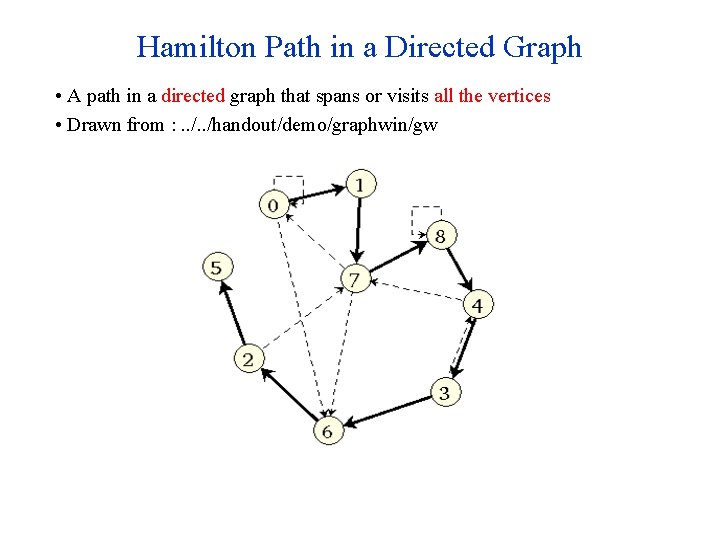
Hamilton Path in a Directed Graph • A path in a directed graph that spans or visits all the vertices • Drawn from : . . /handout/demo/graphwin/gw

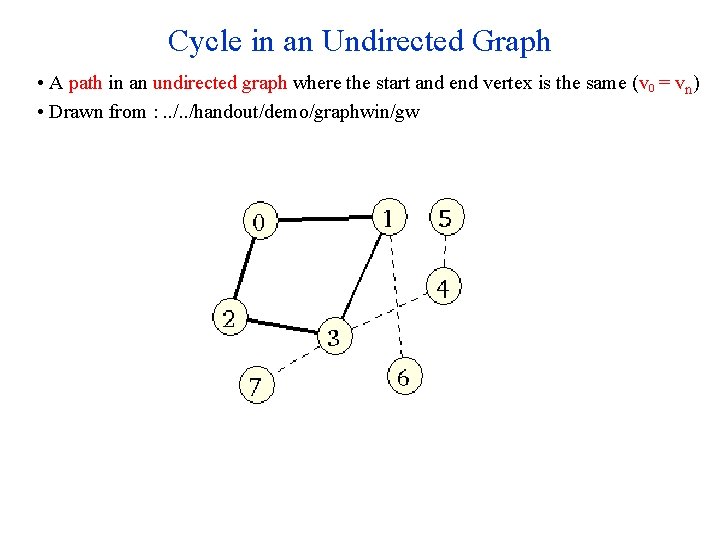
Cycle in an Undirected Graph • A path in an undirected graph where the start and end vertex is the same (v 0 = vn) • Drawn from : . . /handout/demo/graphwin/gw

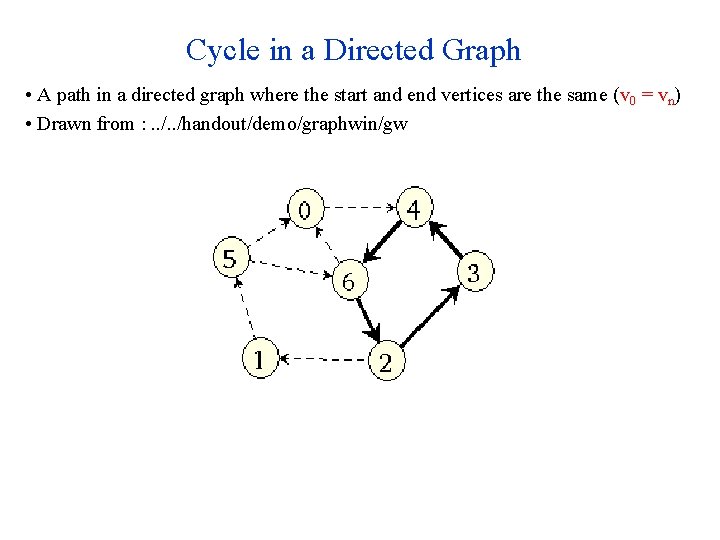
Cycle in a Directed Graph • A path in a directed graph where the start and end vertices are the same (v 0 = vn) • Drawn from : . . /handout/demo/graphwin/gw

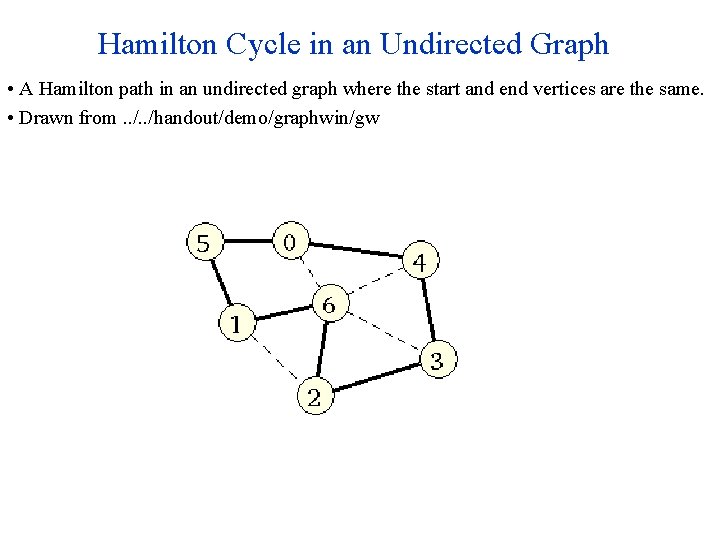
Hamilton Cycle in an Undirected Graph • A Hamilton path in an undirected graph where the start and end vertices are the same. • Drawn from. . /handout/demo/graphwin/gw

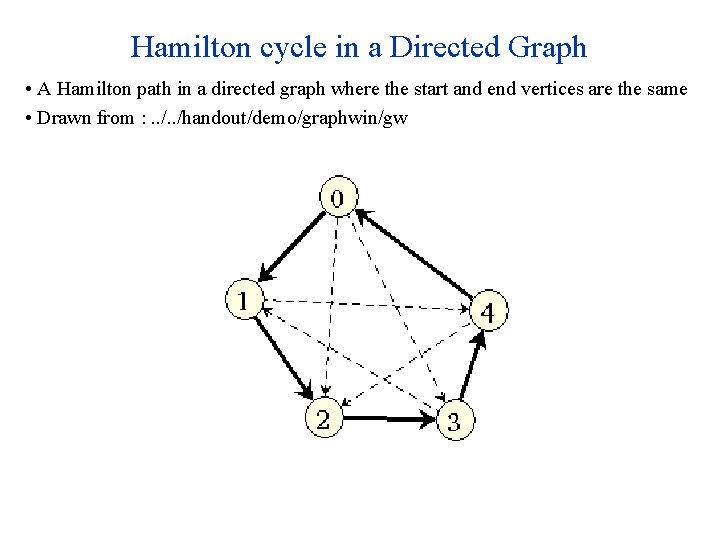
Hamilton cycle in a Directed Graph • A Hamilton path in a directed graph where the start and end vertices are the same • Drawn from : . . /handout/demo/graphwin/gw

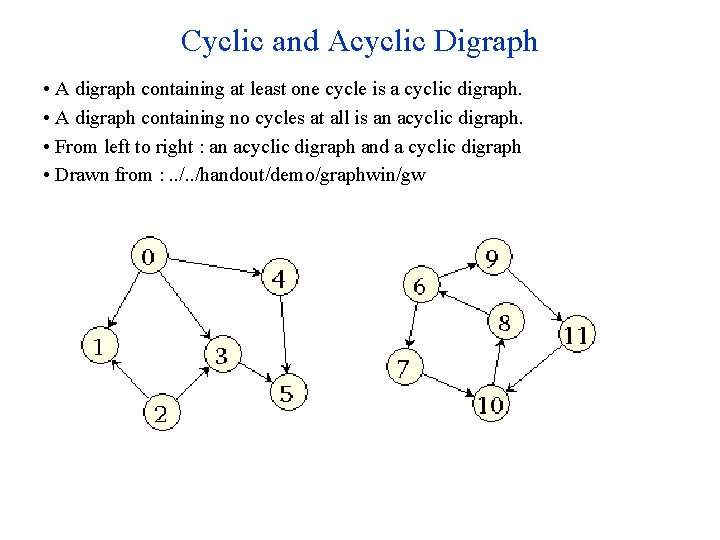
Cyclic and Acyclic Digraph • A digraph containing at least one cycle is a cyclic digraph. • A digraph containing no cycles at all is an acyclic digraph. • From left to right : an acyclic digraph and a cyclic digraph • Drawn from : . . /handout/demo/graphwin/gw

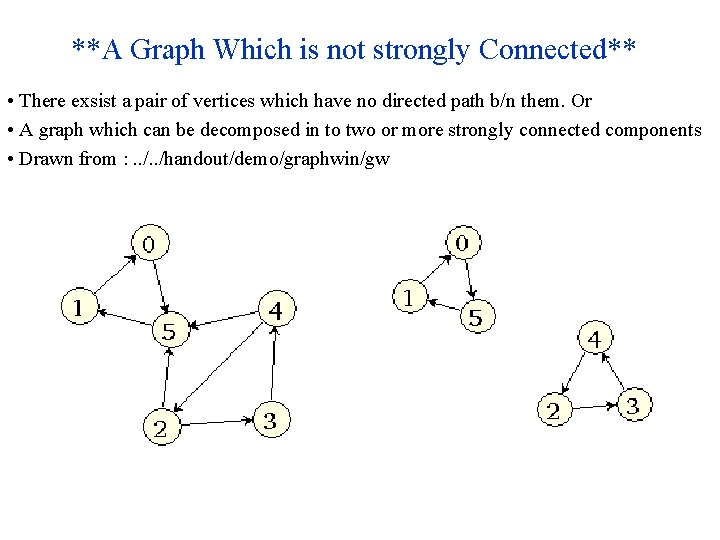
**A Graph Which is not strongly Connected** • There exsist a pair of vertices which have no directed path b/n them. Or • A graph which can be decomposed in to two or more strongly connected components • Drawn from : . . /handout/demo/graphwin/gw

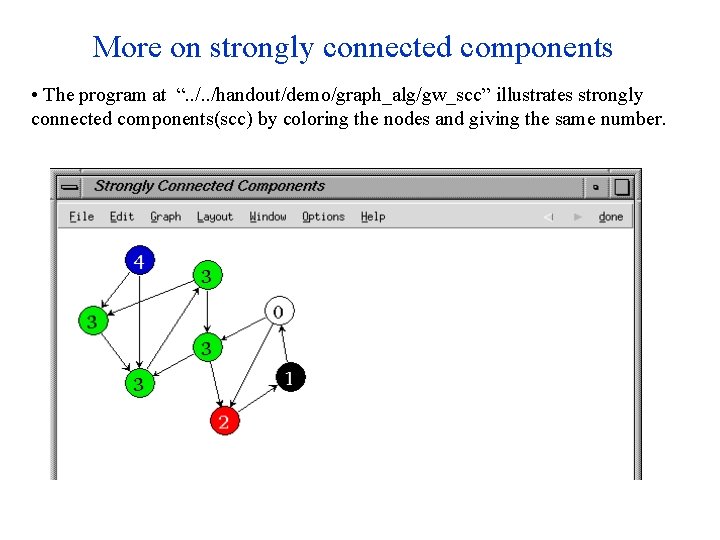
More on strongly connected components • The program at “. . /handout/demo/graph_alg/gw_scc” illustrates strongly connected components(scc) by coloring the nodes and giving the same number.

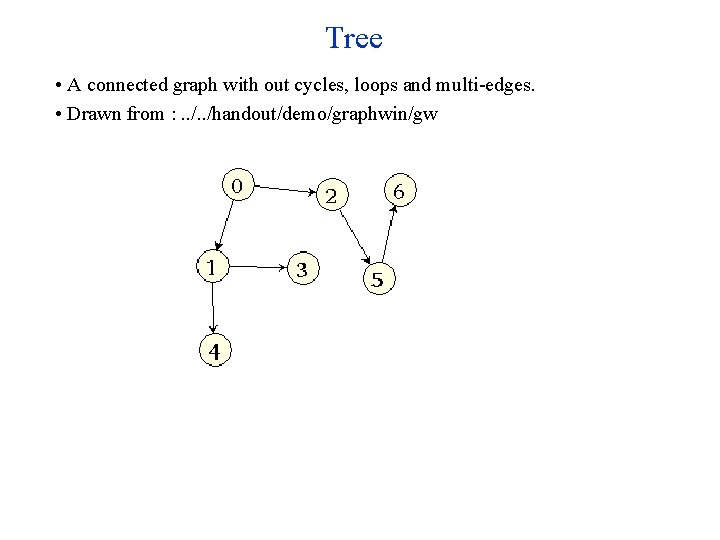
Tree • A connected graph with out cycles, loops and multi-edges. • Drawn from : . . /handout/demo/graphwin/gw

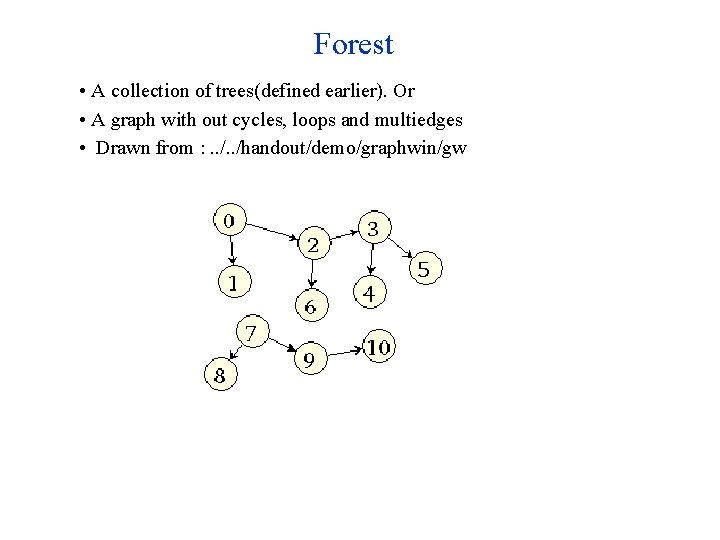
Forest • A collection of trees(defined earlier). Or • A graph with out cycles, loops and multiedges • Drawn from : . . /handout/demo/graphwin/gw