Graph Concepts and Algorithms Using LEDA By Caroline

Graph Concepts and Algorithms Using LEDA By Caroline Moore and Carmen Frerichs (252 a-at and 252 a-ao) each graph in the presentation was created using gw_basic_graph_algorithms

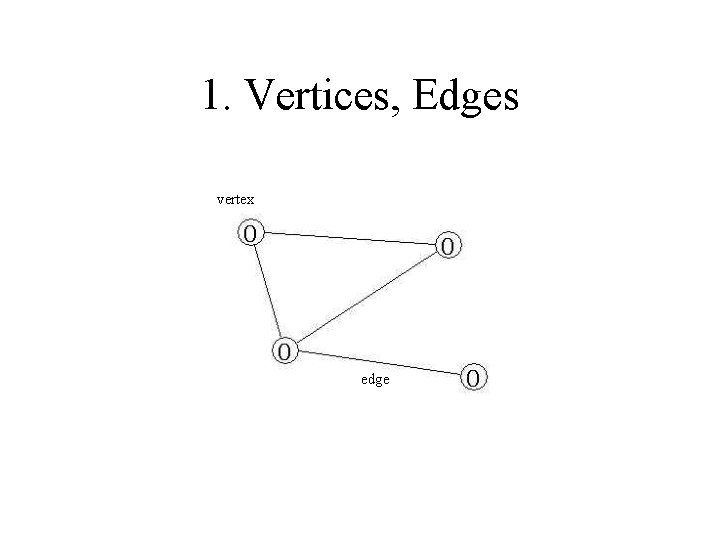
1. Vertices, Edges vertex edge

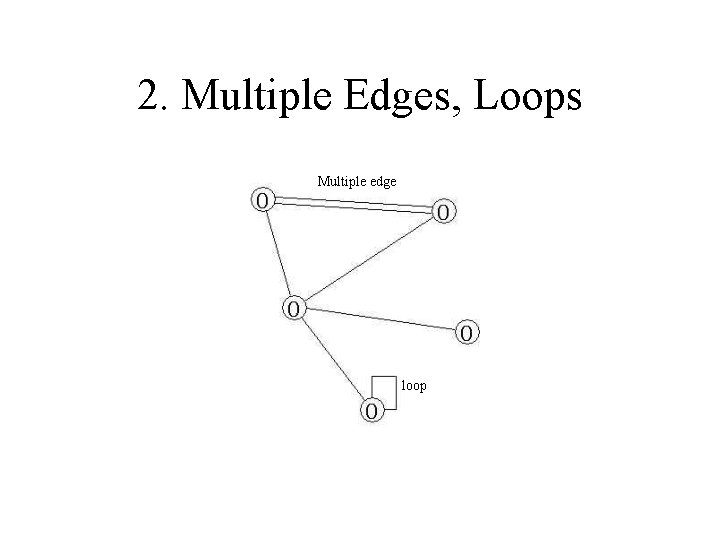
2. Multiple Edges, Loops Multiple edge loop

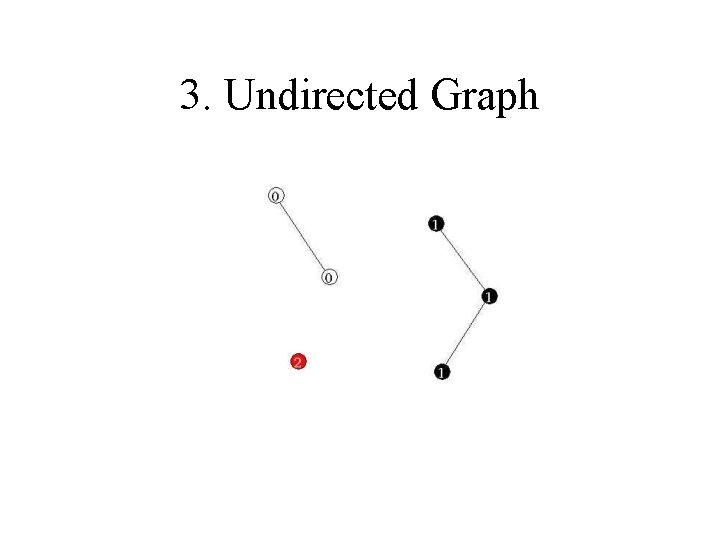
3. Undirected Graph

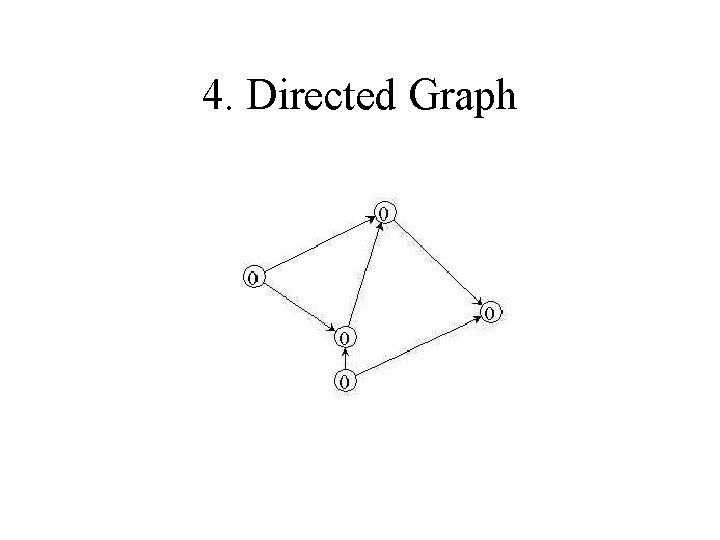
4. Directed Graph

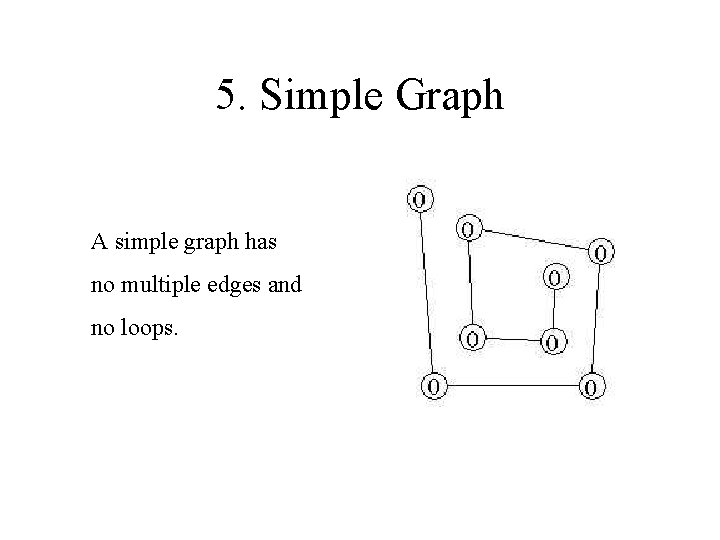
5. Simple Graph A simple graph has no multiple edges and no loops.

6. Examples of graphs and multigraphs This is both a graph and a multigraph (multigraph is a graph containing multiple edges) Multiple edge

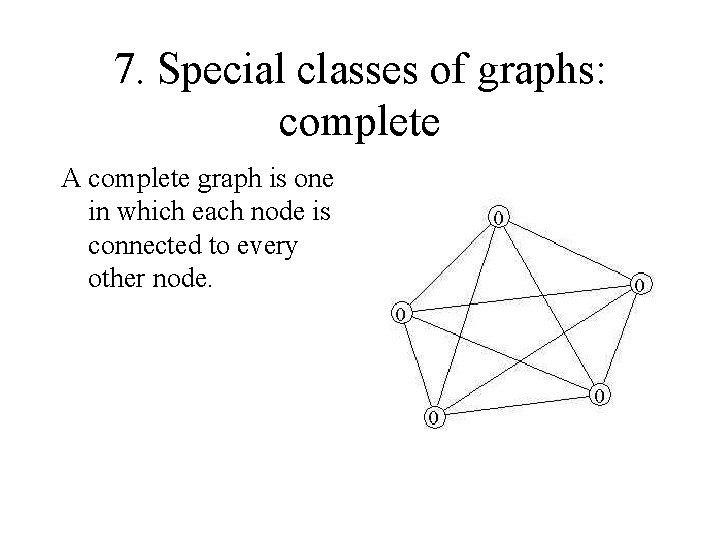
7. Special classes of graphs: complete A complete graph is one in which each node is connected to every other node.

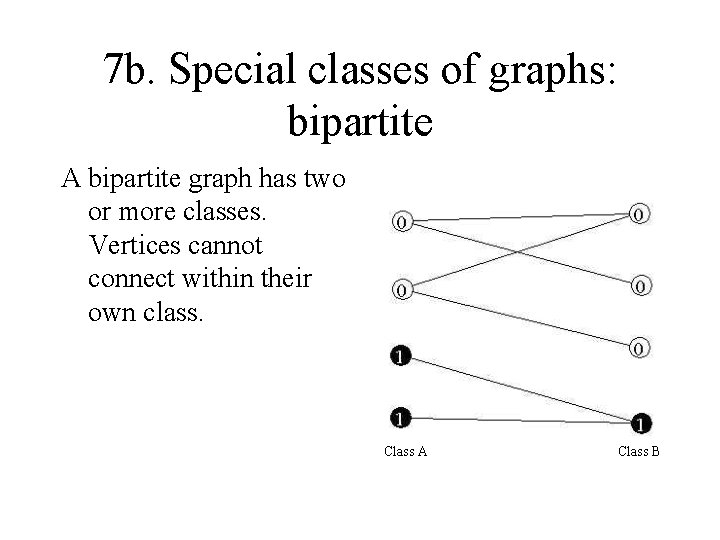
7 b. Special classes of graphs: bipartite A bipartite graph has two or more classes. Vertices cannot connect within their own class. Class A Class B

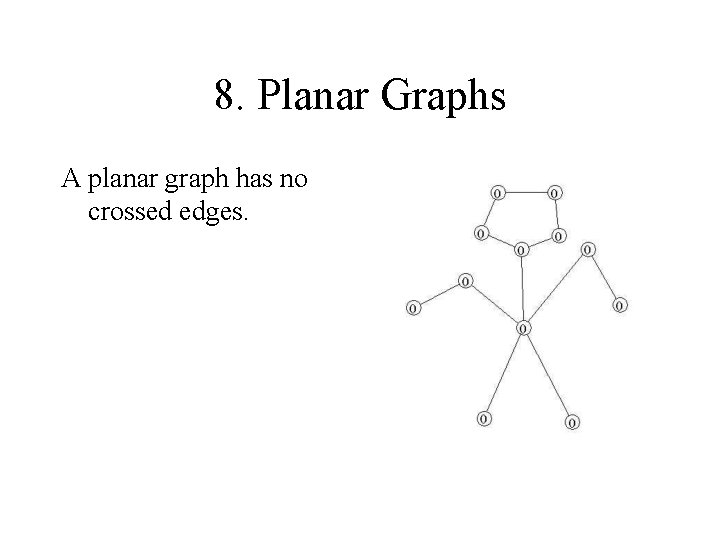
8. Planar Graphs A planar graph has no crossed edges.

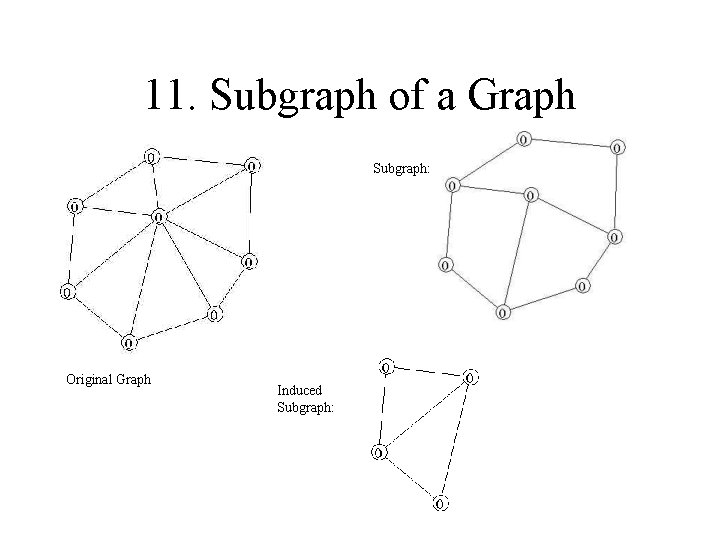
11. Subgraph of a Graph Subgraph: Original Graph Induced Subgraph:

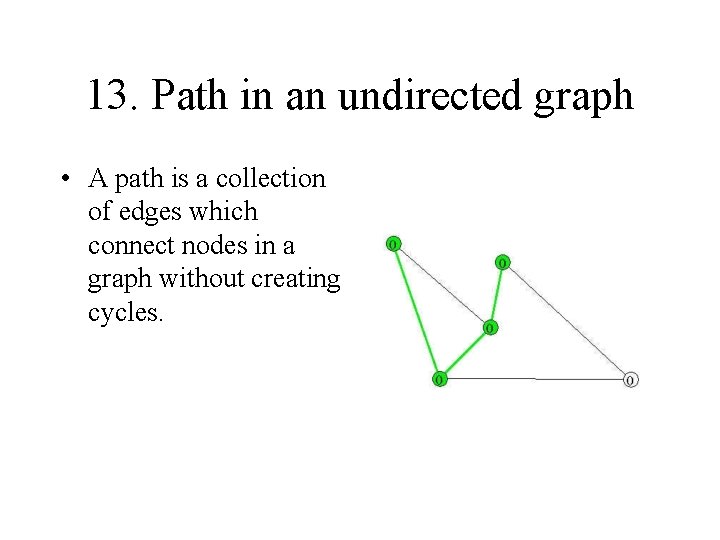
13. Path in an undirected graph • A path is a collection of edges which connect nodes in a graph without creating cycles.

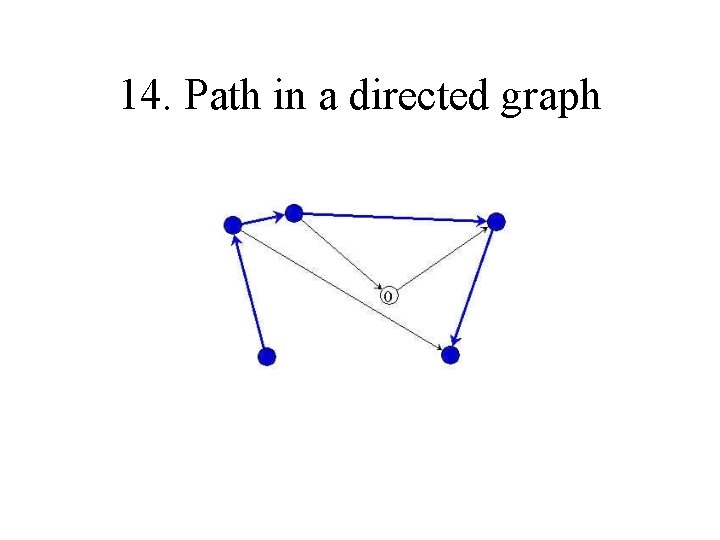
14. Path in a directed graph

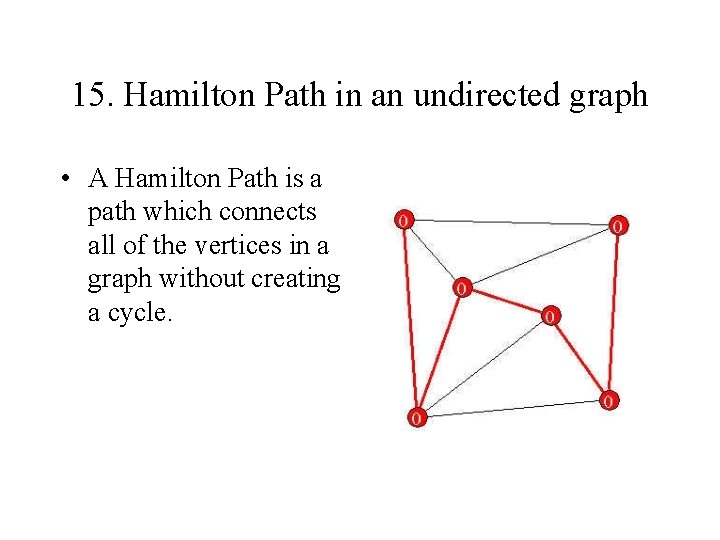
15. Hamilton Path in an undirected graph • A Hamilton Path is a path which connects all of the vertices in a graph without creating a cycle.

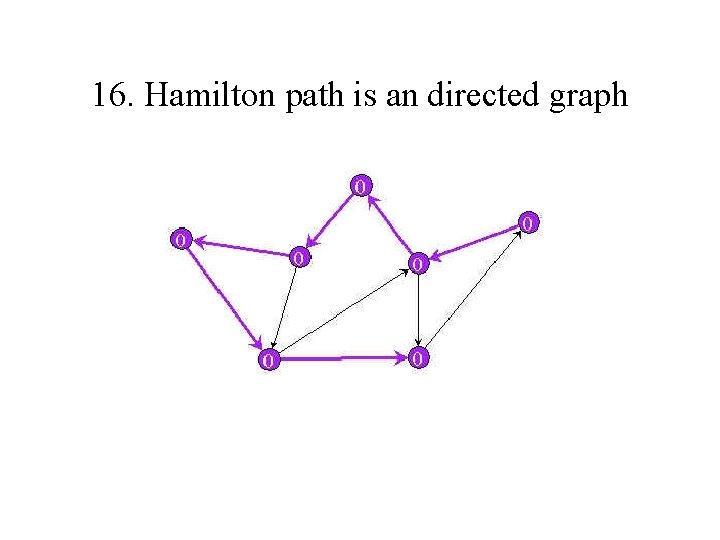
16. Hamilton path is an directed graph

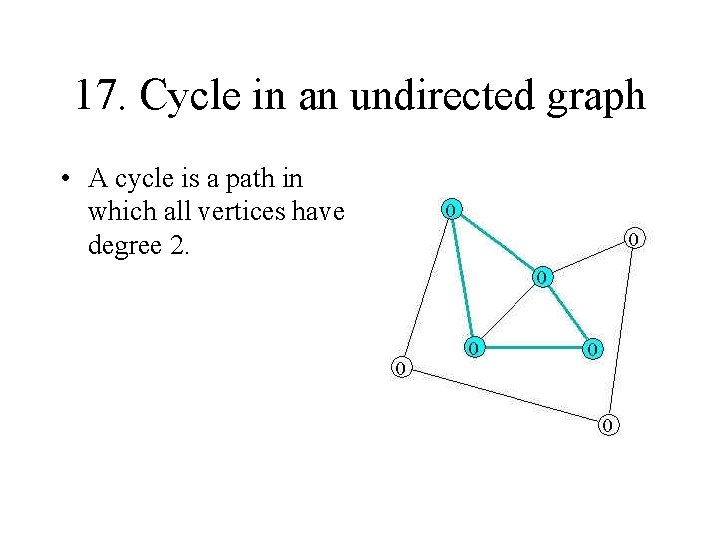
17. Cycle in an undirected graph • A cycle is a path in which all vertices have degree 2.

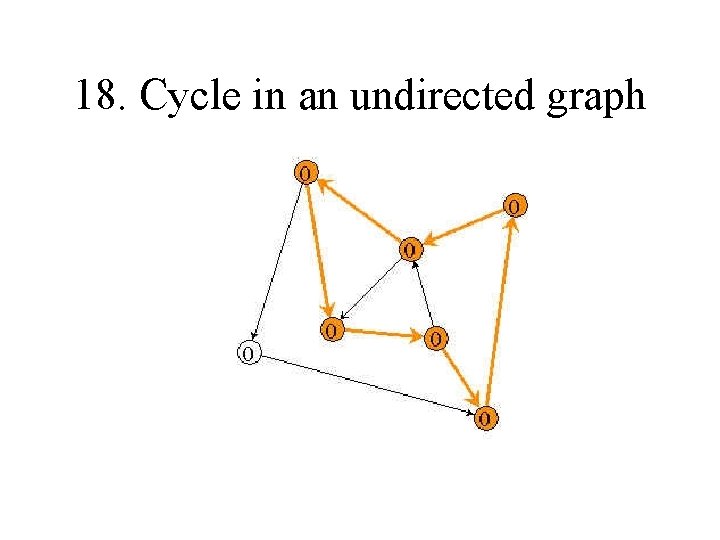
18. Cycle in an undirected graph

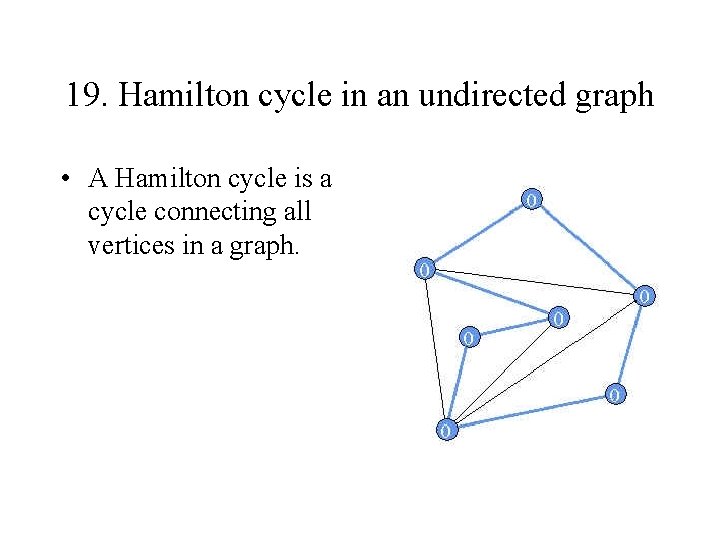
19. Hamilton cycle in an undirected graph • A Hamilton cycle is a cycle connecting all vertices in a graph.

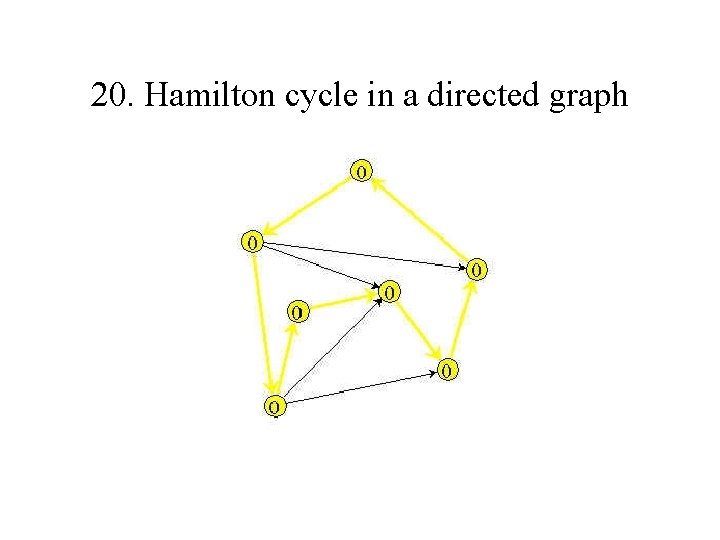
20. Hamilton cycle in a directed graph

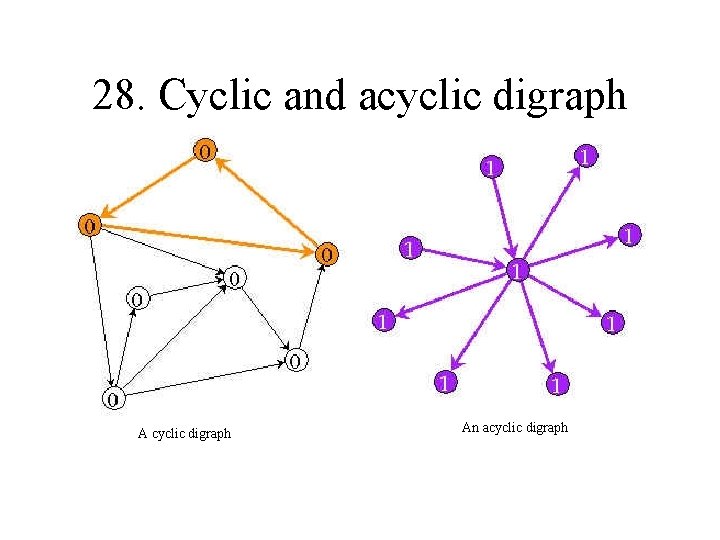
28. Cyclic and acyclic digraph An acyclic digraph

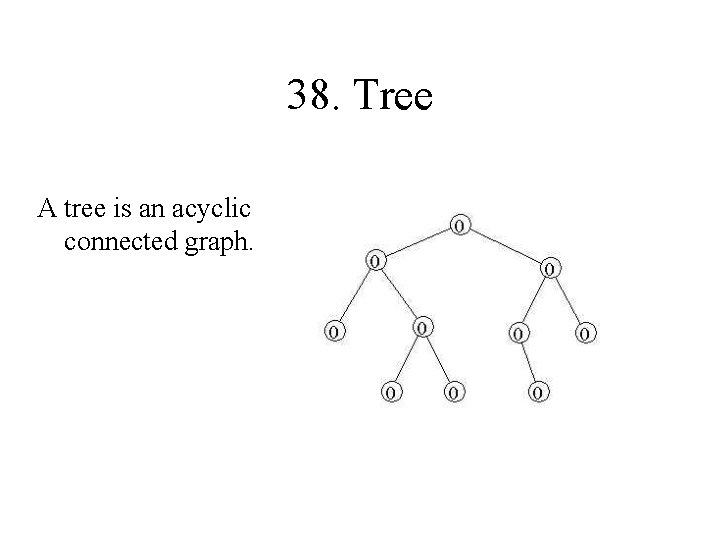
38. Tree A tree is an acyclic connected graph.

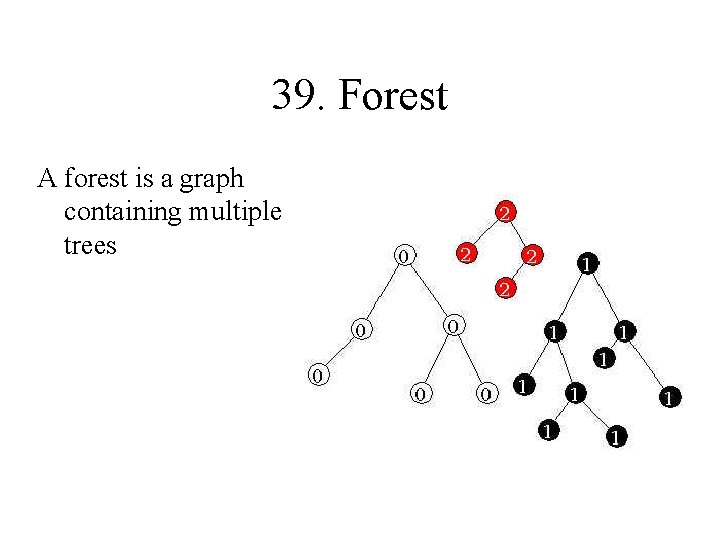
39. Forest A forest is a graph containing multiple trees