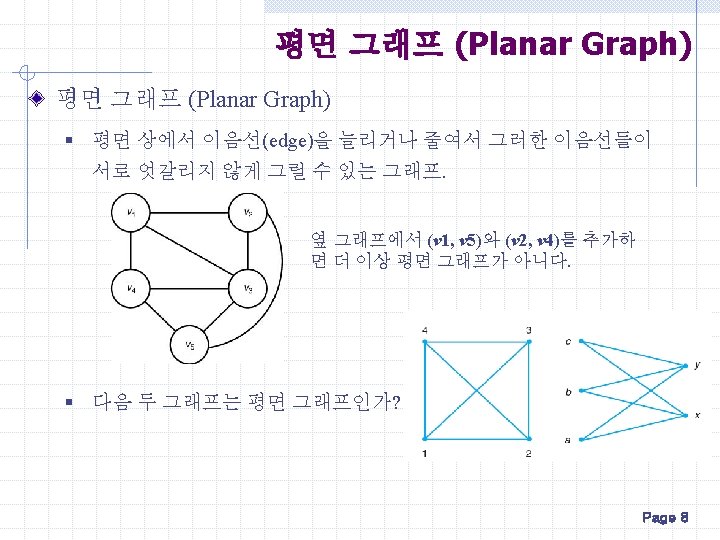
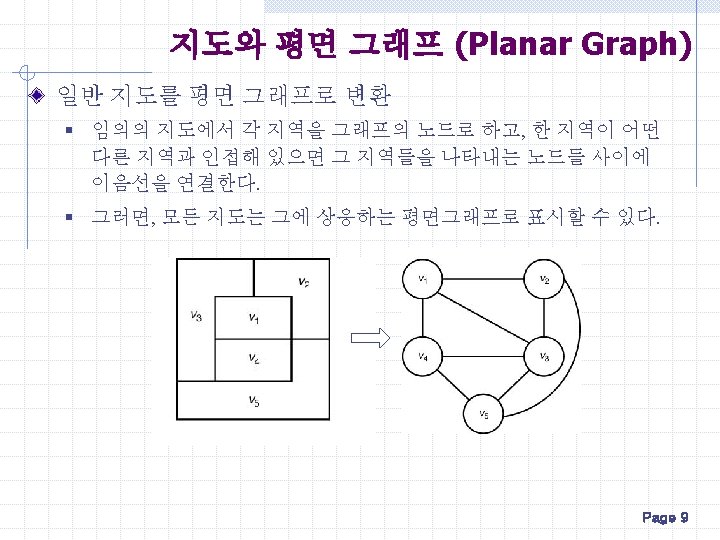
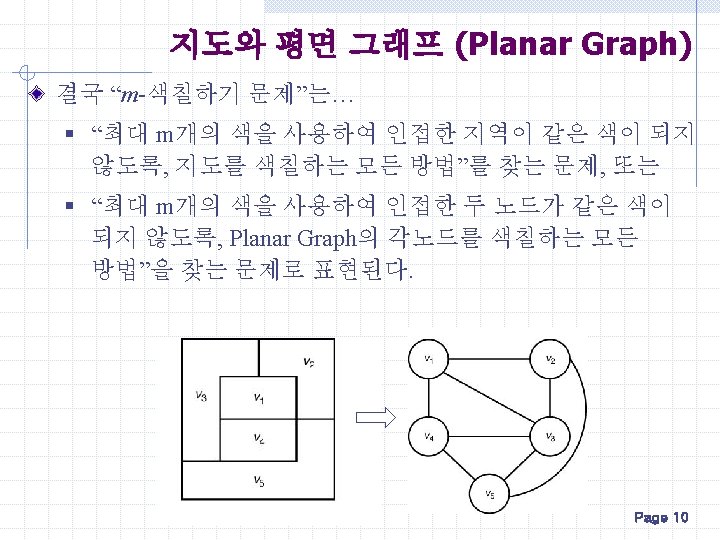
Graph Coloring Backtracking Strategy for 3 Coloring Problem

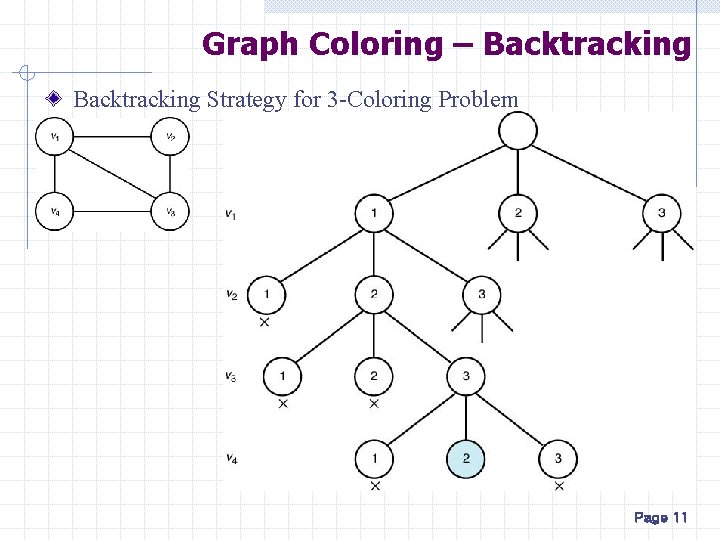
Graph Coloring – Backtracking Strategy for 3 -Coloring Problem Page 11

Graph Coloring – Algorithm (1/2) A Backtracking Algorithm for the Graph Coloring Problem • 입력: n – 노드의 수, m – 색깔의 수, W[i][j] – 이음선 있으면 true, 그렇지 않으면 false • 출력: vcolor[i] - i번째 노드에 할당된 색(1 ~ m) void m_coloring(index i){ int color; if(promising(i)) if(i == n) System. out. print(vcolor[1] through vcolor[n]); else for(color = 1; color <= m; color++) { vcolor[i+1] = color; //다음 노드에 모든 색을 시도해 본다. m_coloring(i+1); } } 최상위 수준 호출: m_coloring(0); Page 12

Graph Coloring – Algorithm (2/2) A Backtracking Algorithm for the Graph Coloring Problem (계속) boolean promising(index i){ index j = 1; boolean switch = true; while(j < i && switch) { if(W[i][j] && vcolor[i] == vcolor[j]) switch = false; j++; } return switch; } vertex i 보다 작은 모든 vertex j에 대해 “인접하고, 색이 같은지”의 여부를 조사한다. Page 13

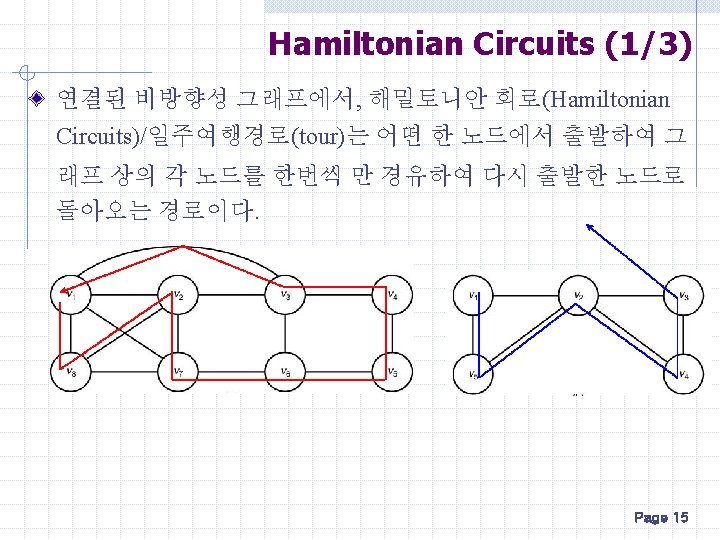
Hamiltonian Circuits (2/3) TSP Problem Hamiltonian Circuits Problem Given a graph G with weighted edges, the problem of finding the Hamiltonian cycle of smallest possible weight is called the traveling salesman problem (TSP) on G. List of half of all possible Hamiltonian cycles, (for each route, the reverse route has the same cost) Page 16