Graph Coalition Structure Generation Maria Polukarov University of

Graph Coalition Structure Generation Maria Polukarov University of Southampton Joint work with Tom Voice and Nick Jennings HUJI, 25 th September 2011

Outline Coalition Structure Generation (CSG) ü Complete Set Partitioning CSG over graphs (GCSG) ü Clustering ü Graph Partitioning Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs 2

Outline Coalition Structure Generation (CSG) ü Complete Set Partitioning CSG over graphs (GCSG) ü Clustering ü Graph Partitioning Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs 3

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) ü Clustering ü Graph Partitioning Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs 4

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) ü Clustering ü Graph Partitioning Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs 5

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) ü Clustering ü Graph Partitioning Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs 6

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs Future directions 7

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs Future directions 8

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs Future directions 9

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs Future directions 10

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) Independence of disconnected members (IDM) Results ü General graphs ü Bounded treewidth graphs ü Planar graphs Future directions 11

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) Independence of disconnected members (IDM) Results Future directions 12

Outline Coalition Structure Generation (CSG) CSG over graphs (GCSG) Independence of disconnected members (IDM) Results Future directions 13

Model

Coalition Structure Generation 15

Coalition Structure Generation 16

Coalition Structure Generation 17

Coalition Structure Generation 18

CSG [notation] N = {1, …, n} – set of elements (``agents’’) v: P(N) R – characteristic function CSG problem: find partition {N 1, …, Nm} of N that maximizes Σiv(Ni) 19

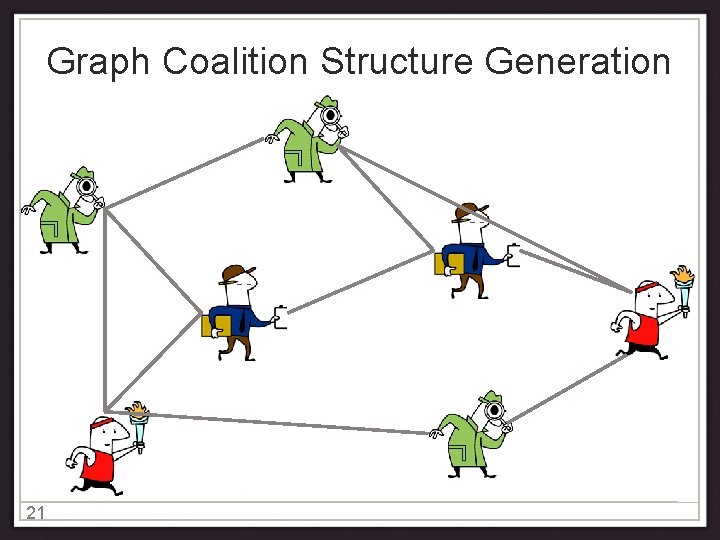
Graph Coalition Structure Generation 21

Independence of disconnected members (IDM) For a graph G = (N, E), a function v: P(N) R is IDM if for all with , and a coalition not containing i and j, 22

IDM [examples] Each edge (i, j) has a constant weight vij. The edge sum characteristic function I is IDM. Each edge is labelled by + or – , and let The correlation characteristic function is IDM. 23

IDM [properties] Lemma: Given a graph G=(N, E) and an IDM coalition valuation function v(), for any two subsets of nodes A, B, if there are no edges between AB and BA then 24

IDM For a graph G = (N, E), a coalition structure C over N is connected if the induced subgraph of G is connected for all coalitions C in C. Remark: for an IDM function v and a coalition structure C, there exists a connected structure D such that v(C) = v(D). Moreover, if G is not connected, the problem is solved by finding the optimal structure over each connected component of G and combining the results. 25

GCSG Given a connected graph G=(N, E) and an IDM characteristic function v: P(N) R, the Graph Coalition Structure Generation problem over G is to maximize for C a coalition structure over N. This problem is equivalent to maximizing the same objective function over all connected coalition structures. 26

Remark Clustering problems in general do not necessarily fit in our model: ü some of them have objectives that do not admit the IDM property (e. g. , modularity clustering) ü some clustering problems have additional restrictions on feasible graph partitions (e. g. , weighted graph partitioning) 27

Results

General graphs The GCSG problem is NP-complete on general graphs, even for edge sum characteristic functions A general instance with |N|=n nodes and |E|=e edges can be solved in time using O(n 2) memory For sparse graphs with e=cn edges, where c is a constant, this implies the bound of with a constant 29

Minor free graphs We give general bounds on the computational complexity of the GCSG problem for planar graphs and, more generally, minor free graphs. We show polynomial time solvability of the GCSG problem for bounded treewidth graphs. We prove NP-hardness for planar, and hence, all Kk minor free graphs for k ≥ 5, even for edge sum characteristic functions. 30

Separator theorems A class of graphs S satisfies an f(n)-separator theorem with constant α < 1 if for all G = (N, E) in S with |N| = n there exist two subgraphs A, B of G such that , the number of nodes in is less than or equal to f(n) and both the number of nodes in AB and the number of nodes in BA are ≤ αn. 31

Separator theorems Suppose a class of graphs S is closed under taking subgraphs and there is an increasing function g(n) such that for all G = (N, E) in S with |N| = n, graph G has at most g(n) possible connected coalition structures. Suppose that S satisfies an f(n)-separator theorem with constant α < 1, and that for any G such a separator can be found in time, where f(n) is an increasing o(n) function and 32

Separator theorems Theorem: For any α < β < 1, an instance of the graph coalition structure generation problem over a graph from S can be solved in I computation steps. 33

Separator theorems Corollary: 34

Bounds for minor free and planar graphs Theorem: For any graph H with k vertices and , an instance of the graph coalition structure generation problem over an H minor free graph G with n nodes requires computation steps. Theorem: For any , a general instance of a graph coalition structure generation problem over a planar graph G with n nodes can be solved in computation steps. 35

Bounded treewidth graphs Theorem: A GCSG problem over the class of graphs of maximum treewidth k can be solved in O(n 2) time, for any k. 36

Bounded treewidth graphs Theorem: A GCSG problem over the class of graphs of maximum treewidth k can be solved in O(n) time, for any k. 37

Tree decompositions Theorem: A general instance of the graph coalition structure generation problem over a graph G with n nodes and a known tree decomposition of width w can be solved in I computation steps. 38

Tree decompositions Lemma: Given a graph G=(N, E) and a tree decomposition (X, T), where X={X 1, …, Xm} for m≤n and T is a tree over X. Suppose further that the Xis are numbered in order of shortest distance in T from X 1 which can be chosen arbitrarily. Then, for any subset of nodes C, 39

Tree decompositions 40

Tree decompositions Lemma: 41

Tree decompositions We prove the bound of by recursively calculating the potential marginal contributions to total coalition structure value for branches of the tree. Given any constant k, for the class of graphs with maximum treewidth k, a tree decomposition with width at most k can be found in time linear in n, and so the bound of O(n) for the GCSG follows. 42

Separator theorems Lemma: 43

Bounds for minor free and planar graphs Theorem: For any graph H with k vertices, an instance of the graph coalition structure generation problem over an H minor free graph G with n nodes requires computation steps for Theorem: A general instance of a graph coalition structure generation problem over a planar graph G with n nodes can be solved in computation steps, for Ø Exponential in it can get! , but is almost as good as 44

Planar graphs Theorem: The class of edge sum graph coalition structure generation problems over planar graphs is NP-complete. Moreover, a 3 -SAT problem with m clauses can be represented by a GCSG problem over a planar graph with O(m 2) nodes. 45

Planar graphs Proof (short sketch): • Given a 3 -SAT problem with clauses C 1, …, Cm, we construct an edge sum GCSG problem over a planar graph of O(m 2) nodes which, when solved, reveals a solution to the 3 -SAT problem if one exists. • This graph has components of 5 types. 46

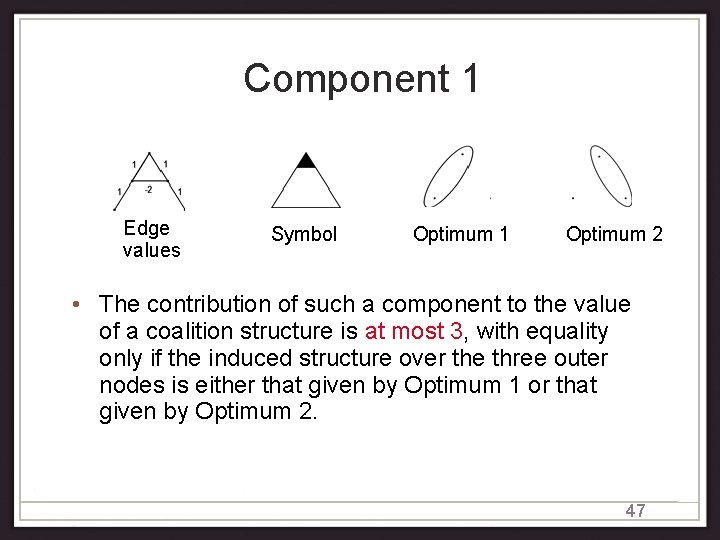
Component 1 Edge values Symbol Optimum 1 Optimum 2 • The contribution of such a component to the value of a coalition structure is at most 3, with equality only if the induced structure over the three outer nodes is either that given by Optimum 1 or that given by Optimum 2. 47

Components 2 and 3 • Similarly, we define two more triangular components Edge values Symbol Edge values Optimum 1 Symbol Optimum 2 Optimum 3 Optimum 48

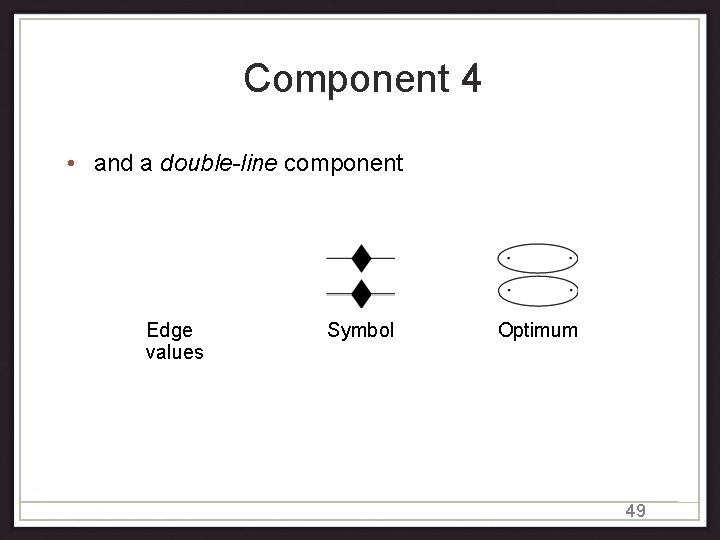
Component 4 • and a double-line component Edge values Symbol Optimum 49

Component 5 Construction Symbol Optimum 1 Optimum 2 • We construct a last component out of six copies of Component 1 • For the three points labeled A, B, C, there are two induced coalition structures given in Optimum 1 and Optimum 2, for which the contribution of the edge values in the component is maximal 50

Construct 1 • We combine the components of the 5 types in certain constructs • Construct 1 below is such that in any locally optimal coalition structure, nodes X and Y are always in the same coalition and the pair of nodes labeled A lie in the same coalition if and only if the pair of nodes labeled B lie in the same coalition Construction Optimum 1 Optimum 2 51

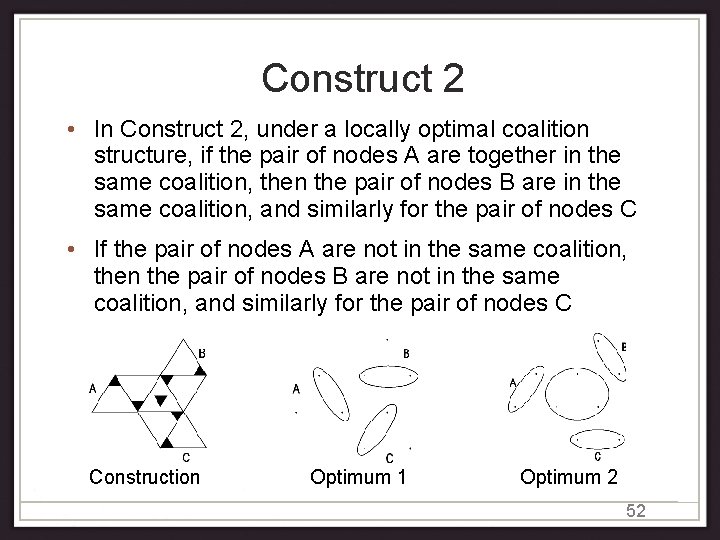
Construct 2 • In Construct 2, under a locally optimal coalition structure, if the pair of nodes A are together in the same coalition, then the pair of nodes B are in the same coalition, and similarly for the pair of nodes C • If the pair of nodes A are not in the same coalition, then the pair of nodes B are not in the same coalition, and similarly for the pair of nodes C Construction Optimum 1 Optimum 2 52

Construct 3 • Construct 3 is similar, except that the state of whether or not the pair of nodes C are in the same coalition as each other is the opposite to the state of whether or not the pair of nodes A are in the same coalition as each other Construction Optimum 1 Optimum 2 53

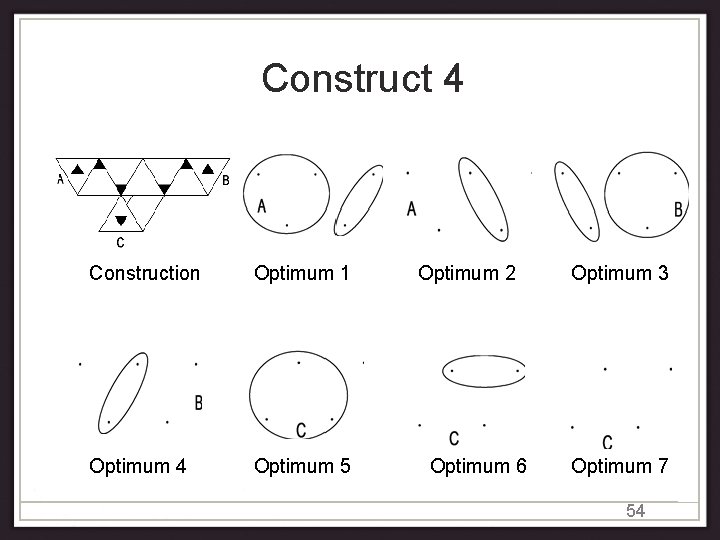
Construct 4 Construction Optimum 1 Optimum 4 Optimum 5 Optimum 2 Optimum 6 Optimum 3 Optimum 7 54

Graph construction • Create a copy of Construct 4 for each clause of the 3 SAT problem, where three pairs A, B, C are identified with the three literals in the corresponding clause • A coalition structure over these constructs is identified with a set of logical values for the literals in the clauses (the literal associated with a pair of node is set as true if and only if those nodes are not in the same coalition) • Use Component 4 to connect the pairs of nodes that represent literals of the same variable or its negation to a series of copies of Constructs 2 and 3 55

Graph construction • This allows us to ensure that any locally optimal coalition structure assigns consistent logical values to variables • To ensure that the resulting graph is planar, we can replace any pair of Components 4 which cross over with two copies of Construct 1 56

Finally, • A locally optimal coalition structure exists if and only if the original 3 -SAT problem is satisfiable, and given any locally optimal coalition structure, we can identify a solution to the 3 -SAT problem • If a locally optimal coalition structure exists, then a coalition structure is optimal iff it is locally optimal • The size of this graph is O(m 2) ☐ 58

Summary

We gave bounds on computation of the exact optimal coalition structure over general and minor free graphs with an IDM characteristic function. Proved polynomial time solvability for bounded treewidth graphs and NP-hardness for planar graphs. Future work: Efficient approximation algorithms are required. 60

Thanks!

Thanks!