Graph Algorithms Topological Sort The topological sorting problem

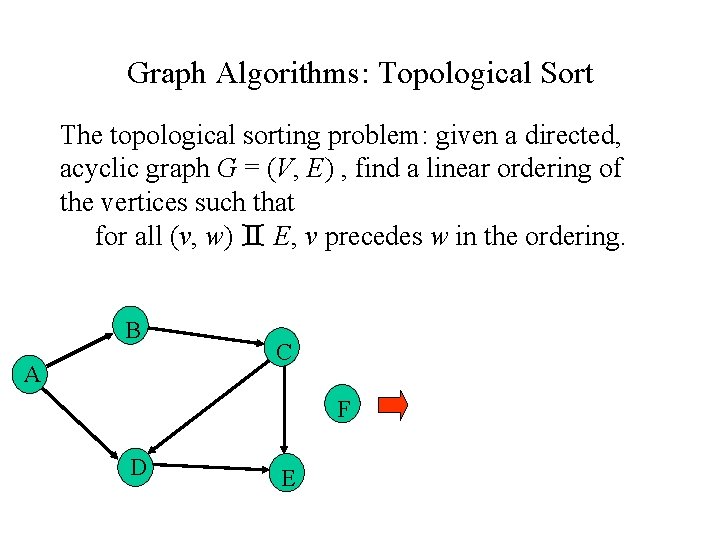
Graph Algorithms: Topological Sort The topological sorting problem: given a directed, acyclic graph G = (V, E) , find a linear ordering of the vertices such that for all (v, w) E, v precedes w in the ordering. B A C F D E

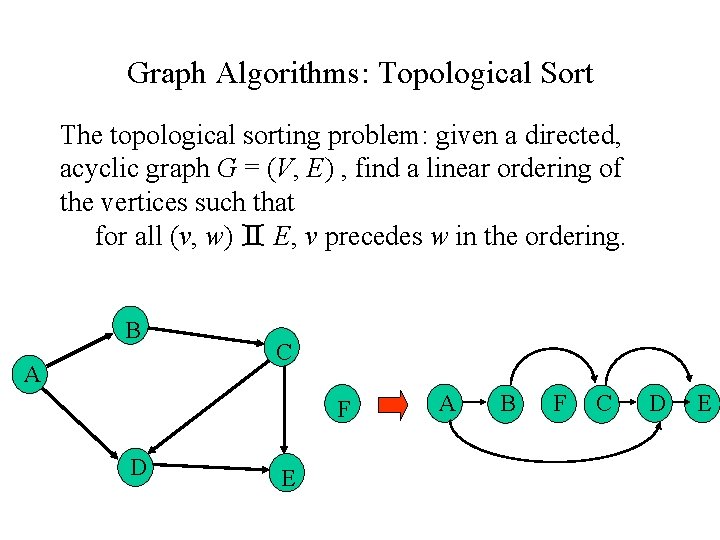
Graph Algorithms: Topological Sort The topological sorting problem: given a directed, acyclic graph G = (V, E) , find a linear ordering of the vertices such that for all (v, w) E, v precedes w in the ordering. B A C F D E A B F C D E

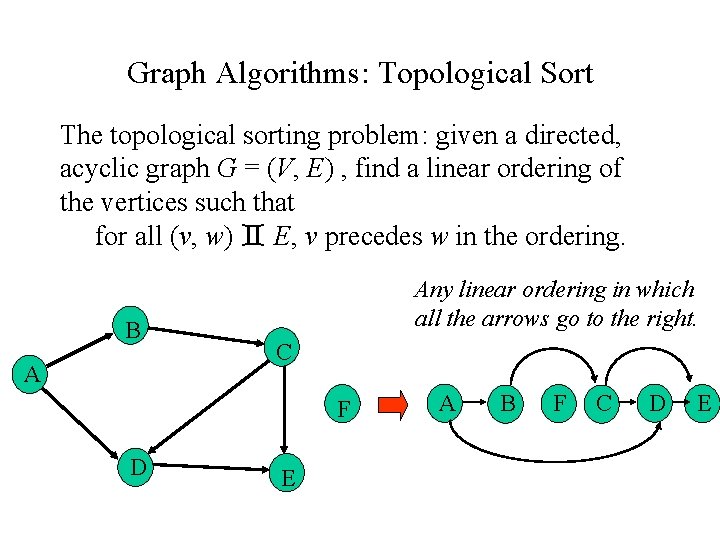
Graph Algorithms: Topological Sort The topological sorting problem: given a directed, acyclic graph G = (V, E) , find a linear ordering of the vertices such that for all (v, w) E, v precedes w in the ordering. B A Any linear ordering in which all the arrows go to the right. C F D E A B F C D E

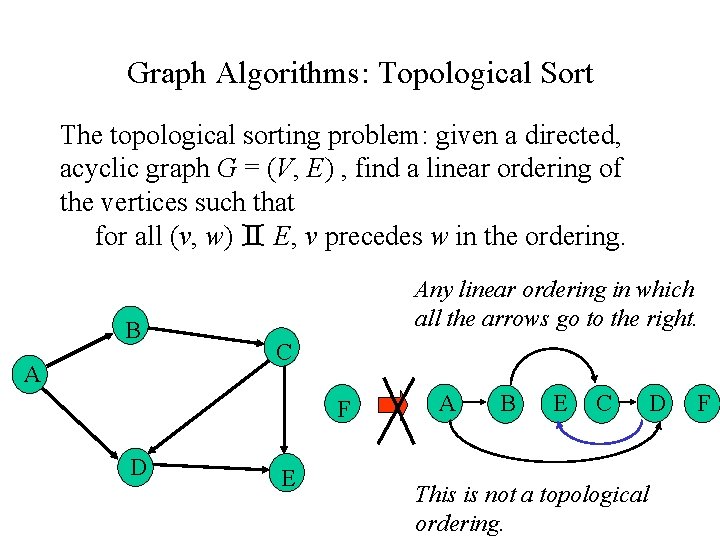
Graph Algorithms: Topological Sort The topological sorting problem: given a directed, acyclic graph G = (V, E) , find a linear ordering of the vertices such that for all (v, w) E, v precedes w in the ordering. B A Any linear ordering in which all the arrows go to the right. C F D E A B E C This is not a topological ordering. D F

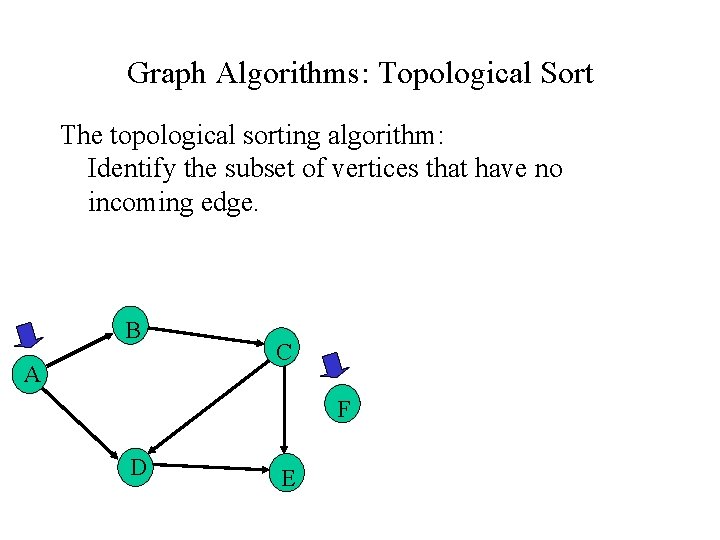
Graph Algorithms: Topological Sort The topological sorting algorithm: Identify the subset of vertices that have no incoming edge. B A C F D E

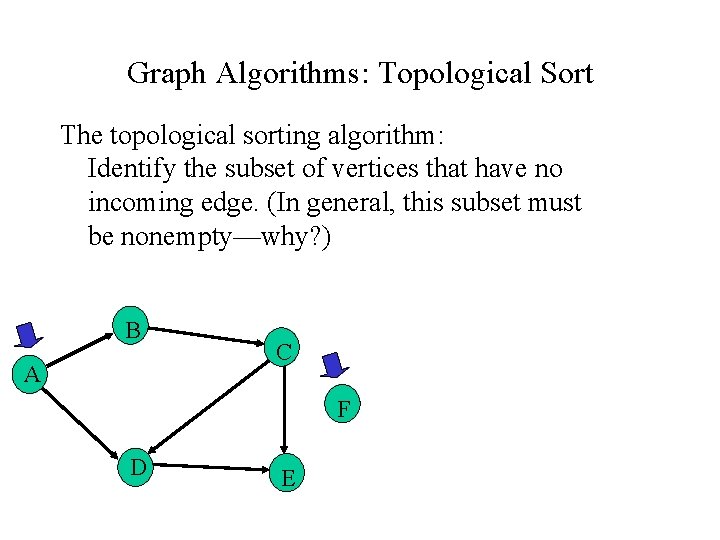
Graph Algorithms: Topological Sort The topological sorting algorithm: Identify the subset of vertices that have no incoming edge. (In general, this subset must be nonempty—why? ) B A C F D E

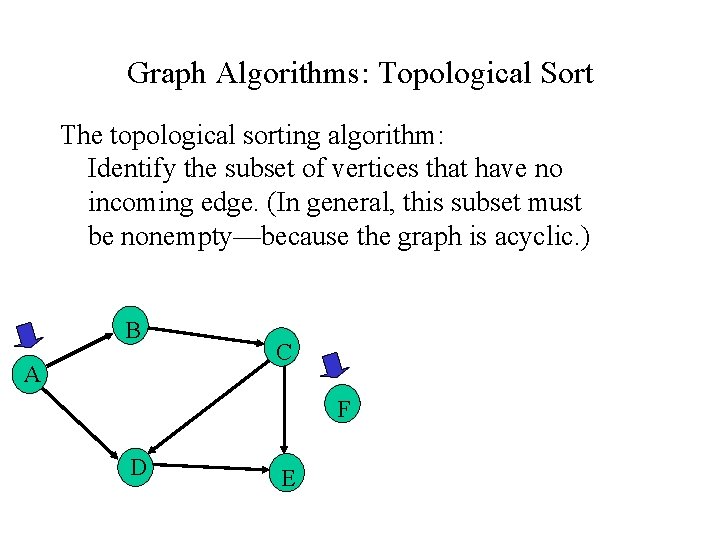
Graph Algorithms: Topological Sort The topological sorting algorithm: Identify the subset of vertices that have no incoming edge. (In general, this subset must be nonempty—because the graph is acyclic. ) B A C F D E

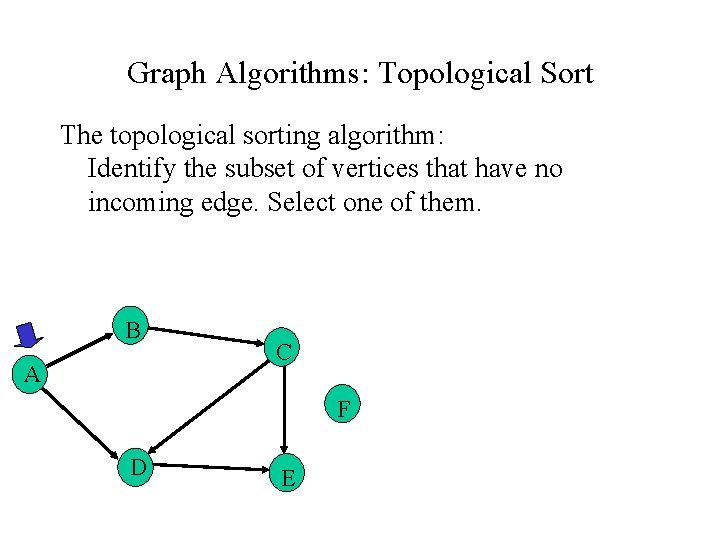
Graph Algorithms: Topological Sort The topological sorting algorithm: Identify the subset of vertices that have no incoming edge. Select one of them. B A C F D E

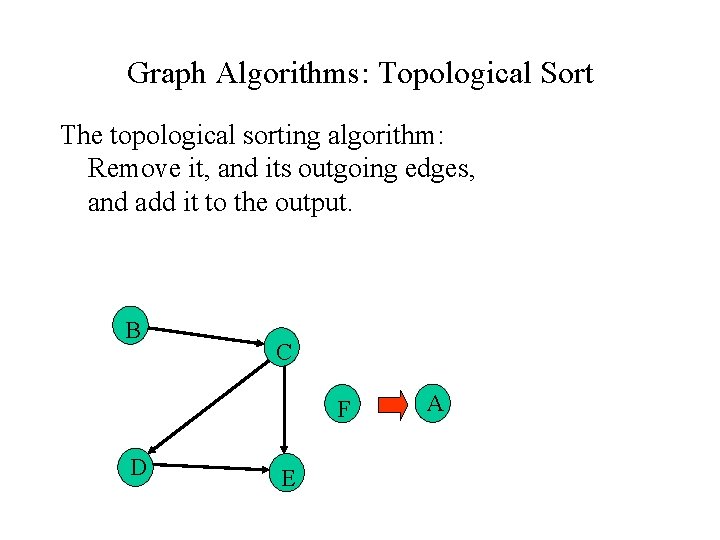
Graph Algorithms: Topological Sort The topological sorting algorithm: Remove it, and its outgoing edges, and add it to the output. B C F D E A

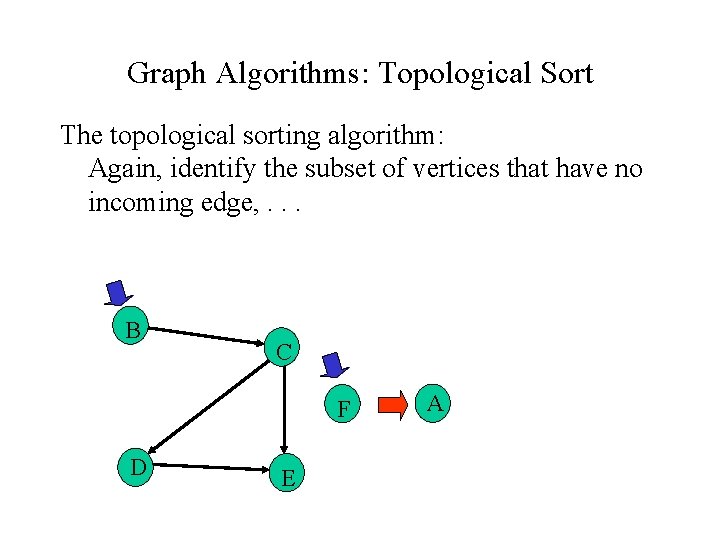
Graph Algorithms: Topological Sort The topological sorting algorithm: Again, identify the subset of vertices that have no incoming edge, . . . B C F D E A

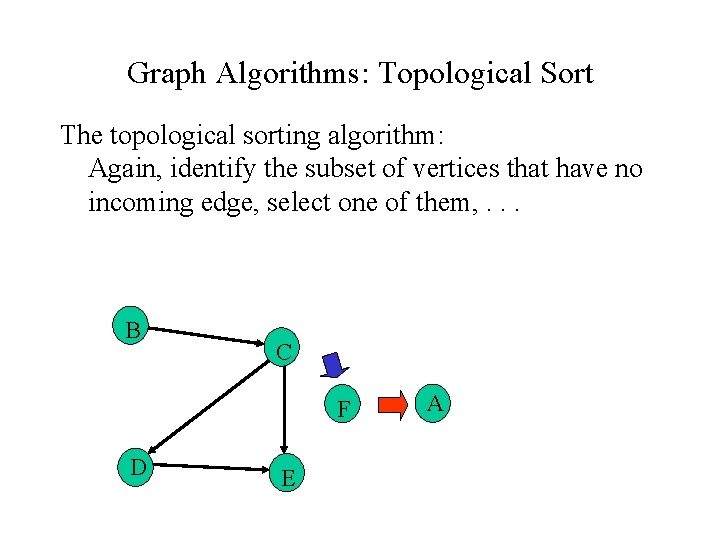
Graph Algorithms: Topological Sort The topological sorting algorithm: Again, identify the subset of vertices that have no incoming edge, select one of them, . . . B C F D E A

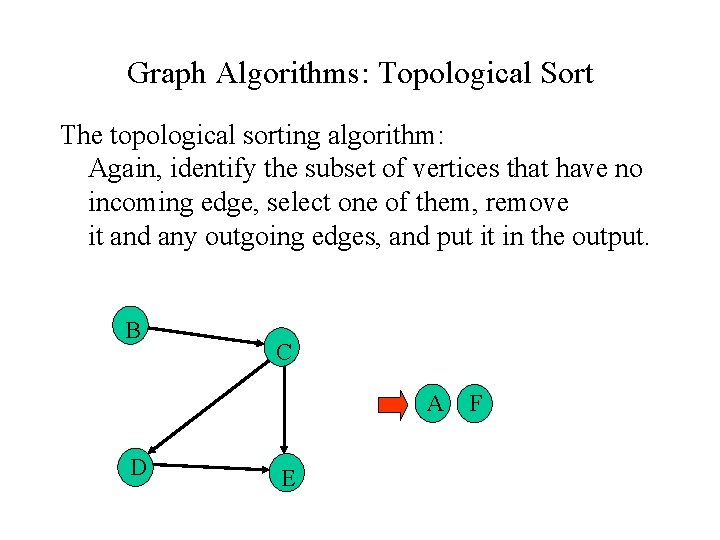
Graph Algorithms: Topological Sort The topological sorting algorithm: Again, identify the subset of vertices that have no incoming edge, select one of them, remove it and any outgoing edges, and put it in the output. B C A D E F

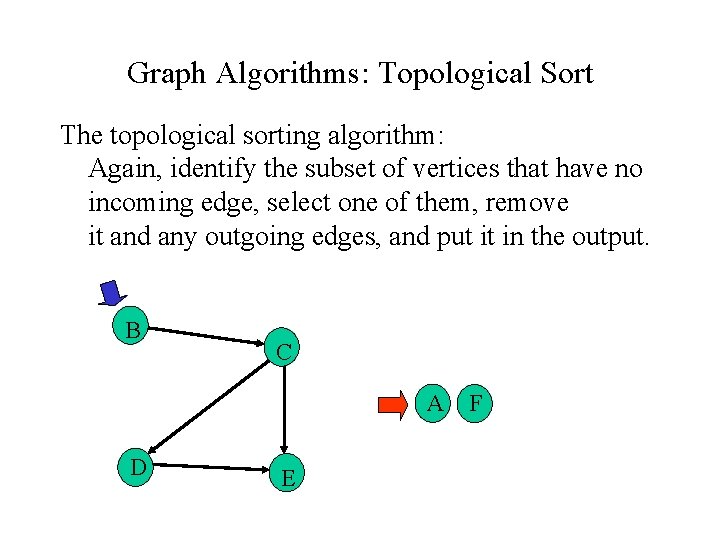
Graph Algorithms: Topological Sort The topological sorting algorithm: Again, identify the subset of vertices that have no incoming edge, select one of them, remove it and any outgoing edges, and put it in the output. C A D E F B

Graph Algorithms: Topological Sort The topological sorting algorithm: Again, identify the subset of vertices that have no incoming edge, select one of them, remove it and any outgoing edges, and put it in the output. A D E F B C

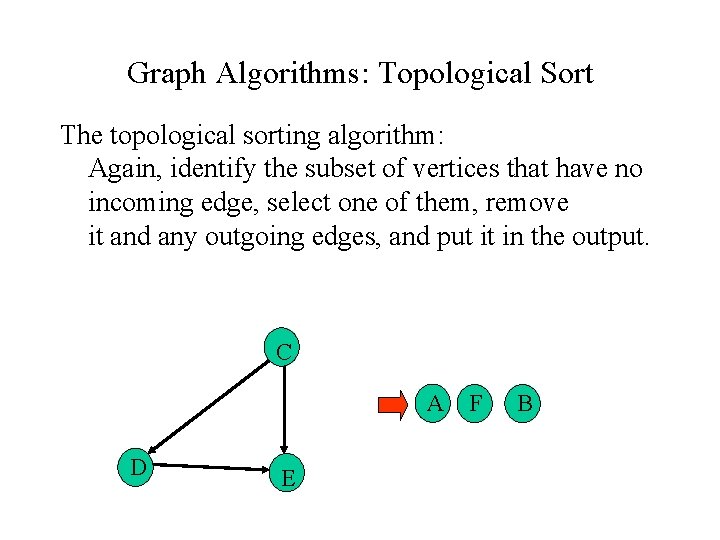
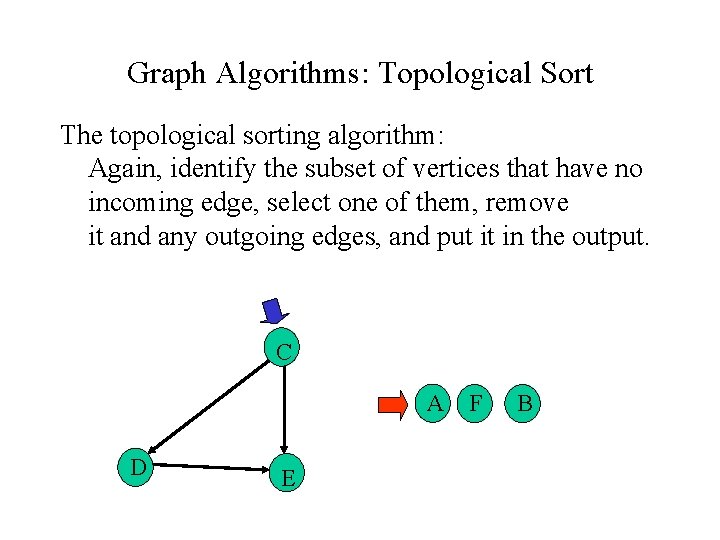
Graph Algorithms: Topological Sort The topological sorting algorithm: Again, identify the subset of vertices that have no incoming edge, select one of them, remove it and any outgoing edges, and put it in the output. A E F B C D

Graph Algorithms: Topological Sort The topological sorting algorithm: Again, identify the subset of vertices that have no incoming edge, select one of them, remove it and any outgoing edges, and put it in the output. A F B C D E

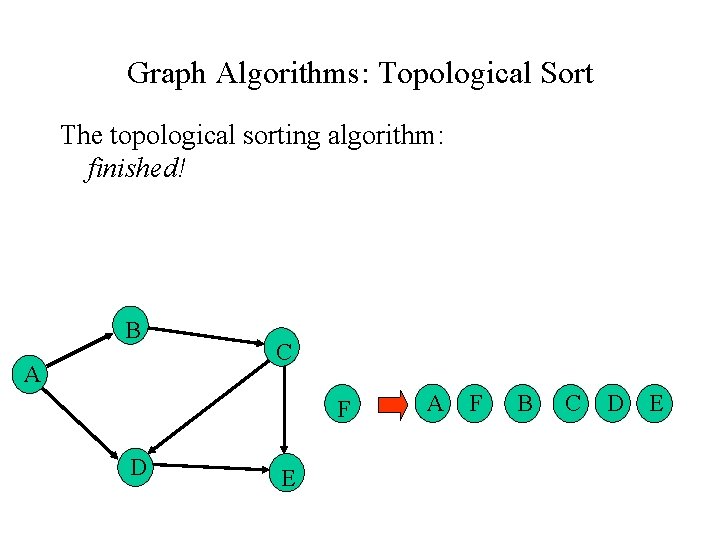
Graph Algorithms: Topological Sort The topological sorting algorithm: finished! B A C F D E A F B C D E

Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound? B A C F D E A F B C D E

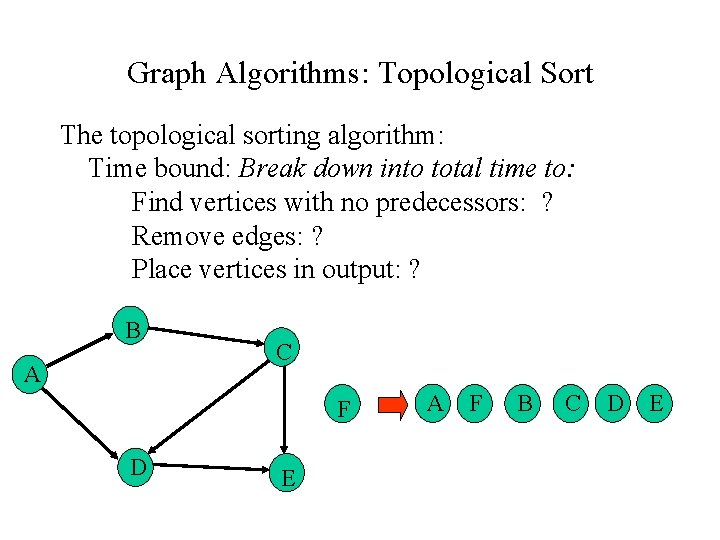
Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound: Break down into total time to: Find vertices with no predecessors: ? Remove edges: ? Place vertices in output: ? B A C F D E A F B C D E

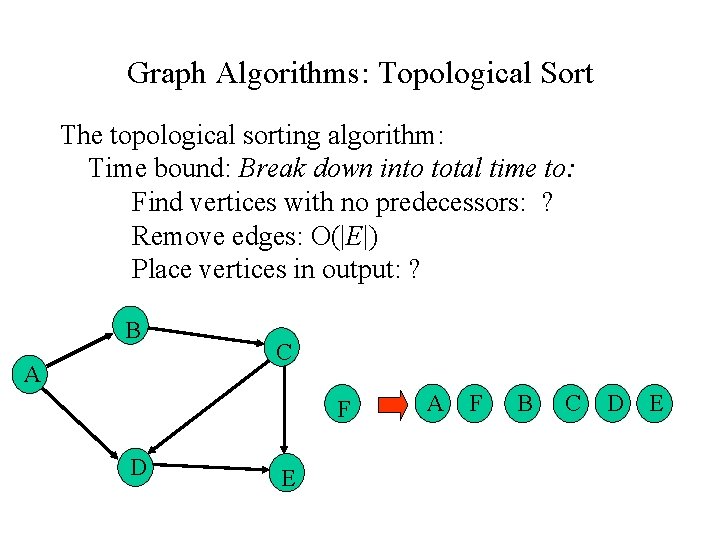
Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound: Break down into total time to: Find vertices with no predecessors: ? Remove edges: O(|E|) Place vertices in output: ? B A C F D E A F B C D E

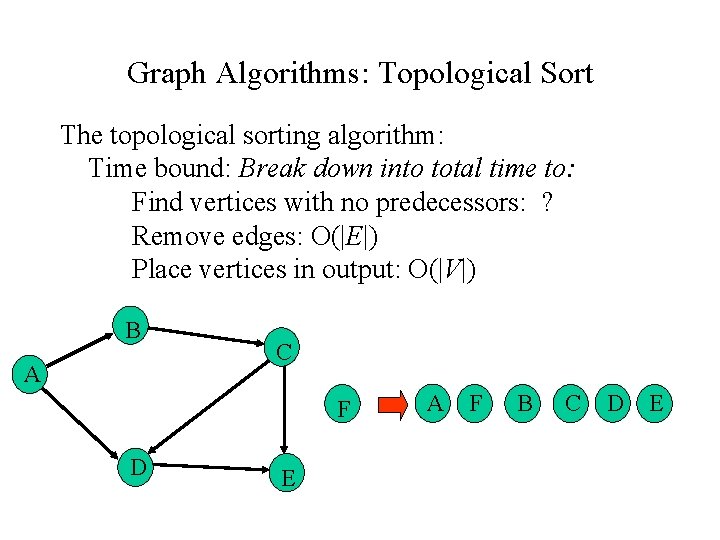
Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound: Break down into total time to: Find vertices with no predecessors: ? Remove edges: O(|E|) Place vertices in output: O(|V|) B A C F D E A F B C D E

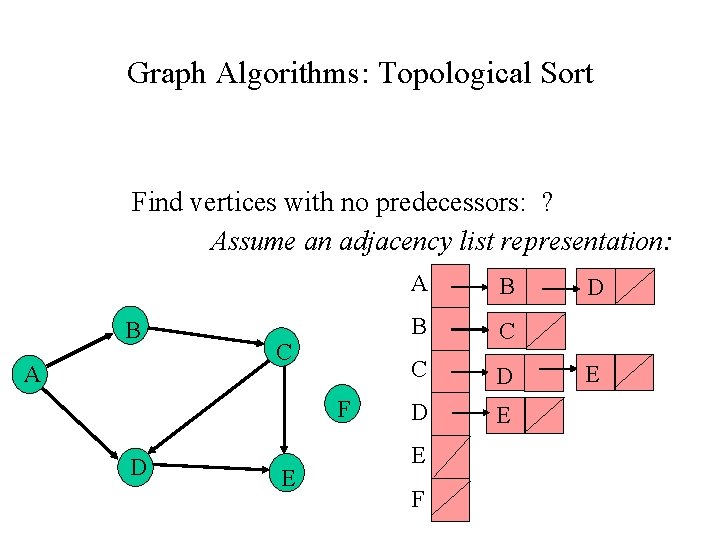
Graph Algorithms: Topological Sort Find vertices with no predecessors: ? Assume an adjacency list representation: B A C F D E A B B C C D D E E F D E

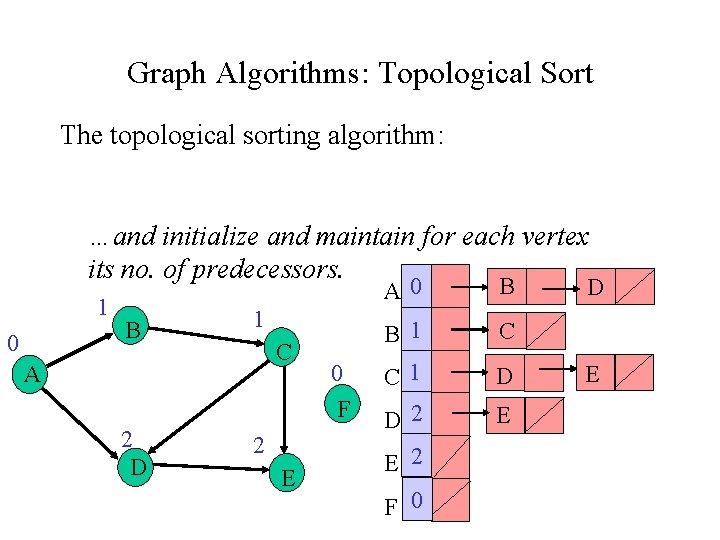
Graph Algorithms: Topological Sort The topological sorting algorithm: …and initialize and maintain for each vertex its no. of predecessors. 1 0 B 1 C A 2 D 2 E 0 F A 0 B B 1 C C 1 D 2 D E 2 F 0 E D E

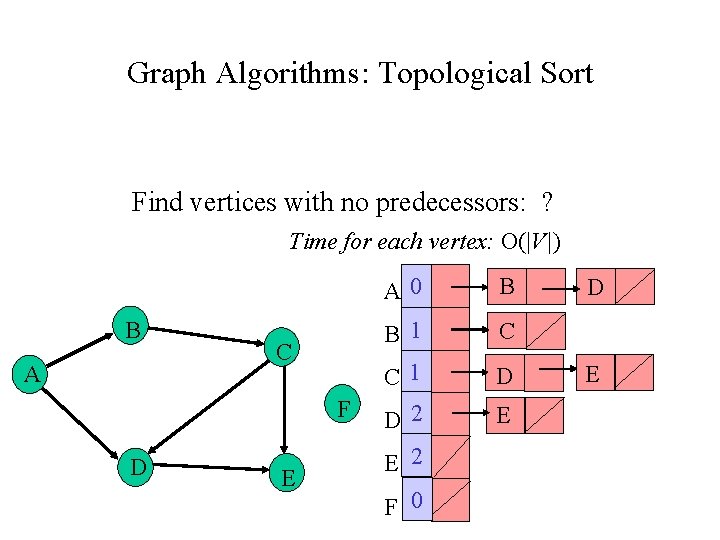
Graph Algorithms: Topological Sort Find vertices with no predecessors: ? Time for each vertex: O(|V|) B A C F D E A 0 B B 1 C C 1 D 2 D E 2 F 0 E D E

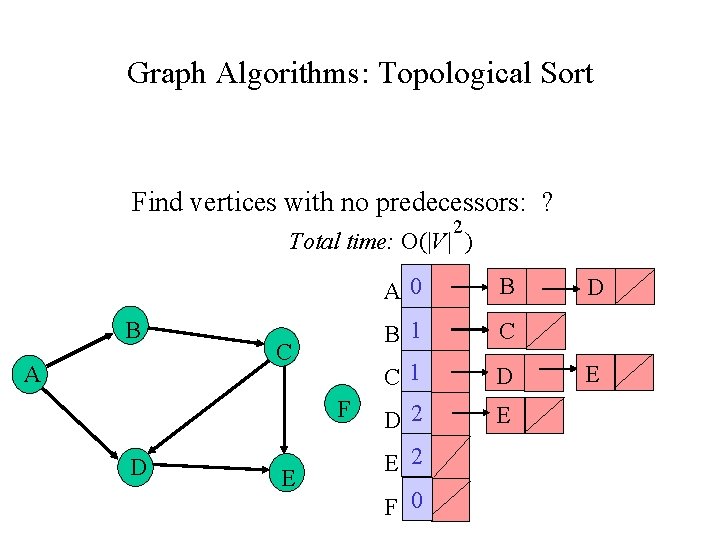
Graph Algorithms: Topological Sort Find vertices with no predecessors: ? 2 Total time: O(|V| ) B A C F D E A 0 B B 1 C C 1 D 2 D E 2 F 0 E D E

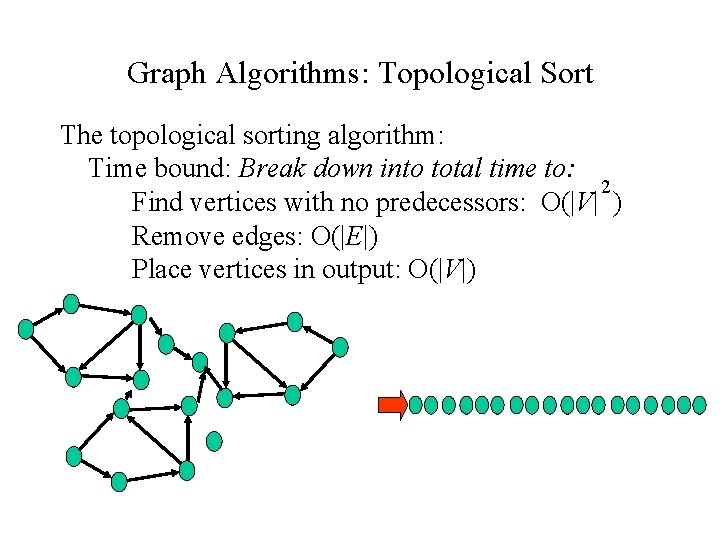
Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound: Break down into total time to: 2 Find vertices with no predecessors: O(|V| ) Remove edges: O(|E|) Place vertices in output: O(|V|)

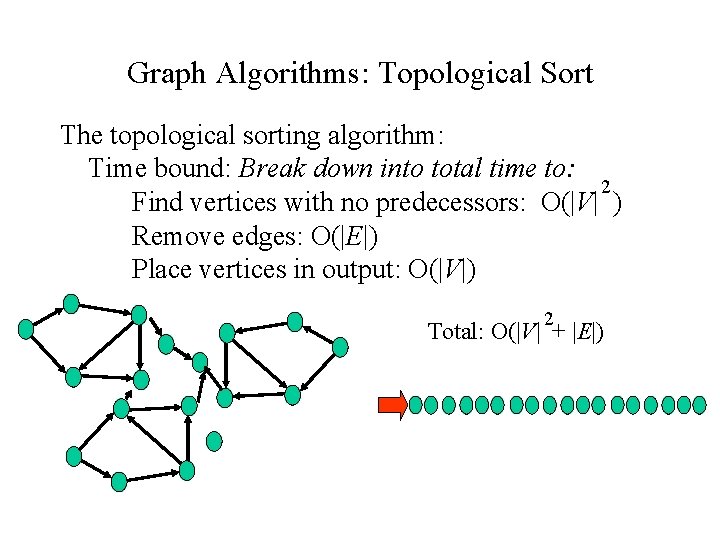
Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound: Break down into total time to: 2 Find vertices with no predecessors: O(|V| ) Remove edges: O(|E|) Place vertices in output: O(|V|) 2 Total: O(|V| + |E|)

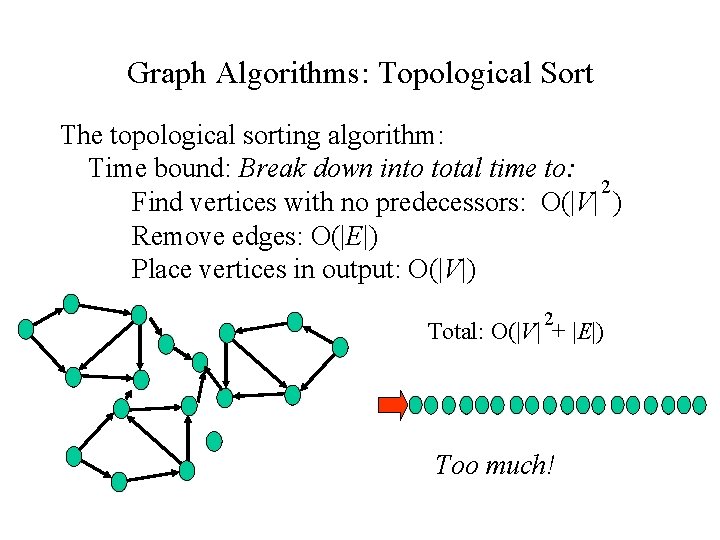
Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound: Break down into total time to: 2 Find vertices with no predecessors: O(|V| ) Remove edges: O(|E|) Place vertices in output: O(|V|) 2 Total: O(|V| + |E|) Too much!

Graph Algorithms: Topological Sort The topological sorting algorithm: We need a faster way to do this step: Find vertices with no predecessors.

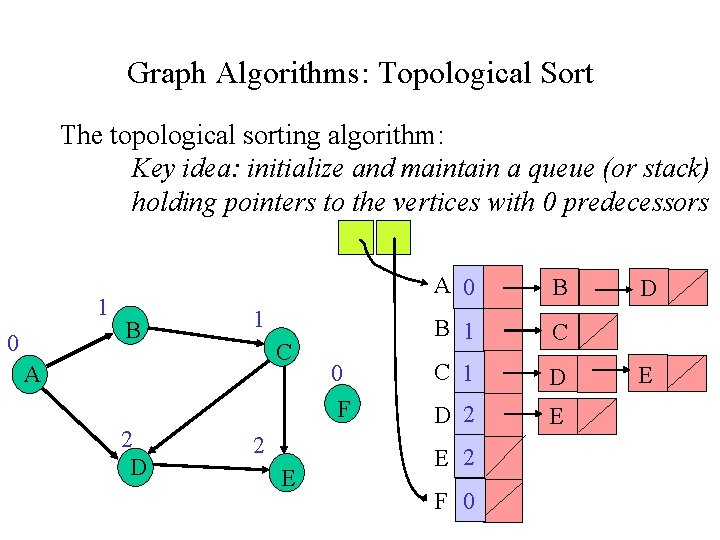
Graph Algorithms: Topological Sort The topological sorting algorithm: Key idea: initialize and maintain a queue (or stack) holding pointers to the vertices with 0 predecessors 1 0 B 1 C A 2 D 2 E 0 F A 0 B B 1 C C 1 D D 2 E E 2 F 0 D E

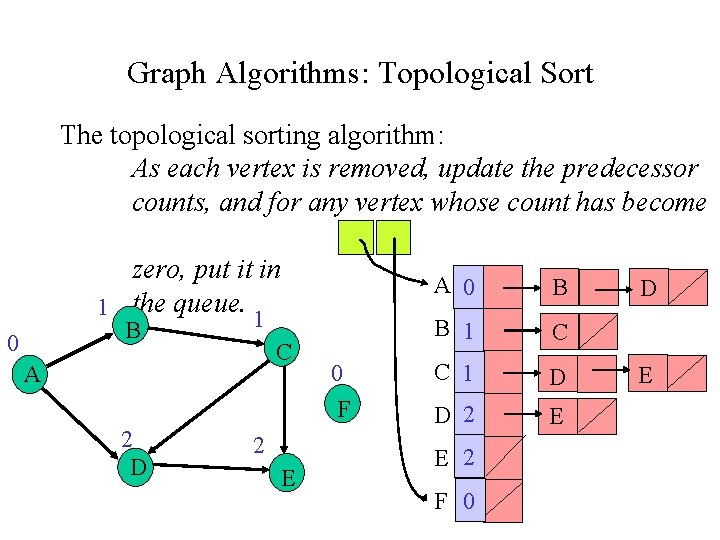
Graph Algorithms: Topological Sort The topological sorting algorithm: As each vertex is removed, update the predecessor counts, and for any vertex whose count has become zero, put it in 1 the queue. 1 B 0 C A 2 D 2 E 0 F A 0 B B 1 C C 1 D D 2 E E 2 F 0 D E

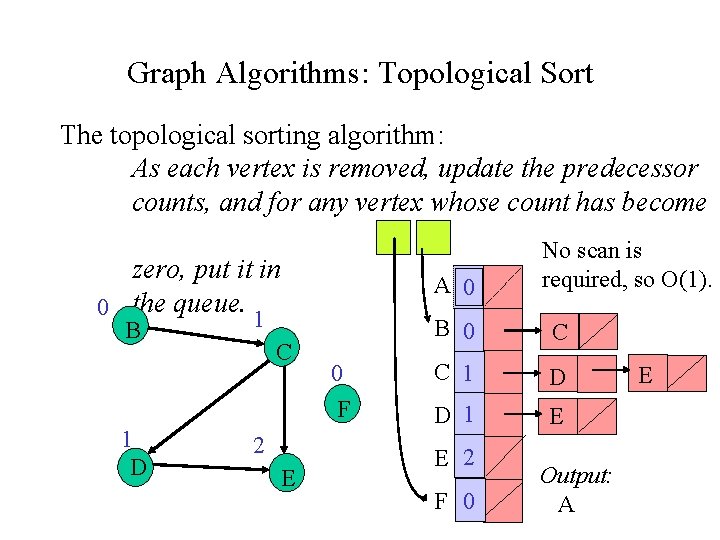
Graph Algorithms: Topological Sort The topological sorting algorithm: As each vertex is removed, update the predecessor counts, and for any vertex whose count has become zero, put it in 0 the queue. 1 B 1 D A 0 C 2 E 0 F No scan is required, so O(1). B 0 C C 1 D D 1 E E 2 F 0 Output: A E

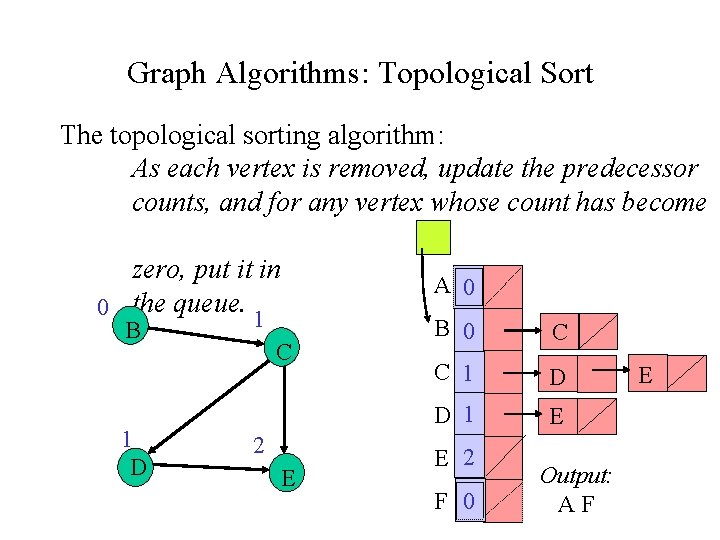
Graph Algorithms: Topological Sort The topological sorting algorithm: As each vertex is removed, update the predecessor counts, and for any vertex whose count has become zero, put it in 0 the queue. 1 B 1 D A 0 C 2 E B 0 C C 1 D D 1 E E 2 F 0 Output: AF E

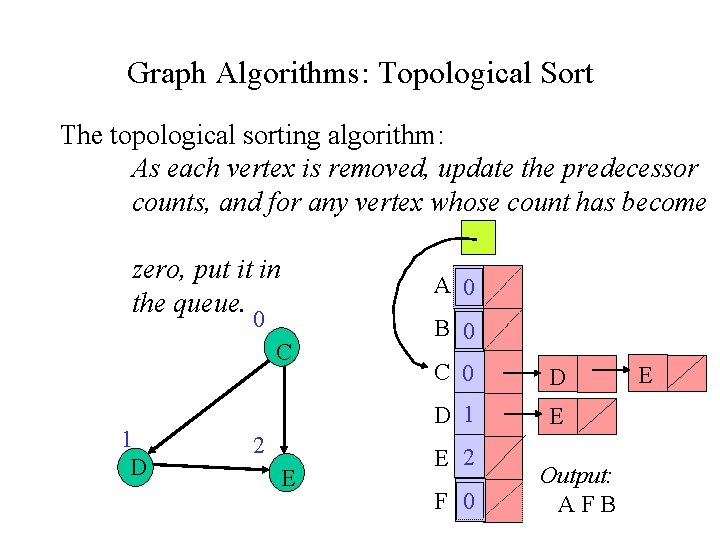
Graph Algorithms: Topological Sort The topological sorting algorithm: As each vertex is removed, update the predecessor counts, and for any vertex whose count has become zero, put it in the queue. A 0 0 C 1 D 2 E B 0 C 0 D D 1 E E 2 F 0 Output: AFB E

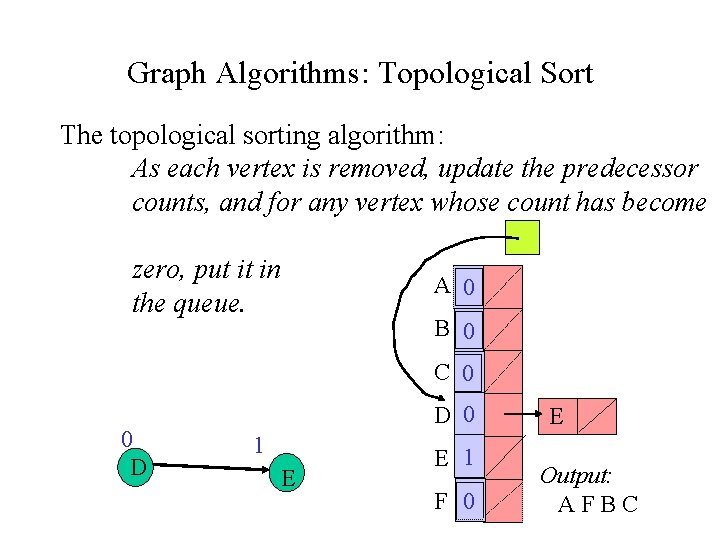
Graph Algorithms: Topological Sort The topological sorting algorithm: As each vertex is removed, update the predecessor counts, and for any vertex whose count has become zero, put it in the queue. A 0 B 0 C 0 0 D D 0 1 E E 1 F 0 E Output: AFBC

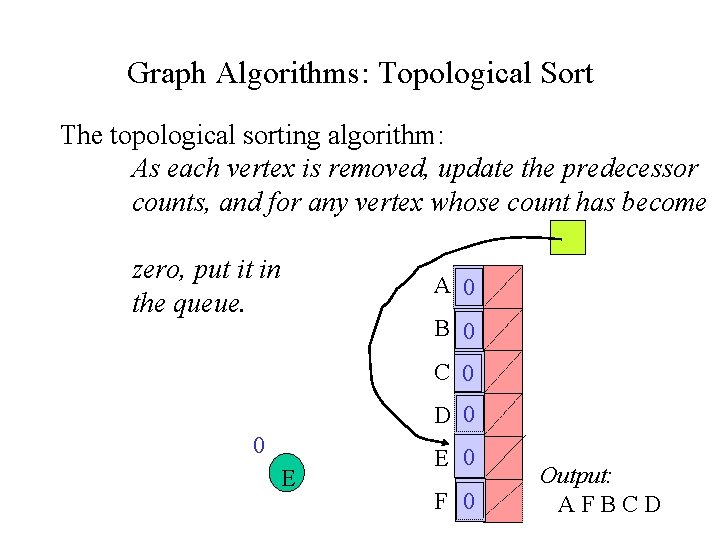
Graph Algorithms: Topological Sort The topological sorting algorithm: As each vertex is removed, update the predecessor counts, and for any vertex whose count has become zero, put it in the queue. A 0 B 0 C 0 D 0 0 E E 0 F 0 Output: AFBCD

Graph Algorithms: Topological Sort The topological sorting algorithm: As each vertex is removed, update the predecessor counts, and for any vertex whose count has become zero, put it in the queue. A 0 Finished! C 0 B 0 D 0 E 0 F 0 Output: AFBCDE

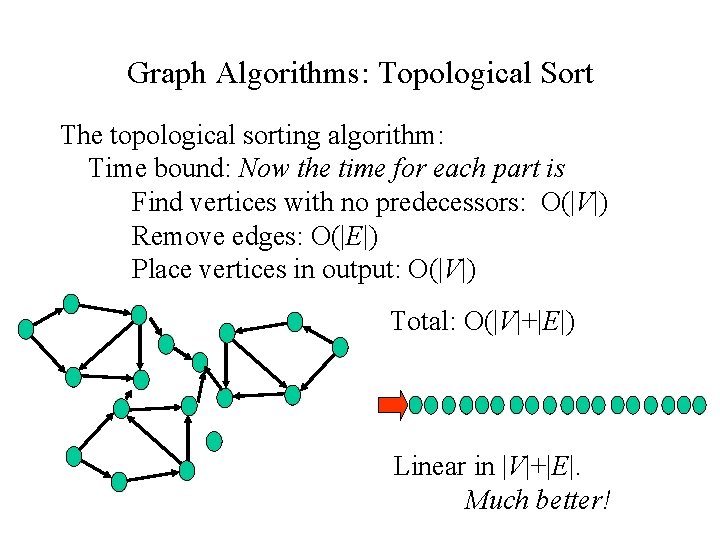
Graph Algorithms: Topological Sort The topological sorting algorithm: Time bound: Now the time for each part is Find vertices with no predecessors: O(|V|) Remove edges: O(|E|) Place vertices in output: O(|V|) Total: O(|V|+|E|) Linear in |V|+|E|. Much better!