Graph Algorithms Minimum Spanning Trees MST Union Find

Graph Algorithms Minimum Spanning Trees (MST) Union - Find Dana Shapira 1

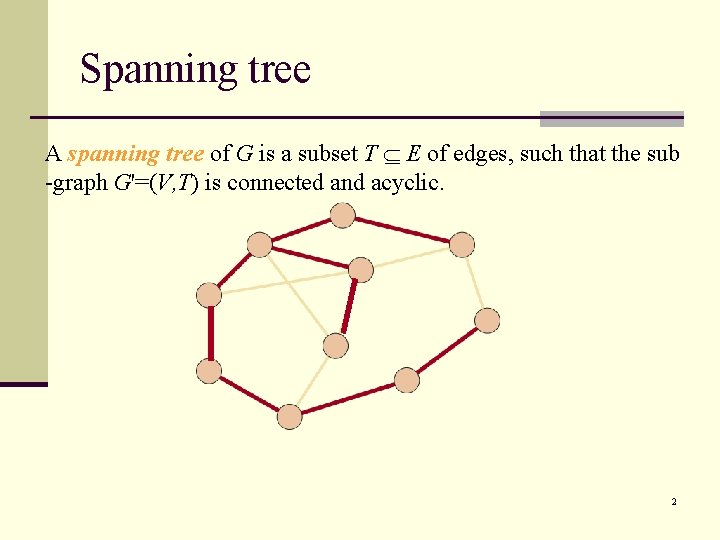
Spanning tree A spanning tree of G is a subset T E of edges, such that the sub -graph G'=(V, T) is connected and acyclic. 2

Minimum Spanning Tree Given a graph G = (V, E) and an assignment of weights w(e) to the edges of G, a minimum spanning tree T of G is a spanning tree with minimum total edge weight 1 3 3 6 6 9 7 8 1 3 2 7 5 4 3

How To Build A Minimum Spanning Tree n General strategy: 1. Maintain a set of edges A such that (V, A) is a spanning forest of G and such that there exists a MST (V, F) of G such that A F. 2. As long as (V, A) is not a tree, find an edge that can be added to A while maintaining the above property. Generic-MST(G=(V, E)) 1. A= ; 2. while (A is not a spanning tree of G) do 3. choose a safe edge e=(u, v) E 4. A=A {e} 5. return A 4

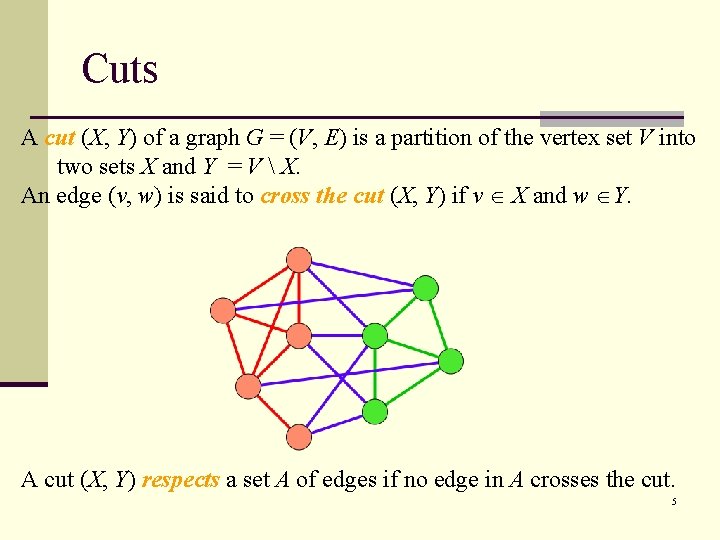
Cuts A cut (X, Y) of a graph G = (V, E) is a partition of the vertex set V into two sets X and Y = V X. An edge (v, w) is said to cross the cut (X, Y) if v X and w Y. A cut (X, Y) respects a set A of edges if no edge in A crosses the cut. 5

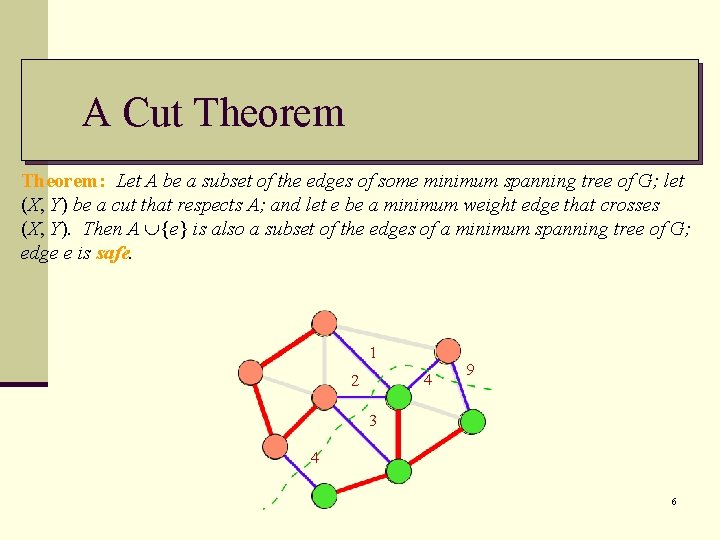
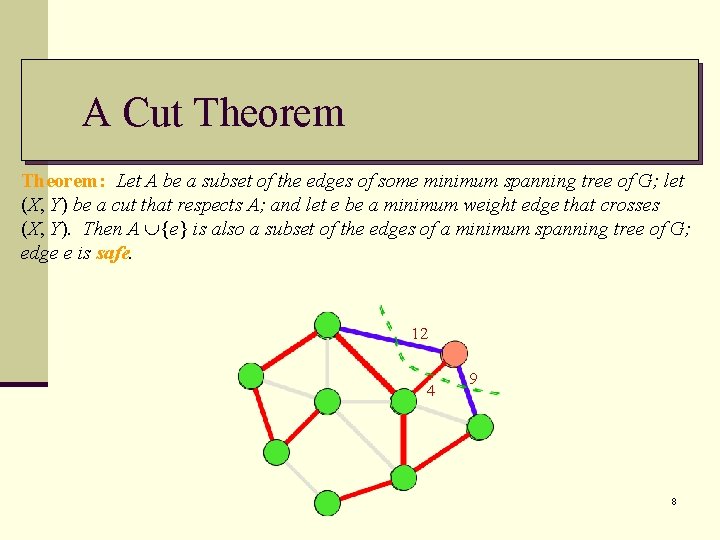
A Cut Theorem: Let A be a subset of the edges of some minimum spanning tree of G; let (X, Y) be a cut that respects A; and let e be a minimum weight edge that crosses (X, Y). Then A {e} is also a subset of the edges of a minimum spanning tree of G; edge e is safe. 1 4 2 9 3 4 6

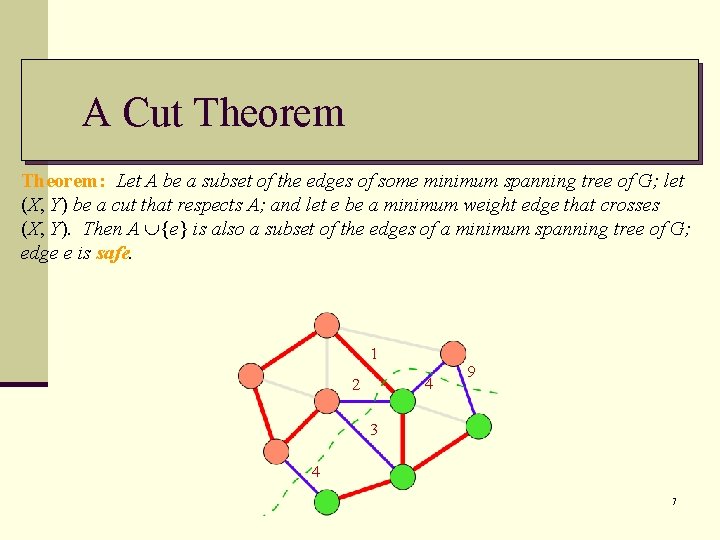
A Cut Theorem: Let A be a subset of the edges of some minimum spanning tree of G; let (X, Y) be a cut that respects A; and let e be a minimum weight edge that crosses (X, Y). Then A {e} is also a subset of the edges of a minimum spanning tree of G; edge e is safe. 1 4 2 9 3 4 7

A Cut Theorem: Let A be a subset of the edges of some minimum spanning tree of G; let (X, Y) be a cut that respects A; and let e be a minimum weight edge that crosses (X, Y). Then A {e} is also a subset of the edges of a minimum spanning tree of G; edge e is safe. 12 4 9 8

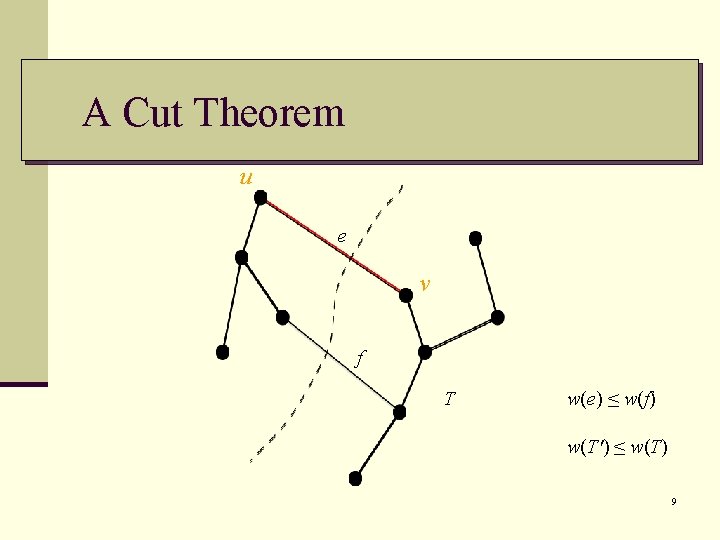
A Cut Theorem u e v f T w(e) ≤ w(f) w(T') ≤ w(T) 9

Proof: n Let T be a MST such that A T. n If e = (u, v) T, add e to T. n The edge e = (u, v) forms a cycle with edges on the path p from u to v in T. Since u and v are on opposite sides of the cut, there is at least one edge f = (x, y) in T on the path p that also crosses the cut. n f A since the cut respects A. Since f is on the unique path from u to v in T, removing it breaks T into two components. n w(e) ≤ w(f) (why? ) n Let T ' = T – {f} {e} w(T ') ≤ w(T). 10

A Cut Theorem Corollary: Let G=(V, E) be a connected undirected graph and A a subset of E included in a minimum spanning tree T for G, and let C=(VC, EC) be a tree in the forest GA=(V, A). If e is a light edge connecting C to some other component in GA, then e is safe for A. Proof: The cut (VC, V–VC) respects A, and e is a light edge for this cut. Therefore, e is safe. 11

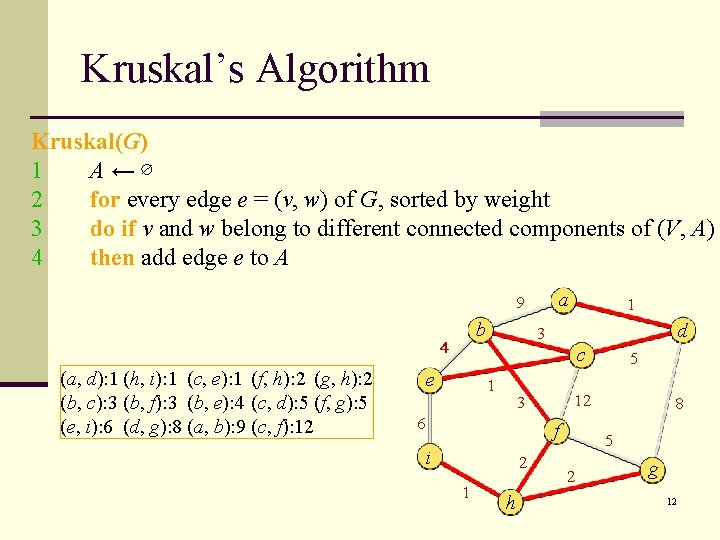
Kruskal’s Algorithm Kruskal(G) 1 A←∅ 2 for every edge e = (v, w) of G, sorted by weight 3 do if v and w belong to different connected components of (V, A) 4 then add edge e to A a 9 b 4 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 1 d 3 c e 1 12 3 6 f i 2 1 h 5 8 5 2 g 12

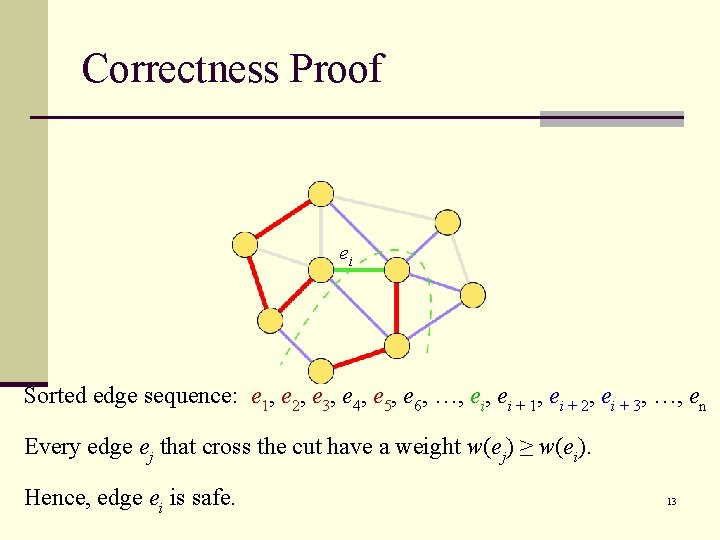
Correctness Proof ei Sorted edge sequence: e 1, e 2, e 3, e 4, e 5, e 6, …, ei + 1, ei + 2, ei + 3, …, en Every edge ej that cross the cut have a weight w(ej) ≥ w(ei). Hence, edge ei is safe. 13

Union-Find Data Structures n. Given a set S of n elements, maintain a partition of S into subsets S 1, S 2, …, Sk n. Support the following operations: n. Union(x, y): Replace sets Si and Sj such that x Si and y Sj with Si Sj in the current partition n. Find(x): Returns a member r(Si) of the set Si that contains x n. In particular, Find(x) and Find(y) return the same element if and only if x and y belong to the same set. n. It is possible to create a data structure that supports the above operations in O(α(n)) amortized time, where α is the inverse Ackermann function. 14

Kruskal’s Algorithm Using Union. Find Data Structure Kruskal(G, w) A for each vertex v V do Make-Set(v) sort the edges in E in non-decreasing weight order w for each edge (u, v) E do if Find-Set(u) ≠ Find-Set(v) then A A {(u, v)} Union(u, v) return A 15

Kruskal’s Algorithm Using Union. Find Data Structure n. Analysis: n. O(|E| log |E|) time for everything except the operations on S n. Cost of operations on S: n. O(α(|E|, |V|)) amortized time per operation on S n|V| – 1 Union operations n|E| Find operations n. Total: O((|V| + |E|)α(|E|, |V|)) running time n. Total running time: O(|E| lg |E|). 16

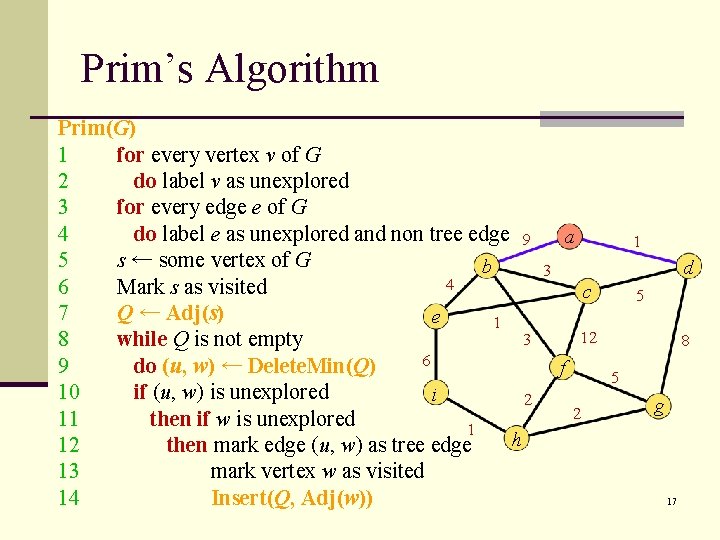
Prim’s Algorithm Prim(G) 1 for every vertex v of G 2 do label v as unexplored 3 for every edge e of G 4 do label e as unexplored and non tree edge 9 5 s ← some vertex of G b 4 6 Mark s as visited 7 Q ← Adj(s) e 1 3 8 while Q is not empty 6 9 do (u, w) ← Delete. Min(Q) 10 if (u, w) is unexplored i 2 11 then if w is unexplored 1 h 12 then mark edge (u, w) as tree edge 13 mark vertex w as visited 14 Insert(Q, Adj(w)) a 1 d 3 c 5 12 f 8 5 2 g 17

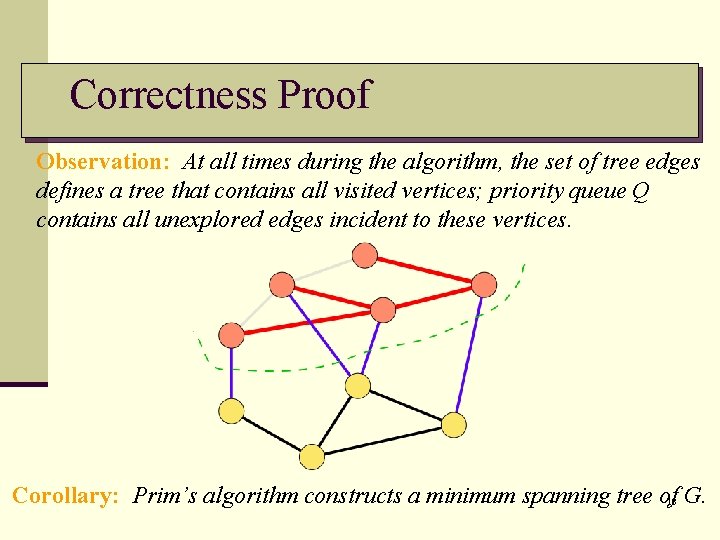
Correctness Proof Observation: At all times during the algorithm, the set of tree edges defines a tree that contains all visited vertices; priority queue Q contains all unexplored edges incident to these vertices. Corollary: Prim’s algorithm constructs a minimum spanning tree of 18 G.

Union/Find n Assumptions: The Sets are disjoint. n Each set is identified by a representative of the set. n Initial state: n A union/find structure begins with n elements, each considered to be a one element set. n Functions: n Make-Set(x): Creates a new set with element x in it. n Union(x, y): Make one set out of the sets containing x and y. n Find-Set(x): Returns a pointer to the representative of the set containing x. n 19

Basic Notation n The elements in the structure will be numbered 0 to n-1 n Each set will be referred to by the number of one of the element it contains n Initially we have sets S 0, S 1, …, Sn-1 n If we were to call Union(S 2, S 4), these sets would be removed from the list, and the new set would now be called either S 2 or S 4 n Notations: n n Make-Set operations n m total operations n n m 20

First Attempt n n Represent the Union/Find structure as an array arr of n elements arr[i] contains the set number of element i n Initially, arr[i]=i (Make-Set(i)) Find-Set(i) just returns the value of arr[i] To perform Union(Si, Sj): n For every k such that arr[k]=j, set arr[k]=i 21

Analysis n The worst-case analysis: n n Find(i) takes O(1) time Union(Si, Sj) takes (n) time n A sequence of n Unions will take (n 2) time 22

Second Attempt n Represent the Union/Find structure using linked lists. n Each element points to another element of the set. n The representative is the first element of the set. n Each element points to the representative. n How do we perform Union(Si, Sj)? 23

Analysis n The worst-case analysis: n n n Find(i) takes O(1) time Make-Set(i) takes O(1) time Union(Si, Sj) takes (n) time (Why? ) n A sequence of n Unions-Find will take (n 2) time (Example? ) 24

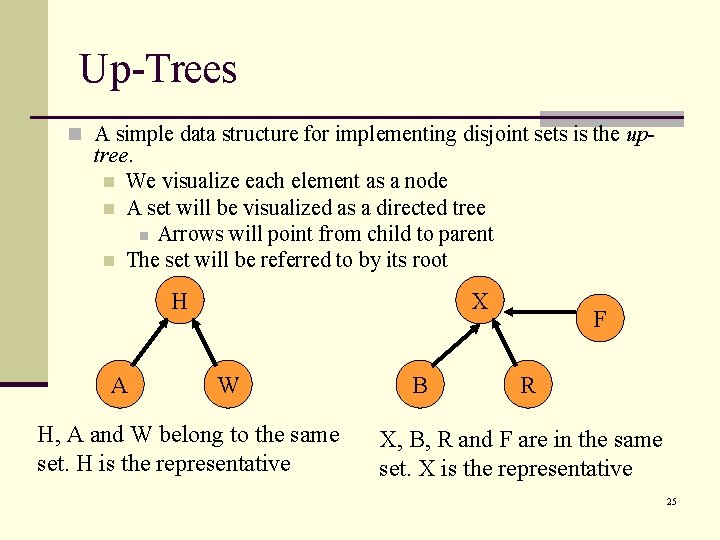
Up-Trees n A simple data structure for implementing disjoint sets is the up- tree. n We visualize each element as a node n A set will be visualized as a directed tree n Arrows will point from child to parent n The set will be referred to by its root H A X W H, A and W belong to the same set. H is the representative B F R X, B, R and F are in the same set. X is the representative 25

Operations in Up-Trees Follow pointer to representative element. find(x) { if (x≠p(x)) // not the representative then p(x) find(p(x)); return p(x); } 26

Union n Union is more complicated. n Make one representative element point to the other, but which way? Does it matter? 27

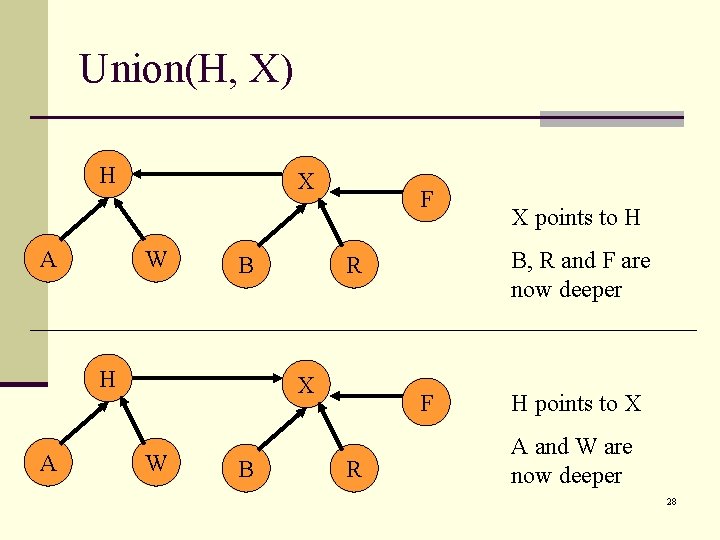
Union(H, X) H A X W B H A F W B B, R and F are now deeper R X F R X points to H H points to X A and W are now deeper 28

A worst case for Union can be done in O(1), but may cause find to become O(n) A B C D E Consider the result of the following sequence of operations: Union (A, B) Union (C, A) Union (D, C) Union (E, D) 29

Array Representation of Up-tree n Assume each element is associated with an integer i=0…n-1. From now on, we deal only with i. n Create an integer array, A[n] n An array entry is the element’s parent n A -1 entry signifies that element i is the representative element. 30

Array Representation of Up-tree Now the union algorithm might be: Union(x, y) { A[y] = x; // attaches y to x } The find algorithm would be find(x) { if (A[x] < 0) return(x); else return(find(A[x])); } Performance: ? ? ? 31

Analysis n Worst case: Union(Si, Sj) take O(1) time n Find(i) takes O(n) time n Can we do better in an amortized analysis? n What is the maximum amount of time n operations could take us? n Suppose we perform n/2 unions followed by n/2 finds n The n/2 unions could give us one tree of height n/2 -1 2 n Thus the total time would be n/2 + (n/2) = O(n ) n This strategy doesn’t really help… n 32

Array Representation of Up-tree n There are two heuristics that improve the performance of union-find. Union by weight n Path compression on find n 33

Union by Weight Heuristic Make-Set(x) { p(x) x; rank(x)=0; } Always attach smaller tree to larger. union(x, y) { LINK(FIND-Set(x), Find-Set(y)) } LINK(x, y){ if (rank(x) > rank(y)) { p(y) x; else p(x) y; if(rank(x)=rank(y)){ rank(x) = rank(y)+1; } } 34

Union by Weight Heuristic Let’s change the weight from rank to number of nodes: union(x, y) { rep_x = find(x); rep_y = find(y); if (weight[rep_x] < weight[rep_y]) { A[rep_x] = rep_y; weight[rep_y] += weight[rep_x]; } else { A[rep_y] = rep_x; weight[rep_x] += weight[rep_y]; } } 35

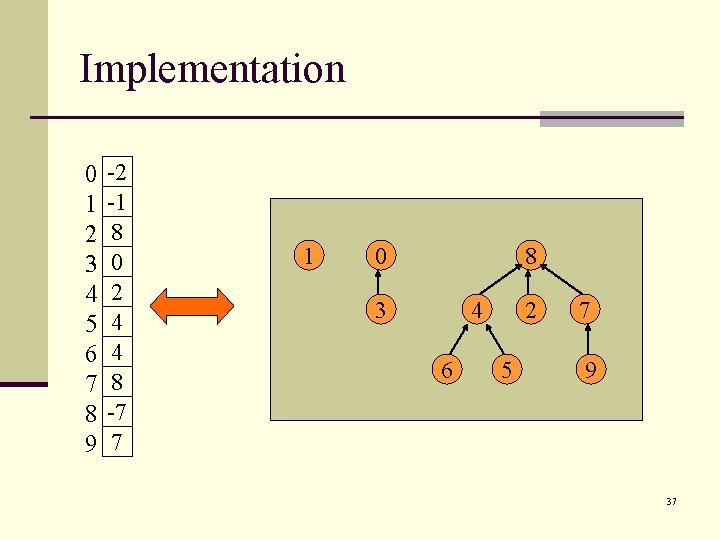
Implementation n Still represent this with an array of n nodes n n If element i is a “root node”, then arr[i]= -s, where s is the size of that set. Otherwise, arr[i] is the index of i’s “parent” n If arr[i] < arr[j], then set arr[i] to arr[i]+arr[j] and set arr[j]to i n Else, set arr[j] to arr[i]+arr[j] and set arr[j] to i 36

Implementation 0 1 2 3 4 5 6 7 8 9 -2 -1 8 0 2 4 4 8 -7 7 1 0 8 3 4 6 2 5 7 9 37

Performance w/ Union by Weight n If unions are done by weight, the depth of any element is never greater than lg N. n n n Initially, every element is at depth zero. When its depth increases as a result of a union operation (it’s in the smaller tree), it is placed in a tree that becomes at least twice as large as before (union of two equal size trees). How often can each union be done? -- lg n times, because after at most lg n unions, the tree will contain all n elements. n Therefore, find becomes O(lg n) when union by weight is used. 38

New Bound on h Theorem: Assume we start with a Union/Find structure where each set has 1 node, and perform a sequence of Weighted Unions. Then any tree T of m nodes has a height no greater than log 2 m. 39

Proof n Base case: If m=1, then this is clearly true n Assumption: Assume it is true for all trees of size m-1 or less n Proof: Let T be a tree of m nodes created by a sequence of Weighted Unions. Consider the last union: Union(Sj, Sk). Assume Sj is the smaller tree. If Sj has a nodes, then Sk has m-a nodes, and 1 a m/2. 40

Proof (continued) n The height of T is either: n n The height of Tk One more than the height of Tj n Since a m-1, the assumptions applies to both Tk and Tj n n If T has the height of Tk, then h log 2(m-a) log 2 m If T is one greater than the height of Tj: h log 2 a +1 log 2 m/2) +1 log 2 m 41

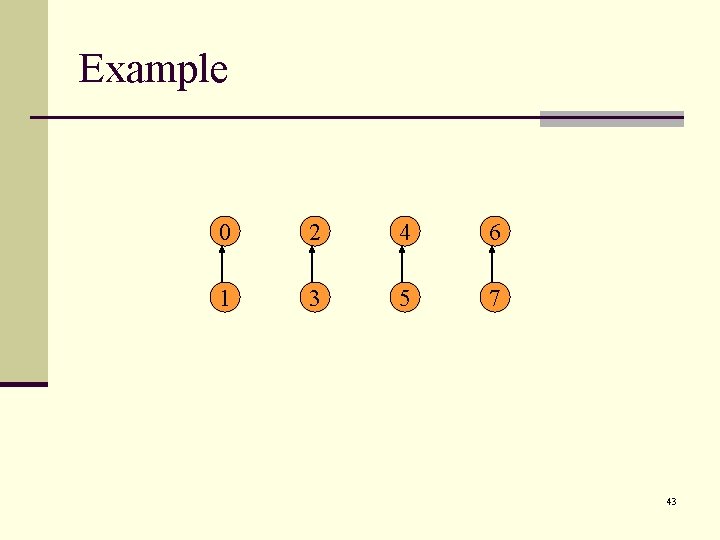
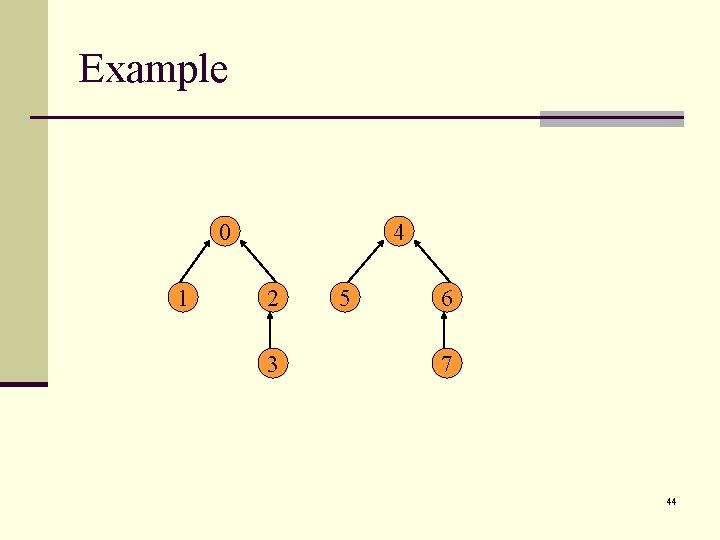
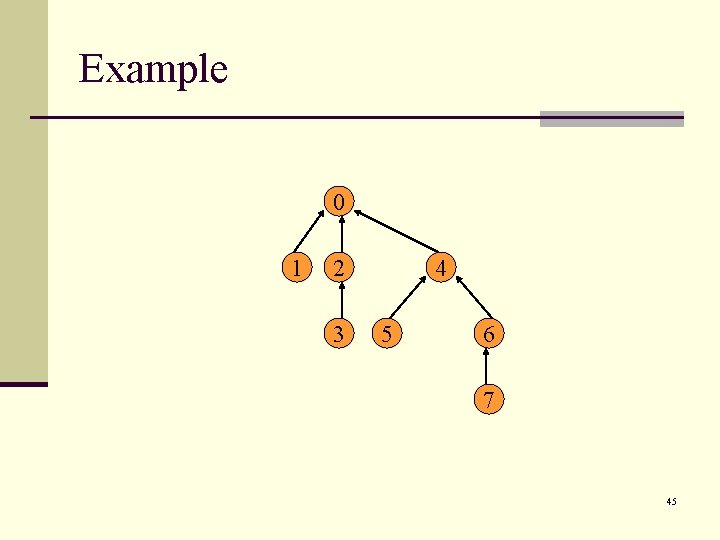
Example Is the bound tight? Yes: “pair them off” Union(S 0, S 1), Union(S 2, S 3), Union(S 4, S 5), Union(S 6, S 7), Union(S 0, S 2), Union(S 4, S 6), Union(S 0, S 4) 0 1 2 3 4 5 6 7 42

Example 0 2 4 6 1 3 5 7 43

Example 0 1 4 2 3 5 6 7 44

Example 0 1 2 3 4 5 6 7 45

Analysis n Worst case: n Union is still O(1) n Find is now O(log n) n Amortized case: n A “worst amortized case” can be achieved if we perform n/2 unions and n/2 finds n Take O(n log n) time n Conclusion: This is better, but we can improve it further 46

Path Compression n Each time we do a find on an element x, we make all elements on path from root to x be immediate children of root by making each element’s parent be the representative. find(x) { if (A[x]<0) return(x); A[x] = find(A[x]); return (A[x]); } n When path compression is done, a sequence of m operations takes O(m lg n) time. Amortized time is O(lg n) per operation. 47

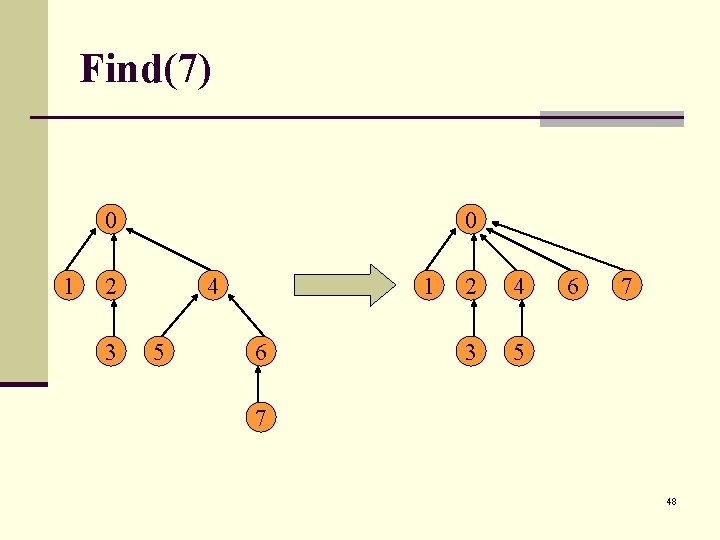
Find(7) 0 1 0 2 3 4 5 1 6 2 4 3 5 6 7 7 48

Analysis n The worst case analysis does not change n In fact, we are going to have to increase the worst-case time of Find by a constant factor n The amortized analysis does get better n we need to define Ackerman’s function 49

Performance with Both Optimizations n When both optimizations are performed, for a sequence of m operations (m n) (unions and finds), it takes no more than O(m lg* n) time. n lg*n is the iterated (base 2) logarithm of n. The number of times you take lg n before n becomes 1. n Example: n lg*16=3 n lg*65536=4 65536=5 n lg*2 n Union-find is essentially O(m) for a sequence of m operations (Amortized O(1)). 50

Ackerman’s Function n Ackerman’s A(i, j) is defined as follows: A(1, j) = 2 j for j 1 A(i, 1) = A(i-1, 2) for i 2 A(i, j) = A(i-1, A(i, j-1)) for i, j 2 n Some values: n n n A(2, 1) = 4 A(2, 2) = 16 A(2, 3) = 65536 A(2, 4) = > 10^100 (probably much greater than this) A(4, 4) = 2^(2^(2^65536)) - 3 51

(p, q) n The function (m, n) is related to the inverse of Ackerman function n For m n 1: (m, n) = min{z 1 | A(z, m/n ) > log 2 n} n This is a very slow growing function: n (m, n) 3 if n < 216 n n has to be huge to make (m, n) = 4 52

Analysis n Lemma (Tarjan and Van Leeuwen): If we start with a Union/Find structure with one element per set (n elements), and let T(f, u) be the time to process any sequence of f finds and u unions. If u n/2 then T(f, u) = (n+ (f+n, n)) n Translation: This is basically linear n In practice, you will never have n large enough to give (f+n, n) a value of even 4 53