Graph Algorithms Mathematical Structures for Computer Science Chapter

Graph Algorithms Mathematical Structures for Computer Science Chapter 6 Copyright Section 6. 1 © 2006 W. H. Freeman & Co. MSCS Slides Directed Graphs and Binary Relations Graph Algorithms

Introduction We confine our attention to (unweighted) directed graphs with no parallel arcs. Two arcs from node a to node b would be parallel, but one arc from a to b and another from b to a are not parallel arcs. The adjacency matrix of the graph is an n n matrix, not necessarily symmetric. The adjacency matrix will be a Boolean matrix, that is, a matrix whose only elements are 0 s and 1 s. There is a one-to-one correspondence between an n n Boolean matrix and the directed graph that the matrix represents. Directed graphs with n nodes, no parallel arcs Section 6. 1 n n Boolean matrices Directed Graphs and Binary Relations 1

Directed Graphs and Binary Relations Section 6. 1 Suppose G is a directed graph with n nodes and no parallel arcs. Let N be the set of nodes. If (ni, nj) is an ordered pair of nodes, then there either is or is not an arc in G from ni to nj. We can use this property to define a binary relation on the set N. This relation is the adjacency relation of the graph. ni nj ↔ there is an arc in G from ni to nj Conversely, if is a binary relation on a set N, we can define a directed graph G with N as the set of nodes, and an arc from ni to nj if and only if ni nj. G will have no parallel arcs. Directed Graphs and Binary Relations 2

Directed Graphs and Binary Relations Section 6. 1 For the directed graph of the figure below, the adjacency relation is {(1, 2), (1, 3), (3, 3), (4, 1), (4, 2), (4, 3)}. For the set N {1, 2, 3, 4} and the binary relation {(1, 4), (2, 3), (2, 4), (4, 1)} on N, we obtain the associated directed graph: Directed Graphs and Binary Relations 3

Directed Graphs and Binary Relations Section 6. 1 We have the following one-to-one correspondences: If function composition is carried out on these bijections, the result is a bijection that gives us a one-to-one correspondence between binary relations and matrices. Recall the reflexive, symmetric, antisymmetric, and transitive properties of a binary relation on a set. If a binary relation on a set N has a certain property, this will be reflected in the corresponding graph and the corresponding Boolean matrix. Directed Graphs and Binary Relations 4

Reachability DEFINITION: REACHABLE NODE In a directed graph, node nj is reachable from node ni if there is a path from ni to nj. The “reachability” property has an interesting interpretation in each of the three equivalent forms in directed graph, adjacency relation, and adjacency matrix. The adjacency matrix A of a directed graph G with n nodes and no parallel arcs will have a 1 in position i, j if there is an arc from ni to nj. Let A(2) be the Boolean matrix multiplication A A given by: Section 6. 1 Directed Graphs and Binary Relations 5

Reachability Section 6. 1 If a term such as ai 2 a 2 j in this sum is 0, then either ai 2 = 0 or a 2 j = 0 (or both), and there is either no path of length 1 from ni to n 2 or no path of length 1 from n 2 to nj (or both). Thus there are no paths of length 2 from ni to nj passing through n 2. A path of length 2 from ni to nj will exist if and only if there is a path of length 2 passing through at least one of the nodes from 1 to n, that is, if and only if at least one of the terms in the sum is 1, A(2)[i, j] = 1. The matrix A(2) indicates the presence or absence of length-2 paths, this result holds for arbitrary powers and path lengths as well. THEOREM ON BOOLEAN ADJACENCY MATRICES AND REACHABILITY: If A is the Boolean adjacency matrix for a directed graph G with n nodes and no parallel arcs, then A(m)[i, j] = 1 if and only if there is a path of length m from node ni to node nj. Directed Graphs and Binary Relations 6

Reachability Section 6. 1 If node nj is reachable from node ni, it is by a path of some length. Such a path will be shown by a 1 as the i, j entry in A or A(2) or A(3)… If there are n nodes in the graph, then any path with n or more arcs (n + 1 or more nodes) must have a repeated node. Therefore, we never need to look for a path from ni to nj of length greater than n. To determine reachability, consult element i, j in A, A(2), . . . , A(n). We can define a reachability matrix R by: R = A A(2), . . . A(n) nj is reachable from ni if and only if entry i, j in R is positive. Directed Graphs and Binary Relations 7

Reachability If is the adjacency relation for a graph G, we let R denote the binary relation of reachability (ni, nj) Î R exactly when there is a path in G from ni to nj. R is the transitive closure of The three equivalent representations of adjacency relation, directed graph G, and adjacency matrix A, correspond to: (ni, nj) belongs to the transitive closure of Section 6. 1 nj reachable from ni in G Directed Graphs and Binary Relations R[i, j] = 1, where R = A A(2) . . . A(n) 8

Reachability Example Given the directed graph, G with 5 nodes: The Adjacency Matrix is: The Boolean Sum of the matrices is: Section 6. 1 Directed Graphs and Binary Relations 9

Reachability Example Section 6. 1 The adjacency relation is = {(1, 2), (2, 3), (3, 1), (3, 4), (5, 1), (5, 3)}. Taking the transitive closure of adds the following pairs: (1, 3), (2, 1), (2, 4), (3, 2), (5, 4), (1, 1), (1, 4), (2, 2), (3, 3). So we have: {(l, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (5, 1), (5, 2), (5, 3), (5, 4)} Notice that it agrees with matrix R. Directed Graphs and Binary Relations 10

Warshall’s Algorithm Section 6. 1 For a graph G with n nodes, Warshall’s algorithm computes a sequence of n + 1 matrices M 0, M 1, M 2, . . . , Mn. For each k, 0 ≤ k ≤ n, Mk[i, j] = 1 if and only if there is a path in G from ni to nj whose interior nodes (i. e. , nodes that are not the endpoints of the path) come only from the set of nodes {n 1, n 2, . . . , nk}. Warshall’s algorithm begins with A = M 0 and M 1, M 2, . . . , Mn = R inductively. The base case is to let M 0 = A. Assume that Mk has been computed, Mk+1[i, j] = 1 if and only if there is a path from ni to nj whose interior nodes come only from the set {n 1, n 2, . . . , nk+1}. Directed Graphs and Binary Relations 11

Warshall’s Algorithm 1. � Section 6. 1 There are two ways to see if Mk+1[i, j] = 1 All the interior nodes come from {n 1, n 2, . . . , nk}, in which case Mk[i, j] = 1. Any 1 entries in Mk are carried forward into Mk+1. Node nk+1 is an interior node. There must be a path from ni to nk+1 whose interior nodes come from {n 1, n 2, . . . , nk} and a path from nk+1 to nj whose interior nodes come from {n 1, n 2, . . . , nk}, so Mk[i, k + 1] = 1 and Mk[k + 1, j] = 1. Directed Graphs and Binary Relations 12

Warshall’s Algorithm Section 6. 1 ALGORITHM Warshall(n n Boolean matrix M) //Initially, M = adjacency matrix of a directed graph G //with no parallel arcs for k = 0 to n - 1 do for i = 1 to n do for j = 1 to n do M[i, j] = M[i, j] (M[i, k + 1] M[k + 1, j ]) end for //at termination, M = reachability matrix of G end. Warshall Directed Graphs and Binary Relations 13

Warshall’s Algorithm 1. 2. 3. Section 6. 1 Informally, Warshall’s algorithm works as follows: Consider column k + 1 in Mk. For each row with a 0 entry in this column, copy that row to Mk+1. For each row with a 1 entry in this column, or that row with row k + 1 and write the resulting row in Mk+1. Directed Graphs and Binary Relations 14

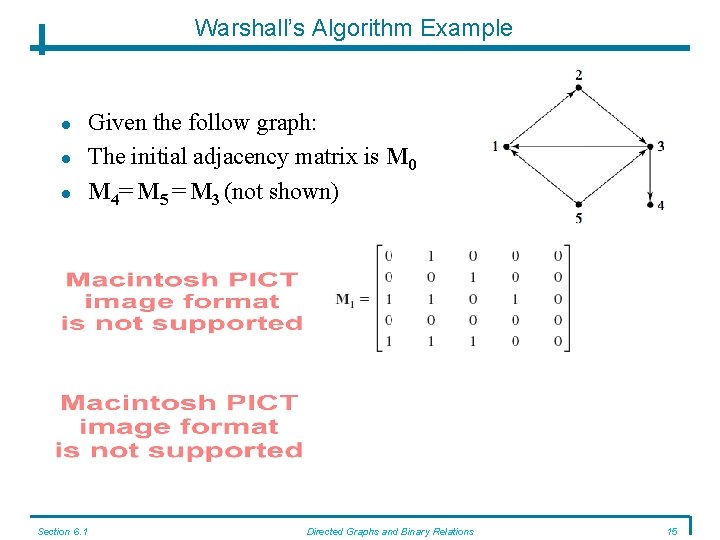
Warshall’s Algorithm Example Section 6. 1 Given the follow graph: The initial adjacency matrix is M 0 M 4= M 5 = M 3 (not shown) Directed Graphs and Binary Relations 15